运筹学在计量技术机构安排企业现场检测中的应用

张大勇

摘要：在为企业提供现场检测服务的过程中，如何科学合理地安排下场计划，运用有限的劳动力资源实现服务方式、经济效益的最大化，成为困扰计量技术机构发展的一大难题。文章运用运筹学原理，以劳动力的供求关系为考虑因素建立模型，对如何安排企业现场检测计划进行分析，以期得到科学合理的下场安排计划。

关键词：运筹学；计量技术机构；企业现场检测；劳动力；供求关系 文献标识码：A

中图分类号：F224 文章编号：1009-2374（2015）13-0050-02 DOI：10.13535/j.cnki.11-4406/n.2015.13.026

随着我国市场经济的发展和入世进程的加快，计量技术机构领域竞争日益激烈，面临着如何转变发展方式，如何适应国际规则与国际接轨的双重压力。不断改进服务方式，增强为企业服务的深度和广度，以便捷化、现场化的服务方式，降低企业运输成本，减少因设备量值溯源形成的经济损失，成为增强企业市场竞争力的一剂良药。然而，计量技术机构也面临着人员紧缺、设备不足等实际问题，如何科学合理地安排下场计划，以有限的人力资源实现服务方式和经济效益的最大化，成为我们不得不面对也不得不思考的问题。本文拟运用运筹学原理，以劳动力的供求关系为考虑因素建立模型，以期得到科学合理的下场安排计划。

计量技术机构在劳动力既定的情况下，安排现场检测主要面临两种情况：一是检测所需劳动力大于实验室已有劳动力；二是检测所需劳动力少于实验室已有劳动力，也即是劳动力的供求问题。当供大于求时，劳动力过剩，既然利润无法提高，我们将主要计算如何将成本降到最低，例如交通费用；当供小于求时，劳动力供不应求，检测工作可有选择性地进行，我们将优先完成利润高的，使经济效益最大化。

1 劳动力过剩情况分析

当供大于求时，应首先考虑将总费用降为最少。这类问题类似于运筹学中经典的运输问题，为便于理解，建模如下：

首先按照每个人工作效率不同将实验室划分为几组，记下每组的劳动力，当成是i个能够提供产品的产地（对应产量）。将不同企业当作j个需要产品的销地（对应销量），记下他们所需要的劳动力。而每一个产地到达每一个销地所需单位运费不同（C）。这里将假定只有运费为需要考虑的支出费用，也即当供大于求时考虑用几个产地的产量来满足所有销地销量，同时保证运费最少的方案。

举一个例子，这里将实验室划分成三组为A1、A2、A3，需要检测的企业共4个，分别设为B1、B2、B3、B4，每组所能提供的劳动力和企业所需劳动力及各地之间单位运费如下表1所示：

表1

明显看出总产量为8+5+9=22，而销量为4+3+5+6=18，产大于销，也就是实验室劳动力剩余。

容易想到，要想运费最省，应该优先考虑单位运价最少部门的供销业务，使其最大限度的满足其销量。即对于所有的i和j，找到，并将的物品量由Am运到Bn。若，则Am的物品全部供应完毕，且Bn所需物品刚好得到满足；若，则Bn需要物品全部得到满足，而Am有剩余；若，则Am物品全部销售完毕，而Bn所需要还没有得到满足，还需要从另外的产地供给。

这里产量大于销量，为了方便计算，可以假想一个销，设为B5，用来存储多余出来的产量。为了不影响总费用计算，可将任意产地到B5的单位运费设为0。这样就不会影响我们计算运费。

根据如上分析，我们可以重新得到如下表格：

表2

首先遍历i和j，得到最小单元运费为从A3到B3的C33=1，这时A3可以完全满足B3，并富余9-5=4，将其在A3行末标出，再将B3划掉。

表3

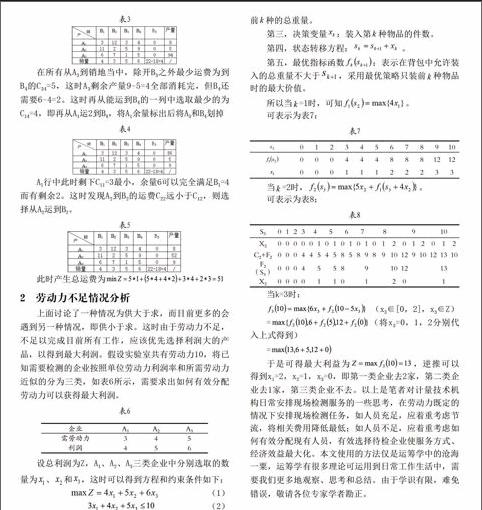
在所有从A3到销地当中，除开B3之外最少运费为到B4的C34=5，这时A3剩余产量9-5=4全部消耗完，但B4还需要6-4=2。这时再从能运到B4的一列中选取最少的为C14=4，即再从A1运2到B4，将A1余量标出后将A3和B4划掉

表4

A1行中此时剩下C11=3最小，余量6可以完全满足B1=4而有剩余2。这时发现A2到B2的运费C22远小于C12，则选择从A2运到B2。

表5

此时产生总运费为

2 劳动力不足情况分析

上面讨论了一种情况为供大于求，而目前更多的会遇到另一种情况，即供小于求。这时由于劳动力不足，不足以完成目前所有工作，应该优先选择利润大的产品，以得到最大利润。假设实验室共有劳动力10，将已知需要检测的企业按照单位劳动力利润率和所需劳动力近似的分为三类，如表6所示，需要求出如何有效分配劳动力可以获得最大利润。

表6

企业 A1 A2 A3

需劳动力 3 4 5

利润 4 5 6

设总利润为Z，A1、A2、A3三类企业中分别选取的数量为、和，这时可以得到方程和约束条件如下：

（1）

（2）

xi≥0且为整数（i=1，2，3） （3）

这又是运筹学中一类典型问题——背包问题。设背包总承重为a，现共有n种物品需要装入包中。第i种物品的重量为ai。这里建模如下，将实验室总利润Z看做背包总承重a，这里将利润最大化也就是将a最大化；上面例子中共有三类企业需要劳动力，类比于有3种物品需要装入包中，每家企业的利润即是每中物品的重量ai

首先定义五个名词，将在下面的分析中用到：

第一，阶段：将可装入物品按照1，2，3…n排序，每阶段装入一种物品，可分为段。

第二，状态变量：阶段开始时，允许装入的前种的总重量。

第三，决策变量：装入第种物品的件数。

第四，状态转移方程：。endprint

第五，最优指标函数：表示在背包中允许装入的总重量不大于，采用最优策略只装前种物品时的最大价值。

所以当=1时，可知。

可表示为表7：

表7

0 1 2 3 4 5 6 7 8 9 10

0 0 0 4 4 4 8 8 8 12 12

0 0 0 1 1 1 2 2 2 3 3

当=2时，。

可表示为表8：

表8

S3 0 1 2 3 4 5 6 7 8 9 10

X2 0 0 0 0 0 1 0 1 0 1 0 1 0 1 2 0 1 2 0 1 2

C2+F2 0 0 0 4 4 5 4 5 8 5 8 9 8 9 10 12 9 10 12 13 10

F2（S3） 0 0 0 4 5 5 8 9 10 12 13

X2 0 0 0 0 1 1 0 1 2 0 1

当k=3时：

（x3∈[0，2]，x3∈Z）

=（将x3=0，1，2分别代入上式得到）

=

于是可得最大利益为，逆推可以得到x1=2，x2=1，x3=0，即第一类企业去2家，第二类企业去1家，第三类企业不去。以上是笔者对计量技术机构日常安排现场检测服务的一些思考，在劳动力既定的情况下安排现场检测任务，如人员充足，应着重考虑节流，将相关费用降低最低；如人员不足，应着重考虑如何有效分配现有人员，有效选择待检企业使服务方式、经济效益最大化。本文使用的方法仅是运筹学中的沧海一粟，运筹学有很多理论可运用到日常工作生活中，需要我们更多地观察、思考和总结。由于学识有限，难免错误，敬请各位专家学者勘正。

参考文献

[1] 滕传琳.论运筹学在我国铁路运输中的应用[J].铁路科技动态，1986，（1）.

[2] 陈御钗.运筹学在连锁企业物流管理中的应用[J].商场管理现代化，2006，（8）.

[3] 薛伟.运筹学在国外木材运输中的应用[J].林业科技，1993，（6）.

[4] 胡运全.运筹学教程（第三版）[M].北京：清华大学出版社，1998.

[5] 孙焕纯.运筹学中若干离散规划问题的相对差分搜索解法[J].运筹与管理，2006，（8）.

[6] 王竹芳.一种求解救灾物资运输问题的解决方法[J].运筹与管理，2012，（2）.

（责任编辑：陈 倩）endprint