基于优化的BPNN模型在色彩空间转换中的应用研究
2015-04-30赵辉艾磊
赵辉 艾磊
摘要摘要:色彩空间转换在图像采集、显示,色彩信息传递及重现中发挥着重要作用,为实现真正意义上的“所见即所得”,需提高色彩转换精度。针对传统色彩空间转换模型中BP神经网络转换精度低、易陷入局部最优等不足,使用萤火虫算法优化BP神经网络的初始权值和阈值,提出一种FABPNN算法的色彩空间转换模型,并使用色差模型进行验证。实验结果表明,该模型具有较高的色彩转换精度,达到预期效果。
关键词关键词:萤火虫算法;色彩空间转换;BP神经网络
DOIDOI:10.11907/rjdk.1431001
中图分类号:TP317.4
文献标识码:A文章编号
文章编号:16727800(2015)004015103
0引言
色彩空间转换是色彩管理中的核心问题,彩色图像恢复或再现过程中出现的颜色失真或改变,受相关设备色彩特性、观测条件(如照明、观测视角、背景等)以及色域范围等因素的影响[1]。为保证图像信息传递的一致性,达到所见即所得的效果,需要通过色彩管理对颜色空间转换进行控制。色彩空间具有跨学科和跨行业的特点,所以诸多色彩空间之间存在相互转换的内在需求[2]。而转换的基本模式是选择一种与设备无关的色彩空间,比如CIELAB或CIEXYZ作为中介,通过RGB、CIELAB/CIEXYZ、CMYK等色彩空间来实现相互转换。
近年来,关于色彩空间转换算法主要有混合色彩模型、回归分析法[3]、多项式法、线性插值法[4]、查表法[5]等。混合模型可以用相对较少的测量数据来预测色彩,但误差分布不均匀,而且应用范围受限。多元回归方法使用较少的样本实现彩色打印机色彩空间转换,不足之处在于转换精度较低。多项式方法的优点是不需要在源空间均匀采样,由于对象空间采样点分布的差异性,多项式回归转换精度也会有很大差异,而且测试时间比较长。查表法主要分为LUT和3DLUT两种,三维查表法主要采用等分分割方法,其变换精度取决于查找表的密度大小,会造成色域的准确性不一致[1]。
在色彩空间转换中,色彩的映射关系并不是简单的对应关系,其变换过程是一种非线性映射[6]。神经网络由于其目标模拟的模糊性、泛化性以及非线性映射与彩色图像信息处理过程的特点相吻合,所以也被应用于色彩转换中。但神经网络存在一些不可避免的缺陷,比如网络结构选择困难,局部极值以及泛化能力差等。而且BP神经网络初始权值和阈值选择不当,将使BP网络难以收敛,从而影响预测效果。萤火虫算法[78](Firefly Algorithm,FA)受自然界中萤火虫通过荧光进行信息交流的群体行为启发演变而来。该算法由剑桥大学的Xin-She Yang教授于2008年提出,是一种新颖的仿生群智能优化算法。本文采用FA优化得到最优初始权值和阈值来构造BP神经网络。在此基础上建立色彩空间转换模型的FABPNN算法。
1BP神经网络模型
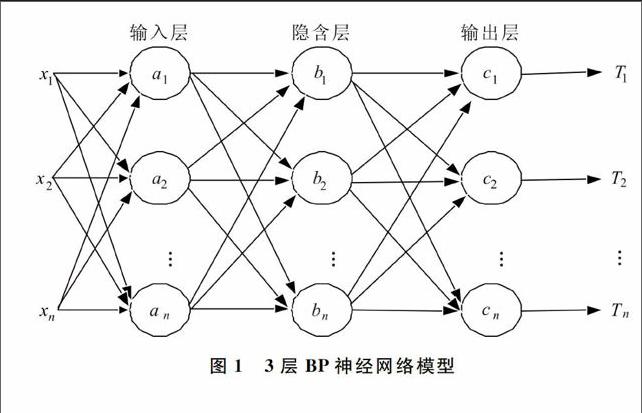
BP神经网络是一种采用误差逆传播(Error Back-Propagation)算法的多阶层前向反馈神经网络,BP是一种有监督的学习算法。标准的BP神经网络分3个部分,即输入向量、隐含层神经元和输出层神经元,如图1所示。输入层单元数等于输入向量分量的个数,隐含层神经元数可按经验通过公式取值,输出层神经元数为期望输出分量。BP神经网络算法基于误差校验学习准则,针对每个独立神经元,寻优过程采用最小均方(LMS)迭代完成,是一个向前计算和误差反向传播,不断修正权值的过程。
2萤火虫算法
2.1萤火虫算法原理
萤火虫算法是通过模拟自然界中萤火虫发光行为构造出的一类随机优化算法,其舍弃了发光的生物学意义,只是利用萤火虫的发光特性来搜索伙伴,并向邻域结构位置较优的萤火虫移动,以此实现位置进化。萤火虫算法需3个理想化的条件:①所有萤火虫无性别差异,任何萤火虫都可能被其它萤火虫吸引;②亮度较暗的萤火虫会被亮度较高的萤火虫吸引,并向它移动,即吸引度和亮度相关;③如果萤火虫周围没有比其更亮的个体,它将随即移动。
其仿生学原理为:用搜索空间中的点模拟萤火虫个体,将搜索和优化过程模拟为萤火虫个体的吸引和移动过程,将问题求解的目标函数度量成个体所处位置优劣,将个体优胜劣汰过程类比成搜索和优化过程中,用好的可行解取代较差的可行解的迭代过程[9]。
2.2相关概念
萤火虫算法主要包含两个要素:亮度和吸引度。亮度体现萤火虫所处位置的优势并决定其移动方向;吸引度决定了萤火虫移动的距离。通过亮度和吸引度不断更新,从而实现目标优化。
3萤火虫算法优化BP网络模型(FABPNN)
3.1萤火虫优化BP网络的色彩转换模型
在BP网络模型的基础上,采用萤火虫算法进行搜索解空间,得到全局最优解来优化神经网络的参数,使网络模型达到较好的拟合效果和泛化能力。
假设:如果目标个体的亮度和个体得到的目标函数解具有关联,那么最优问题可以通过寻找最亮个体得到。BP神经网络中的目标函数,均方差E=1N∑Ni=1(yi-Oi)2,是实际值与网络输出值的均方误差,误差越小越好。在萤火虫算法中,个体的亮度越高,其它个体就会向此个体进行移动,移动的距离主要取决于吸引度的大小。所以采用均方误差函数的倒数作为萤火虫算法中的亮度目标函数。
通过萤火虫算法优化BP神经网络主要在于两点:一是萤火虫当前位置传递给BP网络作为网络的权值和阈值进行计算;二是BP网络的误差作为萤火虫算法的目标函数值进行亮度计算。
FABPNN算法的基本思想:由输入输出参数确定BP的网络结构,从而确定FA算法中个体的编码长度,即BP网络中的所有权值和阈值都是萤火虫个体中的属性;通过目标函数计算萤火虫个体的亮度目标函数值;通过位置更新找到最佳适应度函数对应的个体,将FA优化得到的个体对BP网络的权值和阈值进行赋值,然后训练BP神经网络。基于FABPNN算法的色彩转换模型如图2所示。
3.2FABPNN算法
算法具体步骤如下:
Step1:设置当前迭代次数t=1,确定萤火虫种群数目N,设置最小误差精度和最大迭代次数MaxGeneration,确定BP网络拓扑结构,输入层(I)、隐层(H)、输出层(O)神经元个数,萤火虫个体维度D=I*H+H*O+H+O。随机初始化萤火虫种群位置X=(N,D)。
Step2:将萤火虫的初始位置传递给BP网络,作为BP网络的初始权值和阈值。
Step3:BP神经网络计算。选择神经元激励函数S函数或者线性函数purelin计算BPNN的输出。
f(net)=11+e-net(5)
Step4:计算BP网络的平均误差,并将此误差的倒数返回萤火虫算法作为其目标函数的亮度值。
Step5:如果计算的均方差满足预设精度要求或者达到最大迭代次数,那么记录当前最优萤火虫个体,结束迭代转向Step8,否则转向Step6。
Step6:比较每个萤火虫的亮度大小,亮度低的向亮度高的萤火虫进行移动,达到其空间位置更新。
Step7:迭代次数加1。t=t+1,返回Step3。
Step8:将记录的最优个体赋值给BP神经网络的权值和阈值,进行网络训练。
4模型仿真与验证
4.1数据选取与参数设置
为了验证算法模型的有效性,体现整体色彩空间的变换水平,网络的样本数据采用色彩空间非均匀采样的思想[10],RGB为网络输入值,Lab为输出值。样本的取样间隔为:R,G,B=21,70,117,161,203,238,共有63=216组检验样本。同时,为消除属性差异,对各属性进行无量纲化处理。为保证训练数据的随机性以及算法稳定性,随机选取80%的样本数据作为训练集数据,其余20%作为测试集数据。对于FABPNN色彩转换模型,采用3层BP网络模型,输入层3个神经元(R,G,B),输出层3个神经元(L、a、b)。隐含层神经元设定为10,最大迭代次数为100,萤火虫种群数量为20,种群维度D=73,表示BPNN中的所有权值和阈值,萤火虫算法步长因子为0.2,光强吸收系数为1.0。
4.2色彩精度评价标准及结果分析
色彩评价是利用适当的工具、仪器对样张的各质量特征进行定量监测,然后参照行业标准进行客观评价。色差是色彩评价的最重要参数,它可以评估两色样之间的感觉色彩差距。本文采用CIE色差公式,一般情况下,色差大于6即人眼视觉有明显差异。
5结语
色彩空间转换在色彩管理中起着非常重要的作用,寻找一种更为精确的色彩空间转换模型对再现原始色彩尤为重要。本文针对传统BP网络转换模型因权值和阈值的随机设置,而导致BP网络的预测能力和泛化能力较差等不足,使用群体智能寻优的萤火虫算法对传统的BP神经网络进行了优化改进,提出一种更为精确的色彩空间转换模型。实验结果表明此模型具有较好的色彩转换精度。
参考文献参考文献:
[1]JUAN LI HU,JIA BING DENG.A novel algorithm for color space conversion model from CMYK to LAB[J].Journal of Multimedia ,2010,5(2):159166.
[2]章惠,色彩空间转换的理论和实证研究综述[J].包装工程,2011,32(13):102107.
[3]丁二锐,曾平,刘瑞华,王义峰.基于提升核偏最小二乘回归的色彩校正[J].仪器仪表学报,2008,29(1):7983.
[4]J M KASSON, SL NIN, PlOUFFE JL.Performing color space conversions with threedimensional linear interpolation [J].Electronic Imaging, 1995, 226250.
[5]刘朋瑞,郭炜,付宇卓.基于乘法元的查表法实现的色彩空间转换[J].计算机工程,2007,33(16):251255.
[6]戴仲毅,钱军浩.虚拟大样的BP神经网络模型[J].包装工程,2008,29(3):8486.
[7]YANG XINSHE.Natureinspired metaheuristic algorithms[M].Luniver Press,2008:8396.
[8]YANG XINSHE.Firefly algorithms for multimodal optimization[C].Proc of the 5th International Symposium on Stochastic Algorithms:Foundations and Applications. 2009: 169178.
[9]刘长平,叶春明.一种新颖的仿生群智能优化算法:萤火虫算法[J].计算机应用研究,2011,28(9):32953297.
[10]徐宝卉,李言,薛红.基于色彩管理CRT色彩空间转换方法的研究[J].液晶与显示,2007,28(3):351354.
责任编辑(责任编辑:陈福时)
