基于NoC的众核处理器可靠性仿真分析研究

杨文顶 覃志东

摘 要：随着半导体制造工艺的发展，众核芯片上的晶体管密度不断增加，随之而来的寿命可靠性问题日益严重。为了准确评估芯片的可靠性，本文提出了一种基于蒙特卡洛方法的系统级可靠性仿真框架，并在此基础上研究了NoC通信架构对可靠性的影响。实验结果表明，如果不考虑众核芯片的NoC通信结构，系统级可靠性评估的相对偏差最高可达到60%左右。

关键词：众核处理器；可靠性；蒙特卡洛仿真；片上网络

中图分类号：TP302.7 文献标识码：A 文章编号：2095-2163（2015）02-

An Research on Reliability Simulation of NoC Based Many-core Processors

YANG Wending， QIN Zhidong

（College of Computer Science and Technology， Donghua University， Shanghai 201620 ，China）

Abstract： With the development of semiconductor manufacturing，the transistor density on many-core chips increases relentlessly and causes significant lifetime reliability problem.To estimate the chip reliability accurately，this paper proposes a system reliability simulation framework based on Monte Carlo simulation. In addtion，the network structure is taken into consideration for the system reliability.Experimental results show that the relative deviation of the system-level reliability is up to 60% if the NoC communication structure is discarded .

Keywords： Many-core Processor； Reliability； Monte Carlo Simulation； Network on Chip

0 引 言

众核芯片通过集成多个相对简单的处理器内核，以并行处理的方式达到提升整個处理器计算能力的目的。但当工艺制程达到100nm级以下时，登纳德定律（Dennard Scaling）已失效[1]，即特征尺寸的缩小会使得芯片的功耗密度大幅上升，导致芯片过热，这会加速与芯片温度相关的诸如NBTI、TDDB和EM等物理失效[2]。对于众核芯片，如何进行精确的可靠性分析与评估，并采取切实可行的可靠性设计方法是近年来学术界和产业界研究的热点问题。

目前，在众核可靠性分析与评估方向，已有较多研究成果。文献[3]考虑了芯片的工艺偏差和多种失效机制，综合了威布尔分布、正态分布和高斯分布，提出了一个分层的可靠性分析模型，对比使用蒙特卡洛法来评估可靠性，该模型的计算时间大大缩短，而平均误差只有5%。文献[4]充分挖掘了众核芯片的特点和内核的基本状态，分别建立了基于优雅降级系统和备用冗余系统的可靠性模型，并分析了不同的失效率或冗余内核数量对这两种系统的可靠性的影响，该文献可以帮助芯片设计人员进行可靠性设计空间搜索。文献[5]主要是从内核失效引起的任务迁移的角度，通过迭代不同的任务调度方案来计算系统的可靠性，然后在此基础上实现了基于可靠性感知的优化算法，该方法可以通过较小的代价实现可靠性的较大提升。上述这些文献在进行可靠性评估时，都是把众核芯片简单地等效成处理器内核的集合，实际上，众核芯片广泛采用NoC（Network on chip）通信架构，研究芯片的系统级可靠性，不仅需要考虑内核本身的失效，还要考虑NoC拓扑结构中链路、路由等通信组件造成的影响。

本文在现有文献的研究成果基础上，首先通过众核模拟器GEM5[6]模拟2D-Mesh结构的同构众核平台的运行状况，获取相关数据，然后结合芯片的失效机制，使用蒙特卡洛方法对众核系统级可靠性进行仿真分析，以此来研究NoC通信架构对众核芯片系统级可靠性的影响大小。

1 系统平台模型和失效分析

众核芯片是由大量处理器内核通过互连网络连结而成，内部包含了极为密集而复杂的集成电路，受到芯片上热点（hotspot）的影响，很容易发生失效。集成电路的失效主要包括两类，临时性失效和永久性失效，临时性失效一般是由于外部辐射引起的单粒子翻转（SEU）造成，对芯片本身的可靠性不会造成影响。永久性失效一般是因为电路元件老化引起的，如果芯片内部没有冗余元件，这类型的失效会对系统可靠性造成致命影响，本文只考虑永久性失效。

1.1 基于NoC mesh架构的众核平台

本文针对2D-mesh拓扑结构的NoC众核芯片平台进行研究。如图1（a）所示，m×n个同构内核（PE）通过链路和路由（R）进行互连通信，本文通过GEM5仿真的众核平台上PE为Alpha 21264 处理器核，如图1（b）所示，具体包括了Int Exec、L1Cache、L2Cache等组件，这些组件中任意一个失效都会导致PE失效。

PE通过R链接到NoC上，PE与PE之间的通信，首先要经过R再通过选定的链路进行数据传送，而R是独立的工作器件，芯片温度的升高或通信负载的增大，都会加速其老化甚至失效，而R的失效与PE是相互独立的。

图1 基于2D-mesh拓扑结构的众核芯片

Fig.1 Many-core chip based on 2D-mesh topology structure

1.2 失效机制

无论处理器内核还是NoC通信网络都包含很多集成电路元件，当元件因为温度、电压等因素老化时，芯片就可能发生失效。集成电路元件的失效机制有很多种，在本文的可靠性评估框架中，主要考虑了TDDB、NBTI和EM这3种失效机制，并使用MTTF（Mean Time to Failure）作为可靠性的衡量标准。

1.2.1 TDDB（Time Dependent Dielectric Breakdown）

TDDB效應是指MOS元件和栅极之间的栅极氧化层（SiO2）加上持续时间的电压而被击穿的现象。2002年，Wu等人通过大量实验收集了不同电压和温度下的寿命可靠性数据[7]，建立了TDDB相关的系统MTTF的数学模型，如式（1）所示：

（1）

其中，VGS为门电压，T为开氏温度，α、β、X和Y为拟合参数，K为玻尔兹曼常数，AG为栅极表面积，ATDDB为经验常数。从公式（1）可以看出，随着温度的升高，电路的平均失效时间以大于指数级的速率在下降。为了方便实验，本文使用了参考文献[2]中具体参数值： α=78，β=-0.081，X=0.759 eV，Y=-66.8 eVK，Z=-8.37E-4 eV/K。

1.2.2 NBTI（Negative-bias Temperature Instability）

NBTI效应指的是在较高的负栅极电压和温度下PMOS管发生阈值电压的负向漂移，导致元件迁移率下降，从而引发元件失效。文献[8]的研究表明，NBTI相关的寿命可靠性很大程度上依赖于元件本身的温度，其平均失效时间的数学模型用式（2）表示：

（2）

上式中，A、B、C和D都为拟合参数，K为玻尔兹曼常数， A=1.6328，B=0.07377，C=0.01，D=-0.06852，β=0.3 。

1.2.3 EM（Electromigration）

EM是指电路中电子流动导致的金属原子迁移的现象，该现象会导致集成电路内部发生断路或短路，从而引发芯片失效。根据文献[9]，EM效应对系统MTTF的影响可用下式表示：

（3）

上式中，Ea为电子迁移的激活能，T为开氏温度，K为玻尔兹曼常数，J为电流密度，J = 1.5 × 106A/cm2，n=2，Ea = 0.48eV。

2 基于蒙特卡洛方法的系统级可靠性仿真

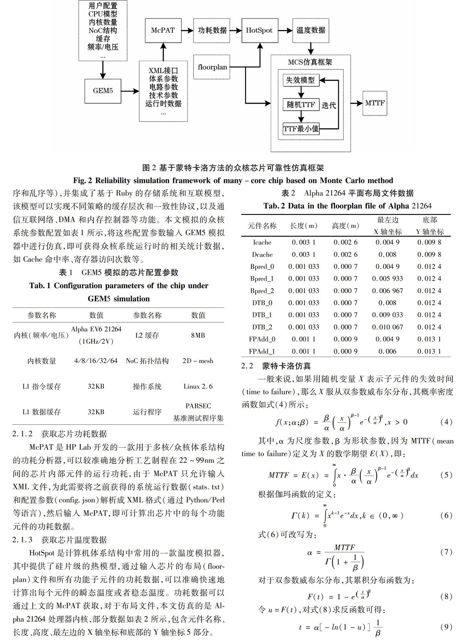
为了准确模拟众核芯片的实际运行情况，本文采用了GEM5全系统模拟器，通过输入具体的芯片参数，获得运行阶段的系统统计数据，然后挂载功耗模拟器McPAT[10]以获得相应的功耗数据，将这些数据输入HotSpot[11]温度模拟器即可计算出每个子元件的具体温度。最后将温度和芯片布局输入到蒙特卡洛仿真器中计算系统级的MTTF，整个可靠性仿真框架如图2所示。

图2 基于蒙特卡洛方法的众核芯片可靠性仿真框架

Fig.2 Reliability simulation framework of many-core chip based on Monte Carlo method

2.1 众核平台模拟与参数获取

2.1.1获取芯片运行数据

GEM5是一个离散事件驱动的模块化计算机体系模拟器，可以方便地重构、参数化、扩展和替换 GEM5 的组件来模拟不同的计算机系统。GEM5不仅支持ALPHA、ARM、X86和SPARC等多种指令集架构，同时也支持多种CPU模型（顺序和乱序等），并集成了基于Ruby的存储系统和互联模型，该模型可以实现不同策略的缓存层次和一致性协议，以及通信互联网络、DMA和内存控制器等功能。本文模拟的众核系统参数配置如表1所示，将这些配置参数输入GEM5模拟器中进行仿真，即可获得众核系统运行时的相关统计数据，如Cache命中率、寄存器访问次数等。

表1 GEM5模拟的芯片配置参数

Tab.1 Configuration parameters of the chip under GEM5 simulation

参数名称

数值

参数名称

数值

内核（频率/电压）

内核数量

L1指令缓存

L1数据缓存

Alpha EV6 21264（1GHz/2V）

4/8/16/32/64

32KB

32KB

L2缓存

NoC拓扑结构

操作系统

运行程序

8MB

2D-mesh

Linux 2.6

PARSEC基准测试程序集

2.1.2获取芯片功耗数据

McPAT是HP Lab开发的一款用于多核/众核体系结构的功耗分析器，可以较准确地分析工艺制程在22～99nm之间的芯片内部元件的运行功耗，由于McPAT只允许输入XML文件，为此需要将之前获得的系统运行数据（stats.txt）和配置参数（config.json）解析成XML格式（通过Python/Perl等语言），然后输入McPAT，即可计算出芯片中的每个功能元件的功耗数据。

2.1.3 获取芯片温度数据

HotSpot是计算机体系结构中常用的一款温度模拟器，其中提供了硅片级的热模型，通过输入芯片的布局（floorplan）文件和所有功能子元件的功耗数据，可以准确快速地计算出每个元件的瞬态温度或者稳态温度。功耗数据可以通过上文的McPAT获取，对于布局文件，本文仿真的是Alpha 21264处理器内核，部分数据如表2所示，包含元件名称、长度、高度、最左边的X轴坐标和底部的Y轴坐标5部分。

表2 Alpha 21264平面布局文件数据

Tab.2 Data in the floorplan file of Alpha 21264

元件名称

长度（m）

高度（m）

最左边X轴坐标

底部Y轴坐标

Icache

Dcache

Bpred_0

Bpred_1

Bpred_2

DTB_0

DTB_1

DTB_2

FPAdd_0

FPAdd_1

0.0031

0.0031

0.001033

0.001033

0.001033

0.001033

0.001033

0.001033

0.0011

0.0011

0.0026

0.0026

0.0007

0.0007

0.0007

0.0007

0.0007

0.0007

0.0009

0.0009

0.0049

0.008

0.0049

0.005933

0.006967

0.008

0.009033

0.010067

0.0049

0.006

0.0098

0.0098

0.0124

0.0124

0.0124

0.0124

0.0124

0.0124

0.0131

0.0131

2.2 蒙特卡洛仿真

一般来说，如果用随机变量X表示子元件的失效时间（time to failure），那么X服从双参数威布尔分布，其概率密度函数如式（4）所示：

（4）

其中α为尺度参数，β为形状参数，因为MTTF（mean time to failure）定义为X的数学期望E（X），即：

（5）

根据伽玛函数的定义：

（6）

式（6）可改写为：

（7）

对于双参数威布尔分布，其累积分布函数为：

（8）

令u=F（t），对式（8）求反函数可得：

（9）

由于上文已获得芯片中子元件的温度，在不同失效机制下，尺度参数α可以通过式（7）计算，如果不考虑工艺偏差，形状参数β则为常数（如β=1.6），因此根据式（9），只需在（0，1）区间内随机生成失效概率u，可得到一个元件随机的ttf（time to failure）。本文假设芯片中没有冗余元件，一个元件失效即代表整个芯片失效，那么在一次迭代中，所有元件的ttf最小值即为芯片系统级的ttf，迭代N次后取平均值，就可得到系统的平均失效时间，本文所实现的蒙特卡洛仿真算法如下所示。

算法1 基于蒙特卡洛仿真的可靠性评估算法

输入：失效机制种类数M，迭代次数N，元件数量K，芯片布局和温度

输出：系统平均失效时间

1. for i ←1 to M do

2. for j ← 1 to N do

3. ttfmin ← ∞

4. for k ← 1 to K do

5. ttfk ← generate_random_ttf（i）

6. if ttfk < ttfmin then

7. ttfmin = ttfk

8. end if

9. end for

10. mttfi += ttfmin / N

11. end for

12. end for

13. return min{mttfi}

3 实验研究

本文使用的實验主机为Intel 酷睿2双核 E7400，内存2GB，操作系统为Ubuntu 14.04 LTS 64位，主要程序代码使用C语言编写。GEM5全系统中模拟的众核芯片内核为Alpha 21264，内核上运行的操作系统为linux 2.6，运行的软件任务为基准测试程序集PARSEC[12]。针对考虑NoC和不考虑NoC两种情况，运行一段时间后，通过GEM5输出的统计数据分析每个元件的温度，然后输入蒙特卡洛可靠性评估框架计算可靠性。需要注意的是，上文提到的失效模型基于比例产生，具体的比例参数是未知的，所以实验中假设面积为1mm2的元件在标准温度（300K）下的MTTF为30，根据这个设定来标准化系统的可靠性。

3.1 不同失效机制

在本次实验中，研究使用了GEM5模拟了4×4 的16核芯片，并仿真了在TDDB、NBTI和EM这三种不同失效机制下的芯片可靠性，结果如表3所示。由于蒙特卡洛仿真的收敛速度与N1/2成正比，随着迭代次数增加，蒙特卡洛仿真估计出的系统MTTF精度不断提高，实验中可以发现，当迭代次数达到105次时，蒙特卡洛方法仿真的系统级MTTF的精度已较高，继续增加迭代次数几乎不改变现有结果，所以本文实验中迭代次数都设置为105次。根据表3的结果，三种失效机制相比，TDDB效应对芯片可靠性的影响相对更大，失效机制越多，系统的可靠性越低。同时，对比考虑NoC和不考虑NoC两种情形，系统级可靠性的相对偏差约为60%左右。

表3 不同失效機制下芯片可靠性试验结果

Tab.3 Experimental results of the chip reliability with different failure mechanisms

失效模型

标准化MTTF（不考虑NoC）

标准化MTTF（考虑NoC）

相对偏差（%）

NBTI

TDDB

EM

NBTI+TDDB+EM

4.1706

0.4259

2.7612

0.4086

1.6099

0.1718

1.0774

0.1642

61.40

59.65

60.98

59.82

3.2 不同内核数量

在接下来的实验中，研究分别对4核、8核、16核和32核的众核芯片进行了模拟，芯片运行的应用程序都是PARSEC中的Blackscholes程序，并且都综合了NBTI、TDDB和EM三种失效机制，结果如表4所示，可以看出，随着内核数量增加，芯片的可靠性下降幅度较大，对比考虑NoC和不考虑NoC两种情形，系统级可靠性的相对偏差依然是60%左右。

表4 不同内核数量时芯片可靠性试验结果

Tab.4 Experimental results of the chip reliability with different cores number

内核数量

标准化MTTF（不考虑NoC）

标准化MTTF（考虑NoC）

相对偏差（%）

4 （2×2）

8 （2×4）

16 （4×4）

32 （4×8）

0.9574

0.6245

0.4086

0.2676

0.3836

0.2503

0.1642

0.1073

59.93

59.92

59.82

59.91

3.3 不同基准测试程序

为了分析不同软件任务下的平均失效时间，本文运行了Blackscholes、Canneal、Streamcluster和Swaptions这4个不同的基准测试程序。由于这些基准测试程序运行都包括3个阶段，初始阶段、并行计算阶段和结束阶段，为了便于采样，实验中研究使用了检查点（checkpoint）技术，从并行计算部分开始执行。在这一部分的实验中，同样研究了NoC结构对系统可靠性的影响，如图3所示，无论是4、16和64核系统上运行基准测试程序，如果不考虑NoC，系统平均失效时间相对考虑NoC的情况相对偏差约为10%-60%，

图3 不同基准测试程序下芯片可靠性试验结果

Fig.3 Experimental results of the chip reliability on different benchmarks

4 结束语

本文使用蒙特卡洛方法对众核芯片的系统级可靠性进行仿真分析，并重点研究了NoC通信架构对可靠性评估的影响，实验结果表明，无论是在不同内核数量、不同失效机制还是不同软件任务下，如果不考虑NoC通信架构，系统级可靠性评估的相对偏差最高都可达60%左右，该结果对以可靠性分析为基础的可靠性优化设计造成较大影响。

参考文献：

[1] ESMAEILZADEH H， BLEM E， AMANT R S， et al. Power challenges may end the multicore era[J]. Communications of the ACM， 2013， 56（2）： 93-102.

[2] SRINIVASAN J. Lifetime reliability aware microprocessors[D]. Urbana-Champaign： University of Illinois ， 2006.

[3] XIANG Y， CHANTEM T， DICK R P， et al. System-level reliability modeling for MPSoCs[C]//Proceedings of the eighth IEEE/ACM/IFIP international conference on Hardware/software codesign and system synthesis. ACM，2010： 297-306.

[4] HUANG L， XU Q. On modeling the lifetime reliability of homogeneous manycore systems[C]//Dependable Computing， 2008. PRDC'08. 14th IEEE Pacific Rim International Symposium on. Taipei：IEEE， 2008： 87-94.

[5] GU Z， ZHU C， SHANG L， et al. Application-specific MPSoC reliability optimization[J]. Very Large Scale

Integration （VLSI） Systems， IEEE Transactions on， 2008， 16（5）： 603-608.

[6] BINKERT N， BECKMANN B， BLACK G， et al. The gem5 simulator[J]. ACM SIGARCH Computer Architecture News， 2011， 39（2）： 1-7.

[7] WU E， SUNE J， LAI W， et al. Interplay of voltage and temperature acceleration of oxide breakdown for ultra-thin gate oxides[J]. Solid-State Electronics， 2002， 46（11）： 1787-1798.

[8] ZAFAR S， LEE B H， STATHIS J， et al. A model for negative bias temperature instability （NBTI） in oxide and high κpFETs 13×-C6D8C7F5F2[C]//VLSI Technology， 2004. Digest of Technical Papers. 2004 Symposium on， Honolulu， HI， USA：IEEE， 2004： 208-209.

[9] HUANG L， YUAN F， XU Q. Lifetime reliability-aware task allocation and scheduling for MPSoC platforms[C]//Proceedings of the Conference on Design， Automation and Test in Europe，Nice， France：European Design and Automation Association， 2009： 51-56.

[10] LI S， AHN J H， STRONG R D， et al. McPAT： an integrated power， area， and timing modeling framework for multicore and manycore architectures[C]//Microarchitecture， 2009. MICRO-42. 42nd Annual IEEE/ACM International Symposium on. New York，USA：IEEE， 2009： 469-480.

[11] SKADRON K， STAN M R， HUANGW， et al. Temperature-Aware Microarchitecture[C]//Proceedings of the 30th International Symposium on Computer Architecture， San Diego，CA，USA：ISCA，June 2003.

[12] Bienia C， Li K. Benchmarking modern multiprocessors[M]. USA： Princeton University，2011.

基金项目：中央高校基本科研業务费专项基金（11D11209）。

作者简介：杨文顶（1988-），男，安徽合肥人，硕士生，主要研究方向：多核/众核可靠性设计；

覃志东（1974-），男，四川广汉人，博士，副教授，主要研究方向：嵌入式与可编程系统。