基于有限元方法的高速铁路H型钢柱模态分析
2015-04-29杨建
杨建
1.概述
随着高速铁路高速发展,在高铁建设中,H型钢柱因其优异的结构特性,被广泛使用在供电接触网架设中。有限元分析方法是有限元法的基本思想,是在力学模型上将一个原来连续的物体离散成为有限个具有一定大小的单元,这些单元仅在有限个节点上相连,并在节点上引进等效力以替代实际作用于单元的外力。对于每个单元,根据分块近似的思想,选择一种简单的函数来表示单元内位移的分布规律,建立单元节点力和节点位移之间的关系。最后把所有单元的这种关系式集合起来,就得到一组以节点位移为未知量的代数方程,解这些方程就可以求出物体上的有限个离散点上的位移。模态分析是根据用结构的固有特征,包括频率、阻尼和模态振型,这些动力学属性去描述结构的过程。面对大量使用的H型钢柱,利用有限元分析方法,对模态进行分析,可以获得H型钢柱的结构特性,以便更好的应用于高铁接触网建设。
2.有限元方法分析
2.1 利用三维制图软件,按照 H型钢柱型号参数,按如下参数建立三维模型。H型钢柱制造规格、长度应满足接触网安装尺寸及荷载方面的要求。制造H型钢柱的柱身材料必须为热轧H型钢,其尺寸、外形、参考重量及静态参数应满足德国标准DIN1025-2与DIN1025-4。此次分析以GHT240A/7.4 型号的H型钢柱为模型。
型号:GH240A 对应图纸:通化(2008)1301
h(mm ):240 b(mm):240
t1(mm):10 t2(mm):17
r(mm):21
2.2 三维模型图
质量:1580.05 lb 体积:5557.27 in^3密度:0.284322 lb/in^3 重量:1578.98 lbf
2.3 分析步骤
2.3.1 定义材料属性
H型钢柱的钢材采用Q235B
名称:Q235B钢,热轧条材 模型类型: 线性弹性同向性
屈服强度: 1.8e+008 N/m^2 張力强度: 3.25e+008 N/m^2
质量密度: 7870 kg/m^3 弹性模量: 2e+011 N/m^2
泊松比:0.29 热扩张系数: 1.22e-005 /Kelvin
2.3.2 施加约束条件及载荷
为简化分析模型,忽略接触网对钢柱的影响,只对H型钢柱底盘法兰施加固定约束,使H型钢柱固定。
2.3.3 网格化三维模型
网格类型: 实体网格 所用网格器:基于曲率的网格
最大单元大小:134.217 mm 最小单元大小:26.8435 mm
雅可比点:4 点 网格品:质高
2.3.4 运算
对建立的有限元模型,利用计算机图形仿真单元进行计算。
3.模拟结果
4.结果分析
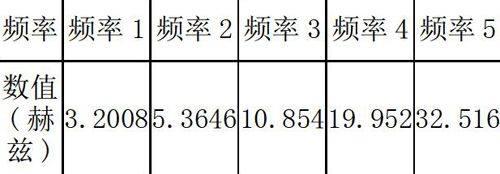
4.1 模拟分析后,得出该型号H型钢柱的共振频率如下:
频率
频率1
频率2
频率3
频率4
频率5
数值(赫兹)
3.2008
5.3646
10.854
19.952
32.516
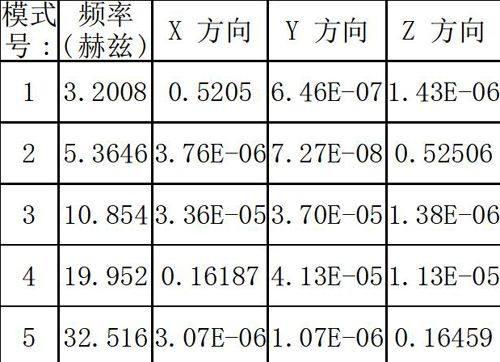
4.2 质量参与
模式号:
频率 (赫兹)
X 方向
Y 方向
Z 方向
1
3.2008
0.5205
6.46E-07
1.43E-06
2
5.3646
3.76E-06
7.27E-08
0.52506
3
10.854
3.36E-05
3.70E-05
1.38E-06
4
19.952
0.16187
4.13E-05
1.13E-05
5
32.516
3.07E-06
1.07E-06
0.16459
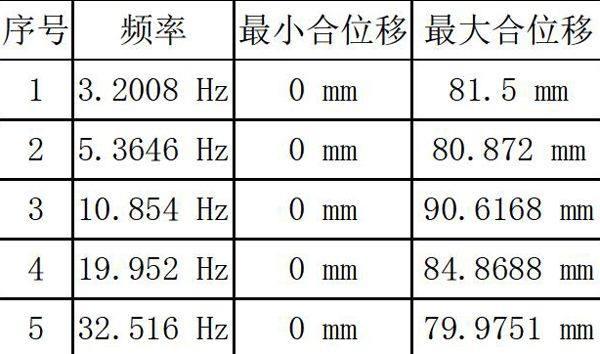
4.3 结果比较
序号
频率
最小合位移
最大合位移
1
3.2008 Hz
0 mm
81.5 mm
2
5.3646 Hz
0 mm
80.872 mm
3
10.854 Hz
0 mm
90.6168 mm
4
19.952 Hz
0 mm
84.8688 mm
5
32.516 Hz
0 mm
79.9751 mm
5.H型钢柱模态分析的意义
模态分析的最终目标在是识别出系统的模态参数,为结构系统的振动特性分析、振动故障诊断和预报以及结构动力特性的优化设计提供依据。模态分析技术的应用可归结为一下几个方面:
(1)评价现有结构系统的动态特性;
(2)在新产品设计中进行结构动态特性的预估和优化设计;
(3)诊断及预报结构系统的故障;
(4)识别结构系统的载荷。
6.结论
利用有限元方法的高速铁路H型钢柱的优势,能够对模型试验条件所产生的误差进行仿真分析,H型钢柱结构也具有固有频率和模态振型,这些特性取决于确定结构固有频率和模态振型的结构质量和刚度分布。本文应用计算机三维制图建立数学模型,通過有限元理论,建立了H型钢柱的有限元模型,通过模型的模态分析,得到了模型的5个谐振频率,以及各频率下该型号H钢柱在谐振频率下的最大和位移,对研究H型钢柱结构的固有特性,理解固有频率和模态振型,有助于设计H型钢柱更优的结构。
参考文献:
[1]《有限元分析:ANSYS理论与应用》
[2]于万聚.高速电气化铁路接触网.成都:西南交通大学出版社,2003.
[3]曾攀.有限元分析基础教程(ANSYS算例).清华大学,2008.
