0—1整数规划最优模型在物品设计中的应用

汤志浩

摘 要： 以储药柜的设计为例介绍了0-1整数规划数学模型在物品设计方面的应用。药房内的盒装药品种类繁多，药盒尺寸规格差异较大，一般的储药柜为横纵向等距的设计方案，药盒与两侧竖向隔板之间的间隙会造成宽度冗余，药盒与上面隔板的间隙会造成高度冗余。增加竖向隔板的间距类型数量可以有效地减少宽度冗余，但会增加储药柜的加工成本，同时降低了储药槽的适用范围。研究确定储药柜横纵向隔板间距的类型数量，使得储药柜的总平面冗余量尽可能地小，对现实中储药柜的设计具有重要的指导意义。

关键词： 0-1矩阵； 0-1整数规划； 隔板间距类型； 冗余

中图分类号： O 29 文献标志码： A 文章编号： 1671-2153（2015）03-0073-05

1 问题提出

储药柜的结构类似于书橱，通常由若干个横向隔板和竖向隔板将储药柜分割成若干个储药槽。为保证药品分拣的准确率，防止发药错误，一个储药槽内只能摆放同一种药品。药品在储药槽中从后端放入，从前端取出。为保证药品在储药槽内顺利出入，要求药盒与两侧竖向隔板之间、与上面横向隔板之间应留2 mm的间隙，同时还要求药盒在储药槽内推送过程中不会出现并排重叠、侧翻或水平旋转。利用某医院现有药盒的规格数据，要求设计时希望总高度、宽度冗余尽可能小，同时也希望间距的类型数量尽可能少，给出合理的横竖向隔板间距类型的数量以及每种类型对应的药品编号。对于这类问题的研究一般都会考虑同样的约束条件（不能侧翻、并排重叠、水平旋转等），然后对每一种规格（本文共有1919种规格）的药盒建立优化模型进行求解。最后在Excel表格中进行排序求得结果。本文是对所有规格的药盒按照宽、高建立0-1整数规划模型，考虑同样的约束条件，利用LINGO软件求得冗余最小、间距类型最少的最优解，最后再综合将长宽高三方面综合考虑，并计算出最终需要的储药柜的个数，这样无论有多少种规格只要将数据带入模型再利用数学软件都可以得到最优解，而不是对每一种规格都要建立最优模型。该模型具有一定的普适性，对于庞大的数据只需导入数学软件就可以快速的计算出答案，方便快捷。

2 模型建立

模型假设：（1）一个储药槽内只能摆放同一种药品；（2）上下两层横向隔板之间应留2 mm的间隙；（3）忽略横向和竖向隔板厚度。

2.1 模型一

本部分依据某医院现有药盒的规格数据建立模型，给出竖向隔板间距类型最少的储药柜设计方案。

药房内的盒装药品种类繁多，药盒尺寸规格差异较大，某医院现有药盒的规格有1919种，其中按宽度又可以分为47种[1]。为保证药品在储药槽内顺利出入，要求药盒与两侧竖向隔板之间、与上下两层横向隔板之间应留2 mm的间隙，同时还要求药盒在储药槽内推送过程中不会出现并排重叠、侧翻或水平旋转。在忽略横向和竖向隔板厚度的情况下，建立如下数学模型：

先建立一个行i=1，2，…，1919，共有1919个，列j=12，13，…，58总共有47个的0-1矩阵[2]，即：

x1，12 x1，13 … x1，58x2，12 x2，13 … x2，58 … … … …x1919，12 x1919，13 … x1919，58。

该矩阵中，xij只能取0和1（xij取1表示编号为i的药盒取到编号为j的药槽，0表示没取到）。行标i是选取的药品的种类，从1取到1919表示共有1919种药品；列标j是根据药盒的宽度的最大值56和最小值10，在考虑了2 mm的间隙的情况下选取的从12取到58。列标12表示最小宽度为10 mm再增加2 mm宽度冗余，列标13表示宽度为11 mm再增加2 mm宽度冗余， 列标58表示最大宽度为56 mm再增加2 mm宽度冗余，其余下标以此类推，其中每一行的所有元素相加之和为1，例如x1j=1表示编号为1的药品只能选1种槽。

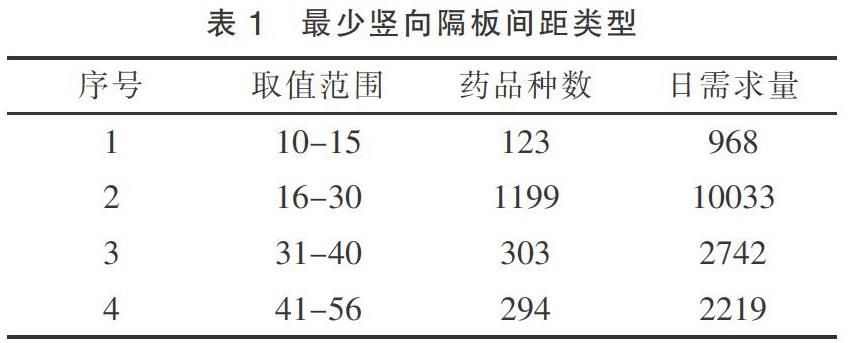
上述数学模型可以放在LINGO软件[3]中求解，要求竖向隔板间距类型最少，即要求：竖向隔板之间的距离尺寸值的大小、隔板间距越相同越接近则越好。因此，可以得到的每个层次的宽度取值范围（如表1所示），则为本问中的所需求宽度的答案。由表1可以看出，在表格中选取范围时，也容易看出类型的数量和每种类型所对应的药盒规格。

本模型以纵向隔板间距类型最少为目标函数，在考虑了药盒在储药槽内推送过程中不会出现并排重叠、侧翻或水平旋转，并以这几条为约束条件，建立了0-1线性规划模型一，该模型符合实际，充分利用了数学软件LINGO将庞大的数据代入模型进行处理，求得结果，所得的结果误差较小、结果准确合理、切实可行，较好的解决了一般的储药柜为横纵向等距的设计方案，使得药盒与两侧竖向隔板之间的间隙会造成了很大的宽度冗余的问题，模型实用性强，对现实有较强的指导意义。

2.2 模型二

本部分建立模型给出合理的竖向隔板间距类型的数量以及每种类型对应的药品编号。

仍利用某医院现有药盒的规格数据，要求设计时希望总宽度冗余尽可能小，同时也希望间距的类型数量尽可能少，给出合理的竖向隔板间距类型的数量以及每种类型对应的药品编号。

在模型一中，已得出竖板间距槽道类型最少的方案：冗余最小时，即每种宽度尺寸设计一种槽道，此法的制作成本最大，故而不可取。

假设第一层次槽宽冗余为Q1，则Q1=l1x1j-b1-2，第一层次药盒宽度范围为[10，q1]，q1表示第一层次药盒宽度范围的上届。

模型二中有两个目标函数：z1为间距类型，要达到最少；z2为槽宽总冗余值，要最小。因为在第一部分中只分了4种层次，第一层次药盒的范围为[10，15]。为了减小冗余，药盒宽度范围应该分的更细，故得到q1的范围为10到15之间，在第一部分得到的槽宽为药盒最大值加上2 mm即17 mm，故Q应在12到17之间，其他字母同模型一中的说明。

这里可以借用数学软件LINGO求得最优解。可得出Q1和q1在z2最小值时的大小。这时可以达到第一个层次区间药盒的宽度范围。各层次宽度取值范围为

[10，q1]，[q1+1，q2]，.....，

此次药槽分的更细，从而有效地减小了冗余。表2为考虑了冗余的纵向隔板规格。表2中，这9种情况下，利用软件计算出来的最小冗余为2651 mm[5]。

本模型主要针对药盒的宽度，在模型一的基础上建立了两个目标函数，除了以纵向隔板间距类型最少为目标函数，还要求槽宽总冗余值最小，并以其为第二个目标函数，两个同时考虑，再考虑药盒在储药槽内推送过程中不会出现并排重叠、侧翻或水平旋转，并以这几条为约束条件，建立了0-1线性规划模型二，该模型主要解决储药槽的纵向隔板设计，以及宽度冗余，符合实际，充分利用了数学软件LINGO对于大数据处理和解决复杂数学问题方便快捷的优势，所得的结果误差较小，结果准确合理，较好的解决了一般的储药柜为横纵向等距的设计方案。

2.3 模型三

为了补药的便利性，储药柜的宽度不超过2.5 m，高度不超过2 m，传送装置占用的高度为0.5 m，即储药柜的最大允许有效高度为1.5 m。药盒与上层横向隔板之间的间隙超出2 mm的部分可视为高度冗余，平面冗余=高度冗余×宽度冗余。要求在第二部分计算结果的基础上，确定储药柜横向隔板间距的类型数量，使得储药柜的总平面冗余量尽可能地小，且横向隔板间距的类型数量也尽可能少。

再次建立一个行i=1，2，…，1919，共有1919个，列j=30，31，…，127总共有98个的0-1矩阵，即：

y1，30 y1，31 … y1，127y2，30 y2，31 … y2，127 … … … …y1919，30 y1919，31 … y1919，127。

该矩阵中，yij只能取0和1（yij取1表示编号为i的药盒取到编号为j的药槽，0表示没取到）。行标i是选取的药品的种类，从1取到1919表示共有1919种药品，列标j是根据药盒的高度的最大值125和最小值28，在考虑了2 mm的间隙的情况下选取的从30取到127。列标30表示最小高度为28 mm再增加2 mm高度冗余，列标31表示高度为29 mm再增加2 mm高度冗余， 列标127表示最大高度为125 mm再增加2 mm高度冗余，其余以此类推，其中每一行的所有元素相加之和为1，例如y1j=1表示编号1的药品只能选1种槽。

本模型主要针对药盒的高度，在前两个模型的基础上建立了两个目标函数：一是横向隔板间距类型最少，二是槽高总冗余最小。以这两个量为目标函数同时考虑，再考虑药盒在储药槽内推送过程中不会出现并排重叠、侧翻或水平旋转，并以这几条为约束条件，建立了0-1线性规划模型三。该模型主要解决储药槽的横向隔板设计，以及高度冗余，符合实际，充分利用了数学软件LINGO解决复杂数学问题的优势，所得的结果误差较小，结果准确合理，建立的模型原理简单，切实可行，较好的解决了一般的储药柜不考虑药盒实际，横纵向等距的设计，造成药盒与上面横向隔板之间很大的高度冗余。

2.4 模型四

结合每一种药品编号对应的最大日需求量数据，在储药槽的长度为1.5 m，每天仅集中补药一次的情况下，计算每一种药品需要的储药槽个数。为保证药房储药满足需求，根据前面模型中单个储药柜的规格，计算最少需要的储药柜个数。

设每一种药品编号对应的最大日需求量ni，结合每个药盒的长度ai，建立模型四[6]可以计算出每一种药品需要的储药槽个数mi，和最少需要的储药柜个数z5。

模型四：

结合模型二三的计算结果，可以知道药槽的最佳规格为20×9=180（种），每种槽道的总药盒数设为Ai（i=1，2，…，180），满足1天药品采集所需要的槽道数量为Bi（i=1，2…，180），每种药槽的所有药盒总长设为Ci（i=1，2，…，180），最小的储药柜个数为z5，将上述数学模型结合每种药品的日最大需求量，代入实际的数据，用数学软件计算可以得出最小的储药柜个数z5=4。

模型四又是在前三个模型的基础上，考虑了横纵向隔板间距类型最少、槽宽高总冗余最小、以及药盒在储药槽内推送过程中不会出现并排重叠、侧翻或水平旋转，同时结合每一种药品编号对应的最大日需求量数据，在储药槽的长度为1.5 m，每天仅集中补药一次的情况下，建立了模型四，计算出了每一种药品需要的储药槽个数mi，和最少需要的储药柜个数z5。该模型符合实际，充分利用了数学软件求得了结果，所得的误差较小，结果准确合理。

3 结束语

文中没有考虑隔板的厚度，在以后的改进中希望能考虑到隔板的厚度，这样能设计出更合理的储药柜。通过建立宽度、高度与冗余的数学模型，较好的的设计出符合实际的储药柜。建立的模型原理简单易懂，简化了算法，切实可行，较好的解决了一般的储药柜不考虑药盒实际、横纵向等距的设计，造成药盒与上下横向隔板之间以及左右纵向隔板之间很大的高度和宽度冗余；同时又要使横纵向隔板的间距类型尽可能少以增加储药槽的应用范围，这样的矛盾问题通过建立合适的数学模型得到了解决。

参考文献：

[1] 孙晓娟，刘晓可. 储药柜的设计数学模型的分析与求解[J]. 才智，2015（2）：139.

[2] 韩中庚. 数学建模方法及其应用[M]. 2版.北京：高等教育出版社，2009.

[3] 谢金星，薛毅. 优化建模与LINDO/LINGO软件[M]. 北京：清华大学出版社，2005.

[4] 白其峥. 数学建模案例分析[M]. 北京：海洋出版社，2000.

[5] 刘仁云. 数学建模方法与数学实验[M]. 北京：中国水利水电出版社，2011.

[6] 姜启源，谢金星，叶俊. 数学模型 [M]. 3版. 北京：高等教育出版社，2003.

（责任编辑：徐兴华）