LINGO在运筹学实践教学中的应用

管梅

【摘 要】运筹学是一门研究如何有效地组织和管理人机系统的科学，在许多学科领域及实际问题中均有应用。自从运筹学在20世纪30年代建立以来，其算法的发展一直受到电子计算机的发展的影响。由此可见，在本科运筹学教学中引入适当的实践教学是相当有必要的。本文结合教学实践，介绍了优化建模软件LINGO在运输问题，0-1规划和最短路问题中的应用，有助于提高学生的学习兴趣，感受运筹学课程的实用性。

【关键词】运筹学； LINGO；运输问题；0-1规划；最短路

0 引言

运筹学是20世纪30年代末产生的应用学科，已经在生产管理、工程技术、军事战争、科学实验、经济管理以及社会科学中都得到了极为广泛的应用，与此同时，运筹学的理论应用中得到了长足的发展。20世纪50年代后，计算机的迅猛发展和广泛应用，为运筹学的发展创造了有利的技术条件，使得运筹学的方法论能成功地、及时地解决大量经济管理中的决策问题[1]。计算机的发展推进了运筹学的发展、普及和应用，使得它不仅仅为“运作研究”小组那样的专家所掌握和使用，也成为广大经济管理、系统科学、信息与计算科学等专业的工作者进行最优决策和有效管理的常用工具之一[2]。在运筹学实际教学过程中，很多老师还是重理论轻实践，导致很多学生在学了运筹学之后，只是觉得运筹学理论高深、具体算法难以实现，感觉不到运筹学的实际应用价值。通过优化软件可以使得学生有机会自己动手解决有一定规模的实际问题，缩小学生课堂所学知识与实际运用之间的差距，从而激发其学习兴趣。

LINDO/LINGO 是由美国芝加哥大学的Linus Schrage教授于1980年前后开发出来的一套专门用于求解最优化问题的软件包，经过多年的不断完善和扩充所形成的，并成立LINDO系统公司（LINDO Systems Inc.）进行商业化运作，取得巨大的成功[3]。LINGO 是Linear Interactive and General Optimizer的缩写，即“交互式的线性和通用优化求解器”，可以用于求解非线性规划，也可以用于一些线性和非线性方程组的求解等。其特色在于可以允许决策变量是整数（即整数规划，包括0-1整数规划），方便灵活，而且执行速度非常快。

1 实例应用

一般地，使用LINGO 求解运筹学问题可以分为以下两个步骤来完成：1）根据实际问题，建立数学模型，即使用数学建模的方法建立优化模型；2）根据优化模型，利用LINGO 来求解模型，借助于计算机来求解。

1.1 在运输问题中的应用

在经济建设中，经常碰到大宗物资调运问题。如煤、钢铁、木材、粮食等物资，在全国有若干生产基地，根据已有的交通网，应如何指定调运方案，将这些物资运到各消费地点，而总运费最小，这就是经典的运输问题[4]。

表1 产销量、单位运价表

例1 某煤炭供应商有7个煤矿（产地），开挖的煤炭供应给9个发电站（销地），各煤矿的生产量、各发电站的需求量（假定单位均为t），以及煤炭从各煤矿运到各个发电站的单位运价示于表1中，要求研究煤炭如何调运才能使总运费最小？

解：设xij（i=1，2，…，7；j=1，2，…，9）为从Ai煤矿运到Bj发电站的煤炭的数量，建立该运输问题的数学模型如下：

其中cij为将煤炭从Ai煤矿运到Bj发电站的单位运输费用，ai为煤矿Ai的产煤量，bj为发电站Bj对煤炭的需求量。

应用LINGO来求解该模型，只需要在LINGO窗口中输人以下代码：

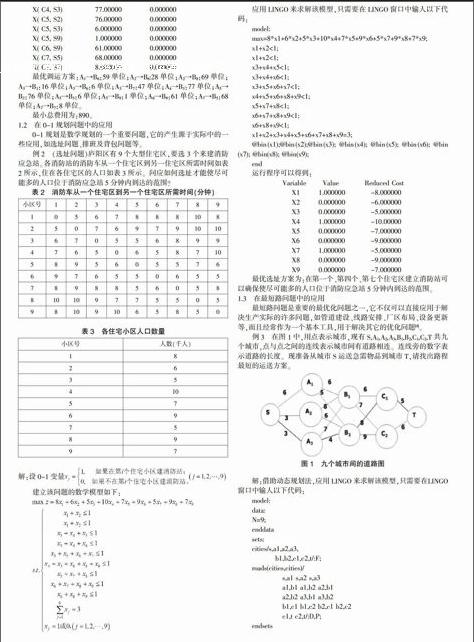
最优调运方案：A1→B6：59单位；A2→B6：28单位；A2→B8：69单位；A3→B1：16单位；A3→B6：6单位；A3→B7：47单位；A4→B3：77单位；A5→B2：76单位；A5→B3：6单位；A5→B9：1单位；A6→B9：61单位；A7→B5：68单位；A7→B7：8单位。

最小总费用为：890。

1.2 在0-1规划问题中的应用

0-1规划是数学规划的一个重要问题，它的产生源于实际中的一些应用，如选址问题、排班及背包问题等。

例2 （选址问题）庐阳区有9个大型住宅区，要选3个来建消防应急站。各消防站的消防车从一个住宅区到另一住宅区所需时间如表2所示，住在各住宅区的人口如表3所示。问应如何选址才能使尽可能多的人口位于消防应急站5分钟内到达的范围？

最优选址方案为：在第一个、第四个、第七个住宅区建立消防站可以确保使尽可能多的人口位于消防应急站5分钟内到达的范围。

1.3 在最短路问题中的应用

最短路问题是重要的最优化问题之一，它不仅可以直接应用于解决生产实际的许多问题，如管道建设、线路安排、厂区布局、设备更新等，而且经常作为一个基本工具，用于解决其它的优化问题[4]。

例3 在图1中，用点表示城市，现有S，A1，A2，A3，B1，B2，C1，C2，T共九个城市，点与点之间的连线表示城市间有道路相连。连线旁的数字表示道路的长度。现准备从城市S运送急需物品到城市T，请找出路程最短的运送方案。

图1 九个城市间的道路图

解：借助动态规划法，应用LINGO来求解该模型，只需要在LINGO窗口中输人以下代码：

2 结语

以上三个实例由于变量个数多，如果是借助算法进行手工计算工作量是非常大的，会让学生感到繁琐不易学会，而借助LINGO作为辅助工具来进行实践教学，不仅使学生从大量的计算中解脱出来，更能激发学生对运筹学课程的学习兴趣，提高实际应用能力，体会到应用数学的实用性。

【参考文献】

[1]胡运权.运筹学教程[M].3版.北京：清华大学出版社，2007：1-10.

[2]韩伯棠.管理运筹学[M].2版.北京：高等教育出版社，2005：1-8.

[3]谢金星.优化建模与LINDO/LING0软件[M].北京：清华大学出版社，2005，7.

[4]《运筹学》教材编写组.运筹学[M].2版.北京：清华大学出版社，2009，1：80-90.

[责任编辑：汤静]