高阶振型阻尼对混凝土框剪结构抗震延性折减系数的影响*

赵卫锋， 李欣俊, 刘正才， 龙志林

(湘潭大学 土木工程与力学学院，湖南 湘潭 411105)

高阶振型阻尼对混凝土框剪结构抗震延性折减系数的影响*

赵卫锋*， 李欣俊, 刘正才， 龙志林

(湘潭大学 土木工程与力学学院，湖南 湘潭 411105)

研究高阶振型阻尼对高层钢筋混凝土框架剪力墙结构抗震延性折减系数的影响.采用5条地震动记录，通过平面结构的地震弹塑性动力时程分析和静力弹塑性分析，以系统位移延性为指标，探讨结构振型阻尼组合数与刚度特征值、竖向不规则对延性折减系数的综合影响.结果表明：振型阻尼组合数对延性折减系数有重要影响，延性折减系数随振型阻尼组合数增加逐渐减小，当振型阻尼组合数较大时，会处于稳定；振型阻尼组合数与刚度特征值对延性折减系数有交互影响，而振型阻尼组合数与竖向不规则对延性折减系数的交互影响不显著.

框剪结构；高阶振型阻尼；延性折减系数；刚度特征值；竖向不规则；抗震

结构抗震强度折减系数既是基于承载力(强度)抗震设计中确定设计地震作用的关键因素，又是基于性态抗震设计理论中确定非弹性反应谱的主要依据.强度折减系数定义为结构保持完全弹性所需要的最低承载力与结构保持给定延性水准所需要的最低承载力之比.关于结构抗震强度折减系数在国际抗震设计规范中的应用情况以及国内外的研究现状，翟长海[1,2]归纳介绍了详细发展动态.我国抗震设计规范没有直接体现抗震强度系数，而是采用小震设计的概念，其本质是相似的，即由结构影响系数C(强度折减系数的倒数,约0.35)考虑结构延性耗能的影响折减基本设防烈度弹性地震强度到小震水平[3].

结构抗震强度折减系数可以分解为基于延性耗能的延性折减系数、基于阻尼耗能的阻尼折减系数和基于系统超强能力的超强折减系数，如式(1)所示：

R=RμRxRs,

(1)

式中，R为强度折减系数；Rμ为延性折减系数；Rx为阻尼折减系数；Rs为体系超强折减系数.

国内外现有强度折减系数研究中的不足是研究对象主要针对剪切变形为主的框架结构或多自由度楼层模型[4,5]，以弯剪变形为主的框剪结构体系为对象的研究文献较少.多自由度体系延性折减系数研究方法中，一般仅指定结构前2～3阶振型阻尼比[5]，而忽略高阶振型阻尼的影响，阻尼相关的影响只聚焦于阻尼折减系数研究之中[6].事实上，延性折减系数与阻尼折减系数有很显著的关联，因为动力时程分析结果与初始指定的阻尼比大小、振型阻尼组合数、高阶振型阻尼与前几阶振型阻尼的比例关系等均有关系[7].已有研究表明不同结构体系对高模态(高阶振型)的敏感程度不相同，忽略高模态效应计算的等效地震作用可能导致不合理的抗震设计[7～10].高阶振型阻尼对延性折减系数(或强度折减系数)的影响是否显著，国内外的研究很少.高层混凝土框剪结构一般楼层高、高阶振型复杂、结构刚度特征值影响结构侧移模式和楼层剪力分配.此外，结构竖向刚度和承载力不连续也影响结构的高阶振型模式.为此，本文通过高层钢筋混凝土平面框剪结构的地震弹塑性动力时程分析和静力弹塑性分析，以结构系统位移延性需求为评价指标，探讨振型阻尼组合数与刚度特征值、楼层屈服承载力变化和刚度变化对延性折减系数的影响，为等效静力抗震设计方法提供参考.

1 输入地震动、框剪数值结构及分析方法

1.1 输入地震动

不同的震源机制对于结构地震响应的影响较大，为了避免震源机制的干扰和影响，选择1999年台湾集集地震水平向记录5条(表1)，以加速度峰值(PGA)作为地震强度表征数.记录来源于美国太平洋地震工程研究中心(PEER)强震数据库[11].为消除不同记录场地差异的影响，采用软件SeisMomatch[12]将原始记录匹配为坚硬土场地特性(800 cm/s≥Vs>500 cm/s)的记录.匹配加速度反应谱与设计反应谱(第2组)的比较如图1所示.

表1 分析采用的地震动记录

Tab.1 Ground motions records used in analysis

记录站台PGA/gPGV/(cm·s-1)CHY065⁃W0．11815．8ILA007⁃N0．08910．6ILA⁃012⁃W0．08816．1ILA013⁃N0．14921．6ILA016⁃W0．08215．1

1.2 框剪数值结构

15层和30层钢筋混凝土平面框剪结构的立面示意如图2所示，结构的跨度分别为4.5 m和7.0 m，底层层高4.0 m，其他各层为3.0 m.地震弹塑性动力时程分析和静力弹塑性分析采用专业结构分析软件CANNY2012.根据梁柱构件的截面尺寸、混凝土强度等级以及配筋信息等计算出梁柱单元的刚度和承载力，采用三线性滞回规则定义梁柱单元弯矩-曲率关系和框架柱轴向拉压-变形关系，不考虑单元剪切变形.梁、柱、剪力墙的参数值如表2～4所示.采用此类数值结构的优势：在任意峰值加速度的地震作用下，结构的弹塑性动力时程分析均可以得到全时程的收敛结果；修改结构竖向刚度和承载力分布模式较方便.与纤维模拟单元比较，指定弯矩-曲率关系单元的不利因素是不能考虑梁柱承载力的压-弯交互作用，但在地震位移反应分析结果方面差异较小.

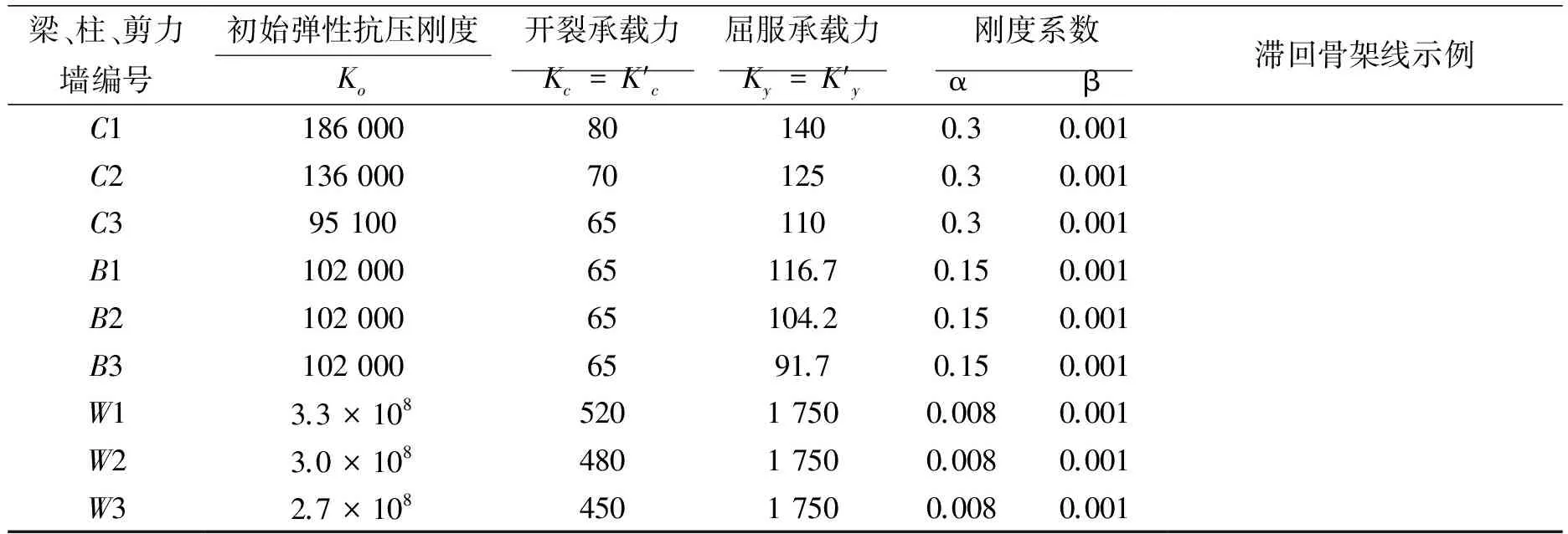
表2 15层结构梁、柱、剪力墙的抗弯参数

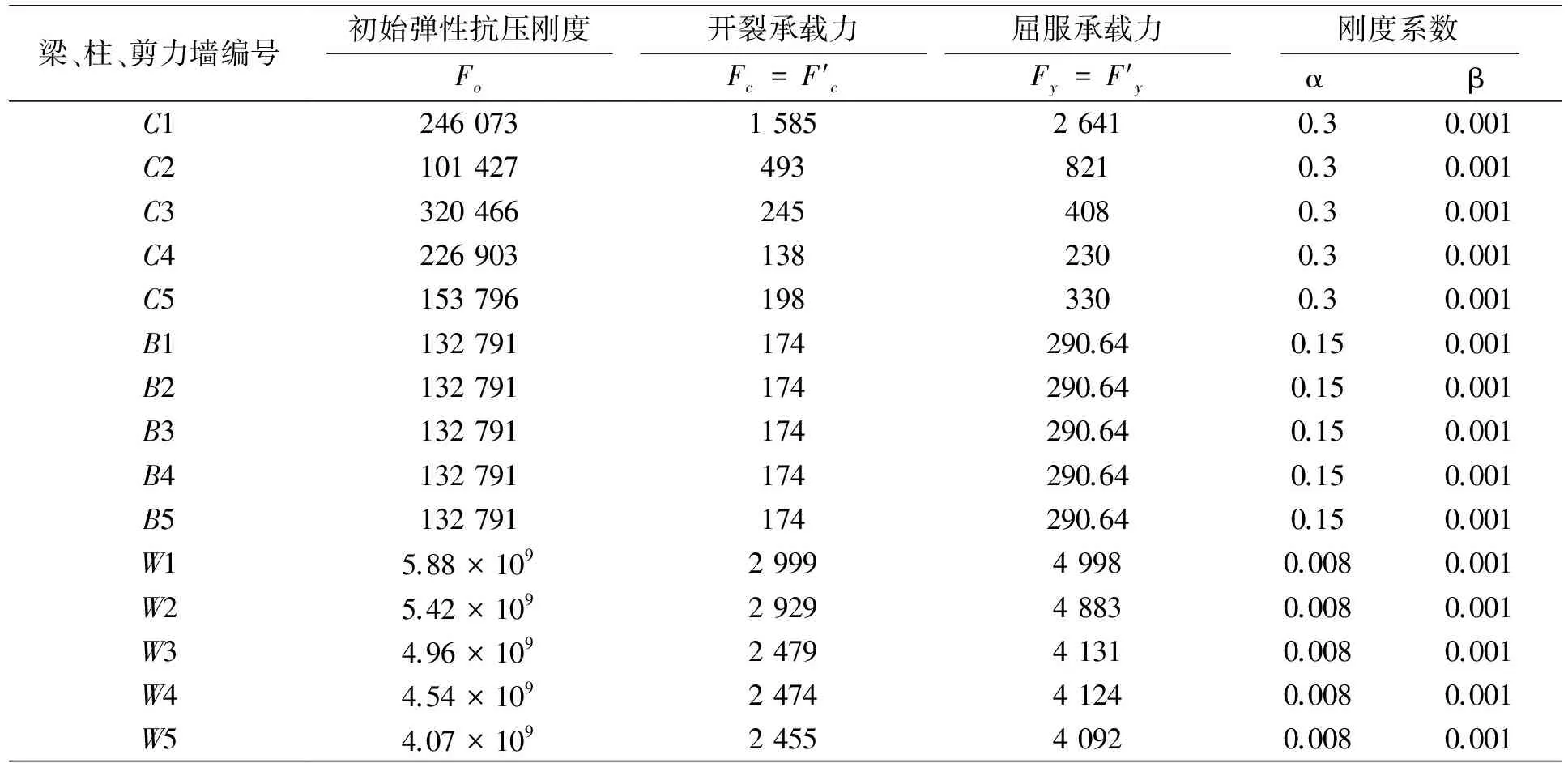
表3 30层规则结构梁、柱、剪力墙单元的抗弯参数

表4 柱单元的抗拉压参数

1.3 分析方法

首先通过弹塑性动力时程分析计算结构最大层间位移dm，通过弹塑性静力分析确定结构层间屈服位移dy，然后按式(2)计算位移延性系数

μ=dm/dy，

(2)

定义考虑高阶振型阻尼影响的延性折减系数的修正系数为Rx：

(3)

把Nassar[13]研究的位移延性与延性折减系数关系式(4)以及式(2)代入式(3)，只需计算最大位移延性就可以求出修正系数Rx.

(4)

式中，Rμ表示延性折减系数；μ表示延性系数；T表示结构第一自振周期；a，b表示与结构系统相关的参数，在本文中取a=1.01，b=0.37.

此外，指定所有考虑的振型阻尼比均为0.05.依据以下条件共进行2 080次动力时程分析：5条地震动加速度记录，2种楼层结构(15和30层)，中间层4种层承载力不规则变化率(0.7、0.8、0.9和1.0)，中间层4种层刚度不规则变化率(0.8、0.85、0.9和1.0)，4种刚度特征值(1.5、3.0、4.5和6.0)，15层结构5种高模态组合数(1，3，7，11，14)，30层结构8种高模态组合数(1，3，7，11，14，20，26，30).

2 数值分析结果与讨论

2.1 振型阻尼组合数对结构地震反应分布模式的影响

以30层结构为例，地震作用下结构进入弹塑性阶段后，振型阻尼组合数对结构地震反应分布模式的影响如图3所示.考虑4种振型阻尼组合数对楼层剪力和结构侧移的影响，随着阻尼组合数的增大，楼层剪力和结构侧移逐渐减小，但位移的相对变化明显比楼层剪力大(数量级不同)，因此采用位移延性系数研究此问题更合适；振型阻尼组合数较大时，楼层剪力和层位移变化甚微；高阶振型阻尼对楼层剪力和侧移地震反应分布模式影响不大.

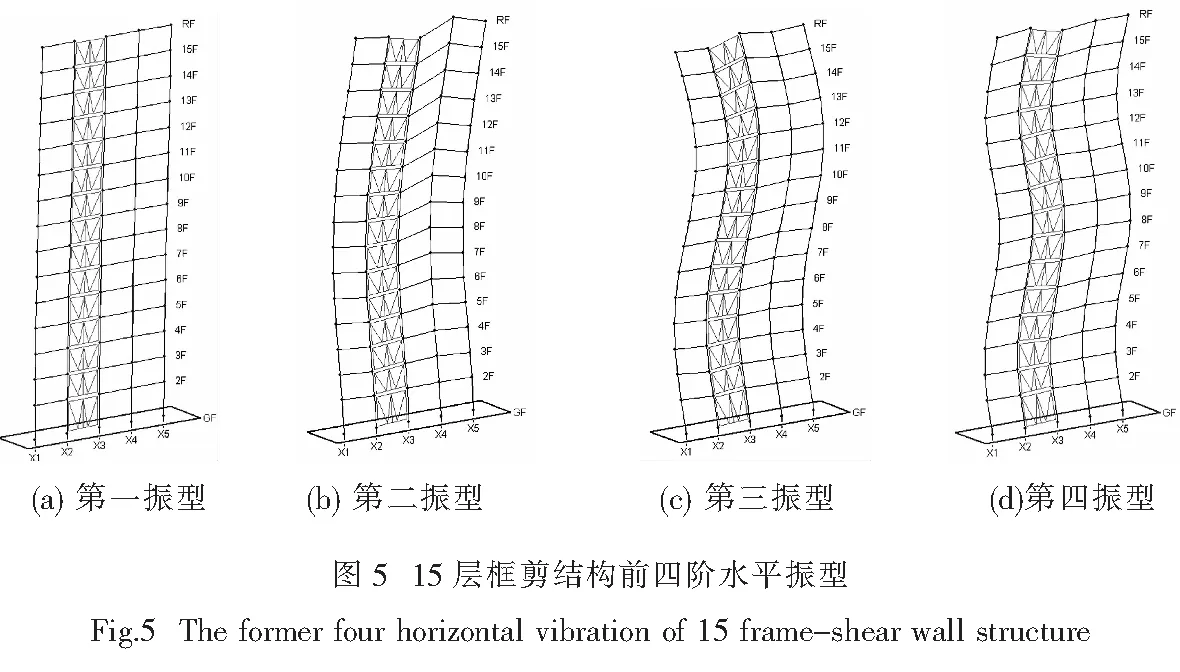
2.2 振型组合数的影响

2.3 刚度特征值影响

框剪结构刚度特征值是体现总框架抗侧移刚度和总剪力墙抗弯刚度之比的一个参数，对框架剪力墙结构的受力状态和变形及外力的分配都有很大的影响.从图7可知，刚度特征值对修正系数有影响，15层结构随刚度特征值增大先增大后减小，之后基本稳定；30层结构随增大而增大，之后处于稳定.总体上是增大的，表明以弯曲变形为主的剪力墙结构的修正系数向以剪切变形为主的框架结构的修正系数过渡.

2.4 竖向不规则的影响

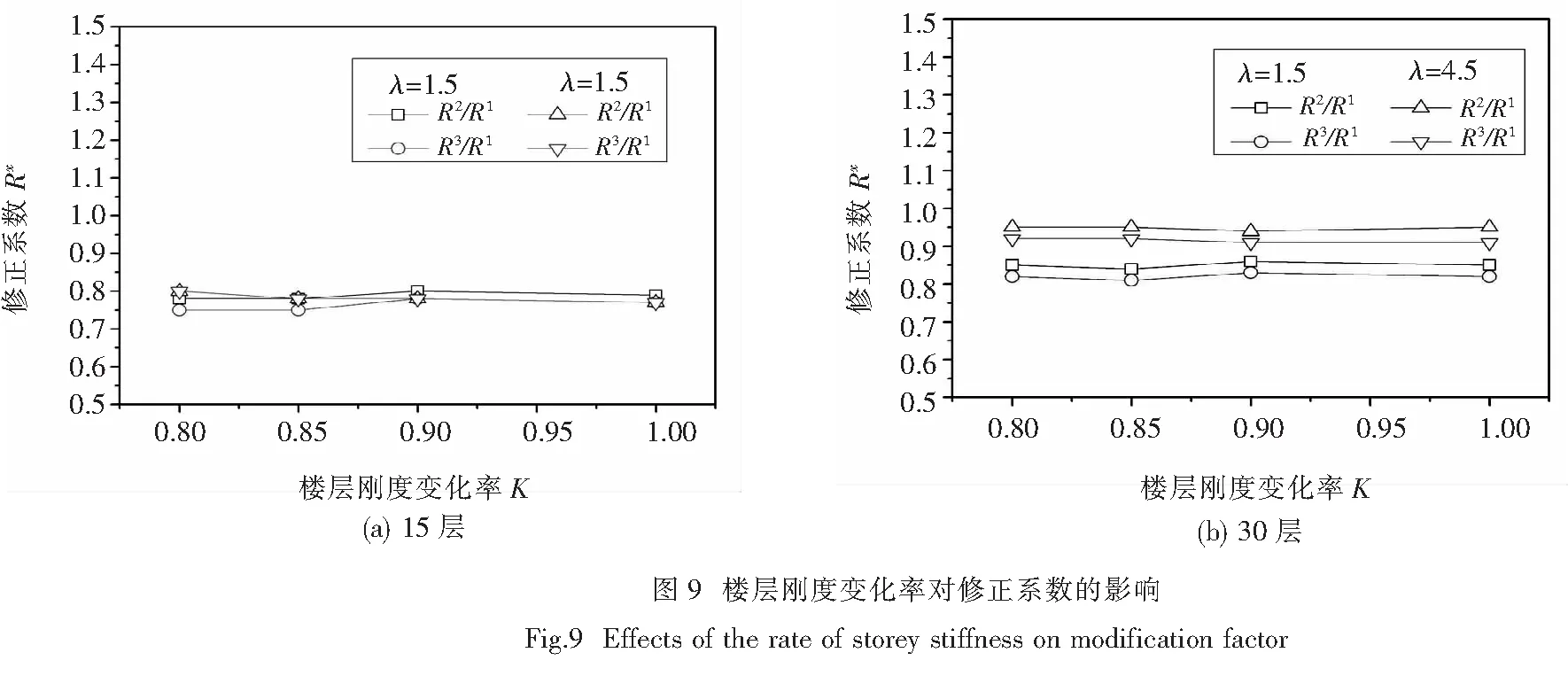
结构竖向楼层刚度和承载力不连续对结构的高阶振型和地震位移反应模式等的影响很大，是结构设计中应尽量回避或重点考察的内容.但考虑竖向不规则和振型组合数对延性折减系数的耦合影响，在本文的研究中并不显著.如图8和图9所示，改变中间楼层(15层的第8层，30层的第15层)的刚度和屈服承载力，虽然修正系数有些变化，但整体变化幅度不大.因此，可不考虑竖向不规则对修正系数的影响.

3 结 论

研究了高振型阻尼对框剪结构的延性折减系数的影响，得到如下结论：

(1) 高振型阻尼对延性折减系数有影响，考虑高阶振型阻尼影响的延性折减系数的修正系数随着振型组合数的增加而减小，减小到一定程度会保持稳定.

(2) 结构刚度特征值和振型数组合数对延性折减系数有交互影响，延性折减系数随刚度特征值先增大再减小，而后趋于稳定.

(3) 结构竖向不规则和振型数组合数对延性折减系数有些交互影响，但影响幅度很小.

[1] 翟长海, 谢礼立. 抗震规范应用强度折减系数的现状及分析[J]. 地震工程与工程振动, 2006, 26(2):1-7.

[2] 翟长海, 谢礼立. 结构抗震设计中的强度折减系数研究进展[J]. 哈尔滨工业大学学报, 2007, 39(8):1 177-1 184.

[3] 陈国兴. 中国建筑抗震设计规范的演变与发展[J]. 防灾减灾工程学报, 2003, 23(1):102-113.

[4] 翟长海, 谢礼立. 多自由度体系效应对强度折减系数的影响[J]. 工程力学, 2006, 23(11):33-37, 69.

[5] MOGHADDAM H, MOHAMMADI R K. Ductility reduction factor of MDOF shear-building structures [J]. Journal of Earthquake Engineering, 2001, 5(3): 425-440.

[6] 周靖，周飞. 地震动持时效应对阻尼折减系数的影响 [J]. 工程力学，2009,26(2):78-84.

[7] 唐谢兴，张友亮. 结构动力时程分析中的阻尼问题研究 [J]. 建筑结构，2006, 36(S):57-64.

[8] DANESHJOO F, GERAMI M. Higher mode effects on seismic behavior of MDOF steel moment resisting frames [J].Journal of Sustainable Energy and Environment，2003, 5(3): 41-54.

[9] 祝文畏，杨学林，岳燕玲.竖向质量分布对框架结构动力特性影响的研究[J]. 地震工程与工程振动, 2011,31(5): 97-103.

[10] 辛力，梁兴文，曾凡生，等. 混凝土剪力墙结构考虑高振型影响的基于位移的抗震设计[J]. 建筑结构学报，2010, 31(9):27-34.

[11] Pacific earthquake engineering research center, strong motion database [EB/OL].http://peer.berkeley.edu.2012-10-25.

[12] Seismomatch, software for adjusting earthquake accelerograms to match a specific target response spectrum [CP].

[13] NASSAR A, KRAWINKLE H. Seismic demands for SDOF and MODF systems [D].USA:Stanford University,1997.

责任编辑：罗 联

Effects of Higher Modal Damping on Seismic Ductility Reduction Factors for Concrete Frame-Shear Wall Structures

ZHAOWei-feng*,LIXin-jun,LIUZheng-cai，LONGZhi-lin

(College of Civil Engineering and Mechanics, Xiangtan University, Xiangtan 411105 China)

The effects of higher modal damping on seismic ductility reduction factor for the concrete frame-shear wall buildings are studied. Based on the planar structure and using 5 ground motions, the elastoplastic dynamic history analysis and static elastoplastic pushover are performed to investigate the coupling effects of the modal damping number and the stiffness characteristic value, the vertical irregularity of structure on seismic ductility reduction factor on the basis of the global displacement ductility. The results demonstrate that the modal damping number has important effects on seismic ductility reduction factor. Ductility reduction factor decreases with the increasing of the modal damping number, and it is almost invariant as to consider more modal damping number. Modal damping number and stiffness characteristic value have important interaction effects on ductility reduction factor, while modal damping number and vertical irregularity have indistinctive interaction effects.

frame-shear wall structure; higher modal damping; ductility reduction factor; stiffness characteristic value; vertical irregularity; seismic

2014-04-02

湖南省自然科学基金项目(12JJ2024)；国家自然科学基金项目(51471139，51071134)；湖南省科技计划项目 (2014SK4062)；湘潭市科技计划项目(S2013N0013)

赵卫锋(1978— ),女，湖南 益阳人，博士生.E-mail:weifengzhjing@163.com

TU318+.1

A

1000-5900(2015)01-0024-07