均布荷载作用下四边简支单向筒芯空心楼盖弹性分析*
2015-04-28肖静宇
刘 忠, 肖静宇
(湘潭大学 土木工程与力学学院,湖南 湘潭 411105)
均布荷载作用下四边简支单向筒芯空心楼盖弹性分析*
刘 忠*, 肖静宇
(湘潭大学 土木工程与力学学院,湖南 湘潭 411105)
针对单向筒芯空心楼盖两个方向变截面刚度的问题,采用刚度均匀化的方法将空心薄板比拟成正交异性板.计算四边简支条件下,正交异性矩形薄板在竖向均布荷载作用下的挠度值,并分析在不同参数情况下板的挠度变化.可以得出:在一定范围内,板中心点处的挠度值随着顺筒方向筒间距的增加以近似线性的趋势减小;挠度值随着筒直径的增大而逐渐增加,且增速由慢到快;随着板厚的增加,挠度值减小速度由快到慢.
空心楼盖;平均刚度;正交异性板;四边简支;挠度
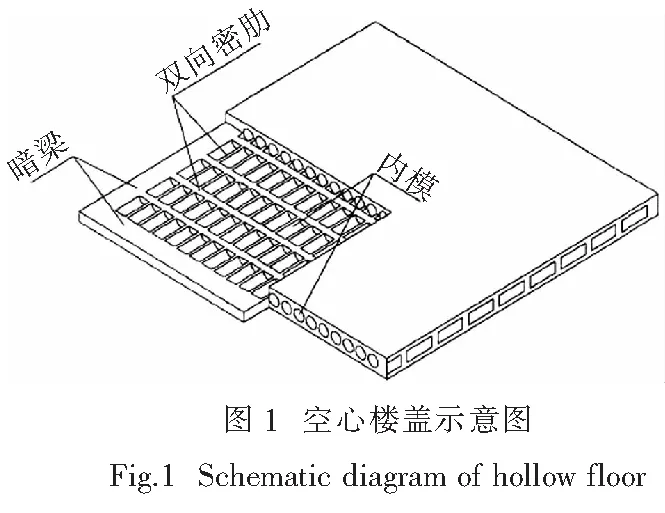
楼盖体系是建筑结构的重要组成部分,为了更好地满足建筑中高楼层、大跨度、多隔墙等特点,最大限度自由地进行空间布置,就需要更经济合理的楼盖形式出现在建筑中.单向筒芯内模空心楼盖是现浇空心楼盖中的一种,即在现浇钢筋混凝土楼盖中采用埋芯成孔工艺,在楼盖内每隔一定距离放置圆形高强薄壁复合管,孔道是单向的,然后浇筑混凝土而成.其质量轻、高度小、整体性好等性能可以更好地满足当代建筑要求.
一直以来学者们对空心楼盖的理论分析开展了大量研究工作.1994年,青岛建筑工程学院曲庆璋等通过经典弹性理论求解出正交各向异性矩形薄板线弹性弯曲的一般解析解[1];2001年,东南大学吕志涛院士、张继文教授提出了变刚度双向板内力的能量法计算[2];2003年,王茂、杨建军提出了用虚拟交叉梁分析法分析现浇钢筋混凝土空心无梁楼盖[3];2004年,张华刚、马克俭等提出了空心板楼盖的连续化分析方法[4];2008年,管品武、唐国斌通过构造比拟正交异性板法来计算空心楼盖变形和内力[5].
针对单向筒芯空心楼盖两个方向变截面刚度的问题,本文通过刚度均匀化的方法将空心薄板比拟成正交异性板.计算四边简支条件下,正交异性矩形薄板在竖向均布荷载作用下的挠度值,并分析在不同的参数(板厚,管端间距,筒直径)情况下板中心点处的挠度变化.
1 基本假定、基本方程及求解
1.1 基本假定
单向筒芯内模空心楼盖[6]由于其筒芯及间肋的存在,导致两个方向的刚度是变化的.这种结构均匀化处理后的刚度在相互垂直的两个方向上有所不同,造成构造上的各向异性,实质上是一种正交各向异性的矩形薄板.本文以不考虑剪切变形影响的经典薄板理论[9]为基础进行讨论,其基本假设如下:
(1) 位移变形是微小的,板的中平面不发生变形,即忽略板内的薄膜力(板平面内的轴力),只考虑板受弯.
(2) 板变形后,法线仍为垂直于板中面的直线,即忽略板内垂直于板平面方向的剪切应力.
(3) 板中各个平行层间不挤压,即忽略板内垂直于板平面方向的正应力.
(4) 在一般情况下,与结构尺寸相比,距离微小的构件所组成的结构,其相邻构件间应力、变形差异很小,可以作连续化处理.
(5) 板内筒芯存在区域,截面的变化近似按线性处理.

1.2 基本方程与边界条件
根据参考文献[10]可知,正交异性板的挠曲微分方程为:
(1)
式中,H=D1+2Dk,为正交异性板折算刚度;Dx,Dy为薄板在弹性主方向的抗弯刚度;Dk为薄板在弹性主方向的抗扭刚度.
对于四边简支的矩形薄板,其中长为L,宽为B,当薄板的弹性主向与边界平行,坐标轴如图3所示.

(2)
当空心楼盖为四边简支时,利用纳维法求解方法,求得方程(1)的解为:
(3)
可以满足上述关于挠度和弯矩的边界条件.
当薄板受均布荷载时,q成为常量q0,可导出
(4)
1.3 刚度的均匀化
单向筒芯内模空心楼盖中圆形空心管在平面上的单向排列,使得板在纵、横两个方向上的截面是变化的,但由于这种变化是有规律的重复,可以用平均刚度来反映这种变截面的刚度[13].
一般所指的正交异性板,其特点是结构材料在X和Y两个方向的弹性性质不同,如以弹性性质的对称面作为坐标面,其应力与应变关系[12]为:
(5)
根据经典弹性薄板理论,截面的应变和挠度关系为:
(6)
根据式(5),(6)积分可得空心楼盖横筒和顺筒方面单元段的内力:
(7)

(8)

肋梁的扭转变形与内力关系为:
(9)
式中Jbw和Jbf分别为横筒、顺筒方向肋梁抗扭惯性矩.同理,对公式(9)进行积分可得:

(10)
在公式H=D1+2Dk中:D1=(Dx1+Dx2)/2,2Dk=(Dkx+Dky)/2.
在空心板的横肋与纵肋的截面处,其截面特征同实心板的截面相同,所以对一单元段截面:
(11)
由上可导出截面平均刚度:
(12)
式中:ν为泊松比;E为混凝土的弹性模量;G为混凝土的简变模量.
对于简支薄板来说,最大挠度发生在板的中心,即x=L/2,y=B/2,代入(4)可得:
(13)
由于上述级数收敛较快,可取其前四项进行计算:m=1,n=1,3;m=3,n=1,3.
(14)
将式(12)代入式(14)中进行相关挠度的计算.
2 结果分析
结合式(4)和式(12)可知:当板的尺寸为B=4 m,L=5 m时,取x=2.5 m,顺筒方向板中线处随坐标值Y变化的挠度值如图4所示;取y=2.5 m,横筒方向板中线处随坐标值X变化的挠度值如图5所示.可知,在弹性阶段顺筒方向挠度值变化的趋势较横筒方向较快.

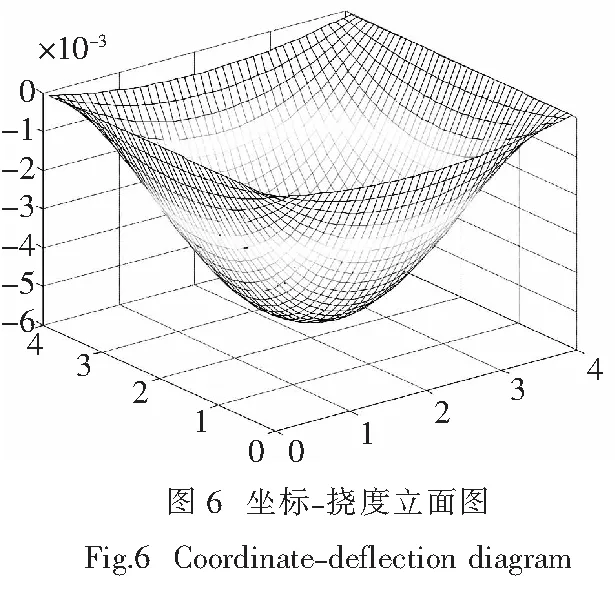
当板的尺寸为B=4m,L=4m时,根据式(4)可得板的坐标-挠度立面图[8].可知:在均布荷载q=4.4 kN/m作用下四边简支正交异性板的变形图近似漏斗状,四边挠度值为零,距离中心点越近,挠度值越大,并且在中心点处取得最大值wmax=0.545 69 mm.
从图6可看出板中心点处的(即x=2 m,y=2 m)挠度值最大,本文取板的中心点进行分析.利用上述公式计算在不同荷载作用下板中心点的挠度值,与试验值[7]对比,验证本文用正交异性板法对单向筒芯空心楼盖进行力学分析的可靠性.其中当荷载为q=4.4 kN/m时,计算得到挠度值w=0.542 mm.

从图7可以看出:在弹性阶段不同荷载作用下的四边简支正交异性板的挠度曲线与实验值有一定的吻合,说明用正交异形板法进行单向筒芯空心楼盖的力学分析有一定的可靠性.
从图8~10中可以观察到:在弹性阶段,随着筒端间距、筒直径及板厚的增大,板中心点处挠度值依次随之减小、增大、减小.从图8中可以观察到:当管端间距控制在50~400mm范围时,随着筒端间距的增加,空心板中心点的挠度值以近似线性的趋势减小,故随管端间距增加,在一定程度上减少了板挠度值.从图9可以看出,当增大筒直径时,空心板中心点处的挠度值以近似二次曲线的趋势增加,增长速度越来越快,当筒直径超过80mm时,挠度值增速明显加快.因此,单向筒芯空心楼盖随着筒直径的增加,空心板中心点处挠度值增速由慢到快.由图10可知,当板厚在80~180mm范围内,随板厚的增加,空心板中心点处挠度值减小速度由快到慢;当空心板厚超过160mm时(接近筒直径的两倍),挠度值变化较慢.因此,当单向筒芯空心楼盖筒芯直径接近板厚的一半时达到最优值.

3 小 结
以经典薄板理论为基础,采用刚度均匀化的方法将空心薄板比拟成正交异性板,进行均布荷载作用下四边简支单向筒芯空心楼盖的弹性分析,得到如下结论:
(1) 在弹性阶段,单向筒芯空心楼板顺筒方向挠度值变化的趋势较横筒方向较快.板中心点处的挠度值与所受竖向均布荷载呈线性关系.
(2) 随着管端间距、筒直径及板厚的增大,板中心点处挠度值也依次随之减小、增大、减小.
(3) 当管端间距控制在一定范围内时,板中心点处的挠度值以近似线性的趋势减小,在一定范围内增加管端间距对减小板的挠度值有较好的效果.
(4) 单向筒芯空心楼盖随着筒直径的增加,板中心点处的挠度值以近似二次曲线的趋势增加,挠度值增速由慢到快.
(5) 随板厚的增加,空心板中心点处挠度值减小速度由快到慢;当空心板厚接近筒直径的两倍时,挠度值变化较慢.因此,当单向筒芯空心楼盖直径接近板厚的一半时达到最优值.
[1] 曲庆璋,梁兴复,章权.正交各向异性矩形板弯曲问题的一般精确解[J].青岛建筑工程学院学报,1994,15(2):53-59.
[2] 张继文,吕志涛.变刚度双向板内力的能量法计算[J].工业建筑,2001,31(12):73-75.
[3] 王茂,杨建军.现浇钢筋混凝土空心无梁楼盖的虚拟交叉梁分析法[J].长沙铁道学院学报,2003,21(2):40-45.
[4] 张华刚,马克俭.现浇钢筋混凝土空心板楼盖的连续化分析[J].空间结构,2004,10(4):12-15.
[5] 管品武,唐国斌.正交异性板法分析现浇混凝土空心楼盖[J].四川建筑科学研究,2008,34(6):58-60.
[6] 邱则有.现浇混凝土空心楼盖[M].中国建筑工业出版社,2007:103-133.
[7] 程文瀼,江韩.圆管式无柱帽空心无梁楼盖的试验研究[J].建筑结构学报,2004,25(5):78-84.
[8] 张洪学,张云龙,白成祥.边支承现浇空心板设计计算与软件实现[J].建筑结构,2006,36(3):91-94.
[9] 沈蒲生.楼盖结构设计原理[M].北京:科学出版社,2003.
[10] 吴家龙.弹性力学[M].北京.高等教育出版社,2003.
[11] 刘昭清.双向筒芯现浇预应力混凝土双向空心楼板的受力性能研究研究[D].成都:西南交通大学,2010.
[12] TAKABATAKE,YANAGISAWA N. A simplified analysis of rectangular cellular plates[J].Int J Solids Structrures,1999,33(14):789-804.
[13] Gee-Cheol, Joo-Won Kang.Calculation of voided slabs rigidities[J].World Academy of Science,Engineering and Technology,2012,6:664-667.
责任编辑:罗 联
The Elastic Analysis of Four-Edge Simple Supported One-Way Cylinder Hollow Floor under Uniformly Distributed Load
LIUZhong*,XIAOJing-yu
(College of Civil Engineering and Mechanics, Xiangtan University, Xiangtan 411105 China)
For an one-way cylinder core hollow floor had different rigidities in two orthogonal directions, this paper converted a circular voided slabs into an equivalent orthotropic by the method of rigidity homogenization. The deflection of the orthotropic rectangular thin plate under uniformly distributed load,with simply supported on four sides was calculated ,and considering different parameters,we can draw a conclusion: in a certain range, the deflection of the plate of the midpoint decreased with increasing cylinder spacing along the tube direction to approximate linear trend; with the increase of tube diameter,the deflection gradually increased,and the increase speed is from slow to fast; with the increase of the thickness,the deflection decreases,and the decrease speed is from fast to slow.
hollow floor;the average stiffness;orthotropic plate;simply supported on four sides;deflection
2015-01-06
刘忠(1961— ),男,湖南 长沙人,博士,教授.E-mail:359328094@qq.com
TU311.1
A
1000-5900(2015)01-0009-05