基于遗传算法优化BP神经网络的地层破裂压力预测方法

李昌盛，宋 海，肖 莉，杨传书，徐术国

(1.中国石化 石油工程技术研究院，北京 100101； 2.中国石化西北油田分公司 石油工程技术研究院，新疆 乌鲁木齐 830011)

基于遗传算法优化BP神经网络的地层破裂压力预测方法

李昌盛1，宋 海2，肖 莉1，杨传书1，徐术国1

(1.中国石化 石油工程技术研究院，北京 100101； 2.中国石化西北油田分公司 石油工程技术研究院，新疆 乌鲁木齐 830011)

针对地层破裂压力现有预测方法适用性差、误差较大等问题，提出了遗传算法优化BP神经网络(GABP)预测地层破裂压力的方法。分析了地层破裂压力的影响因素；以地层深度、地层孔隙压力当量密度和岩石密度为输入变量，以地层破裂压力当量密度为输出变量，建立了GABP预测地层破裂压力模型，并利用塔里木盆地YB1井的数据进行神经网络学习和结果验证。GABP模型的预测结果误差约3.5%，精度远高于Eaton法。该方法不受地质构造条件影响，且具有精度高、计算速度快等特点。

地层破裂压力；预测模型；BP神经网络；遗传算法

地层破裂压力的预测对钻井中套管柱设计、钻井液、井下测试、固井、压裂方案制定和井下故障控制等方面都具有重要的意义，预测上的误差将可能导致地层被压裂、钻井液漏失，进而造成成本浪费，甚至发生井涌、井喷等钻井事故。目前，地层破裂压力的预测方法很多，主要分为2种：一是地层压裂试验，但是该方法一般只是测定套管鞋处的地层破裂压力，仅限于某些特定深度，难以获取连续地层破裂压力梯度剖面[1]；二是利用测井数据获取连续的岩石力学参数剖面求得地层破裂压力[2]，目前比较常用的模型有Eaton法和黄荣樽法，但是Eaton法考虑参数较少，适用于构造运动较少的连续沉积盆地，而黄荣樽法则需要岩石三轴应力实验和现场地层破裂压力实验数据为支撑才能达到理想效果。另外，这2种方法都是建立在某些特定的假设条件下，如忽视了岩石抗张强度对破裂压力的影响[3]。本文利用BP神经网络建立地层破裂压力预测模型，并引入遗传算法优化网络节点的权值和阈值，提高预测精度和学习效率，通过实例应用证明了该方法的准确性和可靠性。

1 遗传算法优化BP神经网络原理

BP神经网络是一种多层前馈神经网络，该神经网络的主要特点是信号前向传递，误差反向传播。在前向传递过程中，输入信号从输入层经隐含层逐层处理，每一层的神经元状态只影响下一层的神经元状态。如果输出层得不到期望输出，则转入反向传播，根据预测误差来反复调整网络权值和阈值，从而使BP神经网络的预测输入不断逼近期望输出[4]。BP神经网络的非线性映射能力、泛化能力和容错能力使其计算能力远超于常规回归算法，但是它也存在着一些缺陷，比如：网络结构不易确定；传统的梯度下降法经常收敛于局部最优解而不是全局最优解；初始连接权值和阈值的设置难以保证最优等。然而，网络结构、初始连接权值和阈值的选择对网络训练结果的影响很大，这大大限制了BP神经网络的应用范围，降低了应用效果。

为了弥补这一不足，选用遗传算法进行BP神经网络初始权值和阈值的选择。由于遗传算法的优点在于只使用适应度函数，而不采用梯度或其他辅助信息，即使对多态的和非连续的函数关系，依然能够获得全局最优解。它不受函数可微或连续等限制的特点使得遗传算法能够精确计算BP神经网络的节点权值和阈值，且提高了神经网络的学习能力和收敛速度，克服了其弊端。

遗传算法优化BP神经网络(GABP)主要包括3个步骤：BP神经网络的结构确定、利用遗传算法优化权值和阈值以及模型预测。首先，根据所研究变量的输入输出参数个数确定BP神经网络结构，进而确定遗传算法个体的长度。然后，利用遗传算法优化神经网络的权值和阈值。种群中的每个个体都包含了一个网络所有权值和阈值，个体通过适应度函数计算个体适应度值，遗传算法通过选择、交叉和变异操作找到最优适应度值的对应个体[4-6]。适应度函数

(1)

式中：n为网络输出节点数；yi为神经网络第i个结点的期望输出；oi为第i个节点的预测输出；k为系数。

最后，得到最优个体，对网络初始权值和阈值赋值，网络经训练后输出预测函数。

2 地层破裂压力预测GABP模型

2.1 输入输出变量的确定

根据前人的研究成果和现场试验情况，地层破裂压力的影响因素主要包括上覆岩层压力、地层孔隙压力、岩石抗拉强度、泊松比和构造应力等，其中上覆岩层压力主要受岩石密度和地层深度的影响，泊松比代表了地下岩体的固有弹性，是地层岩石塑性的主要指标，一般情况下地层破裂压力随着泊松比的增大而增大[7]，而岩石泊松比很大程度上也由岩石密度决定；岩石抗拉强度和构造应力对地层破裂压力的影响相比其他的因素更小，而且这2个参数实际上都很难获得[8]。因此，综合考虑以上条件，选择深度、地层孔隙压力梯度和岩石密度作为地层破裂压力网络模型的输入变量，输出变量为地层破裂压力梯度。

2.2 学习样本的选择

本文的学习样本来自中石化西北塔里木盆地YB1井的数据，研究井段为750～3 600 m，其中地层包括阿图什组、帕卡布拉克组、安居安组和克孜洛依组等4个层位，岩性组成主要包括砂岩、泥岩和白云岩等。该区属于玛南构造带玛南Ⅵ号构造高部位，压力系统复杂，多处层位易漏，复杂情况多[9]。学习样本中的岩石密度由密度测井所得，地层孔隙压力当量密度是利用测井数据根据等效深度法和有效应力法计算所得。模型训练所用数据经过了多次现场验证和邻井数据的比对，具有较高的准确性。本文模型采用井段较长的阿图什组数据(图1)进行训练，其中整组数据的90%用于神经网络的训练，剩余的10%用于预测模型的验证。

图1 模型学习采用的阿图什组数据

2.3 预测模型建立

根据输入变量数目及模型要求，建立输入节点为3、隐含层节点为7、输出层节点为1的神经网络模型，该网络具有21个权值和8个阈值，遗传算法的个体编码长度为29。模型如图2所示。

图2 BP神经网络拓扑结构

2.4 计算流程

地层破裂压力GABP预测模型的计算流程如图3所示。

2.5 模型评价

经过反复训练，地层破裂压力预测模型的平均适应度曲线经过进化100次后，显示出了很好的收敛性。由图4和图5可以看出最小均方误差值为6.464 4×10-6，达到了最优水平，说明该模型具有很高的精确度。

为了验证模型预测的准确程度，选取YB1井的帕卡布拉克组、安居安组和克孜洛依组井段数据用于模型验证，准备数据如图6和如图7所示。

3 实例验证

为了更好地说明预测结果的准确性，将Eaton法的计算结果与GABP模型预测结果进行对比，如图8、图9和图10所示。结果显示：GABP模型预测结果与实际地层破裂压力梯度的符合性很高，而Eaton法的预测结果则相对偏高。 统计得出， GABP

图3 地层破裂压力GABP预测模型计算流程

图4 适应度变化曲线

图5 均方误差变化曲线

图6 YB1井预测井段要求的地层孔隙压力数据

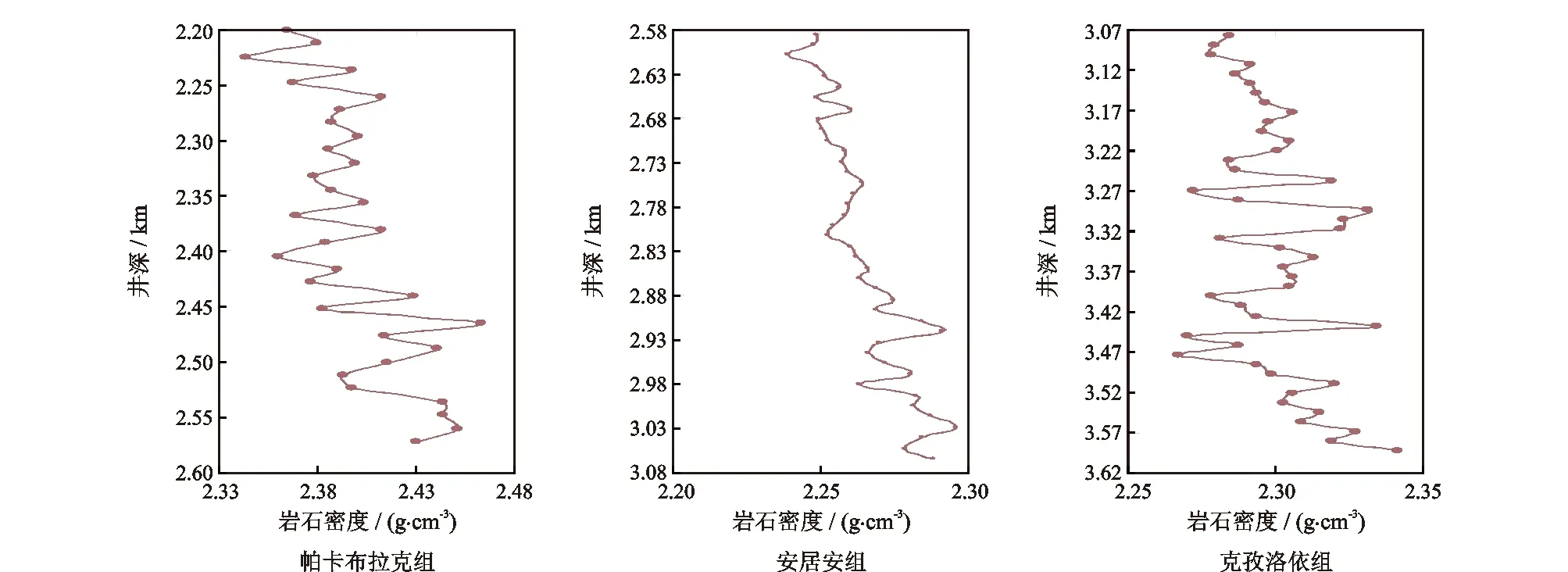
图7 YB1井预测井段的地层岩石密度数据

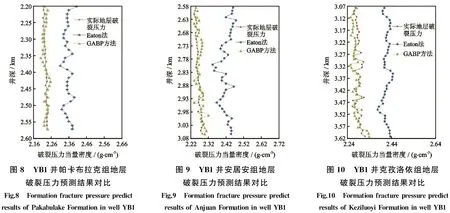
模型的预测误差约为3.5%，而Eaton法的预测误差则达到约10%。由此可以得出：遗传算法优化BP神经网络预测地层破裂压力要比常规预测方法更为准确，而且其结果不受地质构造条件的影响，且所用到的数据都很容易得到，相对而言，其适用性更为广泛。

4 结 论

(1)遗传算法优化BP神经网络克服了标准BP神经网络不稳定性和收敛速度慢的缺点，在保证计算速度的同时，实现了地层破裂压力的高精度预测。

(2)基于遗传算法优化BP神经网络的地层破裂压力预测模型考虑了地层深度、地层孔隙压力和岩石密度等主要影响因素，与Eaton法等其他常规预测方法相比，该方法不受地质构造条件影响，而且所采用数据容易得到，预测精度更高，因此其具有很好的适用性和可靠性。

(3)GABP预测模型是基于区域地质数据建立的，因此其应用范围仅限于相邻地区的邻井地层破裂压力预测，未来通用预测方法的研究还需要根据测井数据分析、区域钻井经验和压裂测试等多方面工作进行探索。

[1] 周拿云，杨兆中.地层破裂压力预测技术综述[J].重庆科技学院学报:自然科学版，2011，13(1):36-38. ZHOU Na-yun，YANG Zhao-zhong.Overview on pressure prediction of formation fracture[J].Journal of Chongqing University of Science and Technology:Natural Science Edition，2011，13(1):36-38.

[2] 聂采军，赵军.地层破裂压力测井预测的统计模式研究[J].天然气地球科学，2004，15(6):633-636. NIE Cai-jun,ZHAO Jun.Study on statistical model of predicting formation fracture pressuure using logging data[J].Natural Gas Geoscience,2004，15(6):633-636.

[3] 李敏，练章华.岩石力学参数试验与地层破裂压力预测研究[J].石油钻采工艺，2009，31(5):15-18. LI Min,LIAN Zhang-hua.Rock mechanical parametric experiments and the research of formation fracture pressure prediction[J].Oil Drilling & Production Technology,2009，31(5):15-18.

[4] 史峰，王小川.MATLAB神经网络30个案例分析[M].北京：北京航空航天大学出版社，2011:21-25.

[5] 李孝忠，张有伟.改进自适应遗传算法在 BP 神经网络学习中的应用[J].天津科技大学学报，2010，25(4):64-67. LI Xiao-zhong,ZHANG You-wei.Application of improvement self-adaptation genetic algorithm in BP neural network learning[J].Journal of Tianjin University of Science & Technology,2010，25(4):64-67.

[6] 田旭光，宋彤.结合遗传算法优化BP神经网络的结构和参数[J].计算机应用与软件，2004，21(6):69-71. TIAN Xu-guang,SONG Tong.Optimizing the structure and parameters of BP nuural network based on genetic algorithm[J].Computer Applications and Software,2004，21(6):69-71.

[7] 夏宏泉，张元泽.碳酸盐岩地层破裂压力的测井预测研究[J].天然气工业，2004，24(8):32-35. XIA Hong-quan,ZHANG Yuan-ze.Log predicyion of carbonate formation breakdown pressure[J].Natural Gas Industry,2004，24(8):32-35.

[8] 姜子昂，张永红.南东部地区阳新统的地层破裂压力预测[J].天然气工业，1994，14(2):44-47. JIANG Zi-ang,ZHANG Yong-hong.Forecasting fracture pressure in strate of Yangxin series in the eastern area of south Sichuan[J].Natural Gas Industry,1994，14(2):44-47.

[9] 易浩，白彬珍.玉北地区深井快速钻井技术[J].石油钻探技术，2011，39(6):27-30. YI Hao,BAI Bin-zhen.Faster drilling technology in Yubei area[J].Petroleum Drilling Techniques,2011，39(6):27-30.

责任编辑：张新宝

2014-10-31

中国石化“十二五”重点信息化项目“石油工程决策支持系统研究”(编号：G11-MM-2011-080)

李昌盛(1985-)，男，工程师，主要从事地层压力预测及优化钻井研究。E-mail：lichangsheng005@163.com

1673-064X(2015)05-0075-05

TE

A