交通动态路网模型与能耗最优路径诱导

张程程，康维新

哈尔滨工程大学信息与通信工程学院，黑龙江哈尔滨150001

交通动态路网模型与能耗最优路径诱导

张程程，康维新

哈尔滨工程大学信息与通信工程学院，黑龙江哈尔滨150001

针对智能交通诱导中出行者路径选择以及汽车能耗问题，对路网模型及能耗最优路径进行了研究。在传统图论方法基础上建立动态路网模型，细化路段和交叉口处的动态信息，加入交叉口处排队车辆数及排队等待时间;并分别计算路段和交叉口处匀速及怠速时的汽车行驶能耗，进而建立了能耗最优路径诱导模型;再将能耗融入到蚁群算法的信息素更新规则中，用改进后的蚁群算法进行实验仿真。仿真结果验证了动态路网模型的有效性，得到的能耗最优路径能够有效减少行程内10%左右的能耗，达到节能减排的目的，符合实际需求。

智能交通诱导;动态路网模型;动态交通信息;能耗最优路径;改进蚁群算法

网络出版地址: http://www.cnki.net/kcms/detail/23.1191.U.20150727.1031.006.html

交通拥堵、汽车尾气问题一直都是智能交通的研究重点，怎样选择便捷路径行驶以减少汽车能耗已成为出行者日益关注的问题。生态智能交通［1］的提出为交通诱导与节能减排提供了一个新的发展方向，能够有效地降低汽车能耗。

国内外学者在有关交通诱导的路网建模、最优路径以及汽车排放等方面进行了很多的研究。在构建路网模型方面，曹政才等［2］建立了以道路为基本元素的RBM模型，但如果交通信息量大则会增加计算量。Demir等［3］构建一种聚类超图模型，并通过把基于节点的数据存储方式转化为基于路段的数据存储方式，减少路网数据的存储量;宋青等人［4］建立了一个基于小区的大规模分层图论路网模型，提出新型分层路由算法提高了空间搜索精度。文献［5］将静态路网与动态信息结合起来建立了动静态广义路网模型。文献［6］提出了考虑用户均衡的新型动态模型，解决静态和动态交通分配问题。以上的路网模型，都把交叉口当作路段的一部分。但是实际上，交叉口处的信息是不可忽略的。在最优路径方面，文献［7］提出了基于智能优化搜索理论和人工免疫系统的最优搜索算法，实现路径诱导。文献［8］在博弈论基础上，建立了考虑广义出行费用的路径选择模型。文献［9-11］针对蚁群算法易陷入局部最优解的问题对蚁群算法进行了改进，实现有效的路径搜索。另外，李世武等［12］从排放角度确定了最佳的信号配时优化方案。文献［13］研究了道路等级以及行车速度对排放的不同影响。由以上研究可以看出，若从路网模型和能耗的角度进行交通诱导路径寻优，对实现交通节能减排具有重要的现实意义。

文中在传统图论的基础上，构建出动态路网模型，细化交叉口和路段的动态信息。对交叉口和路段的行驶能耗进行计算并得出能耗最优路径诱导模型，应用改进蚁群算法对模型进行求解，得出能耗最优路径。

1　动态路网模型的构建

1.1动态交通路网模型

城市交通路网复杂多变，从总体上看，都是由道路交叉口和路段相互连接而成的。可以用图论法对交通路网进行拓扑化抽象，图论中的节点及弧段分别与实际路网的交叉口及路段一一对应，并且对弧段进行赋权描述。

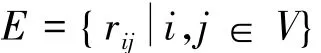
1.2路网中动态交通信息

实际路网中，影响交通网络通行能力的交通因素分别发生在交叉口和路段上。下面分别对交叉口和路段相关信息进行描述。

信号交叉口延误是由于交叉口处信号控制引起交通流间断而损失的车辆行驶时间，文中以十字交叉路口为例。根据质点排队模型，当交叉口驶出流量大于出口通行能力时，则在该处将出现点排队。此处，可以简化交叉口处的动态因素，排队时间的计算仅考虑路口排队车辆数，可以更直观、简便地反映实际路网，减少计算量。

交叉口排队延误时间与排队车辆数关系为

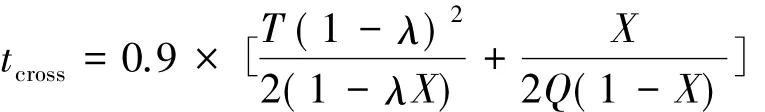
式中: tcross为交叉口排队延误时间，T为周期长度，λ为交叉口信绿比，X为交叉口饱和度，Q为交叉口交通量。饱和度X表示为

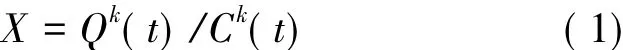
式(1)中: Qk(t)为t时刻的排队车辆，veh; Ck(t)为t时刻交叉口最大负荷，veh。

城市交通路段上的动态因素相对复杂，其中单位时间内的交通量表现为动态性和随机性;通行能力则为交通规定运行特征下的最大流量，表现为相对稳定性和规律性;行车速度、车流密度在交通状态上也表现出敏感性。下面将对主要的路段动态信息进行描述。

由交通流理论可知，交通量、速度和密度3个参数之间的关系为

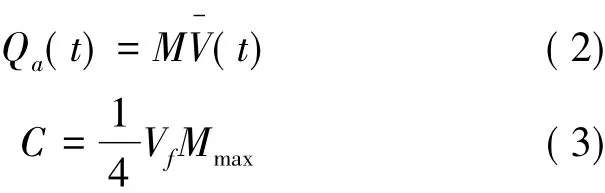
式(2)中: Qa(t)为路段的车流量，M为路段车流密度，(t)为路段行车速度。式(3)中: C为路段的通行能力，Vf为自由流行驶时的行车速度，Mmax为最大车流密度。

设定某路段的长度为la，则有

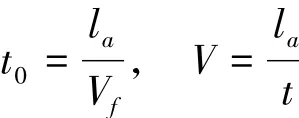
式中t0为自由流状态下经过路段a的所需的时间。

路段流量与路段行驶所需时间的关系为

路段的行程时间是影响路径寻优的一个重要指标，而道路的拥堵的判定指标也备受关注。交通拥堵指数(traffic performance index，TPI)是北京市首创的综合反映道路网畅通或拥堵的概念性数值。TPI分成5个等级，取值用0～10之间的正整数来表示，数值越高，拥堵越严重。

为了简化计算，文中在此基础上简化了TPI等级，如式(4)所示，路段拥挤程度值为

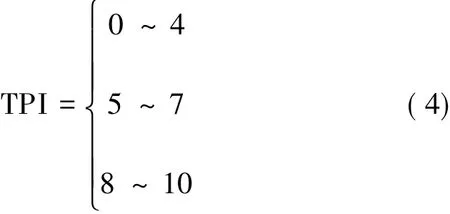
在进行交通状态分析时，可取TPI的不同值来判断路段的拥挤程度，对交通状态进行评价。此外，影响路段通行能力还有另外一个动态信息，如当遇到修路、雨雪天气导致的封路时，这个路段就为限行路段，这个路段的耗费可以设置为无穷大。

1.3车辆行驶能耗

城市道路上车辆行驶的能耗分为2部分，主要是在路段上以及交叉口红绿灯时的能耗。车辆行驶能耗的特点是，车辆从怠速到匀速行驶过程中能耗相对匀速行驶较大。在有信号控制的交叉口上，车辆一般有2种运动状态:一是车辆到达交叉口时遇到红灯和拥堵状态需要排队等待时，车辆必须怠速再启动通过交叉口。二是车辆到达交叉口时信号为绿灯，车辆匀速通过交叉口，其能耗量近似按路段能耗计算。

按照不同车型，能耗率也是不同的，见表1。

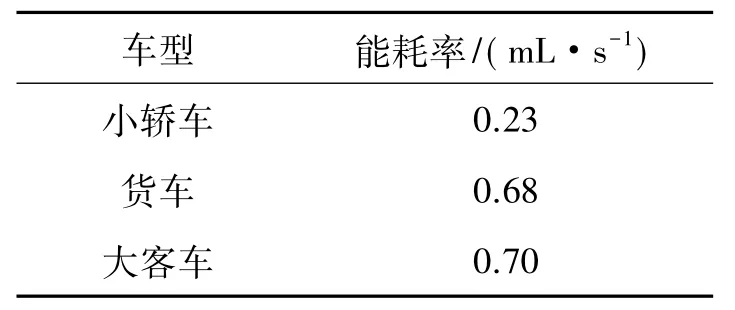
表1　不同车型能耗率

文中定义式(5)计算能耗:

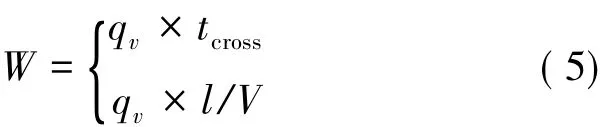
式中: qv为油耗率，也可称作怠速因子; l为路段长度; V为行驶速度。

2　能耗最优路径诱导模型及改进蚁群算法

2.1能耗最优路径诱导模型

交通网络中最短路径问题一直都是研究的热点。但是由于交通信息的不断变化，最短路径已经不能够作为最合理路径的标准。最优路径将从距离最短、时间最少和能耗最短等角度来诠释。

结合上述所建立的动态路网模型，建立了最优路径诱导模型，也可称作耗费最小模型。设Lmin为车辆最小耗费所经过的路径，rij、ri、rj为所经过的路段和交叉口。这是一个组合优化问题，可用式(6)的数学模型来表示:

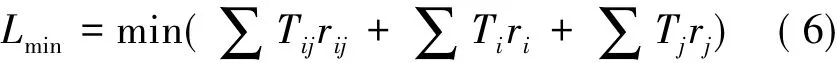
式中:若最优路径经过节点或路段，则rij、ri、rj取值为1，反之，取0。

根据车辆行驶的能耗公式，可得出能耗最优路径诱导模型:

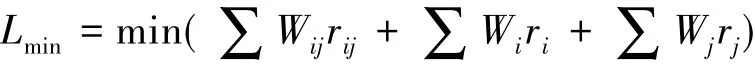
式中: Wij为绿灯或路段上的能耗，Wi、Wj为交叉口处红灯或拥堵时的能耗。同理，当计算距离最短和时间最少路径时，只需将式(6)中的耗费值改成相应的距离和时间。

2.2改进蚁群算法

蚁群算法作为一种启发式算法，常用在智能交通中的路径诱导方面。它是一种仿生学算法，通过模拟蚂蚁觅食的过程，将其应用到路径搜索过程中，并及时对外界的信息做出响应得到最优路径。影响蚁群算法的核心因素有2个，一个是节点间转移概率的计算策略，另一个是信息素更新规则。而传统蚁群算法在路径寻优过程中，搜索效率低并易陷入局部最优，搜索结果不稳定。

为了提高算法效率，使蚁群算法更加适应外界信息的变化，得到最优路径，文中分别在转移概率选择和信息素更新规则上进行改进。

在蚁群算法中，β为期望启发因子。外界的动态信息影响蚂蚁转移概率中的β，所以这里β不再是一个固定值，它与交通道路的拥堵指数有关，令β=TPI，当TPI越小时，道路越畅通，此时蚂蚁倾向于选择信息素浓度较高的地方。设m为蚁群中蚂蚁的数量，τij(t)相邻2个节点间的信息素量，为了提高算法的效率，直接去遍历和节点i相连接的节点，这里Vk={和i直接相连的节点}，则转移概率为

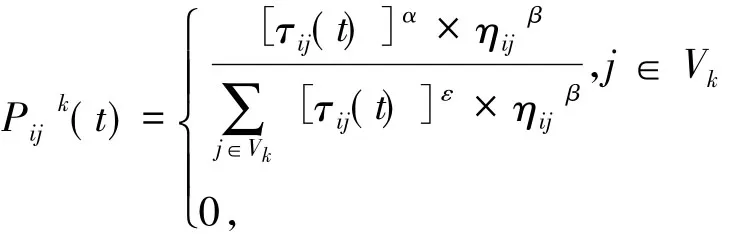
否则式中:α为信息启发因子，ηij=1/dij为能见度启发因子。

在信息素更新规则上，蚂蚁每走一步后所经过的路径上的信息素要进行挥发，如式(7)所示。

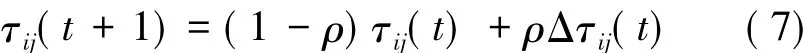
式中:ρ为信息素的挥发程度，Δτij(t)为路径上的信息素增量。局部更新可以有效地避免蚂蚁收敛于同一条路径。

而蚂蚁每经过一次循环后时，得到的最优解所经过的路径上的信息素要增强，而非最优解的路径上的信息素要减弱。将更新因子引入全局更新中，按照式(8)更新信息素:

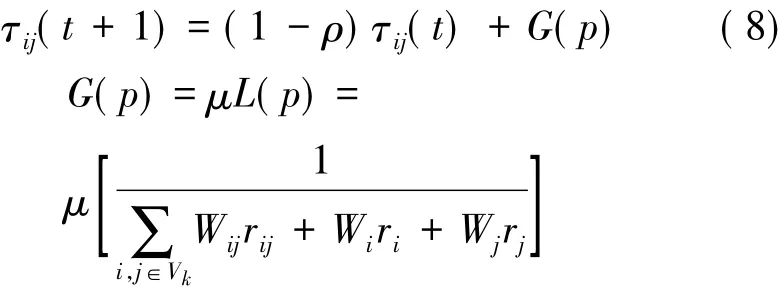
式中: G(p)为更新因子，是能耗的函数，μ为正实数，表示此路径的相对重要性，L(p)为能耗估计。若蚂蚁所选路径上的能耗相对较小，则更新好该路径上信息素将增强，其他蚂蚁选择此路径的几率相对增大。通过上述更新后的信息素不仅可以反映各路径和节点的权值变化，也反映出最优路径的选择情况。

算法的具体步骤如下。

1)初始化各路径上的信息素都为一常数;蚂蚁数目为m;并将m只蚂蚁放在起点处。

2)在t时刻每只蚂蚁按式(6)所示的转移概率选择下一节点。

3)到达下一节点后，用式(7)进行信息素的局部更新。

4)判断节点j是否为目的节点，若为目的节点则保存蚂蚁走过的路径。若不是目的节点，则返回步骤2)。

5)当m只蚂蚁全部迭代完后，则将各路径上的信息素按式(8)进行全局更新。并将每只蚂蚁搜索到的最优路径进行比较，得出全局最优路径。

3　仿真实验

城市路网建设错综复杂，文中借助VS2010软件平台，对真实道路网应用改进的图论模型进行网格化抽象。图1为仿真路网环境，其中黑色节点部分为交叉口，连接节点之间的连线为路段，每条路段间距离不同，示意图中标注了相应静态距离。下面将从能耗角度对最优路径进行模拟验证。首先进行初始化设置，设上路车辆均为小轿车，标准乘载，能耗率qv为0.23 mL·s－1，假设此时的路网正处于早高峰时段，局部车流相对缓慢，交通状况实时变化。此时在路口n5、n7处出现轻微拥堵;在n11、n22交叉口处排队车辆数较多，车行缓慢;其他路段相对较畅通。此时，车辆以n1为起点，终点为n19。

图1　仿真路网示意

算法的参数设置为:车辆数量m=30;量子位数为2;概率参数q0=0.5;挥发系数ρ=0.7;α=0.5; β=0.5;最大迭代次数为400。在动态路网下应用改进后路径寻优算法得出的路径为n1－n2－n6－n10－n14－n18－n19，行车距离为19.5 km，能耗为0.49 L。而在静态路网下，车辆选择的是距离最短路径为n1－n5－n9－n10－n11－n15－n19，虽然走过路程为18.5 km，但是由于路口拥堵而造成等待时间延长，耗油量为0.55 L。路径仿真结果如图2。

图2　路径仿真结果

选择2组起点终点，在静态和动态路网下有不同路径，具体数据见表2、3。

表2　不同起终点的能耗最优路径

表3　不同路径的能耗量对比

分析上面的路径表可知，尽管在静态路网下能使行驶距离减少，但是却在行驶过程中增加了等待时间，增大了能耗，静态路网不能及时的对路网上的动态信息做出及时响应。而在动态路网中，距离不一定最短，但能够避开交叉口拥堵，减少了行程内怠速等待，根据表3所示，在动态路网下的能耗相对减少，比较符合出行者的需求。图3为改进蚁群算法下能耗最优解收敛图，在图中可以看出，未改进的蚁群算法在搜索过程中易出现早熟现象，收敛速度也较慢，未搜索到全局最优解。而改进蚁群算法可以有效避免局部最优现象的出现，提高了收敛速度。

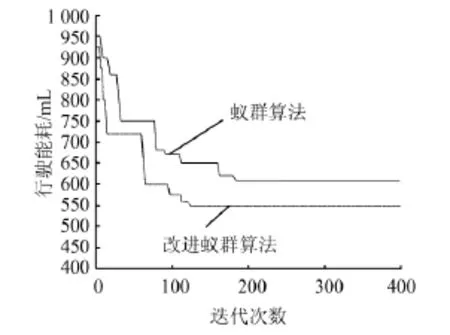
图3　改进蚁群算法下的能耗最优解收敛

4　结束语

文中针对实时变化的交通路况，在图论基础上建立的动态路网模型综合考虑了交叉口和路段的动态信息，进而推导出能耗最优路径诱导模型;再针对蚂蚁状态转移概率和信息素更新规则方面对蚁群算法进行改进，改进后的蚁群算法可以有效地避免局部最优解，提高了算法的效率;由不同起终点得出的能耗最优路径可以有效地节省能耗，符合实际需求;也为今后研究交通诱导中的系统综合最优提供了基础，具有现实意义。

［1］朱昊，陶晨亮，赵方.发展生态型智能交通系统的建议［J］.交通与运输，2013，29(3) : 21-22.

［2］曹政才，韩丁富，乔非.基于新型路网模型的路径寻优方法研究［J］.电子学报，2012，40(4) : 756-761.

［3］DEMIR E，AYKANAT C，CAMBAZOGLU B B.A linkbased storage scheme for efficient aggregate query processing on clustered road networks［J］.Information Systems，2010，35(1) : 75-93.

［4］SONG Qing，WANG Xiaofan.Efficient routing on large road networks using hierarchical communities［J］.IEEE Transactions on Intelligent Transportation Systems，2011(12) : 132-140.

［5］YANG Yuhong，HAN Xiaowei，YUAN Zhonghu.A model of dynamic traffic road network［J］.IERI Procedia，2012 (13) : 46-51.

［6］JIN Wenlong.A dynamical system model of the traffic assignment problem［J］.Transportation Research Part B，2006，41 (1) : 32-48.

［7］YANG Licai，LIN Jie，WANG Dewei，et al.Dynamic route guidance algorithm based on artificial immune system［J］.Journal Of Control Theory and Applications，2007，5 (4) : 385-390.

［8］FENG Yuqin，LENG Junqiang，XIE Zhongyu，et al.Route choice model considering generalized travel cost based on game theory［J］.Mathematical Problems in Engineering，2013(1) : 1-5.

［9］LIU Zhishuo.SHEN Jinsheng，CHAI Yueting.Hybrid multiple ant colonies algorithm for capacitated vehicle routing problem［J］.Journal of System Simulation，2007，19(15) : 3513-3520.

［10］SONG Jinjuan，BAI Yanping.An improved ant colony algorithm and its application in optimal routing problem［J］.Journal of Measurement Science and Instrumentation，2013，4(1) : 23-29.

［11］GAN Rongwei，GUO Qingshun，CHANG Huiyou，et al.Improved ant colony optimization algorithm for the traveling salesman problems［J］.Journal of Systems Engineering and Electronics，2010(2) : 329-333.

［12］李世武，王云鹏，付建萍，等.基于车辆排放的城市道路交叉口信号配时优化仿真［J］.吉林大学学报:工学版，2007，37(6) : 1268-1272.

［13］王云鹏，郭栋，隗海林，等.城市分等级道路车辆运行速度对排放的影响［J］.哈尔滨工业大学学报，2009，41 (7) : 110-114.

Traffic dynamic road network model and energy consumption optimal route guidance

ZHANG Chengcheng，KANG Weixin

College of Information and Communication Engineering，Harbin Engineering University，Harbin150001，China

To solve the problem of the traveler route choice and energy consumption in intelligent traffic route guidance，a dynamic road network model was established based on the traditional graph theory methods.This model described the dynamic information of road segments and intersections，with the relationship between the number of queuing vehicles and the queue waiting time.The energy consumptions of vehicles moving at even and idle speed on the roads and intersections was calculated，respectively.Then the energy consumption optimal route guidance model was suggested，and the energy consumption was integrated to the pheromone updating rule of an ant colony algorithm; then simulation was carried out by the improved ant colony algorithm.The simulation results show that the dynamic road network model is effective.In addition，the derived optimum route of energy consumption can effectively reduce the vehicle energy consumption in the travel，which saves about 10% energy compared with the static road network.

intelligent traffic guidance; dynamic road network model; dynamic traffic information; energy consumption optimal route; improved ant colony algorithm

TP301.6

A

1009-671X(2015) 04-043-05

10.3969/j.issn.1009-671X.201412001

2014-12-01.网络出版日期: 2015-07-27.

黑龙江省交通运输资助项目(G084812068).

张程程(1987-)，女，硕士研究生;康维新(1963-)，男，教授，博士.

康维新，E-mail: kangweixin@hrbeu.edu.cn.