一种基于编队中心的目标跟踪算法

郭荣华，李晓，李耀炜，周颖

（1.中国洛阳电子装备试验中心，洛阳 471099；2.中国光电技术发展中心，洛阳 471099）

一种基于编队中心的目标跟踪算法

郭荣华1，李晓2，李耀炜1，周颖1

（1.中国洛阳电子装备试验中心，洛阳 471099；2.中国光电技术发展中心，洛阳 471099）

摘 要：提出了一种将多目标作为一个编队进行整体跟踪的方法，包括编队生成、编队分离、编队合批和编队跟踪维持，解决了多目标的整体跟踪问题。结合交互式多模型粒子滤波算法（IMM-UPF），在实践中，有效地减轻了计算负担，节约了系统资源，具有实用性。

关键词：编队；目标跟踪；编队中心；IMM-UPF

*项目简介：自然科学基金（61303061）。

本文引用格式：郭荣华，李晓，李耀炜，等.一种基于编队中心的目标跟踪算法[J].新型工业化，2015，5(4)：40-47

1　引言

当多个目标以编队方式进行机动时，利用编队进行跟踪控制可以减少系统代价，增加系统的鲁棒性和效率，具有较强的重构能力和结构灵活性。编队控制有着广泛的应用，比如，危险环境中的安全巡逻、搜救，军事任务中为完成区域覆盖和侦察的任务编队，多颗卫星协同有助于节约能源和扩展其感知能力[1-2]。对于地面编队目标（包括军事装备、民用车辆等）跟踪，由于地面目标距离相对较近、运动的不确定性及回波环境的复杂性，相对于空中目标跟踪，其问题尤为突出。Bar-Shalom等[3-4]提出了将一个“聚”作为一个群对待，做了大量的研究工作。Taenzer[5]在“质心”跟踪的基础上，提出了编队跟踪起始、维持和分离的一些方法。近年来，粒子滤波由于其滤波精度高的优点，以及与交互式多模型的结合使用，为编队目标跟踪提供了一种可行的解决途径[6-8]。

针对地面编队目标机动性强、干扰大的特点，给出了编队生成、编队分离、编队合批以及编队跟踪维持的逻辑处理方法，并与交互式多模型粒子滤波算法（IMM-UPF）结合，提出了一种基于编队几何中心的目标跟踪算法，并在工程中进行了实践。

2　编队目标跟踪逻辑处理方法

2.1编队定义

判定能否将多目标作为一个编队进行考虑，有如下两种规则：

规则1：如果在连续时序内，多个目标距离相近，在任一时刻具有相同的速率和运动方向，也即它们的空间结构稳定，就把这几个目标称为一个编队。

规则2：如果在连续时序内，多个目标“聚”在一块，与其它目标距离相距较远，就把这样的“聚”称为一个编队。

规则1的条件约束较强，规则2的定义比较宽泛。编队跟踪算法中采用规则1的定义。

2.2编队维持

编队目标跟踪维持可以选择编队最小外接矩形、最小外接圆或最小闭包的几何中心，且采用几何中心跟踪法对编队进行跟踪维持。在编队合批后，对编队几何中心进行修正操作。因为当新目标加入后，该编队目标的关联区域就会产生变化。如果继续使用原有的几何中心，就会出现对新编队目标跟踪不准确的问题。因此，编队进行合批后，必须对原有的编队几何中心进行重新修正。对于编队目标最小外接矩形，长与宽始终分别与笛卡尔坐标系的X轴与Y轴平行。

2.2.1目标预测的最小外接矩形的确定

对于三个以上的目标，无论多个目标是处于一条直线上或不在一条直线上，处理方法是一样的。这里考虑一般情况，假设有N个目标组成一个编队，如图1所示。N个目标的二维笛卡尔坐标位置向量分别记为：T1(x1, y1), T2(x2, y2), , Ti(xi, yi), , TN(xN, yN).

设目标预测最小外接矩形的四个顶点分别为A(xa, ya)、B(xb, yb)、C(xc, yc)和D(xd, yd)，矩形几何中心为O(xO, yO)，则有

2.2.2确定目标预测最小外接矩形的中心

矩形几何中心点O的位置向量可以根据矩形四个顶点的向量确定

2.2.3建立矩形中心与编队中各目标的对应关系

也即Ti→O: [Δxi, Δyi]。因此，整个编队中的所有目标与中心O的对应关系可以表示为

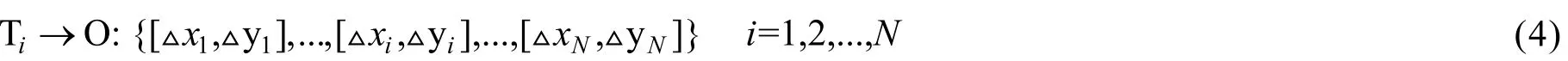
2.2.4由坐标差对求下一时刻的各目标预测位置向量

注意，记录坐标差对[Δxi, Δyi]比记录OTi之间的距离和角度更方便，计算更直接、快速。

2.2.5目标量测处理

对于编队目标的量测，与编队目标预测一样，首先确定量测的最小外接矩形及其中心，然后建立各量测与其矩形中心的对应关系。其演化过程如图3所示。

图1.目标预测与量测最小外接矩形及其几何中心的确定Fig.1 Determine the minimum enclosing rectangle of target predicted and measurement positions, and their geometric centre

图2　编队预测中心演化Fig.2 The evolution of the prediction centre of a formation

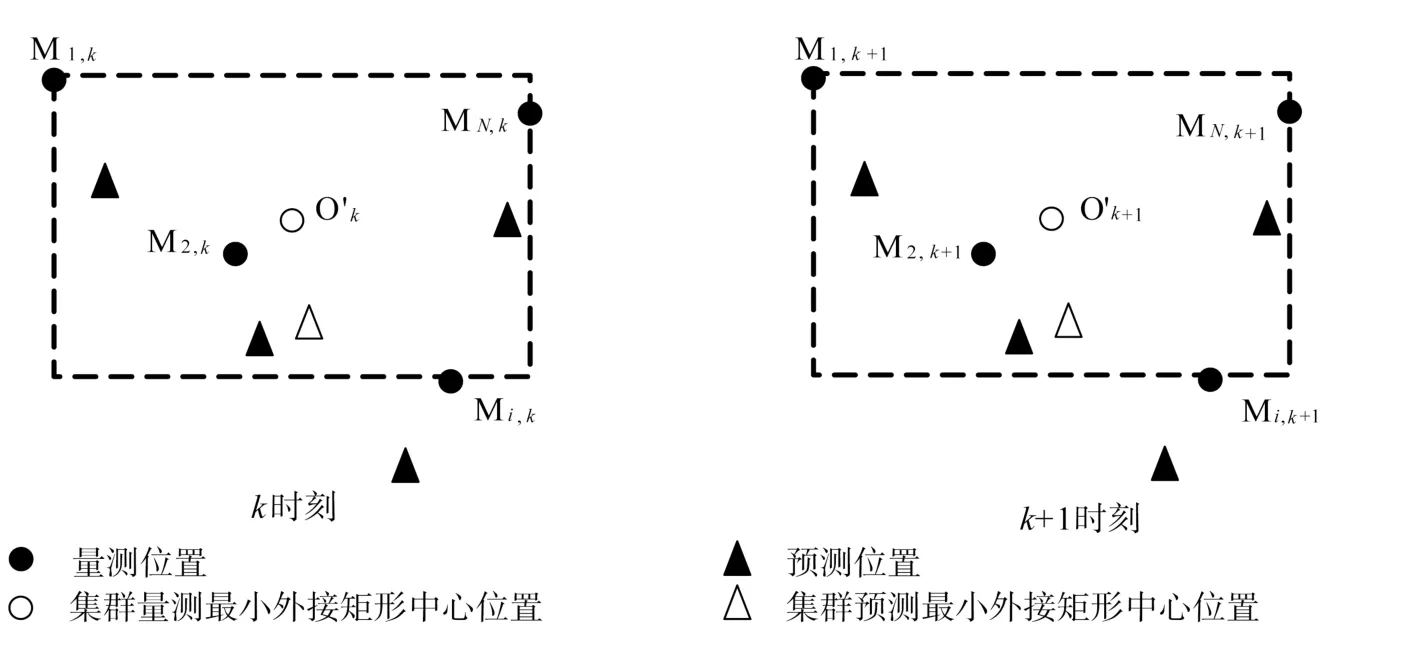
图3　编队量测几何中心演化Fig.3 The evolution of the measurement centre of a formation

3　编队分离和合批

编队的分离和合批都属于编队逻辑处理的范畴，为了方便描述编队分离和合批算法原理，一些符号定义如表1和图4所示。

表1　一些符号定义Table 1.Definitions of some symbols

3.1编队的分离算法

(1) 如果Fj(di)＞Fj(r)且Tj(di)＜Tj(r)，将目标i从编队中分离出去，成为新目标，参与合批。

(2) 如果编队中的目标外推跟踪次数超出设定值（即无关计数器NoRelationCounter(i) ≥ m）或者Tj(di)＞Tj(r)，将该目标从编队中分离并且丢弃。

图4　编队分离和合批符号定义示意Fig.4 The Representations of symbols on formation separating and combining

3.2编队的合批算法

(1) 初始化，每个编队只有1个目标或者跟踪指定的编队目标。

(2) 如果发现新目标，计算新目标与所有跟踪编队中心最近的距离min{Fj*(dl)}。若min{Fj*(dl)}＜Fj(r)，则将该目标添加到距离最近的编队；否则，把该目标作为1个新的编队，新目标的产生由滑动窗口方法确定或者由编队的分离过程产生。

4　FC-IMM-UPF算法

由于编队的空间结构相对稳定，这里采用基于群几何中心的IMM-UPF算法（FC-IMM-UPF）。算法原理描述如下（从k-1时刻到k时刻的一次循环）。

1.计算编队的中心、所有目标与编队中心的偏移量和量测的中心。

xi,k表示编队中k时刻目标i的状态估计向量，编队几何中心的状态估计与状态预测向量分别用xk和xk+1|k表示；zi,k表示编队中k时刻目标i的量测向量，编队几何中心的量测与量测预测向量分别用zk和zk+1|k表示；Δxi,k是k时刻编队中目标i相对于群几何中心的偏移量。

(1) 根据式(1)和式(2)，k-1时刻的编队目标中心状态估计为xk-1，计算编队目标中心的状态一步预测xk|k-1。

(2) 根据式(3)和式(4)，计算编队中k-1时刻目标i相对于群几何中心的偏移量Δxi,k -1。

(3) 根据量测zi,k，计算k时刻编队目标量测中心向量zk。

2.更新k时刻编队的中心、所有目标的状态更新及一步预测。

5　仿真与分析

将FC-IMM-UPF算法用于编队状态的跟踪维持、新目标增加（编队合批）和目标丢失（编队分离）过程中，利用编队跟踪方式和多目标跟踪方式，分别对一个跟踪实例进行处理，分析编队中目标个数对不同跟踪方式的影响。目标运动模型使用CV（常速模型1）和CT（转弯模型2）模型进行模拟。采用建议的量测模型获得量测数据，采样时间T=1s。

模型1（CV）：

模型2（CT）：

量测模型：

5.1测试用例

1.想定。编队中的目标从（0m, 0m）处开始，以20m/s的速率作蛇形机动，整个机动时间持续125s，采样间隔为T=1s。编队起始时，由四个目标成菱形组成，具有相同的速度和运动方向。编队目标真实运动航迹和局部放大图如图5(a)和(b)所示。当编队目标机动至20s时，新目标（目标5）出现，并加入到编队中，如图5(c)所示。当编队目标机动至100s时，目标5从编队中消失，如图5 (d)所示。

图5　编队目标运动真实航迹Fig.5 Formation target movement real track

2.仿真条件。模式变迁矩阵为

对于FC-IMM-UPF算法，粒子数N=200，每个模型粒子数设为100。

5.2性能分析

对于此想定，在不同的噪声条件下，对FC-IMM-UPF算法进行了100次蒙特卡罗仿真。

1.估计精度或RMSE性能。利用FC-IMM-UPF算法对编队目标进行跟踪，得到编队中心估计和局部放大图如图6(a)和(b)所示。可见，该算法能够对编队目标进行有效跟踪，当新目标加入和目标离开编队时，算法也可以对编队中心迅速进行跟踪处理。在弧顶处，状态估计略有偏差，不过没有发生滤波发散现象，编队目标跟踪比较正常。

2.计算时间复杂度。为了分析地面机动目标跟踪中编队目标个数与所采取的跟踪方式（编队目标跟踪和多目标跟踪）在时间复杂度方面的影响，将想定中的编队目标个数设定为10个、20个、30个，分别计算目标跟踪处理的单步计算时间，如表2所示。编队跟踪采用编队目标跟踪处理方法和IMM-UPF算法，多目标跟踪算法采用IMM-UPF算法和NNDA数据关联算法[9]。从表2可以看出，随着编队中目标个数的增加，以编队方式进行跟踪的效率越高，相对多目标跟踪方式，优势越明显。

图6　编队中心状态估计Fig.6 The estimation of formation centre

表2　编队目标个数与跟踪方式的计算时间对比Table 2.A comparison of computing time for the number of targets in a formation and tracking mode

6　结论

采用群几何中心跟踪算法在工程实践中，能够实现对多目标的整体跟踪，当新目标加入和目标丢失时，可以正常跟踪处理，解决了多目标的整体跟踪问题，从而减少了计算量，节约了系统资源，因此具有实用性。

参考文献:

[1]Do KD.Formation tracking control of unicycle-type mobile robots[C].2007 IEEE International Conference on Robotics and Automation, 2005: 2391-2396.

[2]Scharf DP, Hadaegh FY, Ploen SR.A Survey of Spacecraft Formation Flying Guidance and Control (Part 11): Control[C].Proceedings of the 2004 American Control Conference, 2004, 4: 2976-2985.

[3]Bar-Shalom Y, Li X R.Multi target-multi sensor tracking: principles and techniques[M].New Orleans: University of New Orleans, 1995.

[4]Bar-Shalom Y, Li X R, Kirubarajan T.Estimation with Applications to Tracking and Navigation: Theory, Algorithm and Software[M].New York: Wiley, 2001.

[5]Taenzer E.Tracking multiple targets simultaneously with a phased array radar[J].IEEE Transactions on Aerospace and Electronic Systems.1980, 16(5): 604-614.

[6]Ronghua Guo, Zheng Qin.An unscented particle filter for ground maneuvering target tracking[J].Journal of Zhejiang University SCIENCE-A, 2007, 8(10): 1588-1595.

[7]Kwangjae S, Hwangnam K.Bayesian navigation system with particle filtering and dead reckoning in urban canyon environments[C].The 9th Annual IEEE Communications Society Conference on Sensor, Mesh and Ad Hoc Communications and Networks (SECON).2012: 73-75.

[8]Guo R H, Qin Z, Li G B, Li X N.An IMM-AUPF algorithm with a re-sampling controller[J].Journal of Tsinghua University, 2010, 50(4): 539-542.

[9]Bar-Shalom Y.Tracking methods in a multitarget environment[J].IEEE Transactions on Automatic Control, 1978, 23: 618-626.

A Center-based Formation Target Tracking Algorithm

GUO Ronghua1, LI Xiao2, LI Yaowei1, ZHOU Ying1
(1.electronic equipment test center satellite navigation laboratory, Luoyang 471099, China; 2.China Opto-Electro Technology Center, Luoyang 471099, China)

Abstract:Based on the formation center (FC), a logical method to formation target tracking, which include formation initiation, formation separation, formation merging and formation updating, is proposed according to the kinetics of formation moving.The method addresses the tracking problem of taking multi-targets tracking as a whole.Integrating with the IMM-UPF, a FC-based interacting multiple model unscented particle filter (FC-IMM-UPF) is presented.Simulation shows that the FC-IMM-UPF algorithm improves the estimating accuracy and reduces the computational complexity.

Keywords：formation; target tracking; formation center (FC); IMM-UPF

DOI：10.3969/j.issn.2095-6649.2015.04.06

作者简介：郭荣华(1972-)，男，湖北，副研究员，博士，主要研究方向：信息安全。

Citation: GUO Ronghua, Li Xiao, Li Yaowei, et al..A Center-based Formation Target Tracking Algorithm [J].The Journal of New Industrialization, 2015, 5(4): 40‒47.