管壁均匀密集加糙圆管流的新总流机械能方程及流动数值模拟

潘文浩，刘士和

（武汉大学 水利水电学院，湖北 武汉 430072）

管壁均匀密集加糙圆管流的新总流机械能方程及流动数值模拟

潘文浩，刘士和

（武汉大学 水利水电学院，湖北 武汉 430072）

能量（机械能）方程是水力学的理论基础；能量损失（机械能损失）的计算既是水力学乃至工程流体力学的主要研究内容之一，也是工程实际中颇为关注的问题。以往水力学中的能量方程系以重力场中理想不可压缩流体的伯努利方程为基础而得到，其既不能直接反映紊动对流动的作用，能量损失也无明确的表达式。本文在我们现有研究工作基础上，通过理论分析与数值模拟，得到如下成果：（1）构建了管壁均匀密集加糙圆管流的新总流机械能方程；（2）通过数值模拟，对管壁均匀密集加糙圆管流的机械能损失及其构成进行了研究。构建的方程包含了紊动的作用；研究成果表明，均匀密集加糙圆管流总流机械能损失与雷诺数及管壁光滑度有关，且可分解为与时均流速梯度相关的损失及与紊动耗散相关的损失两部分。

圆管流；均匀密集加糙；机械能损失；紊流

1 研究背景

能量方程（机械能方程）是水力学的理论基础之一，能量损失的确定既是水力学及工程流体力学的重要内容，也是工程实际中颇为关注的问题。实际工程中管道的管壁总有一定的绝对粗糙度，因此，研究管壁均匀密集加糙条件下的总流机械能方程及机械能损失具有较高的理论意义与工程价值。

目前水力学中的总流能量方程是以重力场中理想不可压缩流体恒定流沿流线的伯努利方程为基础，通过修正而得到的，其思路及推导步骤如下：（1）引入微元流、总流、过水断面等概念，将总流视为由众多微元流构成；（2）引入沿流线的伯努利方程描述微元流机械能的沿程变化，并在其基础上引入微元流的水头损失来反映理想水体与实际水体运动的差异；（3）将微元流的能量方程沿过水断面积分，得到实际水体的总流能量方程。从水动力学的角度来看，由此得到的总流能量方程在理论上不严谨；不能直接反映紊动对流动的作用；也无法直接给出机械能损失的表达式，因此对机械能损失不得不通过实验等方法来进行研究。自著名的尼古拉兹实验［1］以来，人们对管道的流动阻力及机械能转化与损失进行了大量的实验研究，积累了丰富的经验。Colebrook［2］对不同粗糙方式的管道阻力系数进行了实验研究，并与已有研究成果进行了比较。Brown［3］总结了管流Darcy-Weisbach公式的发展历史。McKEON等［4］对充分发展管流的阻力系数进行了实验研究，得出了统一的阻力系数关系式，与已有成果吻合较好。贺益英［5］等对弯管的局部阻力系数进行了试验研究，推荐了常用的圆弧弯管、多片组合弯管局部阻力系数经验公式。我们曾经过理论分析，对圆管与明渠中均质不可压缩液体的恒定总流建立了新的机械能方程，并对机械能损失进行过研究，解决了上述问题［6-7］，但限于讨论光滑壁面上的流动。本文通过理论分析与数值模拟，对管壁均匀密集加糙条件下圆管流的总流机械能方程与机械能损失进行了研究。

2 均匀密集加糙恒定圆管流的新总流机械能方程

考虑如图1所示的控制体V内的圆管中的恒定（系综平均意义上）流动，该控制体由相距 L的两断面 A1、A2及管壁A3所构成，以S表示由A1、A2与A3构成的控制体V的表面，以θ表示管轴线（x1轴）与水平方向的夹角，对重力场中密度为ρ的水体，其控制方程为［8］

对于粗糙管壁内的流动，由于管壁高低不平，虽然在单个粗糙元表面，流速必须为零，当在不同的断面及同一断面的不同点处，管壁的凹凸不平使流速为零的点未必在同一径向位置，通常采用理论零点位置的调整来反映管壁的粗糙效应［9］。以d表示圆管有效直径；以Δ与r′分别表示管壁的绝对粗糙度及理论零点位置与粗糙体顶部之间的距离，r′=αΔ。则在管壁A3处时均流速的边界条件变为

对式（1）在控制体V上进行积分，并利用高斯定理将相应的体积分项转化为面积分项，得到

图1 粗糙管壁上的管流示意图

式（2）中ni为表面S上沿外法线方向的单位向量；ρF表示时均压强pˉ与静压强 ps的偏差，也即。类似文献［6-7］的讨论，根据静压沿断面分布的特性，利用管壁处时均流速的边界条件及恒定流的连续方程得到

式中：g为重力速度；z、ps分别表示相应断面上的某点距离基准面（水平面）的垂向距离及相应的静压强。以A、U分别表示相应断面上的断面面积及相应的断面平均流速；以下标1、2分别表示断面A1、A2的特征量，并定义动能修正系数α1、α2分别为

我们得到

因此，如果我们定义

则式（2）可进一步简化为

式（4）即为管壁均匀密集加糙的恒定圆管流的总流机械能方程，式中hT为相应断面上动水与静水的表面力势能差，我们将其简称为动静势能差；hw表示单位时间单位重量水体由断面A1流到A2的机械能损失，由式（3c）可知其总为正值，因此，当水体由断面A1流到A2时，其机械能是减少的。式（4）与文献［8］中光滑壁面上的总流机械能方程在形式上是一致的，但在断面概化、机械能损失的计算等则有所不同。对管壁均匀密集加糙条件下的圆管恒定均匀流，注意到断面上紊动能的总耗散量与总产生量是相等的，也即，定义机械能损失系数，利用轴对称条件将式（3c）可进一步简化为λ=λ1+λ2，式中λ1、λ2分别表示相应于时均流速梯度及紊动能耗散的机械能损失系数，且有

3 管壁均匀密集加糙的圆管流的数值模拟与机械能损失计算

要用式（5）对圆管流的机械能损失进行计算分析，首先必须获得时均流场特性，下面就时均流场的获取及管壁均匀密集加糙条件下圆管流的机械能损失系数计算分析分别加以介绍。

3.1 时均流场获取

（1）控制方程与边界条件采用基于雷诺应力模式（RSM）的雷诺时均方程来描述管壁均匀密集加糙条件下圆管流运动，其控制方程详见文献［10］。边界条件为：给定进口流速等特征量；管道足够长，保证在出口处流动充分发展。将管壁附近的第一层网格布置在粗糙元顶部，其纵向时均流速为

（2）数值计算方法采用有限体积法对控制方程进行离散，用基于同位网格的SIMPLE算法处理压强和流速的耦合关系，其中对流项采用具有三阶精度的QUICK格式，扩散项采用中心差分格式。离散后的代数方程组形式如下：

采用Gauss-Seidel迭代求解线性方程组，根据单元残余质量流量和全场残余质量流量判断是否收敛，当单元残余质量流量为进口流量的0.01%，全场残余流量为进口流量的0.5%，认为迭代收敛。

图2 纵向时均流速验证计算成

图3 机械能损失验证计算成果

3.2 验证计算分别利用文献［1］及文献［11］的实验资料就时均流速、雷诺应力与紊动强度、机械能损失进行了验证计算，限于篇幅，仅给出了部分验证计算成果。图2给出了纵向时均流速计算成果与尼古拉兹实验成果的比较，其实验工况为：管径d=0.05m，相对光滑度；图3给出了机械能损失系数的计算成果与尼古拉兹实验成果的比较。由图可知，计算成果与实验成果均吻合较好。

3.3 模拟计算分别对管壁相对光滑度为76和150的两组圆管流进行模拟计算，相关成果如下：

3.3.1 机械能损失的变化 机械能损失系数λ的计算成果见图4—图5。图中纵坐标为图中还给出了计算成果与尼古拉兹实验及柯尔布鲁克实验成果的比较。由图可知：（1）在水力光滑区，η仅与粗糙雷诺数有关，与相对光滑度无关；（2）在水力粗糙区，η与粗糙雷诺数及相对光滑度均无关；（3）在水力过渡区，η与粗糙雷诺数及相对光滑度皆有关。

3.3.2 机械能损失的构成 采用式（5）计算相应于时均流速梯度及紊动能耗散的机械能损失系数与，其成果见图4与图5。由图可知：（1）在机械能损失中，总体上来看λ1占λ的比例很小，不超过5%，其值还随雷诺数的增加而减小，随相对光滑度的增加而略有减小；（2）在机械能损失中，起主要作用，其还随雷诺数的增加而增加并趋于不变。

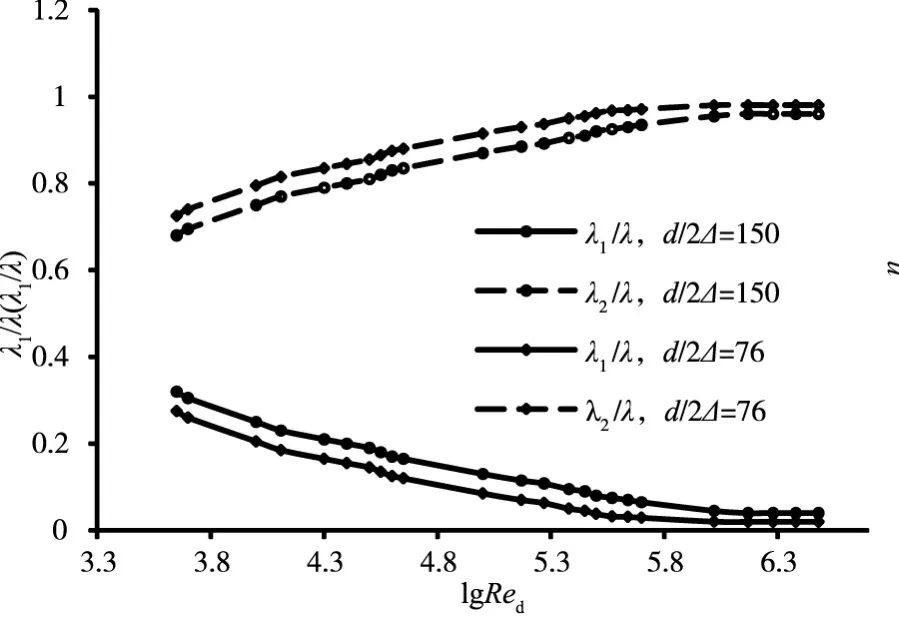
图4 机械能损失系数的构成随雷诺数Red的变化

图5 机械能损失系数的变化

4 结论

通过理论分析与数值模拟，得到如下成果：（1）对管壁均匀密集加糙的恒定圆管流建立了一个新的总流机械能方程。该方程考虑了紊动的作用，且机械能损失项有表达式。（2）管壁均匀密集加糙恒定圆管流的总流机械能损失由水体的黏性作用所导致，其随雷诺数与管壁光滑度而变，且可进一步分解为与时均流速梯度相关的损失及与紊动耗散相关的损失两部分；前者随雷诺数的增加而减少，后者则随雷诺数的增加而逐渐增加并趋于不变。

参 考 文 献：

［ 1］ 武汉水利电力学院.水力学［M］.北京：水利电力出版社，1960：201-252.

［ 2］ Colebrook C F，White CM.Experiments with fluid friction in roughened pipes［J］.Proceedings of the Royal Soci⁃ety of London，Series A，Mathematical and Physical Sciences，1937，161（906）：367-381.

［ 3］ Brown G O.The history of the Darcy-Weisbach equation for pipe flow resistance［C］//Fredrich，A.，Rogers，J.（Eds.），Proceedings of the 150th Anniversary Conference of American Society of Civil Engineers.Washington D. C.：American Society of Civil Engineers，November 3-6 2002：34-43.

［ 4］ McKEON B J，ZAGAROLA M V，SM ITSA J.A new friction factor relationship for fully developed pipe flow［J］. Journal of Fluid Mechanics，2005，538：429-443.

［ 5］ 贺益英，赵懿珺，孙淑卿，等.弯管局部阻力系数的试验研究［J］.水利学报，2003（11）：54-58.

［ 6］ LIU Shi-he，XUE Jiao，FAN Min.On the calculation of mechanical energy loss for steady pipe flow of homoge⁃nous incompressible fluid［J］.Journal of Hydrodynamics，2013，25（6）：912-918.

［ 7］ LIU Shi-he，FAN Min，XUE Jiao.Themechanical energy equation for total flow in open channels［J］.Journal of Hydrodynamics，2014，26（3）：416-423.

［ 8］ Liu Shi-he，Xue Jiao.Theoretical analysis and numerical simulation of wall resistance and mechanical energy loss for steady open channel flow［J］.Journalof Hydrodynamics，2010，22（1）：103-109.

［ 9］ Liu SH，Yin SR.Turbulent flows around sand dunes in alluvial rivers［J］.Journal of hydrodynamics，2010，22（1）：103-109.

［10］ 刘士和，刘江，罗秋实，等.工程湍流［M］.北京：科学出版社.2011.

［11］ Grass A J.Structural features of turbulent flow over smooth and rough boundaries［J］.Journal of Fluid Mechan⁃ics，1971，50（02）：233-255.

［12］ Shockling M A，A llen J J，Smits A J.Roughness effects in turbulent pipe flow［J］.Journal of Fluid Mechanics，2006，564：267-28 5.

［13］ TAM IM I.On Turbulent Flow Near aWall［J］.Journal of Communication and Computer，2012（9）：1104-1109.

A new mechanical energy equation for total flow in uniformly and densely roughed pipes and numerical simulation of the flow

PAN Wenhao，LIU Shihe
（Water Resourcesand Hydropower Engineering School ofWuhan University，Wuhan 430072，China）

The energy（the mechanical energy）equation is the theoretical basis for hydraulics；the calcula⁃tion of the energy（the mechanical energy）loss is one of the main research contents of hydraulics and engi⁃neering fluid mechanics as well as a concerned issue in engineering.The energy equation in hydraulics used to be deduced from the Bernoulli’s equation for the ideal incompressible fluid in gravitational field.It fails to reflect the effect of turbulence on the flow directly，or give a specific formula of the energy loss. This paper is written on the basis of our existing research.By theoretical analysis and numerical simula⁃tion，the results are obtained as follows∶（1）a new mechanical energy equation for total flow in uniform ly and densely roughed pipes are built；（2）research on the energy loss and the constitution of the flow in uniform ly and densely roughed pipes is made through numerical simulation.The effect of turbulence is tak⁃en into account in this equation.The results of the research show that the mechanical energy loss for total flow in uniform ly and densely roughed pipes varies with the Reynolds number and the roughness of the wall，and it can be divided into the loss related to the time averaged velocity gradients and the loss relat⁃ed to turbulence dissipation.

pipe flow；uniformly and densely roughed；mechanical energy loss；turbulence

TV131.2+9

：Adoi：10.13244/j.cnki.jiwhr.2015.05.010

1672-3031（2015）05-0375-05

（责任编辑：李福田）

2015-08-09

潘文浩（1991-），湖北武汉人，博士生，主要从事水力学及河流动力学研究。E-mail：panwenhao4732@sina.com

刘士和（1962-），湖北公安人，博士，教授，主要从事流体力学与水力学及河流动力学研究。E-mail：shihe3086@163.com