不确定性原理在光波衍射中的表象

陈海燕

(长江大学物理与光电工程学院，湖北荆州 434023)

0 引言

众所周知，光波具有波—粒二象性［1，2］。人们能从波动与粒子两方面描述光的本性，光波模式和光子态是等价的。从波动观点看来，光波是横电磁波，可用干涉和衍射现象来证明其波动性;另一方面，从粒子观点看来，光波是由光子组成的粒子流，光子的运动行为与其它微观粒子一样遵守量子力学不确定性原理［3，4］。理论上讲，光波传输的衍射规律与微观粒子所遵从的量子力学不确定性关系具有一致性。然而，现有《激光原理》及《激光原理与技术》两本教材都没用表达式描述两者之间的一致性。笔者在此给出了光波衍射规律与不确定性原理之间对应的关系式。

1 基模高斯光束的衍射规律

现以一维基模高斯光束在空间传输情形为例，导出光波空间衍射规律，如图1所示。

光束的光腰半径为ω0，，在光束传播方向上距离光腰z处的光斑半径为［5］

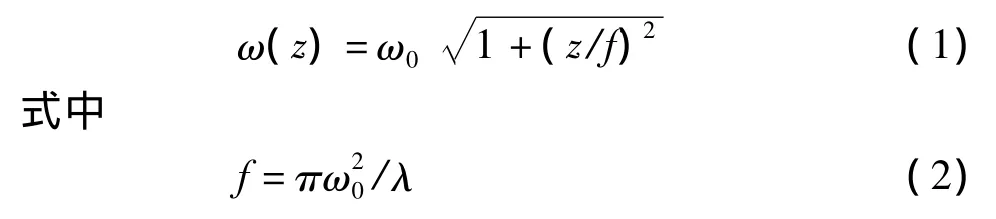
这里λ为光波波长。距离光腰无限远处，光束的发散角(即衍射角)为

令光腰直径D=2ω0。从式(3)可得到基模高斯光束的远场发散角与光腰直径的乘积为

这里，β是一个常数，其大小依赖于光场振幅分布，式(4)又称为衍射极限。

2 基模高斯光束传输的不确定性描述

另一方面，我们可将基模高斯光束的传输看作是光子通过直径为D(光腰直径)的圆孔的运动过程，当光子作为粒子处理时，其运动行为遵从量子力学不确定性原理，令光子在位置x处的动量为P，根据量子力学不确定性原理，光子的动量和位置不能同时确定，在二维相空间下满足不确定关系

式中h为约化普兰克常数，Δx和Δpx分别为光子位置和动量的不确定量。根据德布罗意公式

比较式(4)和式(7)，可得β=1/(2π)。

3 结语

公式(4)和(7)表明:基模高斯光束在空间的传输过程遵守量子力学不确定原理，其远场发散角与光腰直径的乘积即为量子力学不确定原理在衍射中的具体表象。本文所得结论适用于任何光束(如高价高斯光束)的传播问题。

［1］L.Mandel，E.Wolf，Optical coherence and quantum optics［M］，New York.，Cambridge University Press，1995

［2］Orazio Svelto，Principles of lasers(4th)［M］，New York，Springer Science+Business Media，Inc，1998.

［3］M.A.Grado-Caffaro，M.Grado-Caffaro，The quantum potential for photons［J］，Optik，2013，124(17):3013-3014.

［4］M.A.Grado-Caffaro，M.Grado-Caffaro，A qualitative estimation of the photon rest-mass and related topics［J］，Optik，2003，114(5):239-240.

［5］陈海燕、罗江华、黄春雄编著，激光原理与技术［M］，武汉:武汉大学出版社，2011.