电动汽车电池荷电状态估算

王华杰，郑来芳

太原工业学院电子工程系，山西 太原 030008

0 引 言

为了充分利用电池里的能量，同时防止不必要的浪费，电池荷电状态是电池的一个重要参数，反映了电池能量.

一个准确的SOC指示是非常重要的，方便用户使用.设计一个精确的SOC指示系统的关键问题是电池和用户行为的不可预见性.电池充放电过程是一个复杂的动态非线性系统，创建一个可以确切描述电池充放电系统的数学模型很困难.所以准确估算电池 SOC 有相当大的难度［1－3］.

近年来，支持向量机［4－7］（ SVM）技术被广泛用在各种领域.在建立较好网络模型的前提下，神经网络法依靠大量的样本数据进行训练可以得到较好的预测精度，但神经网络可能有局部极小的问题，而支持向量机的学习算法具有全局最优解.

在本文中，模糊神经网络和最小二乘支持向量机用于估计电池的SOC，将两种方法相结合，研究他们是否能更有效地估计电池的SOC.仿真是基于电动汽车仿真软件ADVISOR，结果表明，新方法能给出更精确的估计并减少计算.

1 模糊神经网络原理

神经网络是近似和简化人类大脑的结构与工作模式.这种结构和工作模式可产生一定的功能特征，类似于人脑的行为.本文以自适应神经模糊推理系统为建模基础.

假设模糊逻辑系统中有两个输入x和y，一个输出z，那么在一阶Sugeno模糊模型具有两条“ifthen”模糊规则：

Rule 1：if x是 A1and y是 B1then

z1＝p1x＋q1y＋r1

Rule 2：if x 是 A2and y 是 B2then z2＝ p2x＋q2y＋r2

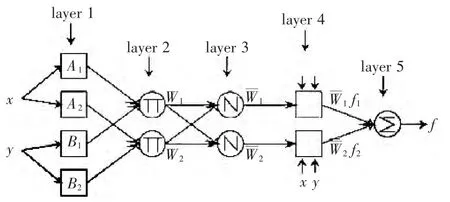
图1 ANFIS的结构Fig．1 The structure of ANFIS

在第一层中，每一个节点函数的自适应节点的功能如下：O1，i＝μAi（x），i＝1，2.

采用钟型函数作为隶属度函数：

式（1）中，｛ai，bi，ci｝是参数的集合.

在第二层中，节点的输出跟输入的关系用式（2）表示：

在第三层中，节点i是一个比率，节点的输出跟输入的关系用式（3）表示：

在第四层中，每一个节点i都是一个自适应节点.

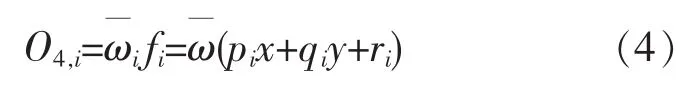
式（4）中，｛pi，qi，ri｝是参数的集合.

在第五层中，单点是被标记为一个固定节点Σ，把所有传送信号的总和作为输出.

在ANFIS中，利用神经网络法计算采样数据得到所需的参数，完成自适应建模过程.

2 基于模糊神经网络电池SOC预测模型

电池的放电性质是由多种因素的影响，可以得到如下的数据：充电电压，放电电流，电池的内部温度.SOC估计就是根据蓄电池的充电电压、放电电流和电池的内部温度的数值得到电池SOC数值.使用神经网络设计估计器的目的就是为了逼近函数：

在实际应用中，采用测量那些容易测量的因素，即监测电池的SOC，结合放电电流，电池温度的变化，电池电压变化．这种分析SOC方法被称作电化学方法.电池的电压是一个参数，它是最简单的测量，但它是反映多电池信息的参数.

为了避免由不同的电池采样值的影响，首先归一化输入数据，然后定义输入、输出变量，构造了一个一阶Sugeno模糊模型，最后使用隶属函数为每个输入进行了训练.

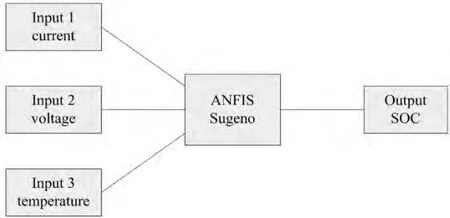
图2 一阶Sugeno模糊系统的SOC模型Fig．2 SOC model of the first－order Sugeno fuzzy system

模糊神经网络的训练过程如下：

（1）初始化模糊神经网络隶属度函数参数和系数，将所得到的数据归一化到［－1，1］，用作训练样本.

（2）设置初始权重为均匀分布的小的随机值，并设置神经元的数目，学习速率.

（3）用训练样本训练模糊神经网络和迭代法调整权重，然后计算得出输出.

3 模糊神经网络仿真

使用ADVISOR仿真软件获得所需的训练和测试数据集.ADVISOR是美国能源实验室（Natural Renewable Energy Library）开发的高级车辆仿真软件（Advanced Vehicle Simulator）.使用该软件可以搭建一个电动汽车实验平台，利用标准测试路程的模拟行驶程序，获取电动车在行驶过程中的各项参数.

动态 SOC测试是 80Ah／96V Ni－MH电池组采用混合工况UDDS－NYCC－US06_HWY混合驱动循环实验进行的.采用混合工况试验数据进行研究是让预测结果能够充分表现出电池在实际使用时的动态特性，而且也能说明此方法较好的鲁棒性和实用性.基于电动汽车仿真软件ADVISOR，将此循环运行2个周期，虚拟的电动车一共运行了4 675 s，全程29．73 m，运行过程中最大速度为80．3mph，平均速度为 22．89mph.收集的数据有速度、电流、电压、温度，如图 3、4、5、6 所示.蓄电池SOC是通过“库仑折算”的方法获得的，如图7所示.

预测误差图如图8所示.由图8可以看出，虽然最大预测误差大于0．1，但总体来说，结果大体让人满意.

图3 仿真平台下纯电动汽车车速变化曲线Fig．3 Curve of the pure electric vehicle’s speed under the simulation platform

图4 仿真平台下蓄电池输出电流变化曲线Fig．4 Curve of the battery’s output current change under the simulation platform

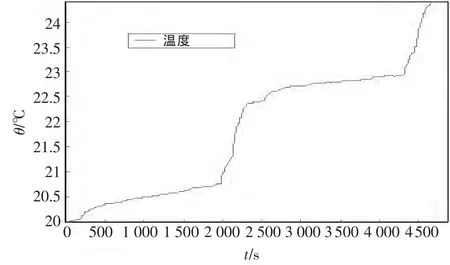
图5 仿真平台下温度变化曲线Fig．5 Curve of the variation of temperature under simulation platform

图6 仿真平台下蓄电池电压变化曲线Fig．6 Curve of the variation of battery voltage under simulation platform

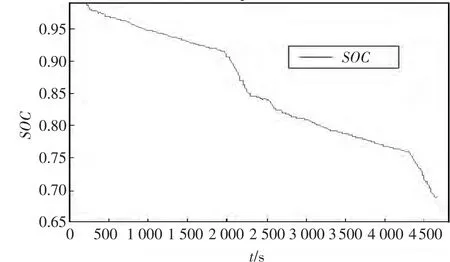
图7 仿真平台下蓄电池SOC变化曲线Fig．7 Curve of battery’s SOC change under simulation platform

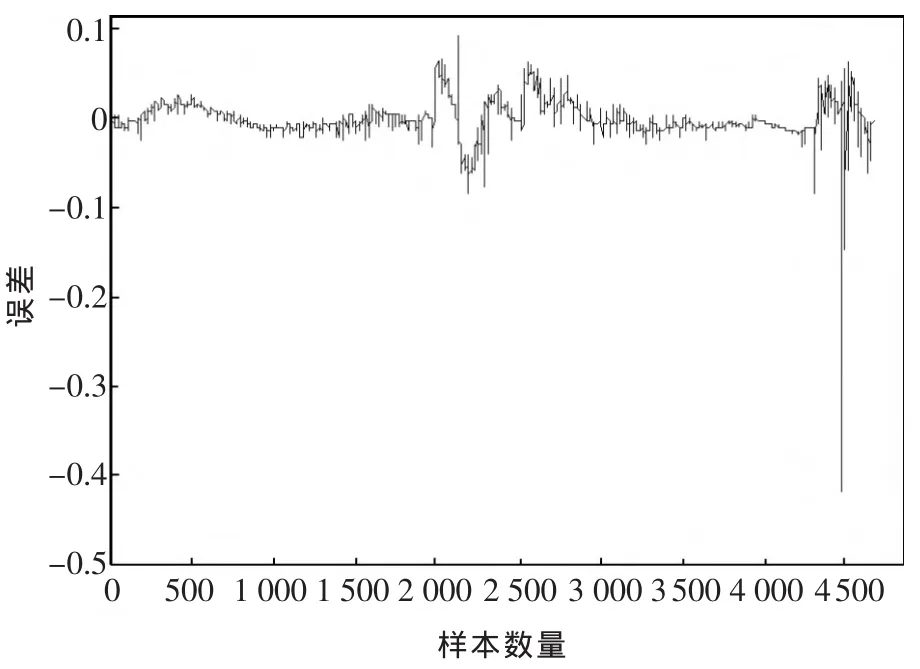
图8 基于模糊神经网络方法的预测误差图Fig．8 Error prediction based on fuzzy neural networkmethod

4 LS－SVM 原理

SVM是一种基于经验风险最小化和统计学习理论的计算学习理论，利用内核函数，可以使低维空间非线性输入映射到高维空间，能够使这些低维特征变量成为线性可分的变量.

最小二乘支持向量机可以改变复合二次规划问题转化为求解线性方程组，并且可以通过使用迭代的方式来解决，大大减少了计算量，提高了求解速度.设训练样本集T由N个样本点组成：

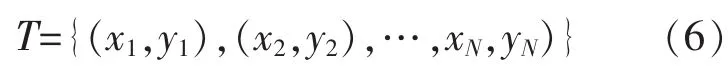
其中，xi∈Rn是输入向量，yi∈R 是对应于 xi的输出.令则优化问题是一个最小二乘支持向量机：

约束条件：

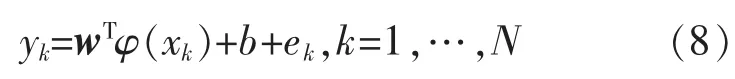
其中，w是权重向量，γ是恒定可调参数，ek是相应的误差变量，φ（·）是具有非线性映射功能的函数，使输入样本从低维空间到高维特征空间，b是一个偏差.

相应的优化问题（6）、（7）两式，可以定义一个拉格朗日函数为：

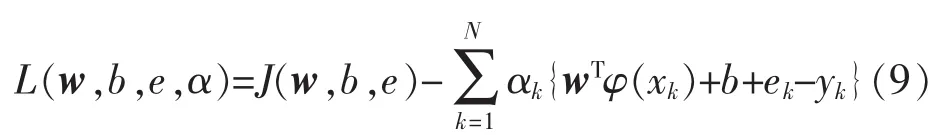
其中，αk∈R是拉格朗日乘子，用来做二次逼近.下面对等式（8）进行优化：

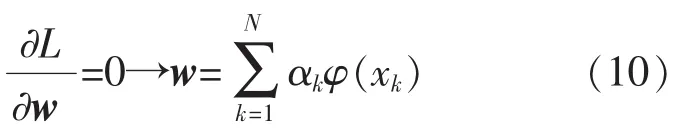
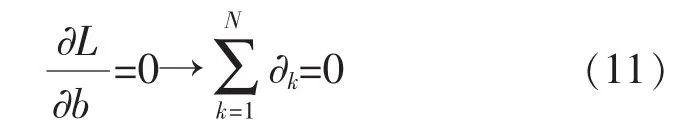
可以表示为下列矩阵的形式：

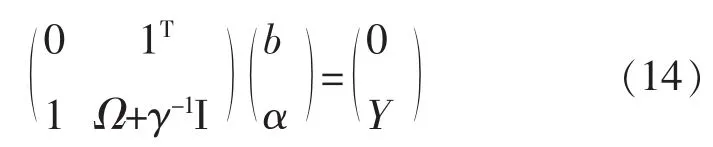
其中 Ωij＝φ（xi）Tφ（xj）＝K（xi，xj），Y＝（y1，…，yN）T，1＝（1，…，1）T，α＝（α1，…，αN）T

解方程（13）得到α和b后，对于新的输入向量x，其输出值y（x）可以根据下式进行计算：

其中，K（x，xk）是核函数.核函数从低维空间中选取特征向量，使低维空间的数据通过映射后在高维空间变得线性可分.可以看出，核函数在处理非线性问题时起到非常重要的作用.核函数之所以是最小二乘支持向量机的重要因素，是因为选择不同类型的核函数能直接决定最小二乘支持向量机的性能.目前，多项式核函数、Mercer核函数、RBF核函数等使用的比较普遍.目前，支持向量机的内核类型常选用的RBF神经.要使用支持向量机解决回归问题的数据是不是线性可分的，内核必须选择.在本文中，径向基函数被选为核函数：

5 基于LS－SVM电池SOC预测模型

在电池充放电过程中，电池荷电状态（SOC）与电池的电压、电流、温度等因素密切相关，那么用电池温度、电压、电流作为输入，电池SOC作为模型的输出.建立如下的数学方程：

最小二乘支持向量机依赖于超参数（C，ν，γ），惩罚参数C，超参数ν定义该类型的SVM回归.当RBF核被选作为核函数时，γ就表示为内核参数.对于核函数来说，内核参数是非常重要的，因此在升高学习和泛化能力方面起着决定性作用，增强预测模型性能就必须准确选择内核参数.

超参数的选择，是通过每个组合都使用八倍交叉验证，然后选用最佳的交叉验证精度的参数.根据式（10）来求出α和b的值，然后把模型参数引入到LS－SVM预测模型中，那么输入测试样本后，就可以得到预测电池SOC.将预测值与SOC的实验数据进行对比，以验证基于LS－SVM算法电池SOC预测模型的性能.

6 LS－SVM 仿真

基于LS－SVM电池SOC的预测模型预测过程的具体步骤如下：

（1）选择样本数据，进行数据处理，生成训练样本集和预测样本集；

（2）建立一个核函数 K（xi，xj）和参数 C、γ，并选择核函数的类型和惩罚系数；每个参数组合经过八倍交差验证，得到最佳的参数.本文得到的参数为：C＝0．707 107、γ＝2．828 43、均方误差 MSE＝2．866 42e－005.

（3）通过训练样本建立目标函数，并通过求解二次规划问题找到最佳的超平面，得到拉格朗日乘子α和b；

（4）建立与所获得的参数的预测模型，并预测未来的预测值与测试样本集.

预测误差如图9所示，LS－SVM预测的电池SOC的结果与试验结果相符合，它的最大预测误差小于 0．5%，并且相关系数 R＝99．99 09%，运行了599．933 132 s.

图9 基于LS－SVM方法的预测误差图Fig．9 Error prediction based on LS－SVM method

7 基于模糊神经网络和LS－SVM电池SOC预测

这里提出将模糊神经网络和LS－SVM相结合的SOC估算方法，预测步骤大致如下：首先，LSSVM来估计SOC和规范初始误差；然后它被模糊神经网络取代时预测SOC接近实际值.经过一段时间，LS－SVM用来取代模糊神经网络，校正累积的偏移量，然后再次切换到模糊神经网络，依此类推.将两者合并交替使用方法的预测误差如图10所示.可以看到，预测数据与实验数据的变化是相同的.均方误差 MSE＝2．798 04e－005，相关系数R＝99．991 2%，运行了 488．245 310 s.

不过发现当SOC较大和较小的时段，预测误差相对大一些.引起这种情况大致有以下几个原因：（1）在SOC较大和较小的时段，有大电流的充放电，引起较大误差的产生；（2）汽车运行过程中不停的充放电，温度会不断的升高，电池模型也会发生相应改变，那么所建立的函数关系也不能完全适用了.鉴于这种情况，要想得到满意的试验结果，就要设法保证电池的内部温度相对稳定.这样电池模型就不用考虑电池内部温度的变化，只需要考虑外界环境温度就可以了.

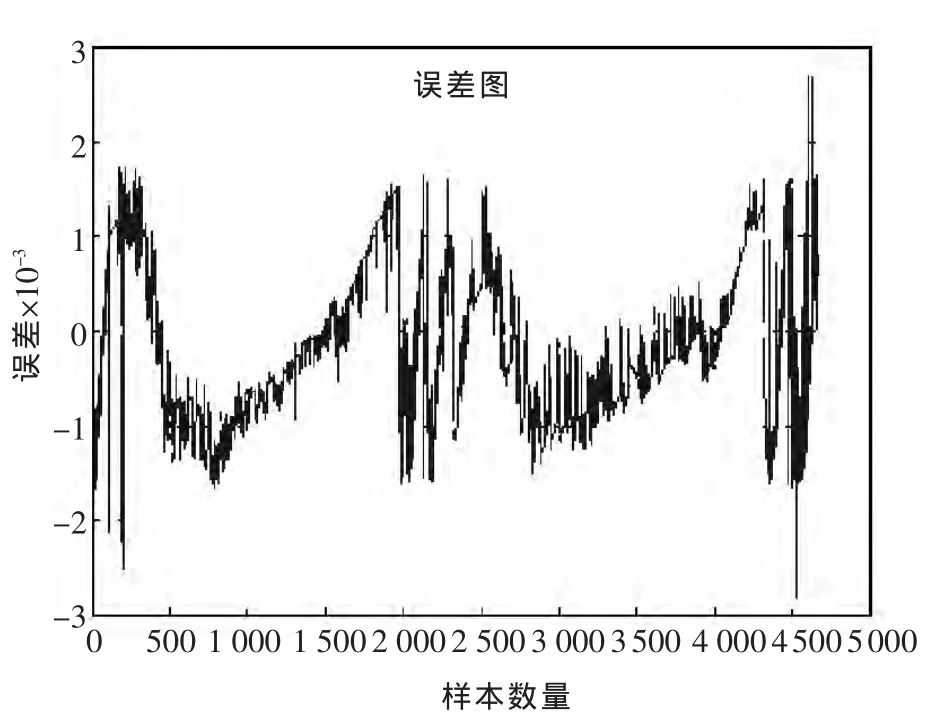
图10 基于新方法的预测误差图Fig．10 Error prediction based on the new method

实验结果表明，该LS－SVM预测的电池SOC的结果与试验结果相符合，它的最大预测误差小于0．5%，而模糊神经网络的最大预测误差大于0．1，但总体来说，结果大体让人满意，基于新方法的最大预测误差小于0．3%.由此也可以看出，基于合并的方法具有更高的精度，更好的实用性.

8 结 语

对于在电动汽车动力电池的最优控制问题，准确地估计电池的充电状态（SOC）的状态是不可忽略的部分.本文分别建立了基于模糊神经网络算法和LS－SVM算法的电池SOC预测模型，并将其交替应用到了NI－MH电池组SOC动态预测.仿真是基于电动汽车仿真软件ADVISOR，验证结果表明，此估计方法是可行的，并具有较高的精度.此预测方法不需要知道电池内部复杂的物理化学变化，反映了它良好的适应性，不仅可以准确的估算SOC，而且能减少计算量，所以它可以成为一个实用的电池SOC估计方法.

［1］W ANG Geng bo．The development of batteries in electric vehicles ［J］．Hu bei Automotive Industries Institute，1996，32（12）：83-86．

［2］M A you-liang，C HEN quan-shi，Q I zhan-ning.A research on the SOC Definition and measurementmethod of batteries used in EVS ［J］．J Tsinghua Univ（Sci＆Tech），2001，41（11）：95－97．

［3］邵海岳，钟志华，何莉萍，等．电动汽车动力电池模型及 SOC 预测方法［J］．电源技术，2004，28（10）：637－640．SHAO Haiyue，ZHONG Zhihua，HE Liping，et al．The model of Electric vehicle battery and the method of SOC’s estimation［J］．Power Technology，2004，28（10）：637－640．（in Chinese）

［4］裴晟，陈全世，林成涛．基于支持向量回归电池SOC估计方法研究［J］．电源技术，2007，31（3）：243－252．PEISheng， CHENG Shiquan，LIN Chengtao.Study on estimating method for battery state of charge based on supportvector regression［J］．Power Technology，2007，31（3）：243－252．（in Chinese）

［5］郭桂芳，曹秉刚．电动车用Ni／MH电池组剩余容量的非线性自回归滑动平均预测 ［J］．控制理论与应用，2011，28（4）：591－595．（in Chinese）GUO Gui－fang， CAO Binggang．NARMAX method for estimating the residual capacity of Ni／MH battery pack for electric vehicle［J］．Control Theory ＆ Applications ，2011，28（4）：591－595．（in Chinese）

［6］SUYKENS JA K．De Brabanter JaLukas Let alWeighted least squares support vector machines robustness and sparse approximation ［J］．Neurocomputing，2002，48（1－4）：85－105．

［7］阎威武，绍惠鹤．支持向量机和最小二乘支持向量机的比较及应用［J］．控制与决策，2003，18（3）：18－20．YAN Wei-wu，SHAO Hui-he．Application of support vector machines and least squares support vector machines to heart disease diagnoses［J］．Control and Decision，2003，18（3）：18－20．（in Chinese）