残缺判断矩阵排序的不补全策略

戴建华,于春龙

（南京理工大学 经济管理学院，南京 210094）

0 引言

在群决策过程中，由于问题的复杂性、决策时间的紧迫性和所具备专业技能的局限性，一些专家可能很难给出某方案的某个属性判断值——评价信息出现残缺。对于残缺判断矩阵排序问题的研究，目前国内外提出的解决方案较多的是基于填补的思想。例如，较早的残缺判断矩阵研究者Laarhoven与Pedrycz[1]，他们给出了残缺三角模糊判断矩阵的最小二乘排序方法。国内以徐泽水、樊治平、姜艳萍[2～4]等为代表，基本也是通过各种方法估算矩阵中的残缺元素，对残缺矩阵进行补全，进而在完整的判断矩阵上对方案进行排序。而不填补残缺信息，利用现有的评价信息直接对多属性方案进行排序的研究还比较少，本文尝试在信息补全的思路之外，结合前景理论，在不补全信息而直接排序方面进行一些探索。

1 相关概念

1.1 前景理论的涵义

Kahneman和Tversky于1997年提出前景理论[5]，后来发展成为累积前景理论。前景理论的前景价值是由价值函数和决策权重函数共同确定的，即：

1.2 残缺矩阵的描述

其中：α和β分别表示受益和损失区域价值幂函数的凹凸程度[6]，α，β＜1表示敏感性递减；θ表示损失区域比受益区域更陡的特征，θ＞1表示损失厌恶。

（2）决策函数。

Tversky等给出的决策权重的公式为[7]：W(Ai)=π(p(Ai))。其中：w为权重函数，p为判断概率，Ai为考虑的事件，π为风险下的概率权重函数。判断概率p(Ai)由决策专家给出，但在某些风险不确定的决策中，判断概率会出现违法概率二元互补关系的情况。因此，在风险决策权重的分析中，有必要考虑由于决策者对不确定源的偏好及对未知概率事件的判断所带来的影响[8]。可有如下函数获得权重函数[9]：

2 基于前景理论的残缺矩阵排序方法

2.1 原始判断矩阵的规范化处理

对于多准则决策问题，常见的准则类型是效益型和成本型。为消除不同物理量纲对决策的影响[10]，决策时需要对残缺决策矩阵Ak中的元素进行规范化处理。本文采用[-1,1]线性变换方法对Ak进行规范化处理，令：

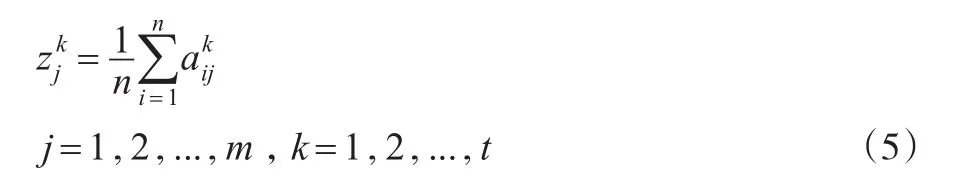
其中有残缺元素的矩阵，上述公式需要做一定的修正。假设对应上述的残缺判断矩阵Ak，如上式（4），在准则uj下，有l个残缺评价值，则在计算时需将残缺元素当成0，即上述式（5）需修正为：

2.2 正负理想方案的确定

根据前景理论，决策者在进行决策时，往往会根据某些参考点来衡量决策的收益和损失。本文运用TOPSIS方法的思想，令：

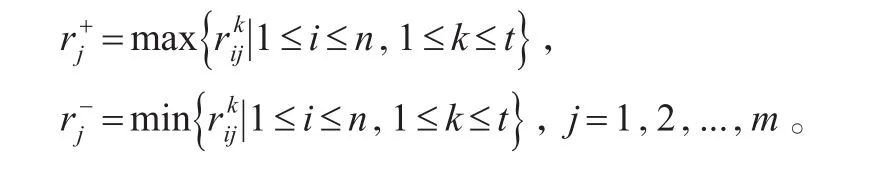
则正负理想方案为：

2.3 前景价值矩阵的建立

由灰色关联分析方法可知，在专家ek的评价下，方案xi与正负理想方案x+和x-关于准则uj的关联系数分别为：

2.4 最优综合前景值模型的修正

根据前景理论相关知识可知，在单个专家ek的评价下，如果评价矩阵中没有出现残缺元素时，方案xi的综合前景值为正前景值与负前景值之和，即：

2.5 群体意见下最优综合前景值的计算及方案排序

3 算例分析

假设有4个方案x1，x2，x3，x4，每个方案有4个准则（均为效益型准则），准则的权重为W：

4 结论

针对多属性群决策残缺矩阵的排序问题，本文提出一种基于前景理论的解决方法，在已有评价信息的基础上，对方案综合前景值最大化的优化模型进行相应修正，最终以最优综合前景值对方案进行排序。在一定程度上减少了信息填补方法带来的主观性，是对群决策排序理论中残缺信息处理方法的补充。当然，尽管本文对评价矩阵由于残缺元素的缺失带来的误差进行了控制，但是该方法的决策精度会不会因为缺失元素数目的增多而受影响？残缺元素的个数应该控制在怎样的范围？本文将对此做相应的后续研究。

[1]Van Laarhoven P J M,Pedrycz W.A Fuzzy Extension of Saaty's Priority Theory[J].Fuzzy Sets and Systems,1983,11(1).

[2]徐泽水.残缺互补判断矩阵[J].系统工程理论与实践,2004,24(6).

[3]Xu Z S.Goal Programming Models for Obtaining the Priority Vector of Incomplete Fuzzy Preference Relation[J].International Journal of A-pproximate Reasoning,2004,36.

[4]姜艳萍,樊治平.基于模糊判断矩阵的一种方案排序方法[J].东北大学学报,2000,21(4).

[5]Kahneman D,Tversky A.Prospect theory：An Analysis of Decision Under Risk[J].Economica,1979,47(2).

[6]余德建,吴应宇等.基于前景理论的信息不完全的区间型多属性决策方法[J].软科学,2011,(3).

[7]Tversky A,Fox C R.Weighting Risk and Uncertainty[J].Psychological Review,1995,102(2).

[8]万树平.区间型多属性决策的心态指标法[J].控制与决策,2009，(1).

[9]Wu G,Gonzalez R.Curvature of the Probability Weighting Function[J].Management Science,1996,42(12).

[10]徐泽水,达庆利.区间排序的可能度法及其应用[J].系统工程学报,2003,18(1).

[11]Tversky A,Kahneman D.Advances in Prospect theory：Cumulative Representation of uncertai-nty[J].J of Risk and Uncertainty,1992,5(4).

[12]李武,岳超源等.最小化序数偏好距离的多属性群决策[J].系统工程与电子技术,2010,32(2).