基于改进灰色马氏链模型的齿轮寿命分析**
2015-04-25马峻王京
马 峻 王 京
(北京电子科技职业学院汽车工程学院,北京100026)
机床的工作精度和使用寿命在很大程度上取决于其齿轮系统的寿命。传统的寿命可靠性试验是通过将样品放在模拟或真实的工作环境下测量其在一定工作循环次数后的失效状态,并利用次序统计量理论来进行可靠性特征的最后确定,统计失效率、平均可靠性指标。这样的实验需要大量的样本、时间以及繁琐的分析过程,并且实验所得数据还存在大量不完全明确的信息。
1 组合模型方法
为了得到更准确的寿命信息,可以采用数学模型的方法进行分析预测[1]。随着人们对数学模型研究的深入,可以用来进行说明预测的数学模型种类很多,如灰色模型、马尔科夫模型、指数回归模型等。但单一的数学模型往往具有一定的缺陷,无法进行高精度分析。例如灰色模型对于离散变量的预测精度无法较好控制,且一般只用于小样本数据,当数据较多,离散程度较大时,其灰度较大,预测精度较差[2];马尔科夫过程则偏重无后效性数据序列的预测[3-4];指数回归模型则要求大量的样本且具有较好的分布规律[5]。近年来通过将不同模型预测方法进行优化组合产生新的组合模型进行预测的方法发展迅速[6-9],这为齿轮寿命的分析预测提供了新的思路。
2 遗传粒子群-灰色马氏链组合模型
2.1 灰色GM(1,1)模型预测
选取某品牌汽车自动变速箱某一档位齿轮为寿命试验对象,抽取100 个样本进行失效个数为10 的无替换定数截尾实验,齿轮寿命如表1 所示。

表1 实验数据
以1 ~5 号数据为基础,建立原始数列x(0)。
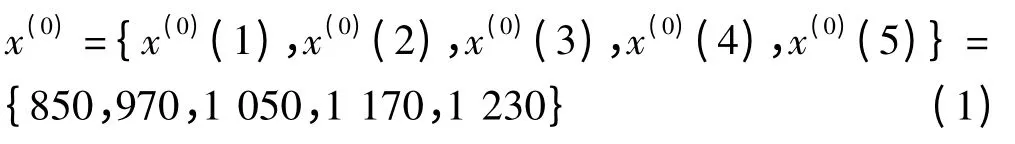
对x(0)进行一次累加(1 -AGO)生成x(1)。

x(1)的紧邻均值生成序列:

式中:z(1)(k)=4,5。

对生成的序列x(1)建立GM(1,1)模型微分方程,即

根据z(1)和x(0)可列出
利用最小二乘估计参数列满足方程â=(BTB)-1BTY,求解出a和b

则微分方程为

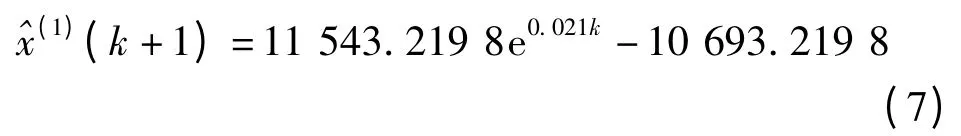
将其还原成GM(1,1)模型的预测值:

由式(8)求得的预测数据与实际数据的对比如表2 所示,根据GM(1,1)模型得出的预测值求出预测值与实际值之间的残差ε(0)(k)=x(0)(k)-^x(0)(k),进而求得残差相对值
2.2 灰色马氏链模型预测
马氏链即马尔科夫过程,于1906 年由前苏联数学家A.A.Markov 提出,经过一百多年的演变,在理论上已十分完善,是随机过程领域的重要组成,对于无后效性数据序列的预测精度较高。
在灰色模型的基础上,将残差相对值划分为若干个状态,每个状态区间为σi=[Li,Ui),结合表2 的数据,具体划分为σ1=[-10%,-5%);σ2=[-5%,0);,σε=[0,5%),σ4=[5%,10%)4 个状态。残差相对值所对应的状态划分结果如表2 所示,建立马氏链模型。

表2 灰色GM(1,1)模型预测结果及残差
转移1 步所对应的概率矩阵

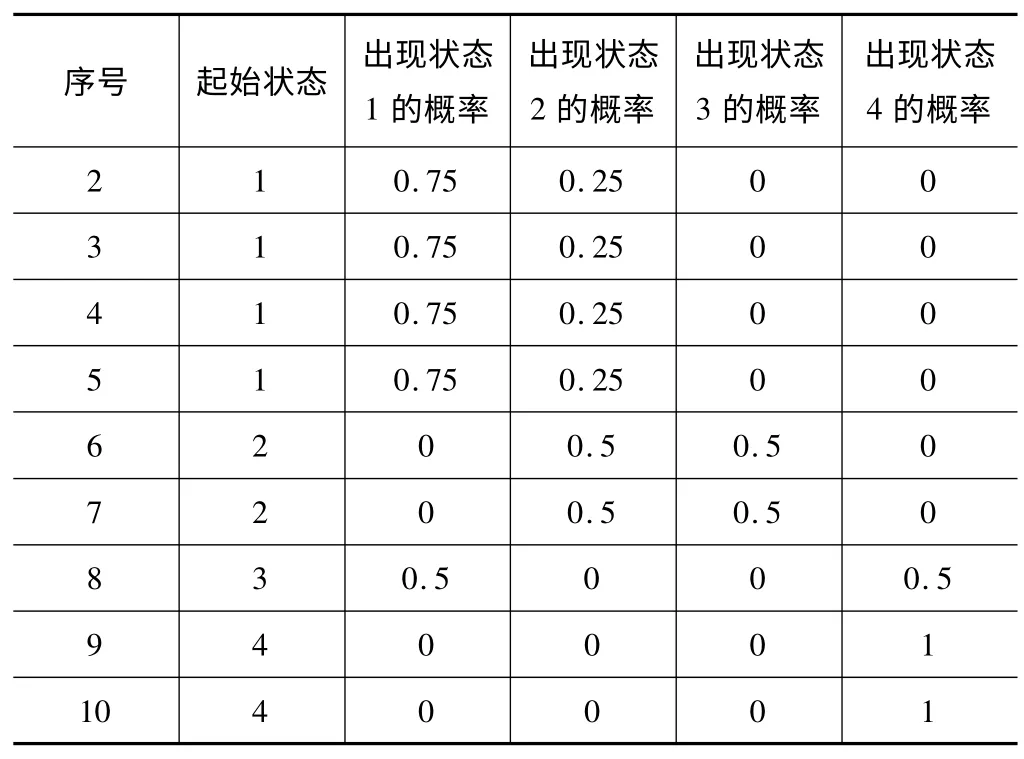
表3 转移1 步后出现各状态的概率

表4 灰色模型预测与灰色马氏链模型预测值比较
对比两种模型的预测值可以看出灰色马氏链模型比单一的灰色模型预测精度更高,误差更小。可见灰色马氏链模型更适合处理此类随机波动性较大的问题。但任何预测模型都不能完全做到绝对准确,因此,灰色马氏链模型仍有改进的空间。
2.3 遗传粒子群修正的灰色马氏链模型预测
由上述计算可以发现对于残差序列的状态,中间值并不一定是最好的选取结果,最好的结果可能是状态区间中的某一个值。若把状态所在的区间σi=[Li,Ui)设定为结果不确定的灰区间,对这种灰区间的白化方法应该表示为=(1 -ε)Li+εUi。式中:ε 称为白化系数,应满足ε∈[0.1]。灰色马氏链模型的预测结果实际上是取ε=1/2。
对此类问题的优化设计算法常见的有梯度法[10-11]、牛顿类法[12-13]、变尺度法[14]、惩罚函数法[15]、遗传算法[16-17]等。在非线性问题优化方法中,遗传算法(GA)是对问题变量的编码集进行操作,从一个点群开始寻优,因此可以获得全局最优解,具有广泛的实用性。粒子群算法(PSO)则是模拟鸟群在觅食过程中发现的。其通过个体间的相互竞争与协作来解决复杂空间中的最优解的搜索问题[18],而遗传算法与粒子群算法的混合模式(GA -PSO)比其他类型算法的混合模式具有更好的优化效果[19]。混合算法中以遗传算法为基础,进行原始种群的产生、选择、交叉、变异等计算,同时为提高连续变量的优化水平,选取部分基因,固定其中的离散变量值,再采用离子群法对连续变量值进行优化计算,然后将结果替换原始种群,返回遗传算法,循环上述规则,直至满足终止条件。其总体流程如图1 所示。
算法实现:
步骤一:随机产生多组编码与固定的离散变量组成粒子群,每个粒子代表一个白化系数。
步骤三:更新粒子适应度,用每个粒子当前的适应度值与自身当前最好的适应度值作比较,若当前适应度值较小,则取代最好适应度,作为新的当前最好适应度,进而得到当前白化系数的最优解。
步骤四:更新粒子群适应度,用每个粒子当前最好适应度与粒子群的最好适应度作比较,得到当前最优白化系数值。
步骤六:判断是否满足终止条件,如果满足,则终止循环,如果不满足,则回到步骤二,直至找到最优解,输出优化粒子群。
上面提到的4 个灰色区间为σ1=[-10%,-5%];σ2=[- 5%,0];σε=[0.5%〕,σ4=[5%,10%),它们的白化表示为:
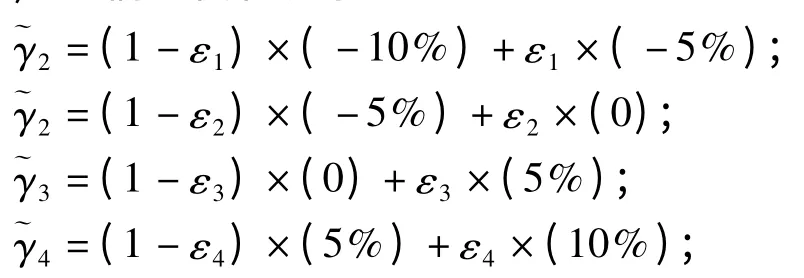
式中:εi∈[0,1],i=1,2,3,4。
计算中,选取粒子长度为4,粒子数为500,学习因子c1=2;c2=2,加权因子ω=1,迭代次数为800,粒子更新位置最大为1,最小为0,粒子更新速度最大为0.01,最小为-0.01.通过MATLAB 计算,取ε =[ε1,ε2,ε3,ε4]=[0.4,0.4,0.5,0.7]
经过计算后,其预测值如表5 所示。
3 结语
(1)使用单一的灰色GM(1,1)模型分析变速箱齿轮问题精度较差,标准差为7.2%。

表5 各种模型预测值、残差值及标准差比较
(2)灰色马氏链模型能够有效提高分析预测的精度,使标准差下降到3.4%,这种组合模型更适合描述随机性较大的问题。
(3)利用遗传粒子群算法(GA-PSO)对灰色马氏链模型的参数进行修正后,精度进一步提高,标准差仅为1.9%。计算表明该种修正后的组合模型对于变速箱齿轮寿命类随机性较大的离散问题具有很好的分析水平和预测精度。
[1]谢常青,赵延明.车用电子设备电子器件寿命组合预测[J].测试技术学报,2008(3):189 -193.
[2]刘思峰,郭天榜,党耀国.灰色理论及应用[M]. 北京:科学出版社,1999:44 -60.
[3]Wu Kai,Lin Zhenghui. Application of Markov chain in VLSI power estimation[J]. Computer Engineering,2003,29(13):162 -164.
[4]A T 巴鲁查,赖特. 马尔科夫过程论初步及其应用[M].上海:上海科学技术出版社,1979.
[5]陈玉祥,张汉亚. 预测技术与应用[M]. 北京:机械工业出版社,1985:48 -50.
[6]谢敬东,唐国庆,徐高飞. 组合预测方法在电力负荷预测中的应用[J].中国电力,1998,31(6):3 -5.
[7]李振亮.组合预测方法在大气环境评价中的应用[J]. 数理统计与管理,1997,16(4):12 -15.
[8]王居平.组合预测方法及在图书馆管理中的应用[J]. 情报杂志,2002(8):61 -63.
[9]袁文华,鄂加强,龚金科,等. 柴油机连杆轴颈磨损量组合预测模型及应用[J].湖南大学学报:自然科学版,2006,33(3):71 -74.
[10]Prager W ,Shield R T. Optimal design of multi - purpose structures[J]. Journal of Solids and Structures,1968,79 -82.
[11]Prager W,Taylor J E. Problems of optimal structural design[J]. Journal of Applied Mechanics,1985,gs(1),115 -121.
[12]Fleury C,Sander G. Relations between optimality criteria and mathematical programming[C]. Proc. Symposium on Applications of Computer Methods in Engineering,University of Southern California,Los Angeles,California,1977,1121 -1125.
[13]Khot N S,Berke L,Venkayya V B. Comparison of optimality criteria algorithms for minimum weight design of Structures[C]. Structural Dynamics and Materials Conference,1978,179 -184.
[14]赵又红,符炜,罗显光. 二级圆柱齿轮减速器的多目标优化设计[J]. 湘潭大学:自然科学学报,2003,21(2):81 -84.
[15]韩伯顺.非线性规划中的罚函数及填充函数方法[D]. 上海:上海大学,2006.
[16]Shi L S,Li Z Y. An improved pareto genetic algorithm for multi-objective TSP[A]. In Proceedings of the 5th International Conference on Natural Computation(ICNC2009).Tianjin,China. 2009:585-588
[17]Liu Q. Study on multi -object optimization of logistics network based on genetic algorithm[A]. Proceedings of 2008 International Conference on Computational Intelligence and Security(CIS2008).Suzhou,China,2008.
[18]任子晖,王坚,高岳林.马尔科夫链的粒子群优化算法全局收敛性分析[J].控制理论与应用,2011(4):462 -466.
[19]梁艳春,吴春国,时小虎.群智能优化算法理论与应用[M].北京:科学出版社,2009.
