基于承载能力检算的某空腹式双曲拱桥工作性能评价分析

■张晓璐

（1.福建省交通科学技术研究所;2.福建省公路水运工程重点实验室，福州 350004）

1 概述

双曲拱桥是将主拱圈以“化整为零”的方法按先后顺序进行施工，再以“集零为整”的方式组合成承重的整体结构，它充分发挥了预制装配的优点，可以不要拱架施工，节省木料，加快施工进度，而所耗用的工料又不多。但因主拱圈分期形成，其呈现出组合结构的受力特征，故整体性较弱。本文的研究对象某多跨等截面悬链线空腹式钢筋混凝土双曲拱位于某市，全长210.6m，设计桥型为5 孔等跨连续双曲拱，单孔净跨径为35m，净矢高为5m，矢跨比1/7，采用悬链线结构形式，拱轴系数m=3.142。桥面布置为净4.5m（行车道）+2×0.45m（安全带）。主拱圈为四肋三波组成，高度为0.95m，拱肋和横隔板采用250 号现浇混凝土，拱波和拱板采用200 号混凝土。空腹拱为圆弧拱，跨度l0=2.8m，矢跨比f0/l0=1/3.5，靠墩腹拱为三铰拱，伸缩缝和变形缝贯穿桥横断面。桥墩为重力式墩，桥台采用U 型台，基础均为扩大基础。原设计荷载：汽车-10 级、履带-50(见图1)。洪水设计或然率为100 年一遇。为了解桥跨主体结构在荷载作用下的实际受力状态，检验结构是否满足汽车-10 级、履带-50 荷载正常行车使用要求，我们对该桥进行了荷载试验，并结合承载能力检算方法，来评价结构工作性能。

图1 某等截面悬链线空腹式双曲拱桥总体布置图及试验测试截面示意图 （单位：m）

2 荷载试验结果及分析

2.1 静载试验

2.1.1 静载试验工况及检验对象

根据该桥设计图纸和现场实测资料，应用MIDAS 计算软件进行建模计算，模型见图2。以设计标准活载产生的该试验项目的最不利效应值等效换算，确定所需的试验荷载。然后根据各跨拱轴线变化后的桥跨结构受力特点，确定试验工况，具体见表1，主要测试截面见图1。

2.1.2 测点布置

(1)应变测点布置：在Ⅳ-Ⅳ和Ⅵ-Ⅵ截面各拱肋拱背位置粘贴混凝土应变片，在其他控制截面各拱肋底面位置粘贴混凝土应变片，各控制截面应变测点布置见图3 和图4。

表1 试验测试内容

(2)挠度测点布置：在各控制截面上下游侧桥面位置布设塔尺进行测量，各控制截面挠度测点布置见图5。

(3)裂缝观测：对外观检查中发现的拱肋裂缝进行观测，同时观测各试验工况作用下相应截面的裂缝开展情况。

图2 某等截面悬链线空腹式双曲拱桥模型图

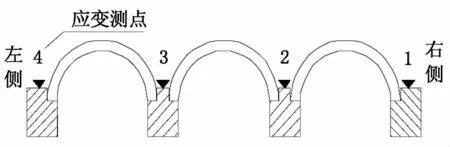
图3 Ⅳ-Ⅳ和Ⅵ-Ⅵ截面应变测点布置图

图4 其他截面应变测点布置图

图5 各控制截面挠度测点布置图

2.1.3 静载试验结果及分析

在试验加载工况作用下，各控制截面的实测挠度及其与理论计算值的比较如表2 所示，实测应变及其与理论计算值的比较如表3 所示。

经过桥梁静载试验，该桥第5 跨跨中截面挠度校验系数为0.53 和0.57，应变校验系数为0.64～0.76；第5跨L/4 和3L/4 截面挠度绝对值之和的校验系数为0.64和0.69，L/4 截面应变校验系数为0.66～0.77；第5 跨拱脚截面应变校验系数为0.67～0.78；第4 跨跨中截面挠度校验系数为0.49 和0.53，应变校验系数为0.60～0.71；第4 跨拱脚截面应变校验系数为0.65～0.71；各截面挠度和应变校验系数均小于《公路桥梁承载能力检测许定规程》 (以下简称《规程》)规定值1.00；各截面相对残余挠度最大值为14.0%，相对残余应变最大值为15.2%，均小于《规程》规定值20%。

对5-4 拱肋（第5 跨从右往左第4 片）跨中横向裂缝进行观测，在各试验工况下最大开展宽度为0.01mm，卸载后恢复；各试验工况下相应控制截面未见新裂缝产生。

表2 各控制截面挠度分析表

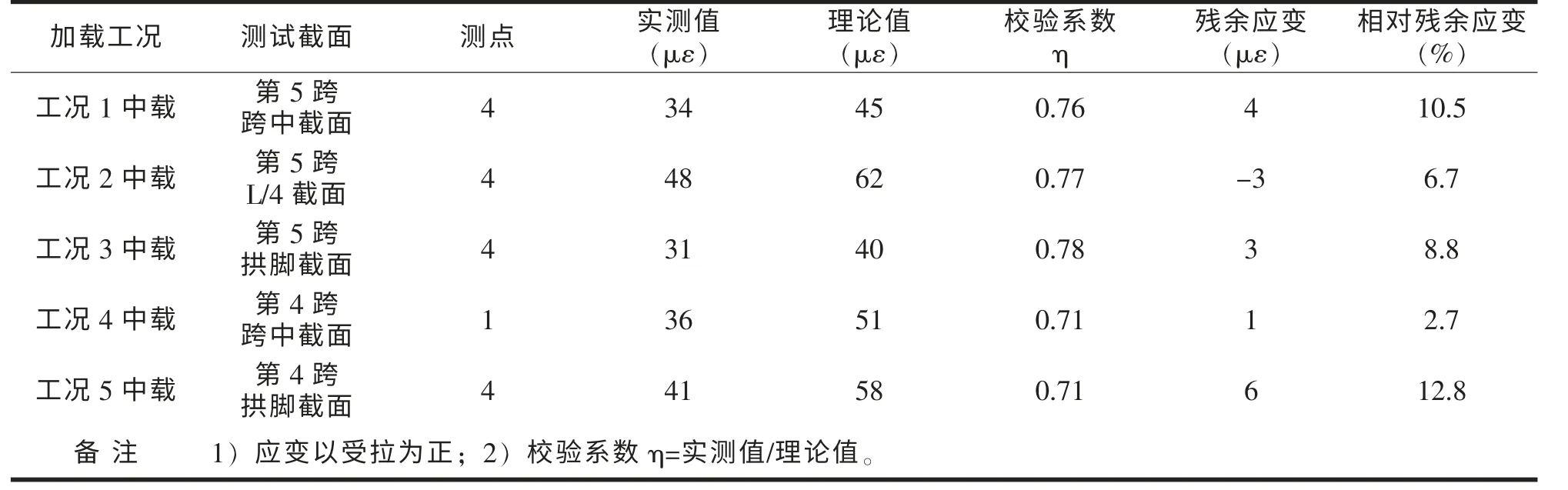
表3 各控制截面应变分析表 （每个工况仅列出最大η 值的拱肋）

2.2 动载试验

2.2.1 自振特性试验工况

在桥面无任何交通荷载以及桥址附近无规则振源的情况下，测定桥跨结构由于桥址处风荷载、地脉动等随机荷载激振而引起的桥跨结构微小振动响应，测试桥跨结构自振频率和阻尼比，以分析桥跨结构自振特性。

2.2.2 自振特性结果及分析

在各跨桥面八分点位置上放置脉动传感器，实测的信号经FFT 分析、模态分析，得到该双曲拱桥的竖向1阶和横向1 阶自振频率及振型。自振特性试验表明，该桥实测竖向1 阶和横向1 阶自振频率为4.11Hz 和1.27Hz，大于理论计算值2.63Hz 和0.87Hz，实测振型与理论计算振型基本吻合，表明结构的动刚度满足要求。竖向1 阶和横向1 阶的实测与计算自振频率及振型图对比见图6。

图6 各阶实测与计算自振频率及振型图对比

3 桥梁承载能力检算

3.1 检算资料

桥面宽度：净4.50m 行车道+2×0.45m 安全带；

拱圈计算跨径、计算矢高：35.6137m 和5.099m；

矢跨比F0/L0：1/7；拱轴系数m=3.142；

拱肋厚度：95cm；拱肋宽度：30cm；Ac=0.285m2；

车道数：1 车道，车道折减系数取1.0；

设计荷载：汽车-10 级、履带-50；

温升：+25℃；温降：-10℃。

拱肋采用250 号（即25 号）现浇砼，根据《公路钢筋混凝土及预应力混凝土桥涵设计规范》（以下简称《规范》）附录A 新旧规范的混凝土标号及两者各项设计指标的关系可知，强度等级为C23，弹性模量Ec=2.70×104MPa，泊松比=0.2，抗压强度设计值fcd=8.996MPa。

3.2 检算对象和内容

检算对象选择病害最严重的5-4 拱肋，检算内容包括桥跨结构在承载能力极限状态下相应的作用效应组合及各组合情况下的拱肋截面（包括拱顶和拱脚截面）强度验算和整体强度-稳定验算。各作用效应由MIDAS 计算软件进行建模计算，模型参见图2。

3.3 检算公式

由《规程》可知，配筋混凝土桥梁承载能力极限状态下的检算公式为：γ0S≤R(fd,ξcadc,ξsads)Z1(1-ξe)。根据《公路圬工桥涵设计规范》(以下简称《圬工规范》），上式变为：

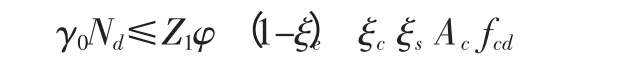
各参数详见《规程》和《圬工规范》，其中γ0=1.0，ξe=0.035，ξc=ξs=0.99；由静载试验结果可知，各拱肋挠度、应变校验系数最大值为0.78，根据《规程》规定，当进行荷载试验时，取荷载试验后的旧桥检算系数Z2代替上式Z1进行检算，根据《规程》查表得承载能力检算系数Z2=1.06。

3.4 荷载效应分析

根据《公路桥涵设计通用规范》(JTGD60-2004)，承载能力极限状态下的荷载效应采用基本组合，其表达式为：

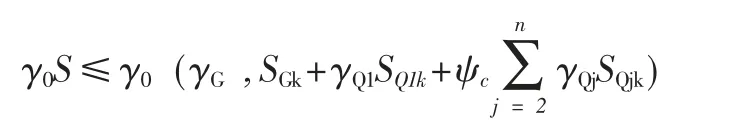
根据《公路桥涵设计通用规范》(JTJ021-89)，上式可以划分为8 个组合工况，具体见表4。各荷载效应值可从模型读取，具体值见表5。

表4 荷载效应基本组合工况表

表5 各荷载效应值表(M 单位：kN.m；N 单位：kN)

3.5 拱肋截面强度检算

根据《圬工规范》，拱肋弯曲系数φ=1.0。在承载能力极限状态基本组合作用下的拱肋截面强度检算结果如表6～7 所示。由检算结果可知，拱肋结构在荷载基本组合下，拱顶及拱脚截面的偏心距均小于容许偏心距，截面轴向力抗力值[N]均大于最不利组合轴向力Nd，表明该桥主体结构强度检算结果能满足汽车-10 级、履带-50 设计荷载等级要求。

3.6 拱肋整体“强度-稳定”检算

本桥拱肋为无铰拱，根据《圬工规范》，拱肋横向稳定计算长度l0=0.495（L0/4F0+F0/L0）L0/2=16.40m，l0/b=17.26，查表得拱肋弯曲系数φ 取0.695。在承载能力极限状态基本组合作用下的拱肋整体“强度-稳定”检算结果见表8。由检算结果可知，拱肋结构在荷载基本组合下，轴向力偏心距均小于容许偏心距，轴向力抗力值[N]均大于轴向力Nd，表明该桥主体结构整体“强度-稳定”检算结果能满足汽车-10 级、履带-50 设计荷载等级要求。

表6 5-4 拱肋拱顶截面强度检算

表7 5-4 拱肋拱脚截面强度检算

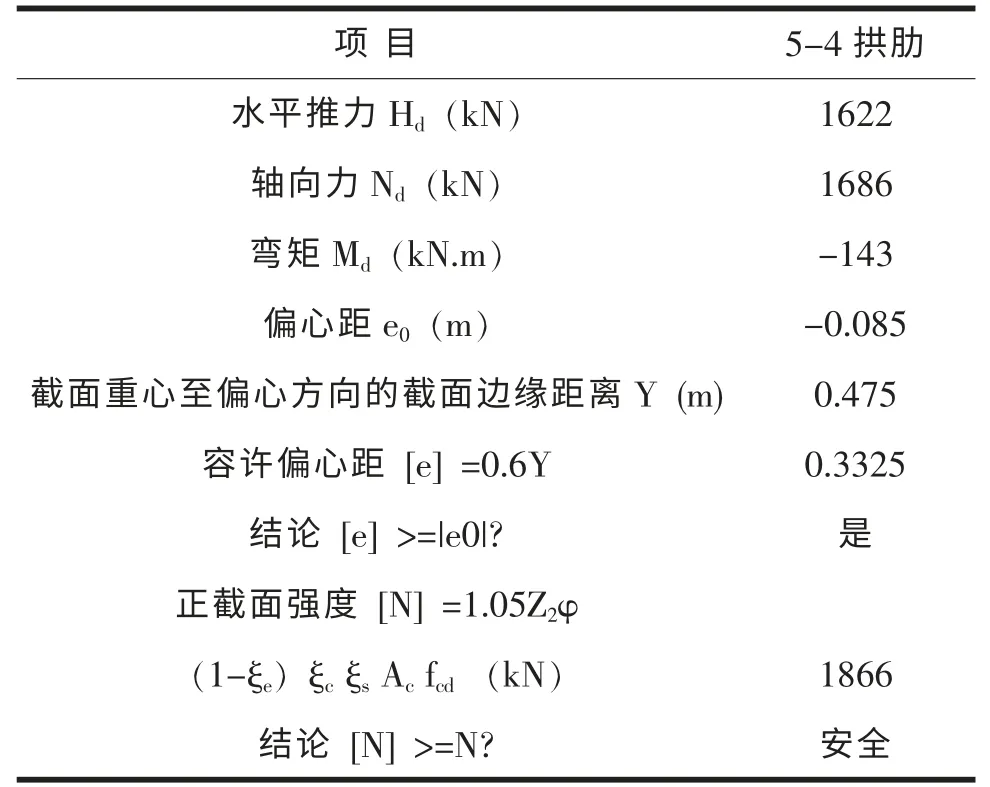
表8 5-4 拱肋整体 “强度-稳定”检算

4 结论

通过对该双曲拱桥进行静动载试验和承载能力检算，得到结论如下：

（1）桥梁静载试验表明：该桥各试验跨截面挠度校验系数为0.49～0.69，应变校验系数为0.60～0.78，各截面挠度和应变校验系数均小于《规程》规定值1.00；各截面相对残余挠度最大值为14.0%，相对残余应变最大值为15.2%，均小于《规程》规定值20%；

在各试验工况下，5-4 拱肋跨中横向裂缝最大开展宽度为0.01mm，卸载后恢复，裂缝宽度满足规范中的限定值。

（2）桥梁动载试验表明：该桥实测竖向1 阶和横向1 阶自振频率为4.11Hz 和1.27Hz，大于理论计算值2.63Hz 和0.87Hz，实测振型与理论计算振型基本吻合，表明结构的动刚度满足要求。

（3）桥梁承载能力检算表面：该桥主体结构强度和整体“强度-稳定”检算结果均能满足汽车-10 级、履带-50 荷载等级要求。

综上所述，该空腹式双曲拱桥承载能力目前能够满足汽车-10 级、履带-50 荷载正常行车使用要求。

[1]王敏强，王乐，张桓.空腹式双曲拱桥有限元分析与试验研究.武汉大学学报：工学报，2005，38(5)：88-93.

[2]JTG/T J21-2011,公路桥梁承载能力检测评定规程.

[3]JTG D62-2004,公路钢筋混凝土及预应力混凝土桥涵设计规范.

[4]JTG D61-2005,公路圬工桥涵设计规范.

[5]JTG D60-2004,公路桥涵设计通用规范[S].

[6]JTJ 021-89,公路桥涵设计通用规范[S].