具预警功能的可修复系统解的存在唯一性

李朗

(齐鲁师范学院数学学院，山东济南250013)

可靠性数学中主要的研究对象之一就是可修复系统，在现代工程系统中研究可修复系统具有重要的现实意义。由于实际需要，可修复系统正在向提前预警与故障出现自动修复相结合的方向发展，由此在可修复系统中设计预警功能具有重要的实际意义。

文中讨论具有预警功能的两不同部件可修复系统，利用泛函分析和半群中的定理证明系统非负时间依赖解的存在唯一性，为进一步研究系统解的特性及系统主算子的一系列特性提供理论基础。

1 模型介绍

由于实际的需要，许多系统都具有预警功能，此功能可对系统具有保障作用［1］。文中研究关于两不同部件并联可修复系统［2］，相比较文献［3］此系统具有预警功能，由此改变了文献［2］的边界条件P(0)∈D(A)。

假设系统的常规故障率和修复率是常数;失效系统修复率不是常数;系统在状态C不发生部件故障而且修复后与原来系统一样可以正常工作;t=0时刻，系统正常工作。记状态0:两部件都正常工作;状态1:部件A故障，B正常工作;状态2:部件B故障，A正常工作;状态3:A，B同时故障;状态4:A，B由共因引起的系统故障［3］;状态C:预警状态，由于常规原因引起故障但系统仍能正常工作。

此模型可用如下积分-微分方程组表示:

设(x，t)∈［0，∞)×［0，∞)，各个符号表示如下:pi(t)为系统处于状态 i的概率，i=0，1，2，c;pj(x，t)d x为在［x，x+d x］内处于状态 j时的概率，j=3，4;λa为部件A的故障率;λb为部件B的故障率;λc0状态0到C的常因故障率;λc1状态0到4的共因故障率;λc2状态2到状态4的共因故障率;λc3状态1到状态4的共因故障率;μa为部件A的修复率;μb为部件B的修复率;μi(x)为故障系统在状态i并且修理时间为x的系统修复率且满足:0≤μi(x)＜∞，成立。

下面简记:

取状态空间

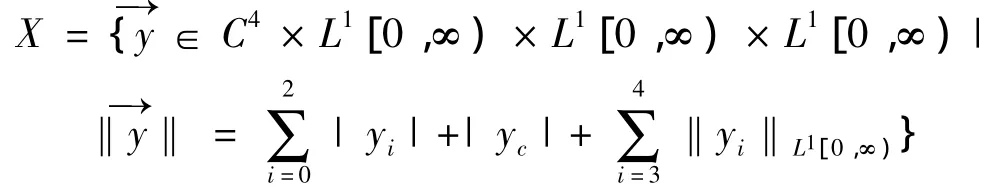
则显然(X，‖·‖)是一个Banach空间。取算子A的定义域:

pi(x)是绝对连续函数(i=3，4)且p3(0)=λbp1+λap2，p4(0)= λcpc+ λc1p0+ λc3p1+ λc2p2}，则上述系统可描述为状态空间X中的一个Cauchy问题［4］:

2 主要结论

定理1［5］设算子A，E的定义如前，则

1)当λ ＞ 0时，λ∈ρ(A)，且‖(λI－A)－1‖≤

3)T(t)是正C0半群;

4)T(t)是正压缩C0半群。

证 1)当λ ＞0时，λ∈ρ(A)且‖(λI－A)－1‖≤对任意给定的∈X，讨论方程(λI－ A这等价于:

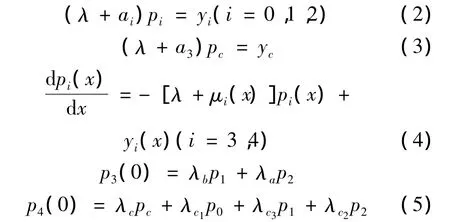
解式(2)～式(5)可得［6］

其中

再由Fubini定理可得

这说明当λ ＞0时，(λI－A)－1:X→X存在且

2)取集合 M={(p0，p1，p2，pc，p3(x)，p4(x))|pi(x)∈C∞0［0，∞)且存在一个常数Ci＞0使得pi(x)≡ 0，x∈［0，Ci］，i=3，4}，显见 M 在 X 中稠密，因此为了证明D(A)在 X中稠密，只需证明D(A)在M中稠密即可。

令0 ＜ 2s ＜ min{c3，c4}，显然x∈［0，2s］时有pi(x)=0(i=3，4)，令

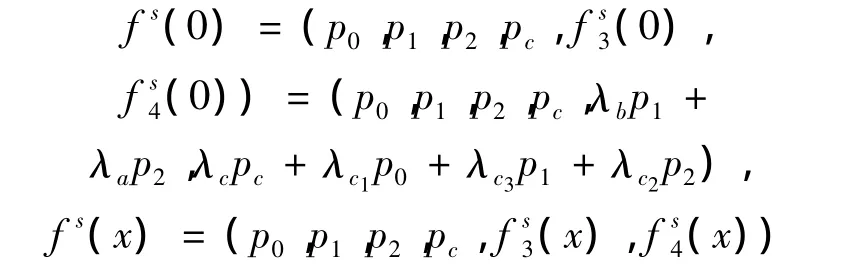
其中

这里

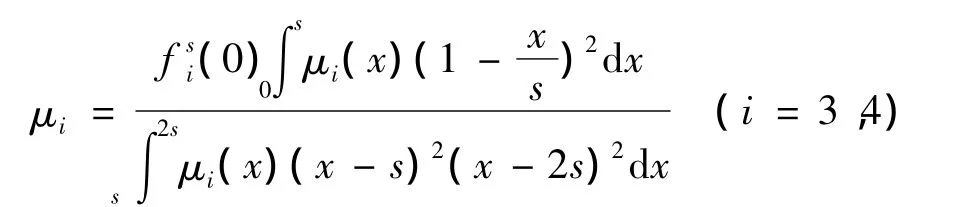
易证 fs(x)∈D(A)，且

由1)，2)和Hille-Yosida定理知:A生成一C0半群，容易验证E:X→X有界线性算子，并且由有界算子扰动定理知A+E生成一C0半群T(t)。

3)T(t)是正C0半群。由1)可知，当为非负向量时也为非负向量，这说明(λI － A)－1为正算子，同时由E的表达式可知E也是正算子;又因为

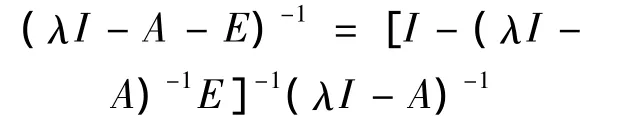
及

可知(λI－A－E)－1也为正算子，从而预解正算子A+E生成的半群T(t)是正C0半群［7］。

4)T(t)为正压缩C0半群。假设R(I－A－E)≠X，由于R(I－A－E)是闭的［8］，那么存在0≠F∈X*，使得(Q，f)=0，∀Q∈R(I－A －E);对任意∈D(A+E)有((I － A － E，f)=0;即对所有∈ D(A+E)，有，［I － (A+E)*］F)=0，即(A+E)*F=F。

也就是说，1是(A+E)*的本征值，但1显然不是本征值，故假设不成立，因此有R(I－A－E)=X。

其中

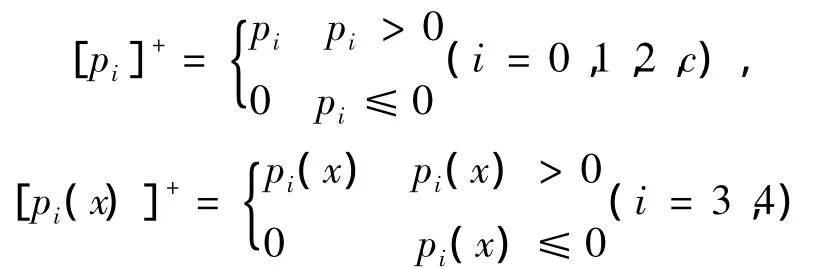
由式(7)和弥散算子的定义知，A+E为弥散算子，结合1)，2)，3)及Phillips定理知:A+E生成正压缩C0半群，再由半群唯一性知这个压缩半群即是T(t)。

定理2 系统(1)存在唯一非负时间依赖解

由定理1得

‖(1，0，0，0，0，0)‖ ≤1，t∈［0，∞)

另一方面，因为(1，0，0，0，0，0)∈ D(A+E)故有∈D(A+E)，所以有Pi(·，t)，i=3，4满足系统积分-微分方程组，且有

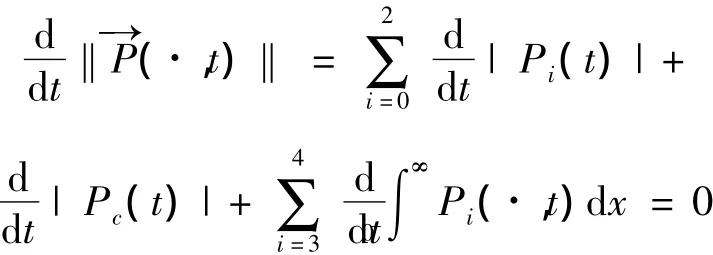
［1］高超，朱广田.具有预警功能的可修复系统［J］.应用泛函分析学报，2011，13(1):19-28.GAO Chao，ZHU Guangtian.Repairable system with warning function［J］.Acta Analysis Functionalis Applicata，2011，13(1):19-28.(in Chinese)

［2］Dhillon B S，Anuded O C.Commom-cause failure analysis of a non-identical unit parallel system with arbitraly distributed repair time［J］.Micoroelerton Relib，1993，33(1):87-103.

［3］ArendtW.Resolvent positive operators［J］.Proc London Math Soc，1987，3:54:321-349.

［4］郭卫华，许跟起，徐厚宝.两不同部件并联可修系统解的稳定性［J］.应用泛函分析学报，2003，5(3):281-288.GUOWeihua，XU Genqing，XU Houbao.The stability of solution of a parallel repairable system with two non-identical unit［J］.Acta Analysis Functionalis Applicata，2003，5(3):281-288.(in Chinese)

［5］张玉峰，金爱冬.具有多个临界和非临界错误的不完全转换的冷储备可修复系统解的存在唯一性［J］.数学的实践与认识，2004，34(12):137-143.ZHANG Yufeng，JIN Aidong.The existence and uniqueness of repairable system with a plurality of critical and non critical errors of the incomplete conversion of cold standby［J］.Mathematics in Practice and Theory，2004，34(12):137-143.(in Chinese)

［6］郭大钧，黄春潮，梁方豪，等.实变函数与泛函分析［M］.山东:山东大学出版社，2005.

［7］秦化淑，林正国.常微分方程及应用［M］.北京:国防工业出版社，1985:108-138.

［8］陈忠，宋杰.一类正则半群上的若干探讨［J］.贵州大学学报:自然科学版，2014，31(3):5-7.CHEN Zhong，SONG Jie.A class of regular semigroups［J］.Journal ofGuizhou University:Natural Science，2014，31(3):5-7.(in Chinese)