大地电磁静态效应模拟研究

时彬，郇恒飞，高铁，赵院东

1.辽宁省地质矿产调查院，辽宁沈阳 110031；2.中国地质调查局沈阳地质调查中心（沈阳地质矿产研究所），辽宁沈阳 110034

大地电磁静态效应模拟研究

时彬1，郇恒飞2，高铁2，赵院东2

1.辽宁省地质矿产调查院，辽宁沈阳 110031；2.中国地质调查局沈阳地质调查中心（沈阳地质矿产研究所），辽宁沈阳 110034

通过数值模拟分析模型宽度、厚度、埋深、电阻率等参数对视电阻率、视相位的影响，发现TM模式受静态效应影响严重；异常体产生的静态效应畸变随埋深变浅而增大，地表异常造成的畸变尤为严重；异常体与围岩的电阻率差异越大造成的静态效应越明显；相比厚度，同比改变异常体的宽度对视电阻率的影响更大.通过曲线拟合各参数与视电阻率的相关函数，估算参数计算异常体对视电阻率的影响程度，以达到改正的目的.

大地电磁；静态效应；数值模拟；对数相对误差

在大地电磁测量中，常遇到因地表异常或地形而产生静态效应［1］.正确认识静态效应，分析静态效应影响因素，定量地认识静态效应的影响量有利于更好地处理、解释大地电磁资料.笔者通过数值模拟分析静态效应影响因素，并从异常体的宽度、厚度、埋深、电阻率等方面进行模拟讨论，并以拟合曲线函数定量地总结各影响因素对静态效应的影响程度，以此作为地表地形、异常体产生静态效应的改正依据.

1 数值模拟

大地电磁数值模拟采用二维有限元数值模拟计算，每个剖分单元采用双线性差值进行差值求解［2-3］.

其中，u为Ex或Hx，Ω为二维求解区域.

TE模式中，上边界AB处离地面足够远，u为Ex，τ=1/（iωμ），λ=σ-iωε；

TM模式中，上边界AB在地面，u为Hx，τ=1/σ，λ= iωμ.

其中，ω为较频率，u为介质磁导率，σ为介质电导率，ε为介电常数，CD为下边界.

2 数值模拟程序验证

建立三层模型，模型结构见图1.数值模拟正演TE、TM模式视电阻率、视相位结果与解析解结果对比见图2、3.

图1 三层模型示意图Fig.1 Three-tier model diagram

图2 视电阻率曲线对比Fig.2 Comparison of apparent resistivity curres

图3 视相位曲线对比Fig.3 Comparison of apparent phase curves

两种模式视电阻率、视相位曲线一致性较好.通过结果计算得到，TE模式视电阻率误差为0.34%，TM模式误差为0.14%；TE模式视相位误差为0.16%，TM模式视相位误差为0.15%.证明程序计算正确精度较高.

3 静态效应数值模拟

建立三层模型如图1，在背景场基础上设定二维异常体规模为100 m×50 m，异常体位于地表，低阻异常体电阻率为10 Ωm，高阻异常体电阻率为30 000 Ωm.在地表异常体中心，得到TE、TM模式下的视电阻率、视相位曲线见图4～7.解析解为不存在异常体时的背景视电阻率、视相位曲线.

3.1 不同模式、不同性质异常体静态效应对比

图4 地表低阻异常视电阻率曲线对比Fig.4 Comparison of apparent resistivity curves of surface low resistance anomaly

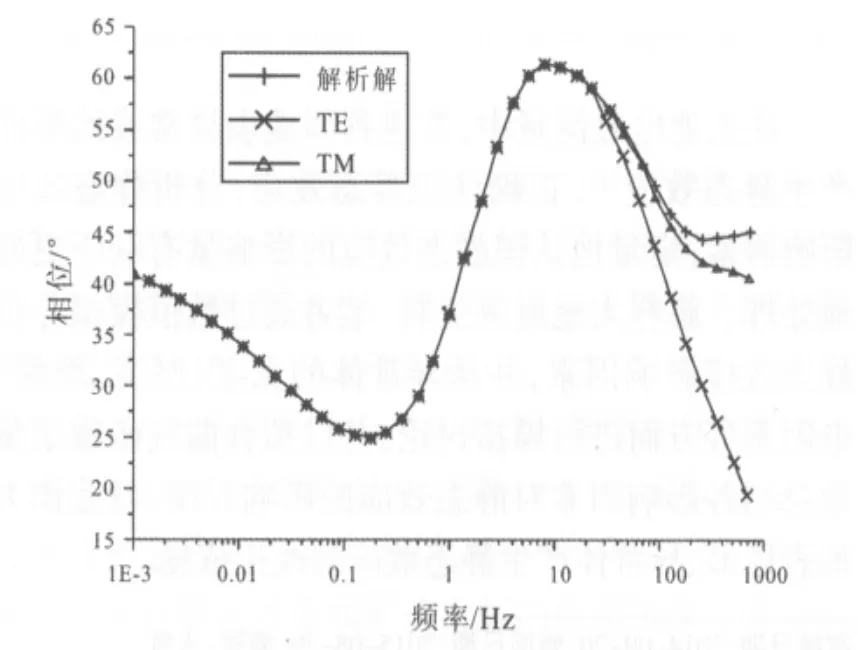
图5 地表低阻异常视相位曲线对比Fig.5 Comparison of apparent phase curves of surface low resistance anomaly

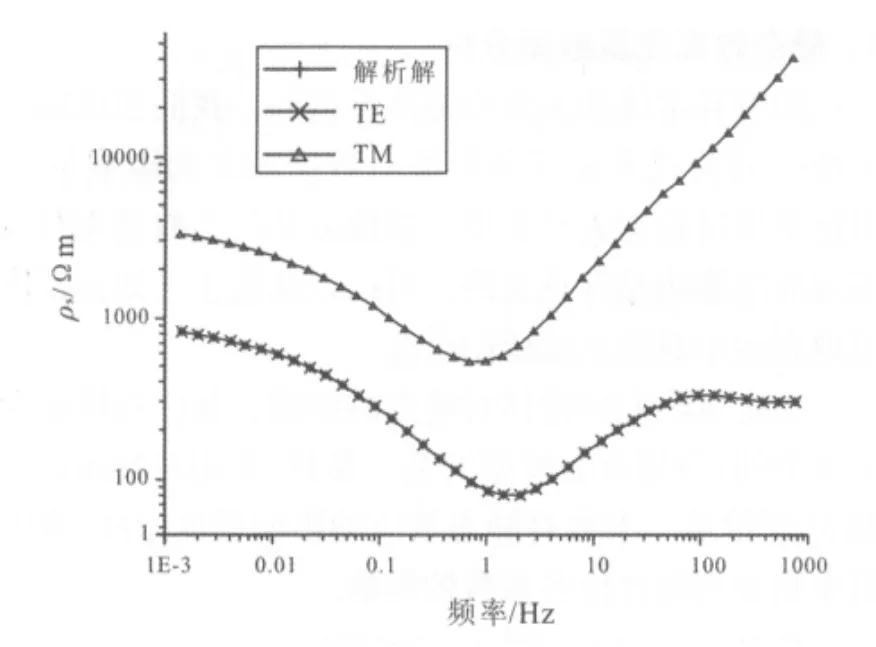
图6 地表高阻异常视电阻率曲线对比Fig.6 Comparison of apparent resistivity curves of surface high resistance anomaly

图7 地表高阻异常视相位曲线对比Fig.7 Comparison of apparent phase curves of surface high resistance anomaly

由图4～7可以看出，当地表存在异常体，TE模式视电阻率、视相位曲线与无异常体状态下的曲线基本一致，无明显数据畸变［4］；无论异常体为高阻还是低阻，TM模式视电阻率曲线出现严重的数据畸变，这个畸变可达几个数量级.TE模式对地表异常分辨率不高，受静态效应影响较小；而TM模式对水平方向电阻率分辨率较高，视相位也无明显畸变.在实际勘测中，TM模式更容易受到静态效应影响，而地表的低阻异常体引起的静态效应更为常见.下面主要分析TM模式下不同参数对视电阻率曲线的影响.

3.2 模型深度变化对静态效应的影响

背景三层模型和低阻异常体模型不变，只改变异常体顶端埋深H，得到视电阻率曲线如图8.

异常体埋深对视电阻率曲线影响很大，随着异常体埋深由深到浅，其静态效应逐渐增强，视电阻率曲线存在较大数值的平移；异常体埋深变化只会造成视电阻率曲线平移，基本不会改变形态；当异常体出露地表时，其造成的数据畸变程度会突然增大，这种畸变是数值计算造成的.

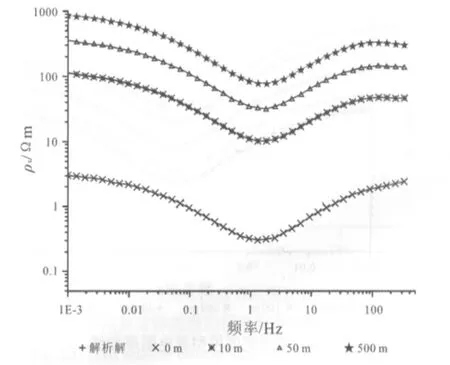
图8 不同深度异常体对视电阻率曲线影响Fig.8 Effect of anomalies with different depth on apparent resistivity

3.3 模型电阻率变化对静态效应的影响

为讨论异常体电阻率对静态效应的影响，将模型置于埋深100 m处，模型其他参数不变，改变模型电阻率，其视电阻率曲线对比见图9.

图9 不同电阻率异常体对视电阻率曲线影响Fig.9 Effect of anomalies with different resistivity on apparent resistivity

静态效应畸变程度与其异常体的相对电阻率差异RW/RY有关（RW为围岩电阻率，RY为异常体电阻率），相对电阻率差异越大，静态效应越明显，大的相对电阻率差异造成的数据畸变可达几个数量级.各频率对异常体反映程度基本相同.

3.4 模型宽度、厚度、大小对静态效应的影响

将模型置于埋深100 m处，模型其他参数不变，分别改变模型的宽度L、厚度d，等比增大模型规模，各参数影响的视电阻率曲线对比见图10～12.

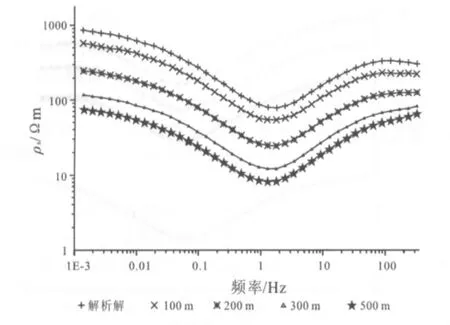
图10 不同宽度模型视电阻率曲线Fig.10 Apparent resistivity curves of models with different width

图11 不同厚度模型视电阻率曲线Fig.11 Apparent resistivity curves of models with different thickness

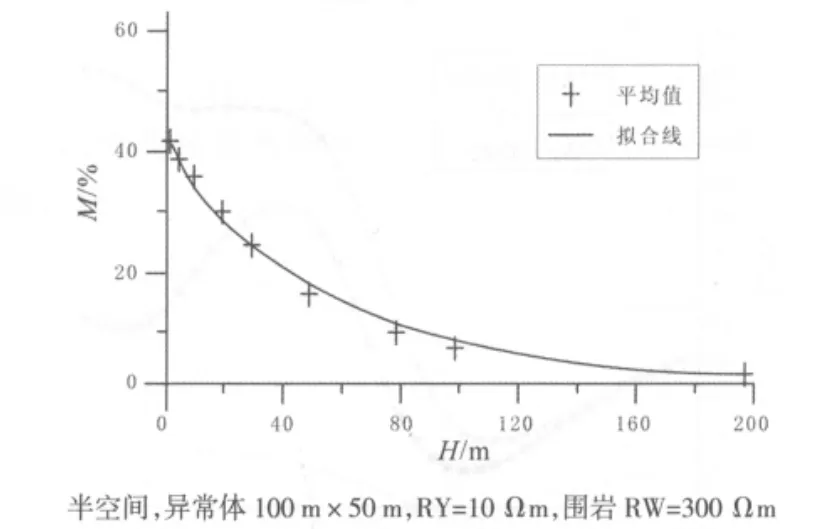
图12 不同大小模型视电阻率曲线Fig.12 Apparent resistivity curves of models with different size

从二维大地电磁模拟计算结果可以看出，异常体的宽度L和厚度d对视电阻率均有影响，宽度和厚度的增大均会造成静态效应畸变增强，但异常体的宽度d对TM模式视电阻率影响更大.在同比改变异常体规模时，模拟计算得到的视电阻率曲线形态发生变化.

4 静态效应定量数据分析

影响异常体静态效应是多参数的，我们很难用一个统一的公式来定义各参数对数据畸变的影响量［5］.但定量地讨论地表异常单一参数或某些参数变化对静态效应的影响是有意义的，可以以此改正已知异常体或地表地形对数据造成的畸变.

为定量研究异常体对畸变的影响，我们将模型置于半空间，分别改变模型的某一参数，采用对数相对误差M评价单一参数对静态效应的影响程度，并以视电阻率相对误差评价各参数的影响.

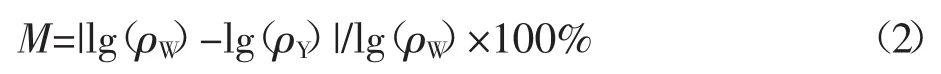
其中，ρY为存在静态效应时的视电阻率，ρW为无静态效应时的背景视电阻率.

图13 不同埋深的视电阻率对数相对误差Fig.13 Log relative error of apparent resistivity with different depth

4.1 异常体埋深对静态效应的影响

从前文的分析可以看出，同一异常体位于地下不同深度，对静态效应的影响程度差异很大.从图13可以看出，不同埋深异常体视电阻率对数相对误差偏差较小，证明引起静态效应的异常体在不同频率引起畸变的程度几乎相同.当异常体位于地表时，电阻率畸变陡增，且各频点影响程度有所不同；异常体位于地下，异常体不会改变视电阻率曲线形态，其对数相对误差可用拟合函数表示.在其他因素不考虑的前提下，异常体顶端埋深H引起静态效应畸变程度可用近似函数表示：

其中，ρY为存在静态效应时的视电阻率，ρW为无静态效应时的电阻率，H为异常体顶端埋深.

4.2 异常体相对电阻率对静态效应的影响

忽略其他相关因素，我们只考虑异常体电阻率对静电效应的影响.异常体产生的静态效应强弱与相对视电阻率的大小有关，异常体与围岩电阻率差值越大，其静态效应越强.当异常体其他因素不变，不同电阻率的异常体引起静态效应强度的相关关系见图14，可用函数（4）表示：

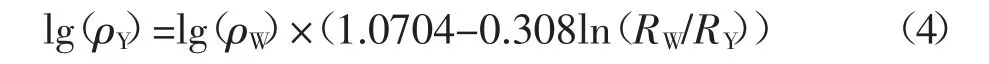
其中，ρY为存在静态效应时的视电阻率，ρW为无静态效应时的视电阻率，RW为围岩电阻率，RY为异常体电阻率.

图14 不同电阻率的视电阻率对数相对误差Fig.14 Log relative error of apparent resistivity with different resistivity

4.3 异常体规模对静态效应的影响

改变异常体的边长s，视电阻率对数相对误差变化规律见图15.无论异常体多大规模，静态效应都会存在，而且会影响各个频点；静态效应随s增大而增强.异常体规模对静态效应的影响不是递增的，当地质体增大到一定规模，对静态效应的数据畸变逐渐减弱，视电阻率值就会趋向于表现为他的真电阻率，在此不作讨论.

当异常体其他因素不变，不同电阻率的异常体引起静态效应强度可用函数（5）表示：

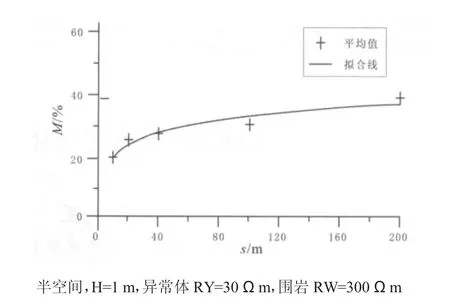
图15 不同异常体规模的视电阻率对数相对误差Fig.15 Log relative error of apparent resistivity with different anomaly size

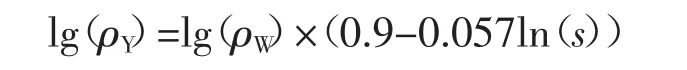
对于已知地表异常和地形引起的数据畸变，可用上述公式进行改正静态效应畸变.

5 结论

1）TE模式视电阻率和相位受到因异常体产生的静态效应影响较小；TM模式视电阻率受到高阻、低阻异常体静态效应影响较大.

2）异常体的埋深、与围岩的电阻率差值对静态效应影响较大，会造成视电阻率值数量级上的畸变.

3）通过数据分析拟合得到的函数可以定量地分析各参数对静态效应产生的影响，可以用于地表等已知异常体产生的静态效应校正.

［1］陈乐寿，王光锷.大地电磁测深法［M］.北京：地质出版社,1990.

［2］曾国.大地电磁二维有限元正演数值模拟［D］.长沙：中南大学,2008.

［3］朱威.二维大地电磁正反演人机交互解释系统研究［D］.长春：吉林大学,2009.

［4］陈辉，王春庆，雷达，等.CSAMT法静态效应模拟及其校正方法对比［J］.物探化探计算技术,2007,29（S1）:64—67.

［5］罗延钟，何展翔，马瑞伍，等.可控源音频大地电磁法的静态效应校正［J］.物探与化探,1991,15（3）:196—202.

STUDY ON THE SIMULATION OF MAGNETOTELLURIC STATIC EFFECT

SHI Bin1,HUAN Heng-Fei2,GAO Tie2,ZHAO Yuan-dong2

1.Liaoning Institute of Geological and Mineral Survey,Shenyang 110031,China; 2.Shenyang Institute of Geology and Mineral Resources,CGS,Shenyang 110034,China

With analysis on the effect of parameters such as model width,thickness,depth and resistivity on apparent resistivity and apparent phase by numerical simulation,it is found that the TM mode is seriously affected by static effect. The static distortion caused by anomalous bodies increases while the burial depth becomes shallow.The distortion caused by surface anomaly is particularly serious.The greater the resistivity difference between the anomaly and wall rock is,the more obvious its static effect is.Compared to thickness,the change of anomaly width has a greater effect on apparent resistivity.The correlation function between the parameters and apparent resistivity based on curve fitting is used to estimate the influence of anomalies on resistivity for the purpose of correction.

MT;static effect;numerical simulation;logarithmic relative error

1671-1947（2015）04-0373-05

P631.3

A

2014－09－20；

2015-08-29.编辑：张哲．

中国地质调查局项目“黑龙江多宝山白石砬子地区矿产地质调查”（［2015］02-08-01-021）.

时彬（1986—），男，硕士，从事地球物理勘查工作，通信地址辽宁省沈阳市皇姑区宁山中路42号羽丰大厦.

高铁（1983—），男，博士，工程师，从事重磁电理论及应用研究，通信地址辽宁省沈阳市皇姑区黄河北大街280号，E-mail//39085496@qq.com