基于正态分布和两参数威布尔分布的风速曲线拟合方法研究

张盼盼

(贵州大学，贵州 贵阳 550025)



基于正态分布和两参数威布尔分布的风速曲线拟合方法研究

张盼盼

(贵州大学，贵州 贵阳 550025)

以日常生活中常用到的正态分布和两参数威布尔分布拟合实际的风速数据，采用最大似然估计法得到两种分布的相关参数值，并在此基础上以这两种分布的概率密度函数和分布函数图与风速数据的频率直方图做对比，以此分析哪种分布函数模拟风速分布的效果比较理想，得到的结果是两参数威布尔分布可以认为是拟合风速较好的模型。

正态分布，两参数威布尔分布，概率密度函数

1 引言

风能作为风力发电的基础，以其清洁性和可再生性受到越来越广泛的应用。风速分布模型的确立，可以更好地进行配电网的可靠性评估和风电场的容量选址分析。但风能本身存在着间歇性和不稳定性的缺点使得风速也存在着不稳定性。因此有必要对风速的分布模型进行更进一步的研究。通常情况下描述风速分布模型的有瑞利分布、正态分布和两参数威布尔分布。瑞利分布因其应用于风速低于3.6m/s的范围内，且误差较大，所以瑞利分布不被认为是用来描述风速的理想分布模型。相比之下，正态分布和两参数威布尔分布应用则较广泛。国内对应用正态分布和两参数威布尔分布描述风速分布也做了一些研究。文献[1]认为当形状参数k>3.5时，风速的分布可以用正态分布来描述，并以正态分布建立风速负荷二元正态联合分布函数，并进一步评估配电网的可靠性。文献[2]比较了威布尔分布参数的三种算法，并以计算得到的三种参数值拟合风速曲线。文献[3]采用四种不同方法求取威布尔分布参数。文献[4]也采用三种算法求取威布尔分布参数，并应用威布尔拟合曲线分析希尼尔水库风能情况。文献[5]采用最大似然估计了对数正态分布的参数。上述文献只选择了一种分布模型去拟合风速曲线，但基于风速的时变性和各地情况的特殊性，本文以正态分布和威布尔分布这两种分布模型分别对风速进行拟合，对拟合的结果进行对比分析从而得到描述风速的理想分布模型。

2 正态分布模型

正态分布(高斯分布)是一种在工程领域中经常应用到的概率分布模型。假设变量X服从具有两个参数μ和σ2的正态分布，记X服从正态分布N(μ，σ2),那么此正态分布的概率密度函数为：

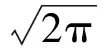
(1)

其中，参数μ为正态分布的期望，σ2为正态分布的方差。当μ=0，σ2=1时，称变量X服从标准正态分布。只有确定两个参数μ和σ2值后，风速的正态分布概率密度函数解析式才能唯一确定。常用的正态分布参数值估计方法有多种，本文采用最大似然估计法求取参数值μ和σ2。

3 威布尔分布模型

威布尔分布是目前被认为是描述风速分布比较理想的模型，它主要应用于可靠性分析中。威布尔分布的概率密度函数为：

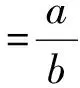
(2)

其中,参数a称为威布尔分布的形状参数，b称为威布尔分布的比例参数。以威布尔分布模拟风速分布时，首先要确定参数a和b的值。常用参数值的确定方法有HOMER软件法、最小二乘法和最大似然估计，本文同样采用最大似然估计威布尔分布参数值。

4 最大似然估计法

设X为总体，X1,X2,X3,…,Xn为来自的样本，x1,x2,x3,…,xn是相应于样本的一个样本值，那么X1,X2,X3,…,Xn等于x1,x2,x3,…,xn这个事件的概率为:

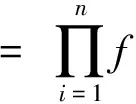
(3)

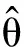
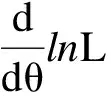
(4)

5 模型的建立

以某地一年风速数据为样本值输入matab中，采用最大似然估计法求得的正态分布的期望和方差值如表1所示，参数置信区间为90%。

表1 正态分布参数值

把表1数据代入公式(1)得到风速分布的正态分布模型解析式如公式(5)所示。

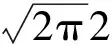
(5)

在matlab中输入风速数据，采用最大似然估计法求得威布尔分布的两个参数值a和b如表2所示，参数置信区间为90%。

表2 两参数威布尔分布参数值

(6)

6 风速曲线拟合仿真

根据公式(5)和(6)所确定的解析式拟合风速数据，通过matlab编制程序得到正态分布概率密度函数拟合曲线和威布尔分布概率密度函数拟合曲线如图1所示。

图1 正态分布和两参数威布尔分布概率密度函数图

正态分布函数拟合曲线和两参数威布尔分布函数拟合曲线如图2所示。

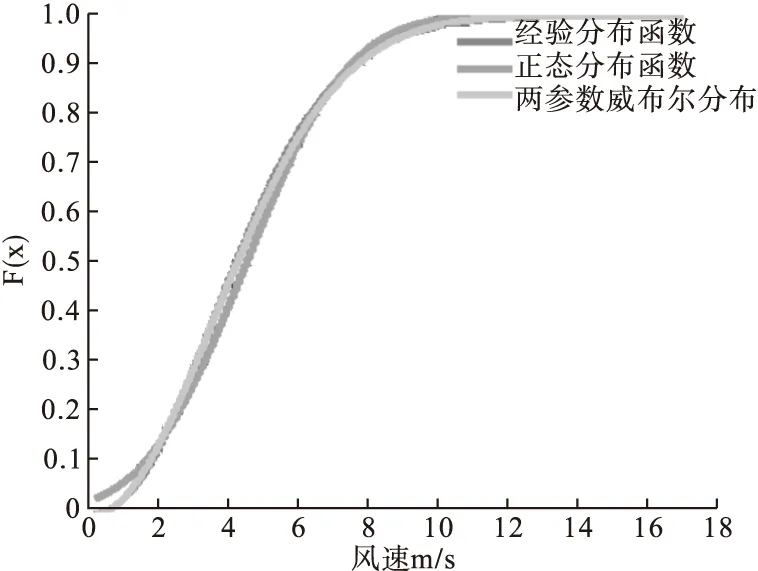
图2 正态分布和两参数威布尔累积分布函数图

从图2可以看出，两参数威布尔函数分布与样本的经验分布函数拟合的效果相对于正态分布函数拟合的效果要好。

7 结论

从本文所得结果可以看出，两参数威布尔分布可以认为是描述实际风速分布较好的模 型，采用最大似然估计法求取分布函数中的未知参数，这样可以减少采用其它方法所存在的计算工作量。从图中可见正态分布模拟风速分布曲线的误差还是比较大的，所以在通常情况下，我们采用两参数威布尔分布来模拟风速分布。风速分布模型的确立可以为含分布式电源的配电网可靠性分析提供依据，从而提高可靠性分析的准确度和可信度。

[1] 孙若笛.计及风速与负荷时序相关性的配电网可靠性评估[D].重庆:电气工程学院,2012.

[2] 徐卫民,孔森红,魏保玉.三种风速威布尔分布参数算法的比较[C]//第26届中国气象学会年会气候资源应用研究分会场论文集,2009：141-143.

[3] 包小庆,刘志强,吴永忠,等.双参数威布尔分布函数的确定及曲线拟合[J].能源与环境,2007：4-9.

[4] 魏光辉,申莲,何玉春.双参数威布尔分布函数在希尼尔水库风速资料分析中的应用[J].沙漠与绿洲气象，2008：38-39.

[5] 于洋,孙月静.对数正态分布参数的最大似然估计[J].九江学院学报,2007：55-57.

[6] 盛骤,谢式千.概率论与数理统计[M].北京:高等教育出版社,2008：152-153.

Research on the fitting Method of Wind Curves Based on Normal Distribution and Two Parameter Weibull Distribution

ZHANGPan-pan

(Guizhou University,Guiyang 550025,China)

Take normal distribution and two parameter weibull distribution in everyday life to fit actual wind speed data,adopt maximum quasi-nature method of estimation to get relevant parameters of the two kinds of distrubitions,and on the basis of this,compare the probability density function and distribution density arrangement of these two distributions with the frequency histogram of the wind speed data.For this reason,we analyze which distribution function simulation wind speed distribution is more ideal.The result is that two parameter weibull distribution is to be considered as the fitting wind speed model better.

normal distribution;two parameter weibull distribution;probability density function

1004-289X(2015)04-0047-03

TM61

B

2014-09-25