基于二代小波的表面粗糙度信息提取
2015-04-22王晓强李艳娜崔凤奎梅倩倩
王晓强,李艳娜,崔凤奎,梅倩倩
(河南科技大学 机电工程学院,河南 洛阳 471003)
基于二代小波的表面粗糙度信息提取
王晓强,李艳娜,崔凤奎,梅倩倩
(河南科技大学 机电工程学院,河南 洛阳 471003)
为了快速准确地提取表面粗糙度,提出一种用二代提升小波用于滤波的方法。基于提升理论,对信号进行分解与重构,构造提升小波滤波器。根据表面形貌的综合成分,构建零件表面形貌数学分析模型。基于模型构建原理对数学模型进行求解,基于Matlab进行滤波仿真,确定分解层数,选择合适滤波器,实现零件表面形貌中的表面粗糙度信息提取。研究结果表明:二代提升小波用于表面粗糙度信息的提取计算复杂度更低、速度更快,提取的信息更加精确有效。
小波变换;粗糙度模型;粗糙度提取
0 引言
零件表面粗糙度的优劣是评定机械加工零件微观表面质量的重要指标之一,在一定程度上影响着零件的技术性能和使用功能,决定了数值评定的精确度。因此,在数值评定之前将零件表面形貌进行分离,对零件表面的粗糙度信息进行提取有着十分重要的意义。
文献[1]提出了基于高斯滤波的稳健工程表面评定方法,消除表面异常值获得可靠的评定基准。文献[2]基于小波变换的研究,在说话人识别系统中提取反映说话人个性的语音特征参数。文献[3]提出了一种表面综合形貌误差的灰色分离法,提取各部分误差信息。文献[4]认为进化小波提升变换是适应于纳米级精度表面的表面导向频率分析、表面识别与重构。文献[5]研究了从数字激光散斑纹理图像中提取表面粗糙度的方法,通过对数字激光散斑纹理图像进行小波变换,建立纹理特征参数与表面粗糙度的关系,确定表面粗糙度。文献[6]阐述了采用小波多分辨分析的方法对工件表面几何形状误差信号进行分解的具体方法,一方面排除外界噪声对原始采样信号的干扰;另一方面从工件表面形貌综合误差信号中同时提取出了形状误差、表面波度及表面粗糙度。
目前,尽管小波技术发展迅速,但其基于傅里叶变换,小波构造形式不固定,算法结构复杂,提取出的粗糙度不够精确。需要更加准确快速地分离表面粗糙度,确定表面评定基准,以更精确评定表面粗糙度。
本文研究二代小波提升算法的理论基础,对实际中运用的传统算法进行提升运算,通过第二代小波变换对零件表面形貌信号进行分离,对信号数据进行实际分析,提高零件表面形貌信息的滤波性能,优化表面粗糙度信息提取的精度。
1 表面粗糙度提取的模型建立
1.1 二代小波变换(SGWT)原理
基于提升方案构造的二代小波变换是1994年Swelden提出的,对一代小波mallat算法进行提升,分为分解、预测、更新三大步骤。其使用空间变换的预测算子[7]和更新算子[8],构造双通道滤波器,实现可逆变换,如图1所示。
1.2 表面粗糙度模型

图1 提升算法的实现步骤
若粗糙表面轮廓为f(x),将f(x)看成信号的离散采样点,且假设f(x)为所能获得的轮廓表面最精细的综合形貌,它为表面粗糙度、波纹度、表面形状误差和工件形位误差等多种频率成分的综合。其中,表面粗糙度为高频信号,波纹度为中频信号,表面形状误差为低频信号。s2(x)表示轮廓粗糙度成分,s1(x)表示评定基准,是表面波纹度、轮廓表面形状误差之和,则表面粗糙度评定模型为:
f(x)=s1(x)+s2(x)。
(1)
若表面粗糙度与评定基准的分界频率为ω0,则s1(x)与s2(x)的频谱分别满足:

(2)
式中:s1(ω)、s2(ω)、f(ω)分别是s1(x),s2(x)、f(x)的Fourier变换。
1.3 数学模型的小波求解
数学模型的小波求解具体过程如下:
(Ⅰ)取c0,n=f(nT),其中,f(nT)(n=1,2,…,N)为工件轮廓的离散采样,T为采样间隔。
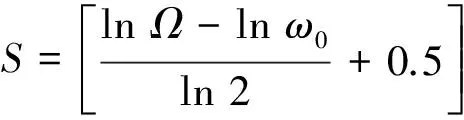
(Ⅲ)小波分解:
(3)

(Ⅳ)小波重构:

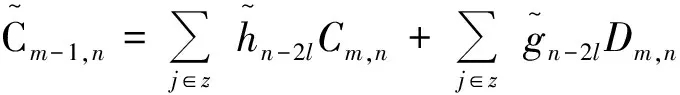
(4)
即得到一组C0,n(n=1,2,…,M)。
(Ⅴ)令f1(nT)=C0,n(n=1,2,…,M),得到小波评定基准的一组离散值。
(Ⅵ)令f2(nT)=f(nT)-f1(nT)(n=1,2,…,M),得到表面粗糙度信息。
在工程应用中,小波函数的选择必须满足连续、线性相位、紧支撑和正交性,以尽可能地保证滤波不失真,减少变换过程中的运算数据量,节省时间和空间。Daubechies系小波满足小波函数选择的所有原则,取Daubechies小波用于二代小波粗糙度信息提取,记为dbN,其中N为小波分解的尺度,可取为2,3,4,…,10。
2 实验验证
本实验采用6205轴承外圈原始表面轮廓,其内径尺寸为25 mm,对其进行采样。根据GB/T 3505—2000中表面粗糙度主要术语关于评定长度的规定,确定采样长度为0.5 mm,评定长度为5个采样长度即2.5 mm,取采样间隔0.05 s。通过采用泰勒-霍普森公司的白光干涉仪CCI6000对其进行测量,采集表面轮廓512个点,采集原始信号。
经过采样得到的原始信号如图2所示。样品表面经过磨削加工,其轮廓由形状误差、波纹度和粗糙度3部分组成。先对其进行去噪[9],得到去噪信号后进行分解,需确定各部分的分界频率,不同的分界频率对原始信号的分解次数不同,提取出的各频段成分也不相同,分界频率根据表面实际情况来取值。本文采用频谱分析法确定分界频率,即对原始信号进行频谱分析,得到原始信号频谱(如图3所示),以确定形状误差、波纹度和粗糙度的频率范围。

图2 原始采样信号图图3 原始信号频谱图
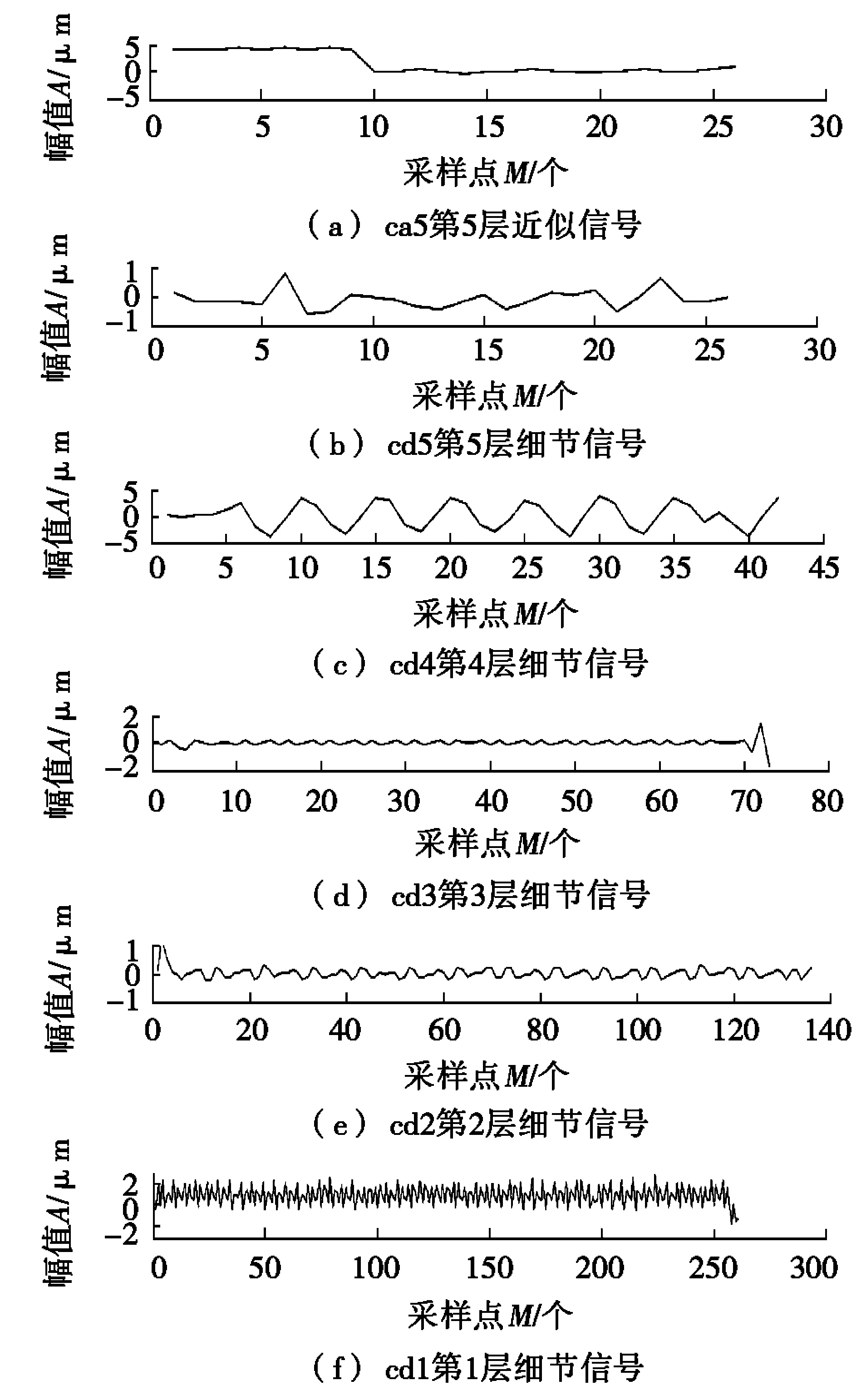
图4 提取各层的信号
根据得到的频谱图信息,确定其低频、中频和高频信号的分界频率分别为1 Hz、6 Hz和10 Hz,且表面形状保持了原始轮廓的基本形貌。信号的低频与中频的分界频率为1 Hz,采样频率为20 Hz,可以确定分解次数为5。根据提升小波变换原理进行编程,用db5小波函数对原始信号进行5次小波分解,并分别提取尺度5的低频近似信号与尺度1~5的高频细节信号,如图4所示。
在提取的各层信号中,ca为分解得到的信号近似成分,cd为分解得到的信号细节成分。由信号频率的组成部分和小波分解后各层频率的分布可知:高频位于cd1层,低频位于ca5和cd5层,中频位于cd2~cd5层。对信号进行重构(如图5所示),将采样点数M视为采样长度,幅值A视为表面轮廓,即可在图5中看到重构后的表面轮廓各频段波形。
图5a为重构后的低频形状误差,图5b为得到的中频波纹度,图5c为得到的高频粗糙度,对提取的表面综合形貌粗糙度轮廓算数平均偏差进行评定,得到Ra1=0.811 μm。
3 结果分析
以下对实验中的6205轴承外圈的表面轮廓进行误差分离,分别使用一代小波滤波和高斯滤波方法,并对结果进行比对分析,该轴承外圈经Taylor-hobson白光干涉仪测量得到的轮廓算数平均偏差Ra的值为0.8 μm。取样长度为0.25 mm,评定长度为5个取样长度(即1.25 mm),整个评定长度内取M个采样点(即512个)。
图6为用一代小波提取的评定长度内表面综合形貌的粗糙度轮廓算数平均偏差,其评定结果为Ra2。图7为用高斯滤波提取的评定长度内表面综合形貌的粗糙度轮廓算数平均偏差,其评定结果为Ra3。评定结果数值及其与Taylor-hobson白光干涉仪测量得到的轮廓算数平均偏差Ra相对误差,如表1所示。
得到的粗糙度轮廓算数平均偏差Ra1、Ra2、Ra3与Ra的相对误差均在2.5%的误差范围之内,说明本文所用的方法具有有效性。在精度上,小波滤波比高斯滤波提取的粗糙度信息的精度有效提升,而二代小波比一代小波提取的粗糙度精度虽提升不多,但是在速度上,高斯滤波依赖于傅里叶变换,计算复杂,小波滤波摆脱傅里叶变换。一代小波mallat算法db5小波进行20次乘法,18次加法;二代小波提升算法db5小波进行12次乘法,10次加法[10],速度提升将近一倍。
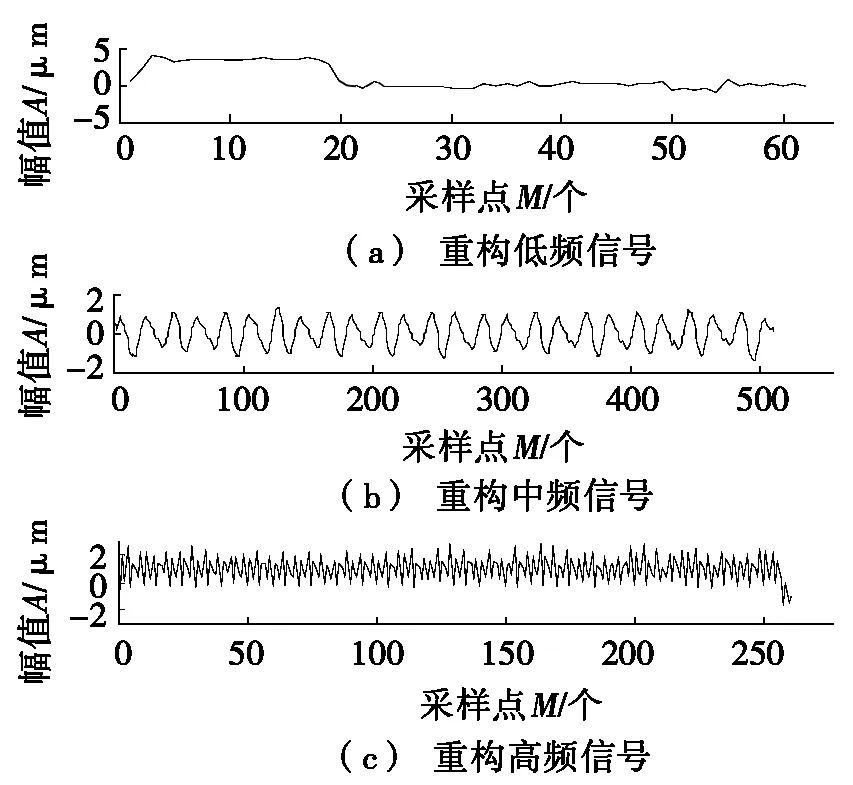
图5 用二代小波变换重构的信号
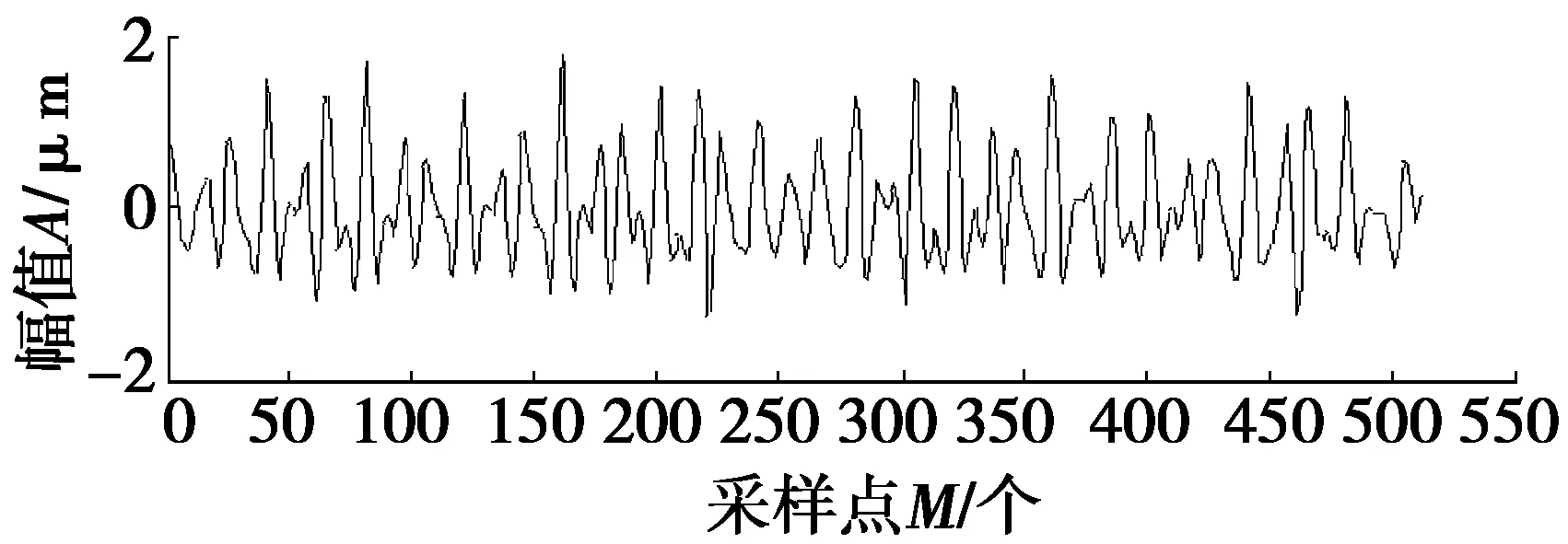
图6 用一代小波滤波提取的粗糙度信息
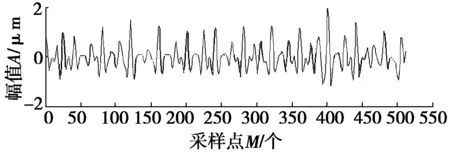
图7 用高斯滤波提取的粗糙度信息

表1 对标准样板提取的粗糙度精度对比
因此,采取本文中的方法,可对表面形貌进行不同尺度下的分析处理,分离出表面形貌各个频率成分,快速有效地实现表面形貌中的粗糙度、波纹度、形状误差的提取。
4 结束语
本文基于提升理论对二代小波算法进行提升,用于表面综合形貌误差信息的分离,可以快速有效地实现表面粗糙度信息提取。
(1)与传统的方法相比较,本文采用的提升格式摆脱了傅里叶变换的约束,是完全基于时域的双正交小波,具有固定的小波构造形式,并不需要知道尺度函数与小波函数表达式,所有的运算均在时域内进行,算法结构简单、速度快、占用内存少。
(2)建立粗糙度模型,并对其求解和编程。对原始采样信号进行频谱分析,确定各部分误差的分界频率。对采样信号进行分解,得到各尺度信号,提取得到轮廓各部分误差,其精度高于传统的方法,而且可以对复杂曲面的表面综合形貌误差进行分离和提取。
[1] 李惠芬,将向前,李柱.基于高斯滤波的稳健工程表面评定方法[J].华中科技大学学报,2002,30(8):43-45.
[2] 刘雅琴,周炜.基于小波变换的说话人语音特征参数提取[J].河南科技大学学报:自然科学版,2005,26(4):44-48.
[3] 王中宇,孟浩,付继华.表面综合形貌误差的灰色分离法[J].仪器仪表学报,2008,29(9):1810-1815.
[4] Jiang X,Scott P,Whitehouse D.Wavelets and Their Applications for Surface Metrology[J].CIRP Annals Manufacturing Technology,2008,57(1):555-558.
[5] 杨蕾,卢荣胜,雷丽巧.基于小波变换的散斑纹理表面粗糙度信息提取[J].电子测量与仪器学报,2012,26(12):1091-1095.
[6] 蔡改贫,谢文涓.基于小波变换的回转类零件圆度误差分离及其评定方法的研究[D].赣州:江西理工大学,2009.
[7] 段晨东,姜洪开,何正嘉.一种改进的第二代小波变换算法及应用[J].西安交通大学学报,2004,38(1):47-50.
[8] 严太山,崔杜武.求解无约束优化问题的知识进化算法及其收敛性分析[J].控制理论及应用,2010,27(10):1376-1382.
[9] 常宏韬,孟庆虎.基于小波变换的一种红外图像增强算法[J].河南科技大学学报:自然科学版,2015,36(1):48-51.
[10] 赵伟,邱隆伟,姜在兴,等.小波分析在高精度层序划分中的应用[J].中国石油大学学报,2009,33(2):18-22.
国家自然科学基金项目(51475146)
王晓强(1972-),男,山东莱州人,教授,博士,硕士生导师,研究方向为CAD/CAM、先进制造技术、精密测量技术.
2014-11-19
1672-6871(2015)03-0014-04
TH161.14
A
