Further results on stability of system with two additive time-varying delays

, ,



Further results on stability of system with two additive time-varying delays

SUHong,XUZhaodi,WANGTingting

This paper contributes to the study of stability of linear systems with two additive time-varying delays.In the case of linear systems, a lot of stability criteria have been proposed, which all are aimed to reduce the conservatism of stability systems.However, seldom have the existing methods contributed on the linear systems with two additive time-varying delays.In this paper, we first present an alternative inequality based on the reciprocally convex combination inequality and Park inequality.By designing an inequality technique, we can obtain a sufficient condition theorem and apply some existing methods to tractable LMI.Finally, time delay derivate by using our theorem is better than that of by using the existing ones under the same system.Numerical examples are presented to demonstrate the improved method is effective and feasibly.

two additive delay; linear matrix inequality; stability analysis

0 Introduction

During the past several decades, the stability of time delay systems have been widely applied in various practical systems, such as engineering systems, biology, economics, neural networks and so on.Since time delays are also the main reason of causing oscillation, divergence or instability.Considerable efforts have been made the stability for systems with time delays and many important results on the dynamical behaviors have been reported, the reader is referred to[1-5].The delay information of system stability criteria are divided into two categories: delay-independent stability criteria[6]and delay-dependent stability criteria[7].In the last decades, more attentions have been paid to delay-dependent stability of time-delay systems.Therefore, it is important to analysis the stability of delayed continuous system in the literature.

In the early time, researchers consider the following basic mathematical model[3-6]:

The same time , the Lyapunov-Krasovskii functional design which approaches in[11-15] do not make full use of the information aboutτ(t),τ1(t),τ2(t) which would be inevitably conservative to some extent.What is more, reducing conservatism is still remains challenging.

1 Model description and preliminaries

In this paper, we consider the following system with two additive time-varying delays:

Wherex(t)∈Rnis the state.AandAhare known system matrices of appropriate dimensions.τ1(t) andτ2(t) represent the two time-varying state delay and satisfying:

Therefore the system (1) can be rewritten under the condition (3) :

Lemma 1.For any vectorsa,b∈Rnand for any positive definite symmetric matrixX

±2aTb≤aTXa+bTX-1b

2 Application of the new inequality

The objective of this section is to provide an inequality based on lemma 1 and lemma 2.

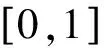
Then the following inequality holds:

3 Application to the stability analysis of time-varying delay systems

Theorem.For given scalars 0≤τ<∞, 0≤τ1<∞, 0≤τ2<∞,h>0,h1>0,h2>0, then the system (1) is asymptotically stable with delaysτ(t),τ1(t),τ2(t), if there exist positive matricesP,Qi(i=1,2,…,8) andRj(j=1,2,…,5), for any symmetric matricesS,U,T,W,V,Lwith appropriate dimension such that the following LMIs:

Where

Proof.We consider the following Lyapunov-Krasovskii function:

With

Taking the time derivative ofV(t,xt)

Where

Remark 1.It is vital to choice an appropriate LKF with the delay-dependent stability criterion.In order to demonstrate the effectiveness of corollary, we design the same LKF in the theorem.Furthermore, based on the proof, utilizing corollary of own, a sufficient asymptotic stability conditions are proposed in the theorem.

Remark 2.From the matrixΛof theorem, we can not only observe the relative betweenR1andR1,R2andR2,R3andR3,but also has a relationship betweenR1andR2,R2andR3,R1andR3.The new relationship will bring the new matrix element in the matrixΛ.Comparing with lemma 2, one case can demonstrate corollary of this paper is better than the method from lemma 2, and the case is that corollary.appears elementU,L,W,V, however, lemma 2 has nothing.Due to the new relationship, the matrix scaling with time delay information will be expand.So when the matrix multiply, it will be added to extra time-varying delay information items, then the information we can use will increase and LMIs solvable area will be expanded.

4 Illustrative example

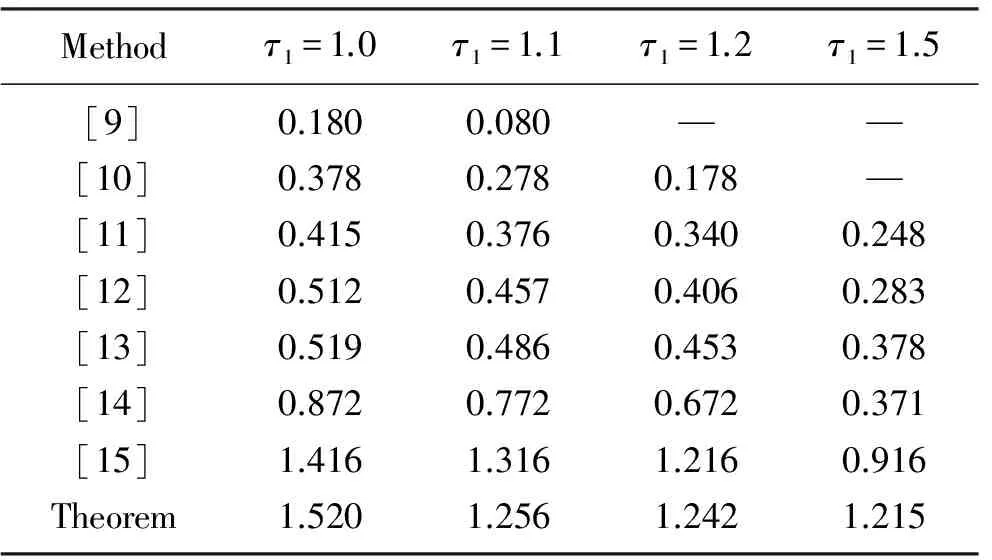
Table 1 Calculated delay bounds of τ2 for given delay bound of τ1

Fig.1 The dynamical behavior of Example for

5 Conclusion

In this paper, we first present an alternative inequality based on the reciprocally convex combination inequality and Park inequality.By designing the inequality technique, a sufficient condition theorem is provided.Finally, we proved effectiveness of the proposed approach and reduce the conservatism of stability systems than existing ones through numerical example.Furthermore, we propose the alternative inequality also adapt to the multi-relationship among metric and stability of the multi-delay system, and there is has certain reference value.

[1]YAKUBOVICH V A, LEONOV G A, GELIG A K.Stability of stationary sets in control systems with discontinuous nonlinearities[M].Singapore: World Scientific, 2004.

[2]LIN Chong, WANG Qingguo, LEE T.A less conservative robust stability test for linear uncertain time-delay systems[J].IEEE Trans Automat Control, 2006,51(1):87-91.

[3]HE Yong, WANG Qingguo, LIN Chong, et al.Delay-range-dependent stability for systems with time-varying delay[J].Automat, 2007,43(2):371-376.

[4]WU Min, HE Yong, SHE Jinhua, LIU Guoping.Delay-dependent criteria for robust stability of time-varying delay systems[J].Automat, 2004,40(8):1435-1440.

[5]FRIDMAN E, SHARKED U, LIU Kun.New conditions for delay-derivative-dependent stability[J].Automat, 2009,45(11):2723-2727.

[6]SUN Jian, LIU G, CHEN Jie, RESS D.Improved delay-range-dependent stability criteria for linear systems with time-varying delays[J].Automat, 2010,46(2):466-470.

[7]CHEN Peng, TIAN Yuchu.Delay-dependent robustH∞control for uncertain systems with time-varying delay[J].Inform Sci, 2009, 179(18):3187-3197.

[8]PARK P, KO J, JEONG C.Reciprocally convex approach to stability of systems with time-varying[J].Automat, 2011,47(1):235-238.

[9]WU Min, HE Yong, SHE Jinhua, LIU Guoping.Delay-dependent criteria for robust stability of time-varying delay systems[J].Automat, 2004,40(8):1435-1440.

[10]HE Yong, WANG Qingguo, XIE Lihua, et al.Further improvement of free-weighting matrices technique for systems with time-varying delay[J].IEEE Trans Automat Control, 2007,52(2):293-299.

[11]LAMA JAMES, GAO Huijun, WANG Changlong.Stability analysis for continuous systems with two additive time-varying delay components[J].System Control Lett, 2007,56(1):16-24.

[12]GAO H, CHEN T, LAM J.A new delay system approach to network-based control[J].Automat, 2008,44(1):39-52.

[13]DEY R, RAY G, GHOSH S, et al.Stability analysis for continuous system with additive time-varying delays: a less conservative result[J].Appl Math Comput, 2010,215(10):3740-3745.

[14]WU Haixia, LIAO Xiaofeng, WEI Feng, et al.Robust stability analysis of uncertain systems with two additive time-varying delay components[J].Appl Math Model, 2009,33(12):4345-4353.

[15]CHENG Jun,ZHU Hong.Improved delay-dependent stability criteria for continuous system with two additive time-varying delay components[J].Commun Nonlinear Sci Numer Simul, 2014(1):210-215.

[16]WANG Cheng, SHEN Yi.Improved delay-dependent robust stability criteria for uncertain time delay systems[J].Appl Math Comput, 2011,218:2880-2888.

1673-5862(2015)01-0038-05

(School of Mathematics and Systems Science, Shenyang Normal University, Shenyang 110034, China)

带有双时变时滞线性系统的稳定性分析

苏 宏, 徐兆棣, 王婷婷

(沈阳师范大学 数学与系统科学学院, 沈阳 110034)

研究了带有双时变时滞的线性系统的稳定性问题。在过去线性系统的研究成果中,学者提出了大量的时滞系统的稳定性条件,这些稳定性条件都是旨在减小稳定系统的保守性。从减小稳定系统的保守性出发,改变稳定性条件,首次提出了一种不同寻常的不等式方法,即结合相互凸组合不等式和Park不等式方法,设计了新的系统稳定性条件,来减小线性放缩时系统产生的保守性。然后,在提出的新不等式方法和线性矩阵不等式的解决方法基础上,给出了保持系统稳定的判据。最后,通过数值仿真例子阐述了在相同系统的条件下,利用定理的方法得到的时滞相比于现存方法更大,验证了改进方法的有效性和可行性。

双时滞; 线性矩阵不等式; 稳定性分析

TP391 Document code: A

10.3969/ j.issn.1673-5862.2015.01.009

Received date: 2014-05-28.

Supported: Project supported by National Natural Science Foundation of China(11201313).

Biography: SU Hong(1988-), female, was born in Anshan city of Liaoning province, master degree candidate of Shenyang Normal University; XU Zhaodi(1955-),male, was born in Anshan city of Liaoning province, professor and postgraduates instructor of Shenyang Normal University, doctor.