距离法定量评价储层地质模型的不确定性
2015-04-21戴危艳李少华刘诗宇
戴危艳,李少华,刘诗宇
长江大学地球科学学院,湖北武汉430100
距离法定量评价储层地质模型的不确定性
戴危艳,李少华,刘诗宇
长江大学地球科学学院,湖北武汉430100
针对目前常用的储层地质模型不确定性评价方法存在的主要问题,提出了先用距离函数计算模型之间的差异,再以差异的大小来判断不确定性大小的方法.以WZ油田西区为例,采用相控物性参数建模技术,利用顺序高斯模拟方法建立渗透率的三维模型.对各种度量差异的距离函数进行对比研究和分析,结果显示曼哈顿距离函数和欧氏距离函数能较好地刻画模型之间的差异.选用欧氏距离函数计算模型之间的差异,其原理是先计算每两个模型之间相对应的每一网格节点的渗透率值差的平方和,然后取平方根,得到一个表征各模型之间差异的矩阵.根据该矩阵可得到各个模型之间的差异程度,差异越大,不确定性就越大.最后通过对比模型过井剖面图分析结果与距离矩阵分析结果,说明了本方法的正确性,结果显示该方法能有效评价随机模拟生成的储层地质模型的不确定性.
储层地质模型;不确定性;距离函数;随机模拟;矩阵
0 引言
在油田开发过程中,从初期的储层地质基础研究到建立三维静态储层地质模型都包含许多不确定性[1-4],这些不确定性将直接影响油田开发方案的制定.如何定量评价这些不确定性是目前国内外研究的热点.传统评价地质不确定性的主要方法有概率理论和地质统计学,模糊数学适合评价地质不确定性.模糊集与其他评价不确定性的方法相比,最大的优点是可以以透明的方式表达任何概率下不确定性[5].单相三维流线模拟技术能评价储集层的连通性,以地质储量和可驱替储量为定量指标的三维储层地质模型不确定性评价.该方法结合了实验设计、响应曲面拟合和蒙特卡罗法等数学方法,能够对三维储集层地质模型的不确定性进行科学、有效的评价[6].储量历史拟合的方法能评价所建模型的不确定性[7].这些方法能够对三维储集层地质模型的不确定性进行科学、有效的评价,唯一的缺点是它们都是以模型所计算的储量为指标来评价模型的不确定性.而模型之间的差异体现在每一个网格的差异上,也就是说只有两个模型中每一网格所对应的属性模拟值都相差不大,这两个模型才是相似的.虽然计算储量时所用的是模型中每一网格的属性值,但并没有考虑网格与其所表示的属性模拟值大小的一一对应关系.这意味两个完全不同的模型,只要所有网格的属性值的和相等,储量的计算结果就是一样的,所以用这些方法来评价的模型的不确定性可能并不可靠.距离法通过距离函数测量任意两个模型之间的相异性,根据所建模型之间的差异来判断不确定性的大小,操作简单、速度快,不仅能够评价孔隙度模型、含水饱和度模型和NTG模型的不确定性,也能评价渗透率模型和相模型的不确定性.本文以50个渗透率模型为实例进行计算,通过对比模型过井剖面图分析结果与距离矩阵分析结果来验证本方法的正确性.
1 基本思路
采用相控物性参数建模技术,利用顺序高斯模拟方法建立渗透率的三维模型,将各个模型的渗透率数据提取出来,作为度量模型相异性的原始数据;常用的度量相异性的距离函数有欧氏距离、马氏距离、切比雪夫距离、曼哈顿距离、明考斯基距离等等,对各类距离函数进行对比研究,从中选出能刻画模型差异的函数;通过所选的距离函数计算这些模型两两之间的距离,得到一个相异性矩阵,根据该矩阵即可评价所建模型的不确定性,距离越大,表示模型之间的差异越大,意味着模拟结果的不确定性也就越大.
2 应用实例
以WZ油田西区为例,该区目前有5口开发水平井,1口裸眼井和1口探井,平均井距为400 m左右.目的层角二段是基底隆起背景上形成的披覆背斜构造,构造走向近于东西,地层倾角小,闭合幅度低,圈闭面积大,断层少,构造比较完整.沉积相储层为一套滨海砂岩沉积,岩性以长石石英砂岩为主,砂岩粒级多为细砂,在油田范围内厚度为110~130 m.
2.1 构建模型
在相控约束的基础上,运用序贯高斯模拟建立渗透率的三维模型.为了满足对模型的精细要求,本文的模型采用平面上25 m×25 m,垂相上的网格厚度为0.5 m,最终网格量达到近210万.图1是从生成的50个模型中随机选出的4个模型,直接观察这4个模型,显然无法准确识别出各个模型之间的差异大小.而通过距离函数,可计算任意两个模型对每一点处渗透率模拟结果的差异,将差异累加可得到一个相异性矩阵,这样可以更直观地识别模型的不确定性.
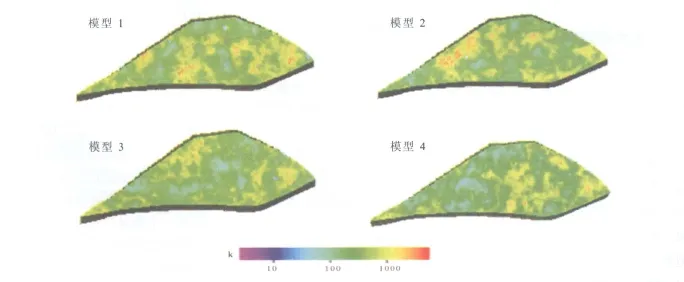
图1 序贯高斯模拟生成的4个渗透率模型Fig.1 Four permeability models generated by SGS
2.2 距离函数选取
度量相异性的距离函数有很多,如欧氏距离、马氏距离、切比雪夫距离、曼哈顿距离、明考斯基距离等等[8].下面分别对这些距离函数进行介绍,公式中i和j分别表示两个模型;n为模型网格总数;xin和xjn为这两个模型第n个网格的属性值大小,可以为属性值(如渗透率)的大小或其他一些特征值的大小;xi和xj分别为模型i和模型j的n个网格的属性值组成的向量;S为属性值的协方差矩阵;k表示模型的第k个网格.
2.2.1 欧氏距离
欧氏距离也称欧几里得距离,它是在m维空间中两个点之间的真实距离.在二维和三维空间中的欧氏距离的就是两点之间的距离[9-11].其计算公式为:

该公式的原理是先计算两个模型之间相对应的每一网格的属性值差的平方和,然后取平方根得到的结果即为两个模型的欧氏距离.欧氏距离是两个模型所对应的每一网格的属性模拟值的差异的累加,可以用该距离函数来刻画模型的差异.
2.2.2 马氏距离
马氏距离函数计算的是样本的协方差距离,与欧氏距离相比,马氏距离考虑了变量之间的相关关系,适合于多元或多因素的求异[12-13].其计算公式为:
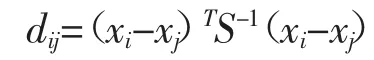
由于模型是随机生成的且模拟的是同一类属性,所以两个模型的属性值之间是没有相关性的,这表示公式中的协方差矩阵为单位矩阵,此时所计算的马氏距离实质上就是欧氏距离.
2.2.3 切比雪夫距离
切比雪夫距离是向量空间中的一种度量,它定义两个点之间的距离为其各坐标数值差的最大值[14].用它来计算模型之间的差异时,计算公式可写成:

该方法首先要将两个模型所对应的每一网格的属性模拟值的差异计算出来,然后取出最大值就是模型的切比雪夫距离,这个距离表示的只是两个模型中相对应的两个网格的属性模拟值的差异,并不能代表这两个模型整体的差异.
2.2.4 曼哈顿距离

曼哈顿距离来源于城市区块距离,是将多个维度上的距离进行求和后的结果[15-16].计算公式为:该方法度量模型之间差异的原理是,首先计算两个模型之间相对应的每一网格的属性值差的绝对值,然后将所有网格的属性值差的绝对值进行累加,即可得到两个模型之间的曼哈顿距离.与欧氏距离函数一样,曼哈顿距离函数的计算结果也是两个模型之间相对应的每一网格的属性值差异的累加,该距离函数也可用来刻画模型的差异.
2.2.4 明考斯基距离
明考斯基距离又称闵可夫斯基距离,是欧氏空间的一种测度,被看做是欧氏距离和曼哈顿距离的一种推广[17-19].其计算公式为:
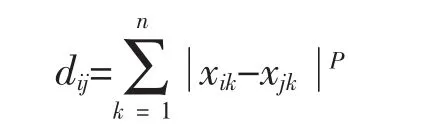
其中P是一个正整数,表示两点间的权,当P取1或2时的明氏距离是最为常用的,P=1即为曼哈顿距离,P= 2即为欧氏距离.当P取无穷时的极限情况下,可以得到切比雪夫距离.
用随机模拟所构建的属性模型是对整个研究区储层物性的预测,研究区的地理坐标与模型中网格的坐标是相对应的,在实际的地质研究中,每个地方的属性值都会对流体的储存及运移造成影响,所以,在刻画模型整体的差异时,必须将每个网格都考虑进去,因此两个模型之间的整体差异应该是两个模型所对应的每一网格的属性模拟值的差异的累加.根据上面所列出的各距离函数的公式可知,用欧式距离函数和曼哈顿距离函数都能较好地刻画模型之间的差异.本文以欧氏距离函数为例对模型差异进行刻画.
2.3 模型的不确定性评价
由于精细模型其网格数量太大,所以为了方便计算,将模型进行了粗化,粗化后网格数量为13万左右.用欧式距离函数计算模型之间距离时,其结果常常受比例尺选择、位移和旋转的影响[20].为了削弱这些影响,在构建距离矩阵之前,首先要对数据进行标准化处理,将渗透率值转化为无量纲的纯数值.数据处理完成后,在SPSS软件中选用欧氏距离函数计算这些模型两两之间的距离,得到一个差异性矩阵.如表1所示,该矩阵包括任意两个模型之间的距离,矩阵具有自相似性和对称性特征,即模型1与模型1之间的距离为0,模型1与模型2之间的距离等于模型2与模型1之间的距离.由该矩阵可以看出,各个模型之间的差异在100到150,这表示模拟结果的不确定性较大.造成这种情况的原因有很多,如选取的模拟算法有误、资料不完整、构造模型或相模型存在不确定性等.

表1 相异性矩阵(部分)Table 1 Dissimilarity matrix(part)
分析上面的矩阵可知,在编号1~10的模型中,模型1与模型2的差异最大,与模型3的差异最小,模型1的平均渗透率值为831 μm2,模型2的平均渗透率值为900 μm2,模型3的平均渗透率值为820 μm2,模型4的平均渗透率为805 μm2,模型5的平均渗透率为813 μm2,模型6的平均渗透率为817 μm2.图2是6个不同渗透率模型过井WZ12-8-1的剖面图,根据该图可以看出模型1与模型3的差异最小,其次是模型6、模型5、模型4和模型2,与距离矩阵分析的结果相对应,所以用距离法来评价储层地质模型的不确定性得到的结果是可靠的.
3 结论
由于资料的不足以及储层的非均质性,用随机建模方法所建立的储层地质模型存在不确定性.通过计算模型之间的差异,可以有效地认识模型的不确定性.相对于目前常用的不确定性评价方法,应用距离法评价模型不确定性的方法具有以下优点:首先,它相对客观,能根据两个模型中每个网格节点之间差异计算出两个模型整体的差异;其次,该方法操作简单、速度快,实现起来很容易;此外,该方法还避免了主观评价模型不确定性造成的偏差.
[1]Singh V,Hegazy M,Fontanelli L.Assessment of reservoir uncertainties for development evaluation and risk analysis[J].The Leading Edge, 2009,28(3):272—282.
[2]Manceau E,et al.Uncertainty management:From geological scenarios to production scheme optimization[J].Journal of Petroleum Science and Engineering,2004,44(1):11—25.
[3]李少华,张昌民,彭裕林,等.储层不确定性评价[J].西安石油大学学报:自然科学版,2004,19(5):16—24.
[4]吴胜和,杨延强.地下储层表征的不确定性及科学思维方法[J].地球科学与环境学报,2012,34(2):72—80.
[5]Bárdossy G,Fodor J.Evaluation of uncertainties and risks in geology:New mathematical approaches for their handling[M].Springer,2004.
[6]霍春亮,刘松,古莉,等.一种定量评价储集层地质模型不确定性的方法[J].石油勘探与开发,2007,34(5):574—579.
[7]Yang C,Nghiem L X,Card C,et al.Reservoir model uncertainty quantification through computer-assisted history Matching[C]//SPE Annual Technical Conference and Exhibition.Society of Petroleum Engineers,2007.

图2 过WZ12-8-1井的6个模型剖面图Fig.2 Profiles of six models for well WZ12-8-1
[8]贺玲,吴玲达,蔡益朝.高维空间中数据的相似性度量[J].数学的实践与认识,2006,36(9):189—194.
[9]Scheidt C,Caers J.Representing spatial uncertainty using distances and kernels[J].Mathematical Geosciences,2009,41(4):397—419.
[10]Carter R L,Morris R,Blashfield R K.On the partitioning of squared Euclidean distance and its applications in cluster analysis[J]. Psychometrika,1989,54(1):9—23.
[11]Caers J.Modeling uncertainty in the earth sciences[M].John Woiley&Sons,2011:1—229.
[12]宋运红,李振祥,孙连辉,等.马氏距离与欧氏距离方法在地球化学异常处理中的对比[J].吉林地质,2008,27(4):117—120.
[13]易丽华,朱德森.浅析一种基于Mahalanobis距离的色差检测方法[J].科学技术与工程,2003,3(4):364—366.
[14]邵昌升,楼巍,严利民.高维数据中的相似性度量算法的改进[J].计算机技术与发展,2011,21(2):1—4.
[15]苑津莎,李中.基于形状相似距离的K-means聚类算法[J].华北电力大学学报,2009,36(6):98—103.
[16]宋伟,刘洪亮,纳鹏宇,等.相似性测度函数分析及其在图像匹配中的应用研究[J].中央民族大学学报:自然科学版,2014,23(1):44—49.
[17]刘文军,游兴中.一种改进的凝聚层次聚类法[J].吉首大学学报:自然科学版,2011,32(4):11—14.
[18]马建华,李本星,黄静,等.基于Minkowski距离最小化的多模态图像配准[J].电路与系统学报,2008,13(5):48—52.
[19]HUANG Guo-shun,LIU Yun-sheng,WANG Xiang-dong.Some new distance between intuitionistic fuzzy sets[C]//Proc of the Fourth International Conference on Machine Learning and Cybernetics, Guangzhou,2005.
[20]曾广周.论数据标准化在聚类分析中的应用[J].山东工业大学学报,1988,18(1):21—26.
QUANTITATIVE EVALUATION ON THE UNCERTAINTY OF RESERVOIR GEOLOGICAL MODEL WITH DISTANCE METHOD
DAI Wei-yan,LI Shao-hua,LIU Shi-yu
School of Geosciences,Yangtze University,Wuhan 430010,China
Aiming at the main problems in the common evaluations on the uncertainty of reservoir geological model,this paper presents a method to calculate the differences between two models with distance function,then estimate the degree of uncertainty based on the differences.Taking the western WZ Oilfield for example,the facies-controlled physical parameters modeling technology and sequential Gauss stimulation method are used to establish 3D permeability models.Comparing and analyzing various distance functions,the results show that the Manhattan and Euclidean distance functions can describe the differences between models better.The principle of Euclidean distance function is calculating the quadratic sum of permeability value in each grid node between two models first,and then taking the square root to get a dissimilarity matrix characterized the differences between models.The difference between models can be directly obtained with the matrix:The greater the difference between models is,the greater the uncertainty of simulation result is.Finally,the comparative analysis results of intersection map and distance matrix show that this method is effective in evaluation of the uncertainty of reservoir geological model generated by stochastic simulation.
reservoirgeologicalmodel;uncertainty;distancefunction;stochasticsimulation;matrix
1671-1947(2015)05-0478-05
TE19
A
2015-01-12;
2015-05-08.编辑:张哲.
国家自然科学基金(41272136)和非常规油气湖北省协同中心创新基金(HBUOG-2014-14).
戴危艳(1991—),女,在读硕士研究生,研究方向为地质建模和油藏描述,通信地址湖北省武汉市蔡甸区大学路特1号(长江大学武汉校区),E-mail//879573435@qq.com
李少华(1972—),男,博士,教授,主要从事地质统计学、地质建模方面的研究与教学工作,通信地址湖北省武汉市蔡甸区大学路特1号(长江大学武汉校区),E-mail//jpishli@163.com
