中国城市效率与城市规模研究

金晓雨　郑军

摘要：用DEAMalmquist方法测算2000年和2010年中国209个地级市市辖区的城市效率，用非参数方法估计了我国城市效率在不同规模城市间的分布，并实证了城市效率变化的机制。研究发现：2000～2010年我国城市最优规模从350万人增加至717万人，增长10486%，而城市规模均值仅增长5047%，城市集聚不足的情况加剧，城市效率整体下降；城市效率变化和城市规模呈U型曲线关系，处于544万左右的城市效率降低最快，改善基础设施有利于提高城市效率；半参数估计表明计量设定和回归结果是稳健的。

关键词：城市效率；城市规模；DEA；非参数估计；半参数估计

DOI：10.13956/j.ss.1001-8409.2015.03.23

中图分类号：F061.5；F292 文献标识码：A文章编号：1001-8409（2015）03-0107-04

长期以来，我国城市发展政策是“严格控制大城市规模，合理发展中小城市，积极发展小城镇”。然而，国内外大量研究发现我国城市规模偏小，城市效率不高[1，2]。事实上，城市最优规模并不是静态的，不同历史时期在不同的城市体系下最优规模也会不同。那么，最近十年我国城市最优规模如何变化的？哪些因素决定了城市效率的变化？这对于制定未来城市发展政策具有重要意义。

对于我国城市效率的研究，大量文献使用多种方法计算了城市效率，但由于采用的方法、选择的样本城市和计算期不同，结果差异很大[3～5]。更重要的是，迄今尚无文献对城市最优规模的变动及城市效率变化的机制进行实证研究。城市是否有效率是判断我国城市是否达到最优规模的标准，为了分析我国城市最优规模的变化，需要计算城市效率的分布和演变机制，进而得出城市最优规模，并探寻提高城市效率的途径。为此，本文在以下方面进行研究：第一，用DEA方法测算了城市效率，首次使用非参数方法估计城市效率在不同规模城市间的分布，得出城市最优规模；第二，实证检验城市效率变化的影响因素，发现城市效率变化和城市规模之间呈U型曲线关系，基础设施对提高城市效率有显著作用，从机制上解释了城市效率的演变；第三，使用半参数回归对模型设定进行稳健性检验，为城市效率的实证研究提供新的思路。

1研究方法与数据说明

11研究方法

DEA是由Charnes等提出的衡量决策单元相对效率的分析工具，该方法基于线性规划的方法旨在寻找由样本中决策单元（Decision Making Unit，简称DMU）的生产结合所构成的最小凸锥，该凸锥的边界就构成了生产的技术前沿[6]。把每个决策单元的生产集和技术前沿进行比较，就可以得出该决策单元的技术效率。本文衡量城市效率采用的是基于投入的方法，在不变规模报酬假设下，其具体表达形式如下：

minθ，λθ

st.-yi+Yλ≥0

θxi-Xλ≥0

λ≥0 （1）

不变规模假设仅仅在所有决策单元都处于最优规模时才适用。对于城市而言，可能存在如人口流动限制、政策差别等因素使得城市并不处于最优规模[2]。Banker等将规模报酬不变的假设扩展到规模报酬可变，当决策单元并非处于规模报酬最优时，可以将技术效率分解为纯技术效率和规模效率[7]。用公式表示为：

技术效率=纯技术效率×规模效率 （2）

由于不同年份所构成的生产前沿不同，跨期不可比较，为了得到不同年份城市效率的变化，采用Malmquist分解方法，具体形式如下：

m0（yt+1，xt+1，yt，xt）=dt0（xt+1，yt+1）dt0（xt，yt）

×dt+10（xt+1，yt+1）dt+10（xt，yt）1/2（3）

如果该指数大于1，则代表城市效率较上一年度有所增长；小于1则有所下降；等于1说明没有变化。

12指标和数据来源

本文研究对象或决策单元是中国地级及以上城市的市辖区，城市效率的计算时期为2000～2010年。决策单元的生产集由单个产出和两种投入构成，城市的产出选择城市实际GDP衡量，投入选择城市资本存量和人口两个指标。由于没有各个城市的GDP缩减指数，因此将各城市名义GDP按照全国的GDP缩减指数折算为2000年为基期的实际值。资本存量采用张军等的永续盘存法[8]，选择2000年为基期，折旧率为10%。人口数据为城市市辖区常住人口，按照市辖区所辖各区常住人口加总得到。

计算城市效率的数据来源于《新中国城市统计50年》、《中国城市统计年鉴》、《中国统计年鉴》和《人口普查分县资料》。

2我国城市效率分布

用DEA方法估计了城市效率及其分解后的纯技术效率和规模效率，并用各个效率指标分别对城市规模进行非参数估计，得到拟合值如图1所示。图12010年城市效率与城市规模关系

注：图中技术效率、纯技术效率和规模效率分别表示2010年城市技术效率、纯技术效率和规模效率的非参数估计值，考虑到非参数估计存在边界效应，数据剔除城市规模5%和95%分位数之外的数据从图1可以看出，城市效率和城市规模总体上呈正相关关系，当城市规模达到717万人时，城市效率达最高。这和城市经济学理论预期一致，反映了大城市具有更高的净规模经济，同时也说明我国中小城市集聚不足。为了进一步分析城市效率的影响因素，将城市效率分解为纯技术效率和规模效率，纯技术效率和城市规模呈现微弱的U型曲线关系；规模效率和城市规模呈现倒U型关系，这和Au和Henderson的发现一致[2]。随着城市规模的增加，外部规模经济增速超过拥挤成本，净规模经济快速提高，但当城市规模达到最优后，拥挤成本增速会超过外部规模经济增速，使得净规模经济缓慢下降。比较城市效率和规模效率可以发现，受规模效率增速下降影响（相关系数为050）特大城市效率随着规模增加而增速放缓。

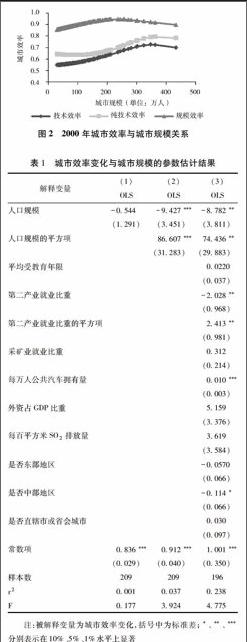
为比较2000～2010年间我国城市效率分布的演变，本文计算了2000年的城市效率，并绘出城市效率和城市规模的非参数估计结果（图2）。图2中2000年城市效率和分解后的纯技术效率、规模效率总体趋势同2010年类似。城市效率和城市规模呈倒U型曲线关系，城市最优规模为350万人。图22000年城市效率与城市规模关系

比较2010年和2000年的城市效率分布可以发现，2010年城市最优规模（717万）相对2000年城市最优规模（350万）提高了10486%，而同期我国城市规模增长平均只有5047%，城市集聚不足的情况在继续加剧，导致我国城市效率整体下降。

3我国城市效率的演变机制

城市效率在不同规模城市间的分布反应了特定时点不同规模城市的静态效率。从2000～2010年间城市静态效率的分布可以看出，城市静态效率的分布在不同时期会发生变化，那么城市效率的分布是如何变化的？什么因素影响了城市效率分布的变化呢？

为了分析2000～2010年间我国不同规模城市效率的变化，利用DEAMalmquist分解得到2000～2010年城市效率的动态变化，用城市效率变化对城市规模进行计量回归，同时控制影响城市效率的其他因素。设定计量模型如下：

tfpchi=β0+β1scalei+β2scale2i+Xiγ+εi （4）

式（4）中tfpchi代表城市i的效率变化，scalei代表城市常住人口规模，scale2i为城市常住人口规模的平方项，X为影响城市效率变化的其他因素，εi为扰动项。关注参数β1和β2的符号和显著性，而控制变量中变量的显著性则代表哪些因素会影响城市效率变化。

31变量选取和数据来源

计量回归所采用的被解释变量是Malmquist分解计算得到的城市效率变化，解释变量是城市规模。考虑到城市效率变化还会受其他因素的影响[2，9]，因此加入城市的初始特征控制变量，包括市辖区常住人口的平均受教育年限、代表产业结构的第二产业就业人数占总就业人数比重、采矿业就业比重、人均公共汽车拥有量、单位面积SO2排放量、市场开放度、东部城市虚拟变量、中部城市虚拟变量和直辖市或省会城市虚拟变量。本文计量回归所采用的数据来自2000年《中国人口普查分县资料》和《中国城市统计年鉴》。

32回归结果分析

表1列出了城市效率变化与各城市初始特征的回归结果。第一列只加入人口规模变量，回归系数不显著，第二列加入人口规模的平方项后，一次项和二次项回归系数均变显著，说明城市效率和城市规模并非简单的线性关系，而是呈现U型曲线关系，曲线最低点位于城市人口规模544万处。第三列加入相关控制变量，只有第二产业就业比重、东部地区虚拟变量和代表基础设施水平的每万人公共汽车拥有量的符号是显著的，其中基础设施水平在1%的水平上显著为正，改善城市基础设施水平有利于提高城市效率。

表1城市效率变化与城市规模的参数估计结果

33稳健性检验

城市规模经济和拥挤成本的产生和城市规模的关系复杂，城市动态效率和城市规模可能并非简单的线性或U型曲线形式。对于模型函数形式的误设会使得估计结果产生偏误。而非参数和半参数估计可以避免函数形式误设问题，根据数据更加灵活估计出变量之间的关系。半参数局部线性模型将部分已知函数形式的变量参数化，而不预设未知函数形式的变量，从而避免非参数估计的“维度诅咒”问题，并且更贴近现实。为此，设定半参数局部线性模型如下：

tfpchi=gscalei+Xiβ+μi （5）

式（5）中tfpchi代表城市i的效率变化，scalei为城市常住人口规模，X为影响城市效率变化的其他因素，μi为扰动项。为了检验城市效率变化和城市规模的关系，不预设其函数关系，而将其设定为g（scalei），将其他影响城市效率变化的已知函数关系的变量设定为线性关系。通过Robinson提出的方法[10]，分步估计出线性部分和非参数部分，其中非参数部分为逐点估计值，这样便可以根据逐点的估计值绘出城市效率变化与城市规模之间的关系图。

城市效率变化对城市规模的半参数估计结果中，回归中线性部分的系数和显著性水平与参数回归结果并无太大变化文中并未列出半参数回归参数部分的结果，读者可向作者索取。 ，绘出城市效率变化的估计结果和城市规模的关系（图3）。结果显示，城市效率变化和城市规模也是近似U型曲线关系，曲线最低点位于城市规模为450万人左右，与参数估计结果的544万人相近。Hardle等[11]提出的设定检验P值为035，不能拒绝半参数估计结果可以用二项式参数回归替代，说明前面对城市规模的模型函数形式设定是正确的，城市效率变化和城市规模之间U型曲线关系的结果是稳健的。

图3城市效率变化与城市规模半参数估计结果

注：图中深色曲线为非参数估计的城市效率变化与城市规模的拟合线，深色曲线上下的两条浅色曲线表示95%置性区间4结论与政策建议

本文用DEAMalmquist方法计算了2000年和2010年中国209个地级市市辖区的城市效率，用非参数方法估计了城市效率在不同规模城市间的分布，并实证了城市效率变化及其影响因素。研究发现，我国城市效率和城市规模总体呈现正相关关系，但不同时期我国城市效率分布会发生变化，2000年到2010年，我国城市最优规模均值从350万人增加至717万人，增长了10486%，而同期我国城市规模增长平均只有5047%，我国城市集聚不足的情况在继续加剧，造成城市效率整体下降。对城市效率变化的实证结果显示，城市效率变化和城市规模呈现U型曲线关系，处于544万左右的城市效率降低最快，城市基础设施对提升城市效率有显著影响。

同时，我国的城市政策应加快城市化进程，改善城市基础设施，促进产业转移，推动城市集聚，提高城市效率。特大城市、大城市和中小城市集聚不足，效率提升潜力巨大，地方政府应加大基础设施建设投资，改善城市基础设施以吸引产业和人口集聚，促进中小城市的集聚。部分巨大城市存在规模偏大，应适当限制城市规模，加快产业向集聚不足的城市转移，防止城市“摊大饼”式发展。

参考文献：

[1]王小鲁，夏小林.优化城市规模，推动经济增长[J].经济研究，1999（9）：22-29.

[2]Au C，Henderson V.Are Chinese Cities Too Small[J].The Review of Economic Studies，2006（3）：549-576.

[3]李 郇，徐现祥，陈浩辉.20世纪90年代中国城市效率的时空变化[J].地理学报，2005（7）：615-625.

[4]李红锦，李胜会.基于DEA模型的城市群效率研究——珠三角城市群的实证研究[J].软科学，2011（5）：91-95.

[5]邵 军，徐康宁.我国城市的生产率增长、效率改进与技术进步[J].数量经济技术经济研究，2010（1）：58-66.

[6]Charnes A，Cooper W，Rhodes E.Measuring the Efficiency of Decision Making Units[J].European Journal of Operational Research，1978（2）：429-444.

[7]Banker D，Charnes A，Cooper W.Some Models for Estimating Technical and Scale Inefficiencies in Data Envelopment Analysis[J].Management Science，1984（9）：1078-1092.

[8]张 军，吴桂英，张吉鹏.中国省际物质资本存量估算：1952～2000[J].经济研究，2004（10）：35-44.

[9]Glaeser L，Scheinkman A，Shleifer A.Economic Growth in A CrossSection of Cities[J].Journal of Monetary Economics，1995（1）：117-143.

[10]Robinson M.RootNConsistent Semiparametric Regression[J].Econometrica，1988（4）：931-954.

[11]Hardle W，Mammen E.Comparing Nonparametric Versus Parametric Regression Fits[J].The Annals of Statistics，1993（4）：1926-1947.

（责任编辑：王惠萍）