期望在不确定性风险决策中的应用

袁爽

摘 要：期望是反映随机变量总体取值的平均水平的一个重要的数字特征。经济生活中， 有许多问题都可以直接或间接的利用期望理论来解决。本文通过案例分析不确定性风险决策中的期望值法以及与其他决策的基本方法之间的比较，学习和掌握如何处理风险决策问题。

关键词：期望；不确定性风险；决策

一、期望效用与决策分析

1.期望效用在决策论中的理论与方法。期望效用理论决策问题的因素包括：行动集A，状态集S，后果集X。

Bernoulli原理：一个人面临着必须从已知行动集A中做出选择的决策问题，其中给定的行动后果由未来自然状态S确定，并且未来状态出现的概率P（S） 已知或可估测，则他必然选择一个将产生最高期望值的行动。

该原理的假定：在后果集X上存在一个数值函数∪ ，可用来表示决策者的偏好结构。这个函数便是效用函数，用数学式子表示如下：当自然状态S是离散值时，最优决策方案

期望效用在不确定性风险决策中常用的方法是以期望值为标准的决策方法。

2.现实案例分析。例题：某市一家报社，长期以来每天印制报纸15万份供发行。过去报社一直未注意经济核算。亏损由国家补贴。近来各行业实行经济承包责任制，报社领导要求增加盈利。经查阅100天的报纸销售情况：12天销售15万份，20天销售14万份，30天销售约13万份，25天销售约约12万份，13天销售约11万份。报纸每份售价为5分，成本为4分。所以领导认为改善经营的关键是改印刷的惯例。应当根据市场销售情况确定一个最恰当的印刷数目使所获利润为最大值。为此，他们利用决策分析方法帮助自己解决这个风险性决策问题。备选方案共有五个：设 Al-印刷发行11万份，A2-印刷发行12万份。A3-印刷发行13万份，A4-印刷发行14万份，A5-印刷发行15万份。

3.最大期望收益值决策法.自然状态共有五种：方案A1：概率为 P1 =0.13（ 1 3 天 1 0 0 天 P2= 0.1 3，方案A2：概率为P3 = 0.25，方案A3：概率为P3= 0.30，方案A 4：概率为P4= 0.20，方案A5：概率为 P5= 0.12

根据期望收益值的公式得出：方案A1-A5期望收益值分别为110 0元、1135元、1045元、805元、465元。可看出，方案A2的期望收益值最大，为最佳方案。

4.最小期望损失值决策法

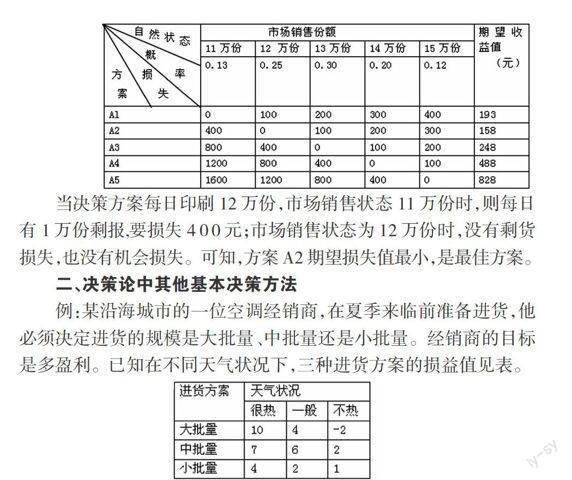
编制决策损失表如下：

当决策方案每日印刷12万份，市场销售状态11万份时，则每日有1万份剩报，要损失4 0 0 元；市场销售状态为12万份时，没有剩货损失，也没有机会损失。可知，方案A2期望损失值最小，是最佳方案。

二、决策论中其他基本决策方法

例：某沿海城市的一位空调经销商，在夏季来临前准备进货，他必须决定进货的规模是大批量、中批量还是小批量。经销商的目标是多盈利。已知在不同天气状况下，三种进货方案的损益值见表。

1.乐观决策分析法。解：大批量max （10，4，-2）=10（万元），中批量max（7，6，2）=7（万元），小批量max（4，2，1）=4（萬元）；max（10，7，4）=10（万元），根据乐观准则，选择大批量进货为最优决策方案。

2.悲观决策分析法。解：批量min （10，4，-2）=-2（万元），中批量min（7，6，2）=2（万元），小批量min（4，2，1）=1（万元）；max（-2，2，1）=2（万元），根据悲观决策法，选中批量进货为最优方案。

3.折中的决策分析法。根据实际情况和自己的实践经验确定一个乐观系数（0<