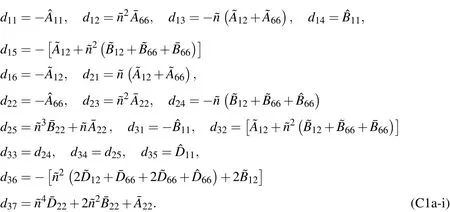Three-Dimensional Free Vibration Analysis of Sandwich FGM Cylinders with Combinations of Simply-Supported and Clamped Edges and Using the Multiple Time Scale and Meshless Methods
2015-04-20ChihPingWuandRueiYongJiang
Chih-Ping Wuand Ruei-Yong Jiang
1 Introduction
The exact and approximate three-dimensional(3D)analysis of functionally graded material(FGM)plates/shells has attracted considerable attention in the last decade due to the fact that the material properties of FGM plates/shells continuously and gradually vary through their thickness,which may overcome some drawbacks of conventional laminated composite plates/shells,such as delamination,thermal stress concentration,and matrix cracking.The related 3D solutions may provide a reference for assessing the two-dimensional(2D)theoretical methodologies and numerical models.Among these,however,relatively few articles consider the 3D analysis of plates/shells with various boundary conditions compared to those that examine plates/shells with fully simply-supported edges.A comprehensive literature survey with regard to various 3D coupled piezo-thermo-mechanical analyses of FGM plates/shells has been carried out by Wu et al.(2008),and the relevant re fi ned and advanced 2D analyses of these have also been reviewed[Carrera(2000,2003);Carrera and Birschetto(2009);Carrera and Ciuffreda(2005);Carrera et al.(2008);Cinefra et al.(2010);Carrera et al.(2010);Liew et al.(2015);Saravanos and Heyliger(1999);Swaminathan et al.(2015)].
Wu et al.(2008)classi fi ed the analytical methods used for the 3D analysis of simply-supported,multilayered FGM structures and laminated composite ones into four different approaches,namely the state space[Chen and Ding(2002);Wu and Liu(2007);Zhong and Yu(2006);Zhang et al.(2014)],Pagano[Heyliger and Brooks(1995,1996);Wu and Tsai(2012)],series expansion[Dube et al.(1996a,1996b);Dumir et al.(1997)]and perturbation[Wu et al.(1996a,1996b);Wu and Tsai(2010)]methods.In addition,Brischetto(2013)presented the exact 3D solutions for the free vibration of FGM plates and shells.The formulation was developed in the general orthogonal curvilinear coordinates,and the exponential matrix method was used to solve the system equations.In the first three approaches,the analytical solutions of which can be obtained only for the system of constant coefficient equations,a successive approximation(SA)method[Soldatos and Hadjigeorgiou(1990)]is used for FGM plates/shells with variable-coefficient equations.In the SA method,FGM plates/shells are artificially divided into a series of homogeneous layers with an equal and small thickness for each layer,and their effective material properties are estimated in an average sense,such that the multilayered homogeneous structures can be used to approximately model the FGM ones when the number of individual layers becomes greater.Unlike the above mentioned methods,the interlaminar field variables in the perturbation method are derived as a de finite integration through the thickness coordinate,and can be directly determined without using the SA method,and the perturbation method may thus be better in this context than the other three approaches.
In the decade,the meshless method has been used as an alternative approach to the finite element method(FEM)in computational mechanics.Unlike FEM[Wu and Li(2010,2013);Xie and Chi(2014)],for which the development of the interpolation functions of unknown variables relies strongly on an assigned grid mesh,those in the meshless methods are entirely constructed in terms of random distributions of nodes using the differential reproducing kernel(DRK)method[Chen et al.(2011);Wang et al.(2010)],the moving least square method[Sladek et al.(2003,2006,2010)]and radial basis functions[Ferreira et al.(2003);Roque et al.(2005)].A comprehensive literature survey of meshless methods has been undertaken[Belytschko et al.(1996);Atluri and Shen(2002);Li and Liu(2004);Liew et al.(2011)].Among these,a truly meshless method,the meshless local Petrov-Galerkin(MLPG)method,was developed by Atluri and Zhu(1998),in which no assigned meshes were required for constructing the interpolation functions of the field variables and for the integration evaluations of the stiffness,mass and geometric stiffness matrices.The MLPG method has been extended to various mechanical analyses of elastic solids and structures,such as thermal shock[Hosseini et al.(2011)],wave propagation[Moussavinezhad et al.(2013)],transient elastodynamic[Sladek et al.(2007)],thermal bending[Sladek et al.(2008)]analyses.Finally,a review of applications of the MLPG method in engineering and sciences was undertaken by Sladek et al.(2013).
To the best of the authors’knowledge,the perturbation method and multiple time scales ones have been sucessfully applied to the 3D static and dynamic analyses,respectively,of simply-supported,FGM plates/shells[Wu and Syu(2007);Wu and Tsai(2009)]in the open literature,while these can not be directly applied to the structures with various boundary conditions.An asymptotic DRK-based meshless method is thus developed in this work for the 3D free vibration analysis of sandwich FGM circular hollow cylinders with combinations of simply-supported and clamped edges,in which the multiple time scales method[Nayfeh(1981)]is replaced by the regular perturbation method.Using direct elimination,we first reduce the fifteen partially differential equations(PDEs)of the 3D elasticity theory to six PDEs in terms of six primary variables of elastic fields,which are three displacement components and three transverse shear and normal stress ones.Through the mathematical manipulation of nondimensionalization,asymptotic expansion and successive integration,we finally obtain recurrent sets of motion equations for various order problems.Classical shell theory(CST)is derived as a first-order approximation of the 3D elasticity theory,and the motion equations for higher-order problems retain the same differential operators as those of CST,although with different nonhomogeneous terms.These features will be very less time-consuming,because the solution process of the leading order can be repeatedly used by meansof recalculating the corresponding nonhomogeneous terms only.Expanding the primary field variables of each order as the Fourier series functions in the circumferential direction,and interpolating these in the axial direction using the DRK interpolation,we can obtain the leading-order solutions of this analysis,and the higher-order modifications can then be determined in a systematic and consistent manner,in which the solvability and normality conditions are used to eliminate the secular terms and uniquely determine the modal variables when we apply the solution process to the first-order problems,and then to much higher-order ones.Some benchmark solutions for the dynamic responses of simply-supported,sandwich FGM circular hollow cylinders and laminated composite ones are given to demonstrate the performance of the asymptotic DRK-based meshless method,and the results for the cylinders with combinations of simply-supported and clamped boundary conditions may provide a standard for assessing those obtained using the 2D analytical and numerical methods.Moreover,the effects of the materialproperty gradient index,and different aspect ratios and boundary conditions on the natural frequencies of the cylinders and their corresponding through-thickness distributions of interlaminar modal variables,and the deviations between the results obtained using the rules of mixtures and the Mori-Tanaka scheme are also examined.
2 Basic equations of 3D elasticity
As shown in Fig.1,we consider a functionally graded elastic circular hollow cylinder,of which the thickness is 2h.A set of cylindrical coordinates(x,θandr)is located at the center of the cylinder,and the thickness coordinate(ζ)is measured from the mid-surface of this.RandLdenote the radius and length of the cylinder,and the relation between the radial coordinate(r)and the thickness one(ζ)isζ=r−R.
The linear constitutive equations valid for the symmetrical class of elastic materials are given by
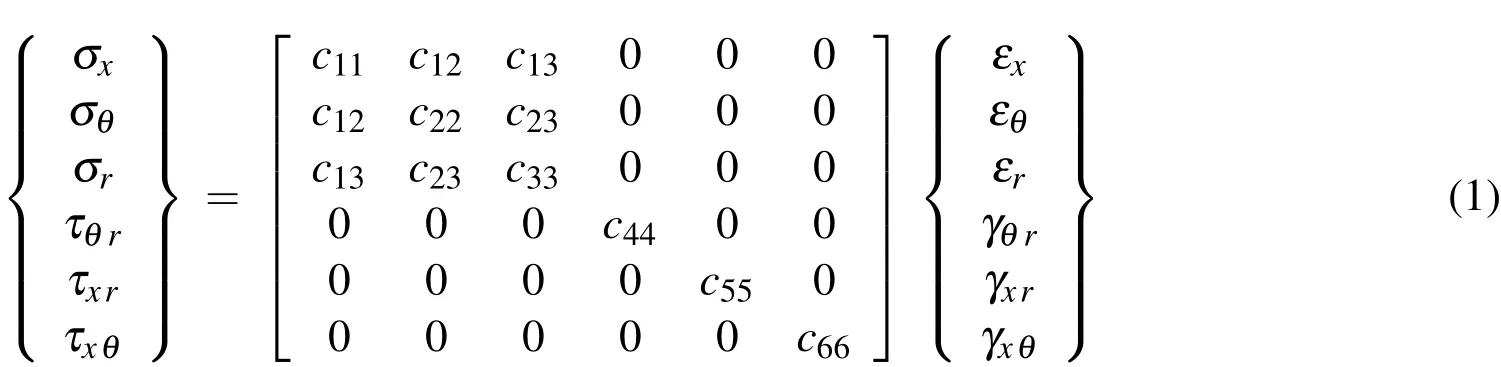

Figure 1: The configuration and coordinates of a sandwich circular hollow cylinder with either FGM face sheets or an embedded FGM core.
The strain-displacement relations in the cylindrical coordinatesx,θ,andrare given by
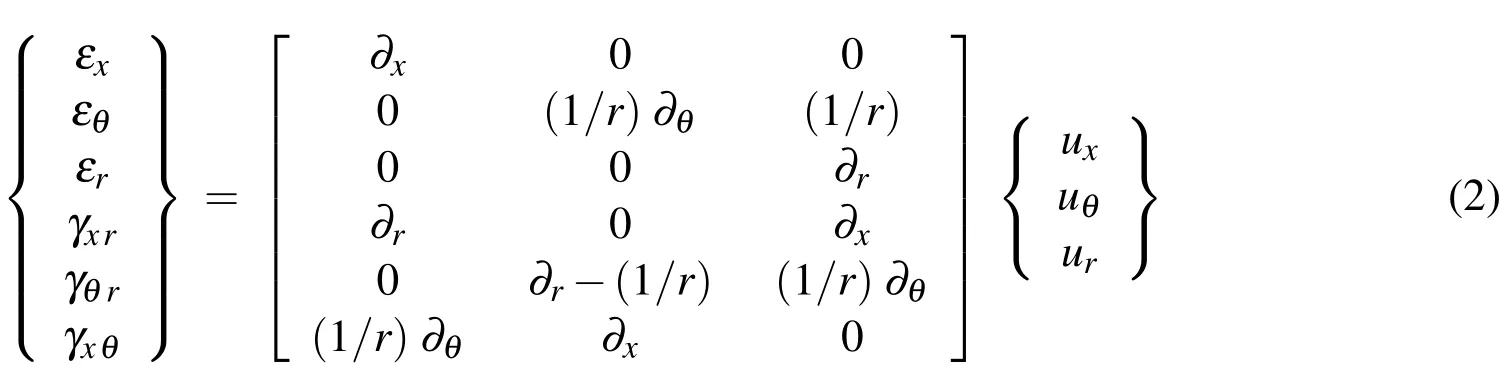
in whichux,uθandurare the displacement components,and∂k=∂/∂k(k=x,θandr).
The stress equilibrium equations of an elastic body without accounting for body forces are given by
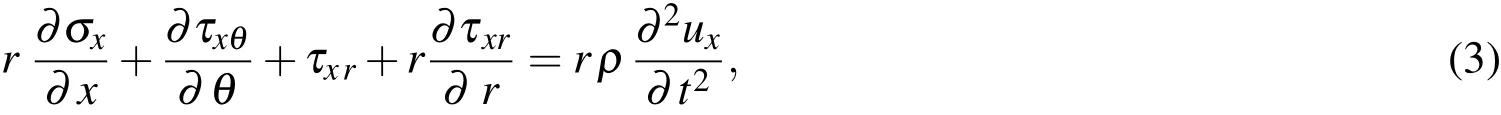

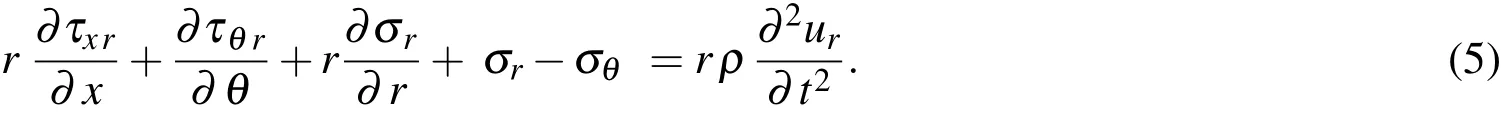
in whichρdenotes the mass density of the elastic body considered,andtis the time variable.
The boundary conditions for the free vibration problem of the FGM cylinder are specified,as follows:
On the lateral surface the transverse loads are given by

The edge boundary conditions of the cylinder are considered as either simply supported or clamped ones,and are given,as follows:
For the simply-supported edge,

For the clamped edge,

3 Nondimensionalization
A set of dimensionless coordinates and elastic field variables is defined,as follows:

where∈2=h/R,andQdenotes a reference elastic modulus,the value of which is taken to be the same as the Young’s modulus inxdirection(E11)at the bottom of the cylinder in this article.The dimensionless multiple time scales are defined,as follows:
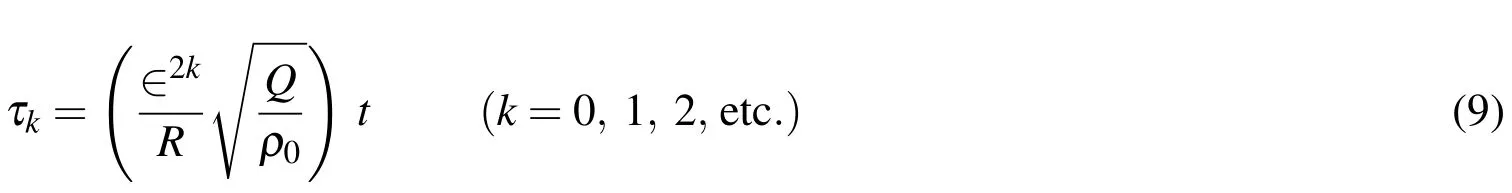
in whichρ0denotes a reference mass density,and is taken to be the same as that at the bottom of the cylinder in this article.
As shown in Eqs.(1)_(5),there are fifteen basic equations of 3D elasticity theory for the free vibration analysis of FG elastic circular hollow cylinders.In order to make the previous complicated formulation suitable for mathematical treatment,we eliminate the in-surface stressand straincomponents from Eqs.(1)-(5),introduce Eqs.(8)and(9)in the resulting equations,and then express the 3D basic equations in terms of the dimensionless forms of displacementand transverse stresscomponents,as follows:
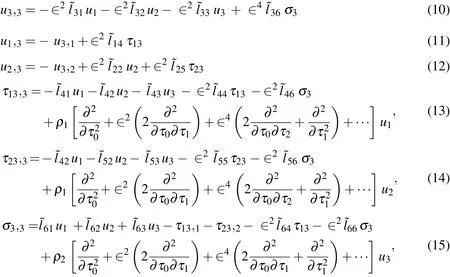
where
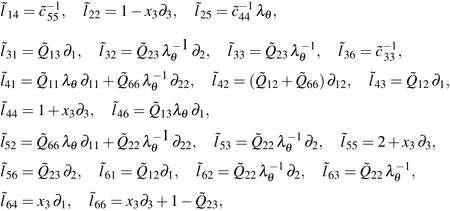
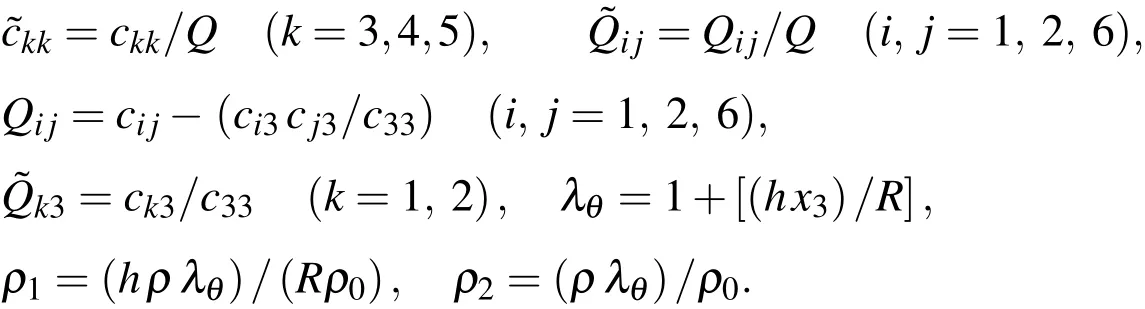
Following a similar derivation process,we rewrite the in-surface stresses in the dimensionless form as

where
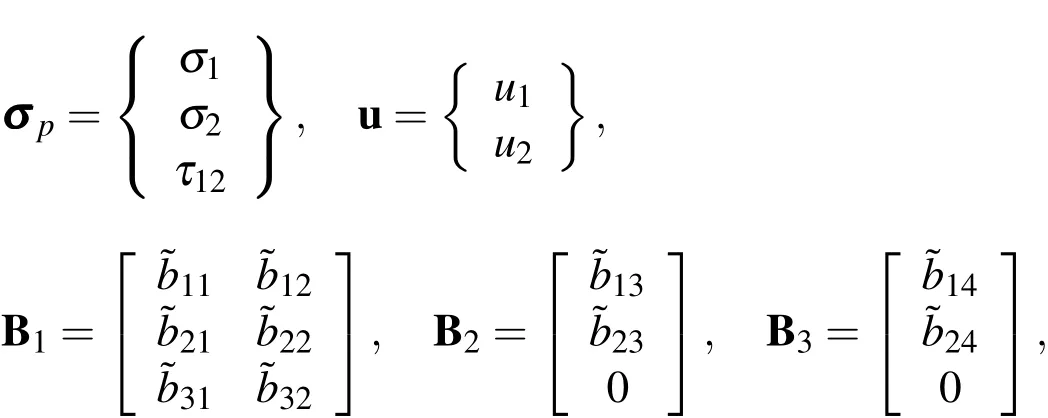
and
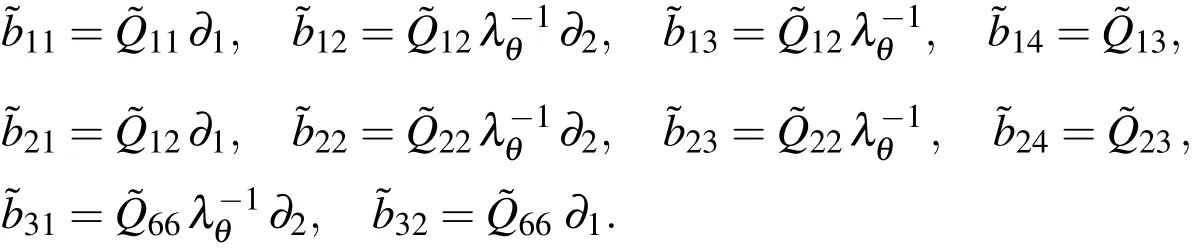
The dimensionless forms of the boundary conditions of the problem are specified,as follows:
On the lateral surface,the transverse loads are given by
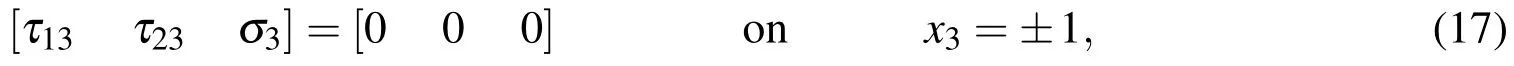
For the simply-supported edge,

For the clamped edge,

4 Asymptotic expansion
By observation of Eqs.(10)-(16),we fi nd that these contain terms involving only even powers of∈.We thus asymptotically expand the field variables in the powers∈2,as given by
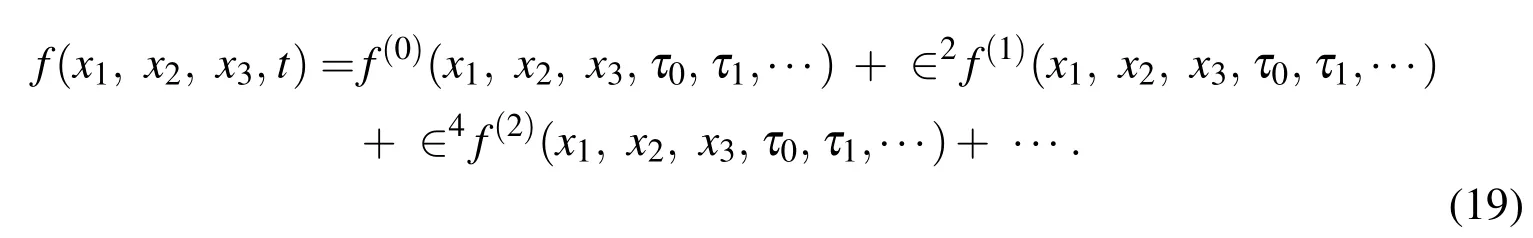
Substituting Eq.(19)into Eqs.(10)-(16)and collecting coefficients of equal powers of∈,we obtain the following sets of recurrence equations.
Order∈0:

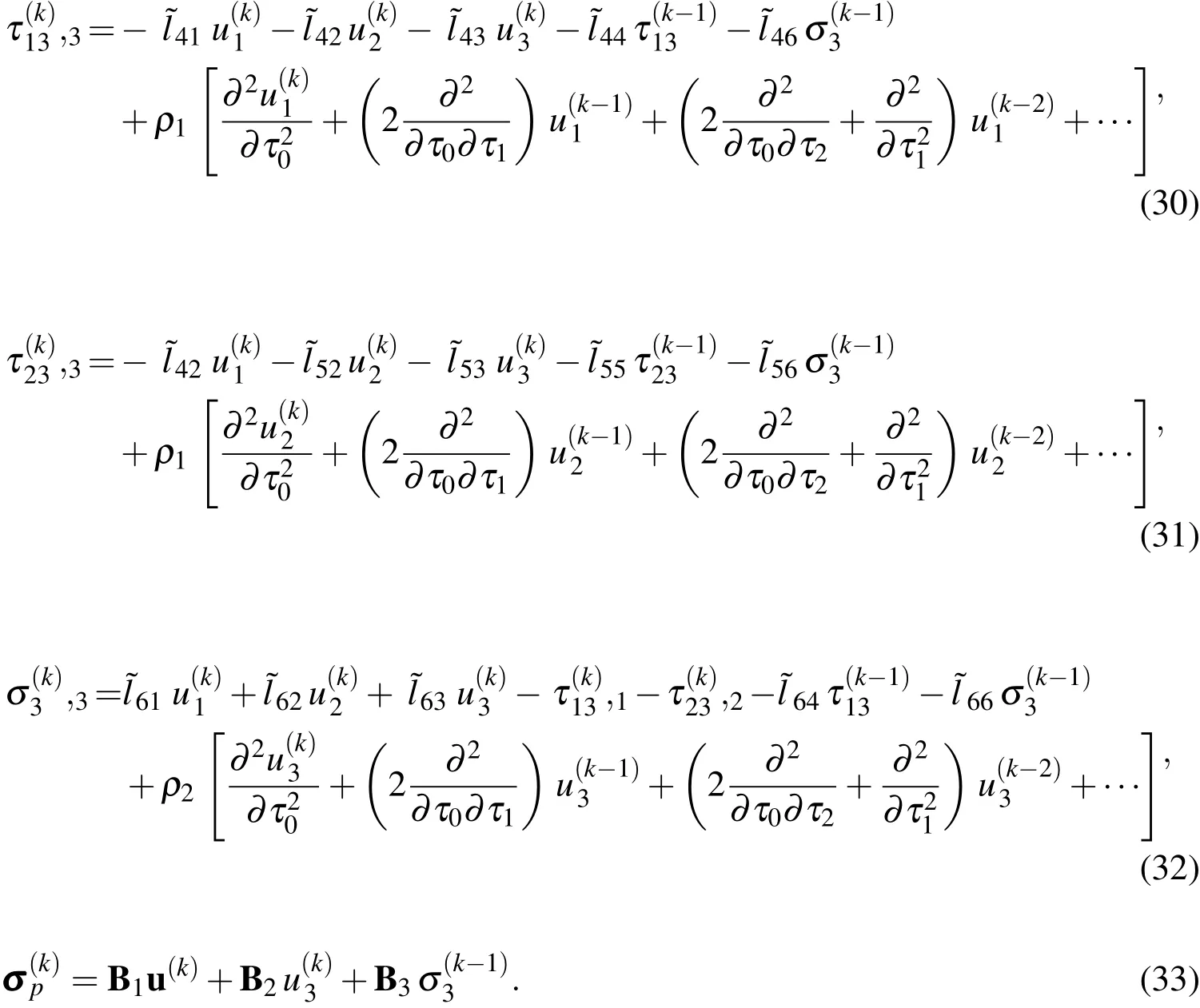
The boundary conditions for various order problems are specified,as follows:
On the lateral surface the transverse loads are given by
Order∈2k(k=0,1,2,3,etc),

For the simply-supported edge and order∈2k(k=0,1,2,3,etc),

For the clamped edge and orderε2k(k=0,1,2,3,etc),

5 Asymptotic integration and various order problems
5.1 The leading-order problem
We examine the sets of asymptotic equations and fi nd that the present analysis can be carried out by integrating these through the thickness direction.We thus integrate Eqs.(20)-(22)to obtain
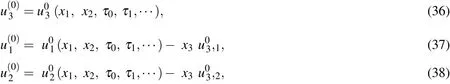
With the lateral boundary conditions onx3=-1 given in Eq.(34),we then proceed to integrate Eqs.(23)-(25),which yields
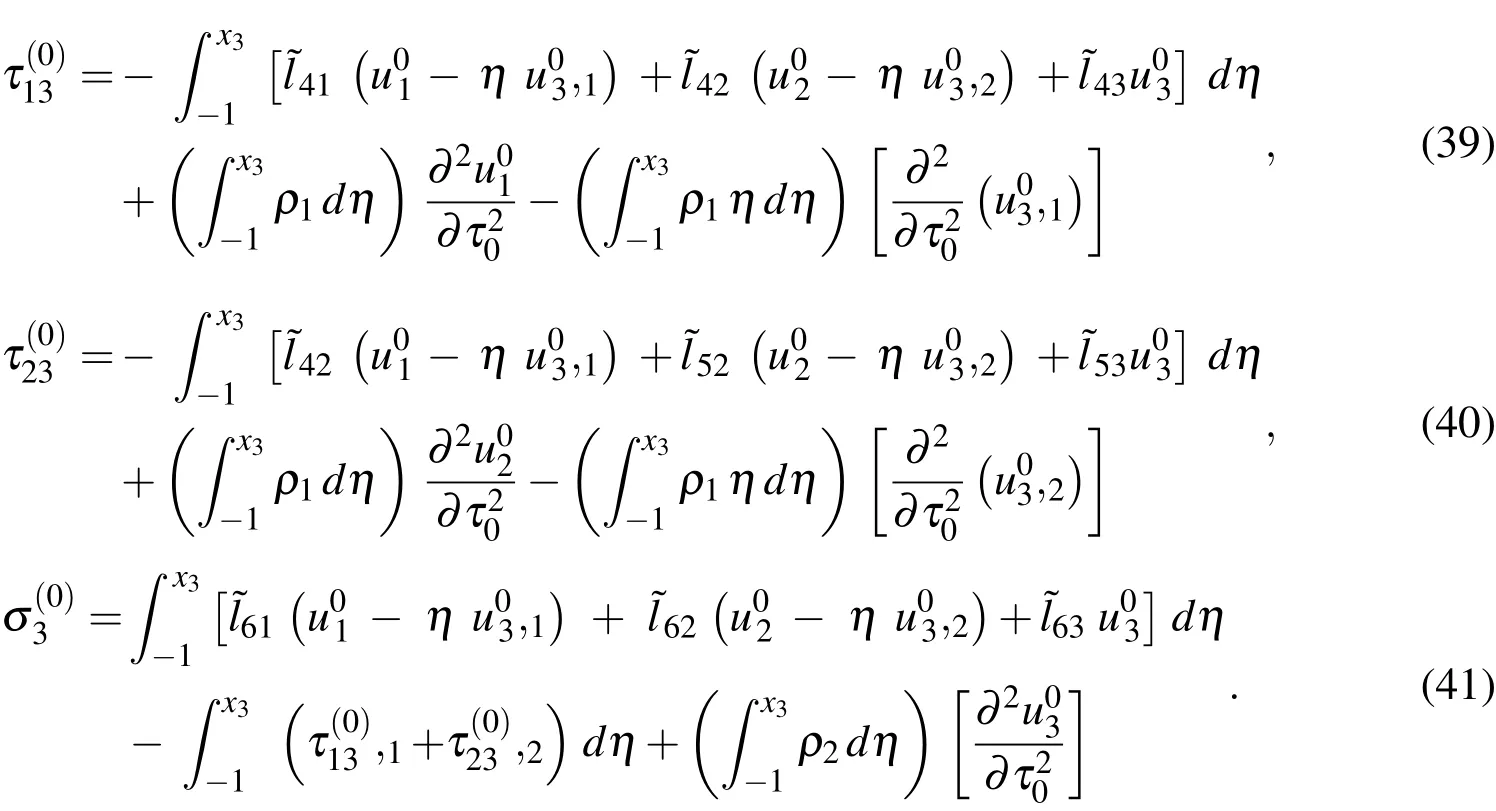
Imposing the remaining lateral boundary conditions onx3=1 given in Eq.(34)in Eqs.(39)-(41),and reorganizing the resulting equations,we finally obtain the motion equations for the leading(∈0)order,as follows:
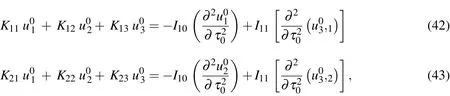
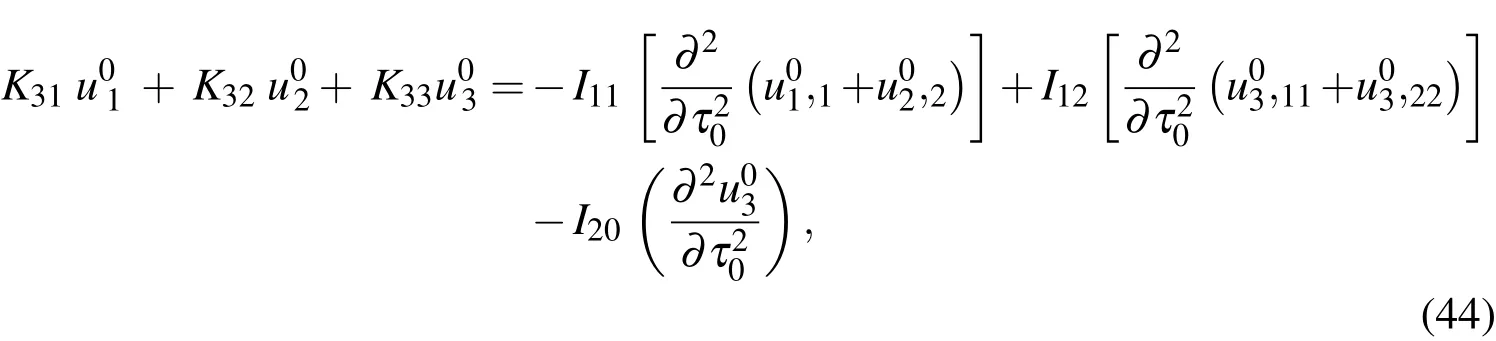
whereKij(i,j=1-3)andIkl(k=1,2;l=0-2)are the relevant differential operators,and these are given in Appendix A.
In this article,the edge boundary conditions of the cylinder are considered as combinations of the simply-supported and clamped edges.After the asymptotic process,we thus obtain the edge conditions for the leading-order problem,as follows:Case 1.For simple-simple(SS)supports,
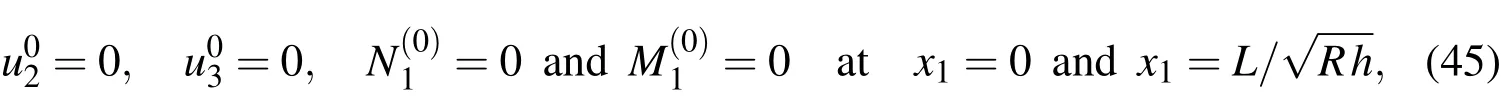

Case 2.For simple-clamped(SC)supports,
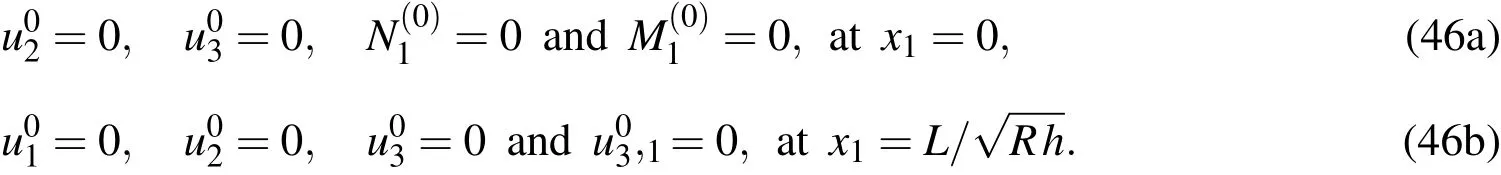
Case 3.For clamped-clamped(CC)supports,
It is noted that the CST governing equations are recovered from Eqs.(42)-(44)by introducing a geometric assumption with regard to the thin shell:x3/R<<1.CST has thus been derived as a first-order approximation of the 3D theory.Solutions of Eqs.(42)-(44)must be supplemented with one of the appropriate edge boundary conditions given in Eqs.(45)-(47)to constitute a well-posed boundary value problem.Once the variables ofu01,u02andu03are determined,the leadingorder solutions of modal displacements are given by Eqs.(36)-(38),the modal transverse shear and normal stresses by Eqs.(39)-(41)and the modal in-surface stresses by Eq.(26).
为实现对车辆的精确管理,从车辆运行到车辆停放进行多维度的全面信息采集,并从交通管理、交通治安的角度进行考虑,设置多级卡口实现车辆的多维度监管.
5.2 Higher-order problems
Proceeding to order∈2kand following the same process as before, we readily obtain

where
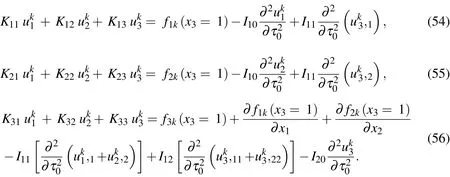
The edge conditions for the higher-order problems are given,as follows:
Case 1.For simple-simple(SS)supports,
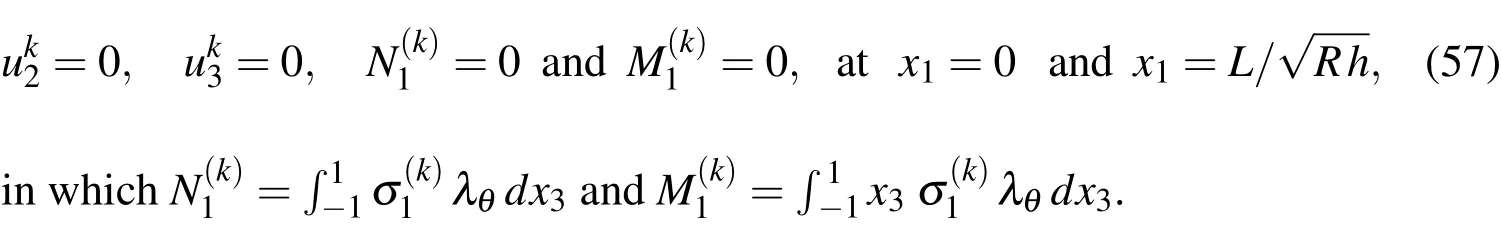
Case 2.For simple-clamped(SC)supports,
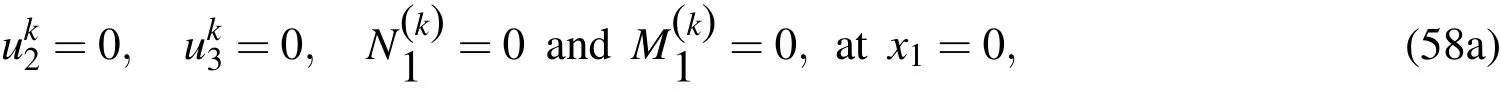
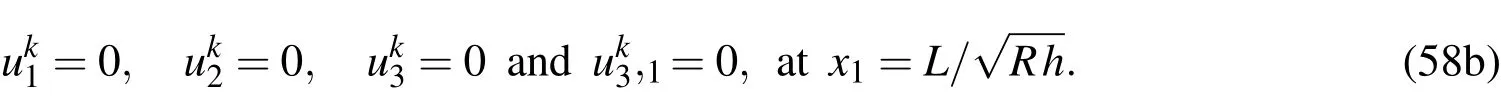
Case 3.For clamped-clamped(CC)supports,

The higher-order modifications of mid-surface displacement componentscan be obtained by solving Eqs.(54)-(56)combined with one of the appropriate edge conditions given in Eqs.(57)-(59),and once these are determined,the higher-order modifications of displacement components are given by Eqs.(48)-(50),the transverse shear and normal stresses by Eqs.(51)-(53)and the in-surface stresses by Eq.(33).
By observation of the governing equations of the leading-order problem(Eqs.(42)-(44))and the higher-order problems(Eqs.(54)-(56)),we fi nd that the differential operators among the various order problems remain identical,and the nonhomogeneous terms of higher-order problems can be calculated from the lower-order solution.It is thus shown that the solution process of the leading-order problem can be repeatedly applied to the higher-order problems.The present asymptotic solutions can be determined order-by-order in a hierarchical and consistent manner.
6 DRK interpolation
In this article,the DRK interpolation functions[Wang et al.(2010)]are used to construct the shape functions of the primary field variables of this problem in the axial(x1)direction,and the DRK interpolation functions and their relevant derivatives are brie fl y described,as follows.
It is assumed that there arenpdiscrete nodes randomly selected and located atrespectively,in thex1direction,in which a functionF(x1)is interpolated asFa(x1)and defined as
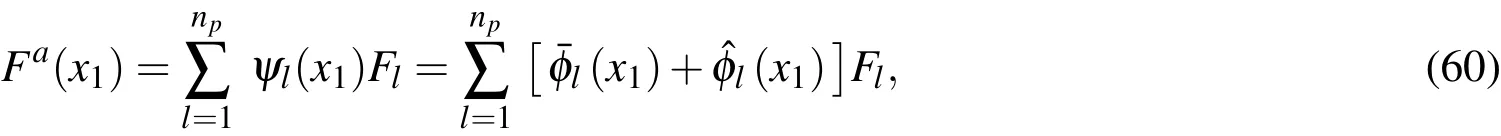
By selecting the completenth-order polynomials as the base functions to be reproduced,we obtain a set of reproducing conditions to determine the undetermined functions ofThese conditions are given as
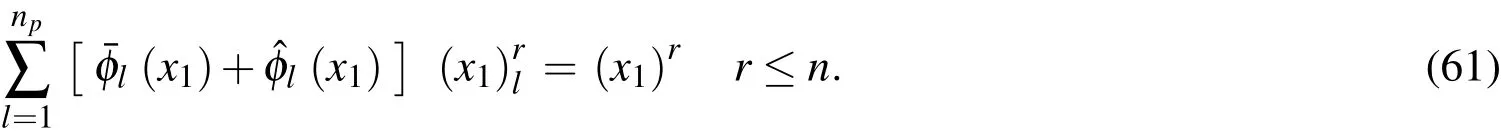
Equation(61)represents(n+1)reproducing conditions,and the matrix form of these is given as

According to these conditions,we may obtain the undetermined function vector(x1)in the following form
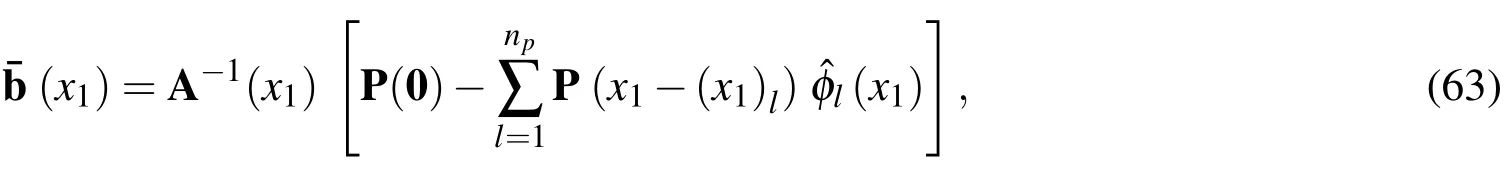
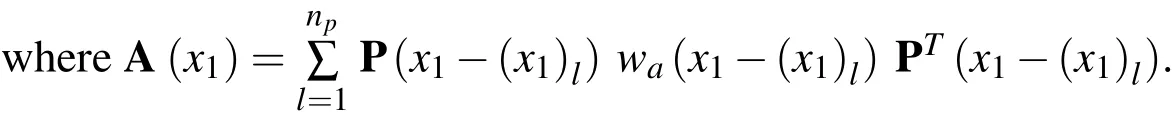
Substituting Eq.(63)into Eq.(60)yields the shape functions ofFa(x1)in the form of
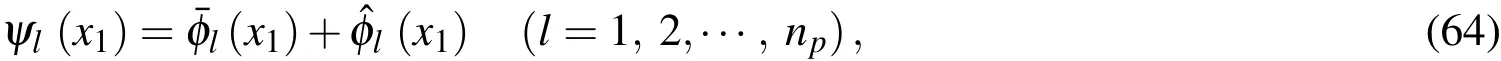
where
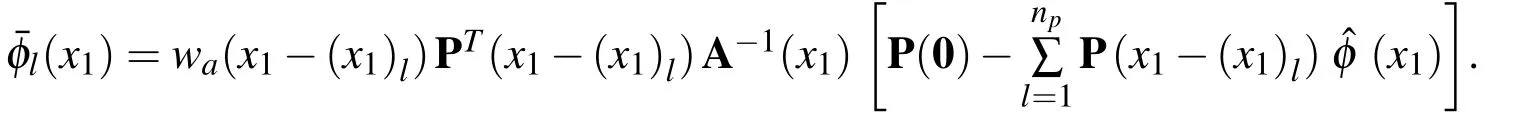
It is noted that if we select a set of primitive functions satisfying the Kronecker delta propertiesa priori,then a set of the shape functions with these properties will be obtaineddue to the fact that the enrichment functions vanish at all the nodes
In implementing the present scheme,the weight and primitive functionsmust be selected in advance.Following Wang et al.(2010),the normalized Gaussian function is selected as the weight and primitive functions at eachsampling node,and this is given as
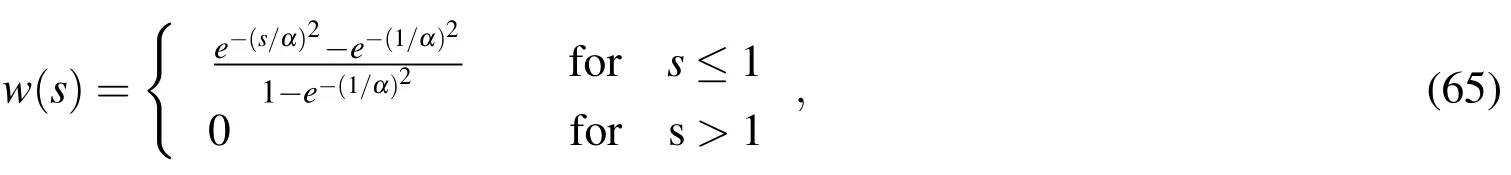
wherewa(x−xl)=w(s),s=|x−xl|/a,andadenotes the radius of the influence zone,which is assigned not to cover any neighboring node for the primitive function,and its optimal value for the weight function will be discussed later in this work.The literature[Wang et al.(2010)]suggestsα=3 for the analysis of an elastic solid,and this is also used in this article.Moreover,the derivatives of these DRK interpolation functions are given in Wang et al.(2010),and not repeated here.
7 Applications
7.1 Leading-order solution
The free vibration problem of sandwich functionally graded elastic circular hollow cylinders and laminated composite ones with simply-supported and clamped edges is studied using the asymptotic DRK-based meshless method,in which the primary variables of displacement and stress components are expanded as the Fourier series functions in the circumferential coordinate,and then the DRK interpolation functions are used to interpolate the variables in the axial coordinate.The motion equations of the leading-order problem can thus be solved by letting
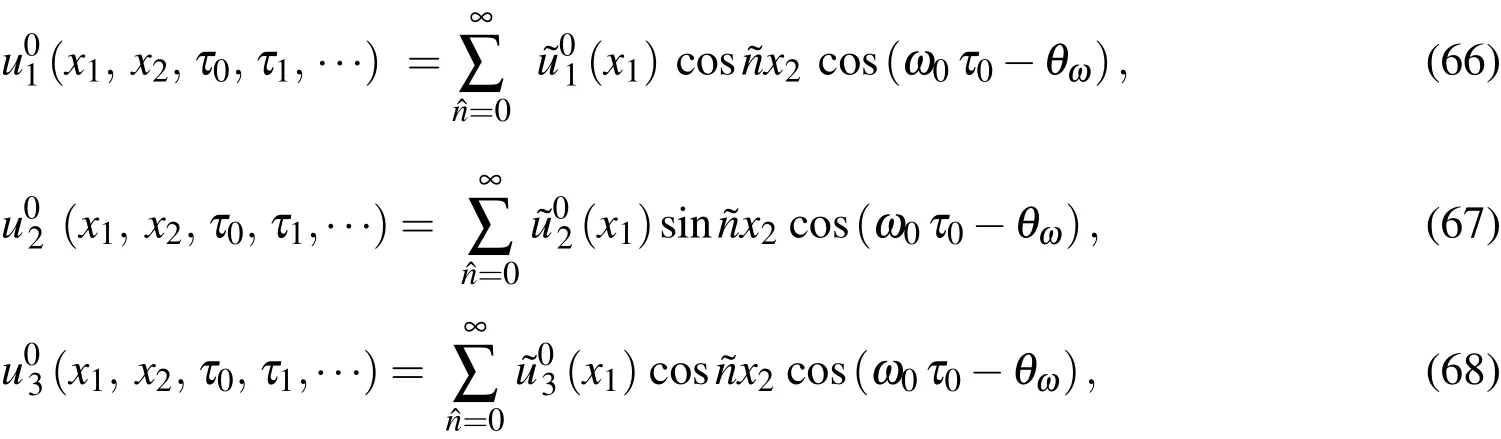
Substituting Eqs.(66)-(68)into Eqs.(42)-(44)gives
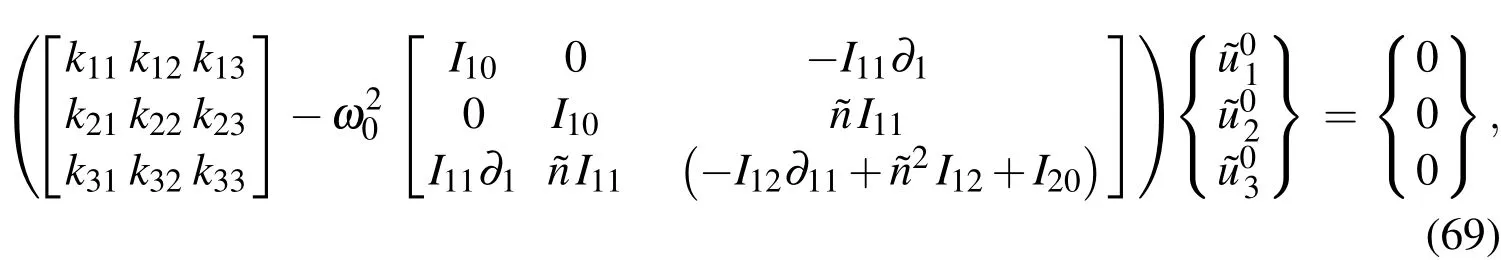
in which the expressions ofkij(i,j=1−3)are given in Appendix B.
Using the DRK interpolation,we express the field variables in the form of Eq.(60)and their higher-order derivatives,and then rewrite the edge boundary conditions and motion equations of the leading order,as follows:
Applying the motion equation(Eq.(69))to the selected sampling node and using the DRK interpolation leads to
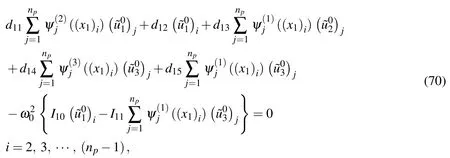

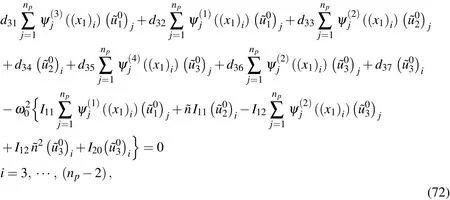
in which the expressions ofdijare given in Appendix C.
Equations(70)-(72)can be rewritten in the matrix form,as follows:
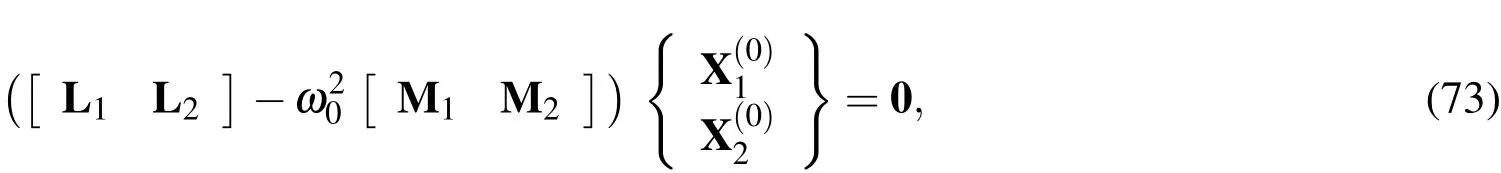
the dimensions of which are(8x1)and[(3np-8)x1],respectively.
Using the DRK interpolation,we rewrite the appropriate edge conditions of Cases 1-3 for the leading order problem,as follows:
Case 1.For the simple-simple(S-S)supports,
Case 2.For the simple-clamped(SC)supports,
Case 3.For the clamped-clamped(CC)supports,
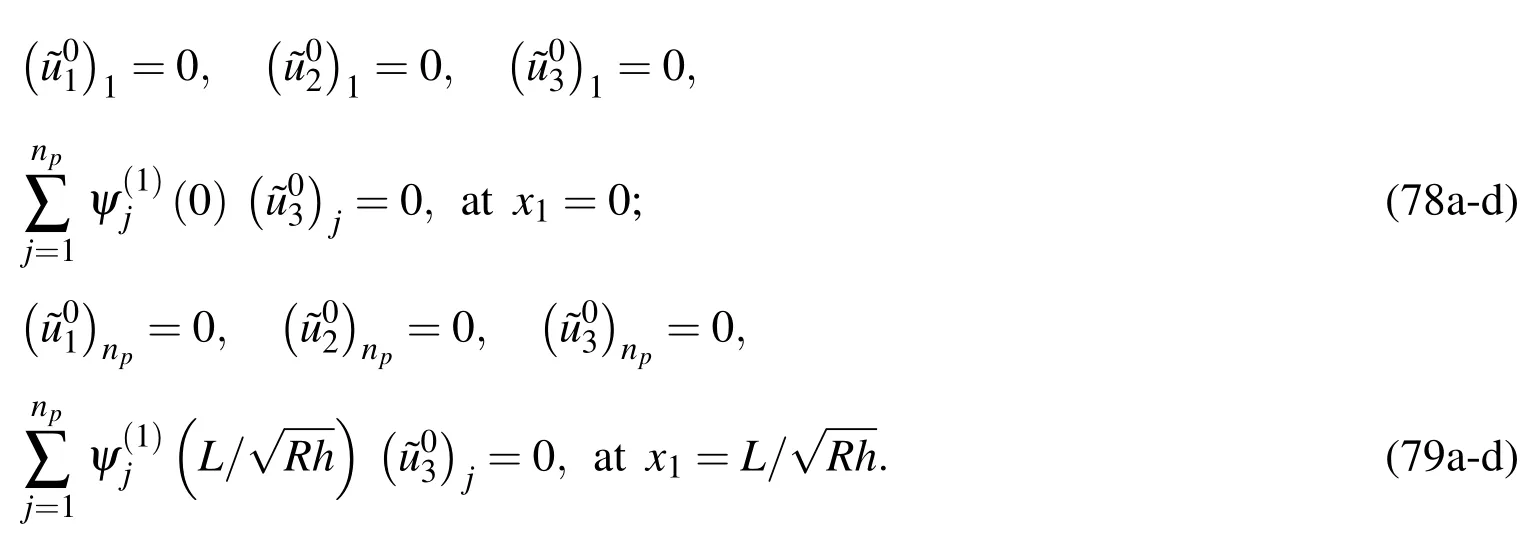
The above boundary conditions can be rewritten in the matrix form,as follows:

The motion equations(70)-(72)associated with one set of the appropriate boundary conditions(Eqs.(73)-(78))represents a standard eigen-valued problem consisting of a set of(3np)simultaneously algebraic equations in terms of 3npunknowns.By satisfying the boundary conditions(80),the motion equations(73)can be rewritten in the form of
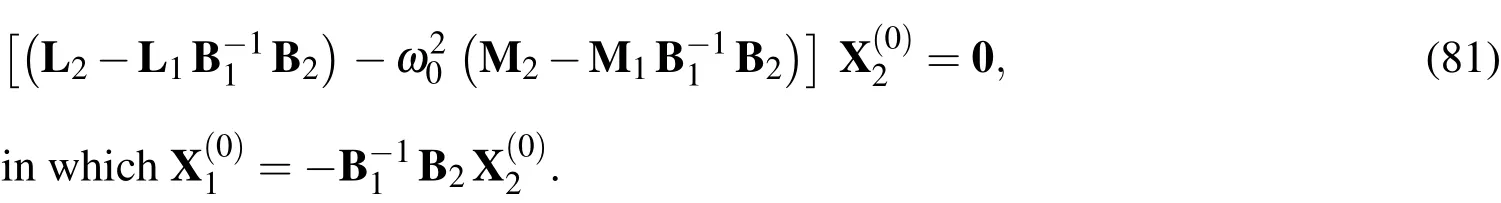
The natural frequencies(ω0)i[i=1−(3np−8)]can then be obtained by letting
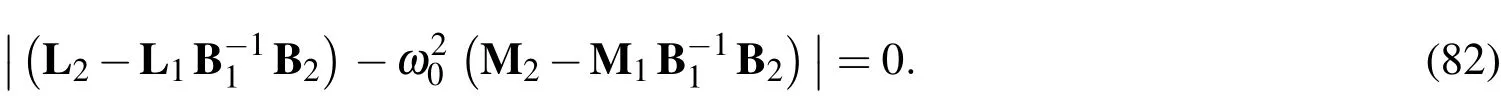
The modal displacement components are normalized to render the asymptotic solution for various orders unique,and these are given by
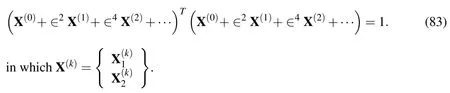
The normality conditions at each level are

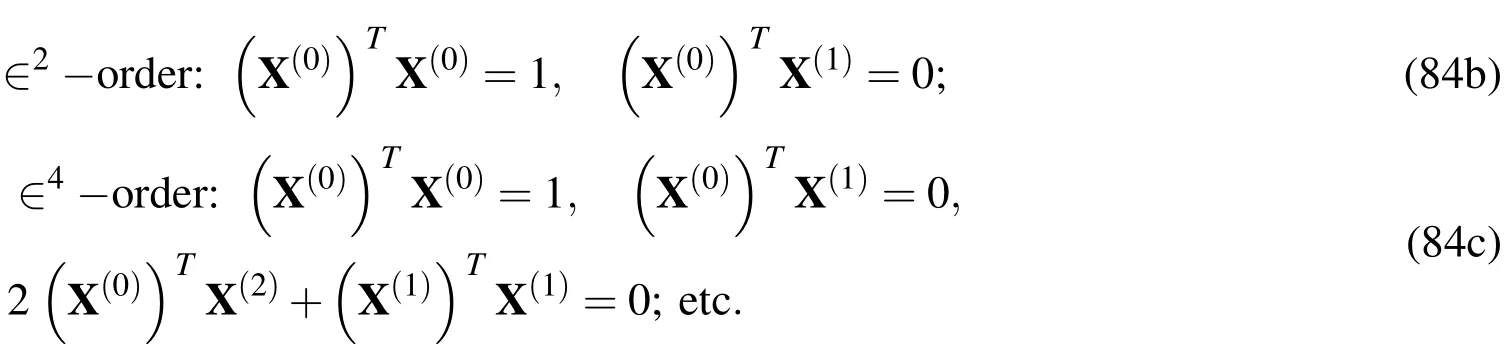
Once the natural frequencies of the leading-order problem((ω0)i)are obtained,the corresponding eigen vectors,which are the modal mid-surface displacement components,can be uniquely determined by using the corresponding normality conditions(Eq.(84a)),and the through-thickness distributions of modal displacement and stress variables for the leading-order problem can thus be determined,as mentioned before.
7.2 First-order modifications
Carrying on the solution to order∈2,we fi ndthatthenonhomogeneous termsi=1−3 and the revelant functionsfor fixed values ofandin the∈2-order equations are
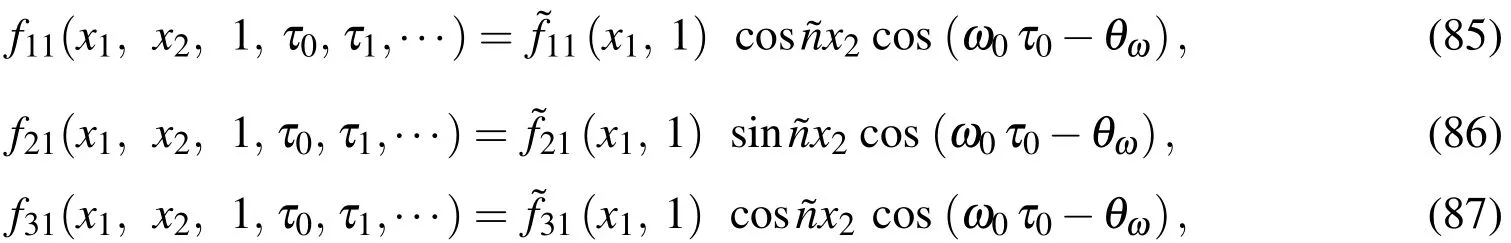
and
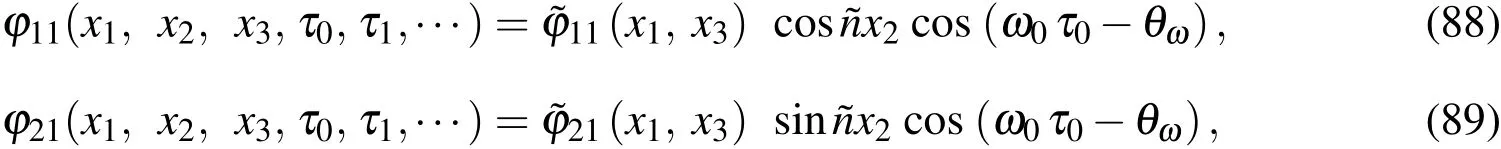
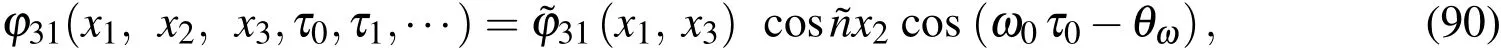
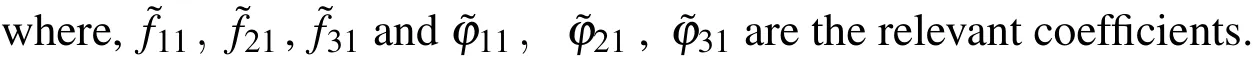
In view of the recurrence of the equations,the∈2-order solution can be obtained by letting
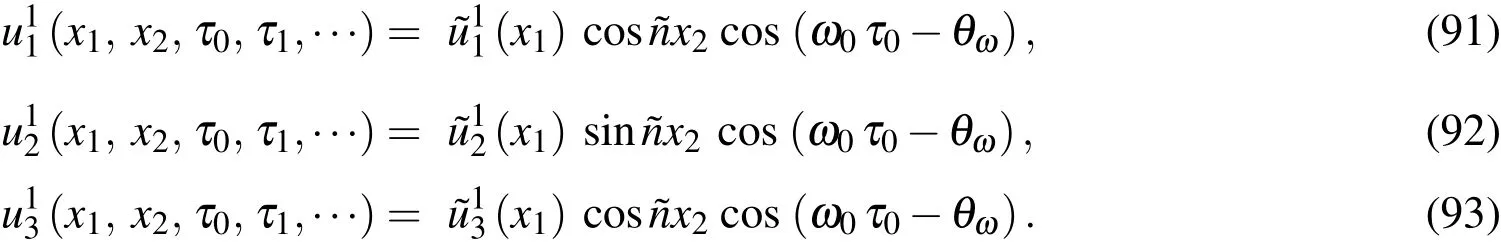
Substituting Eqs.(85)-(93)into Eqs.(54)-(56)gives
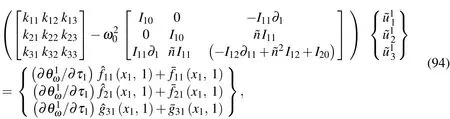

Applying the motion equation(Eq.(94))to the selected sampling node and using the DRK interpolation leads to

The appropriate edge conditions of Cases 1-3 for the∈2-order problem can be written,as follows:

By satisfying the boundary conditions(96),we can rewrite the motion equation(95),as follows:

A solvability condition for a particular vibration mode(i),the natural frequency of which is(ω0)i,is introduced such that Eq.(97)becomes solvable,and this is given by
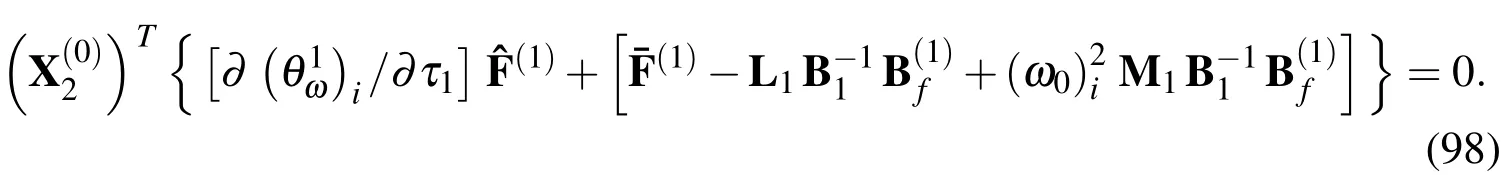
Equation(98)leads to
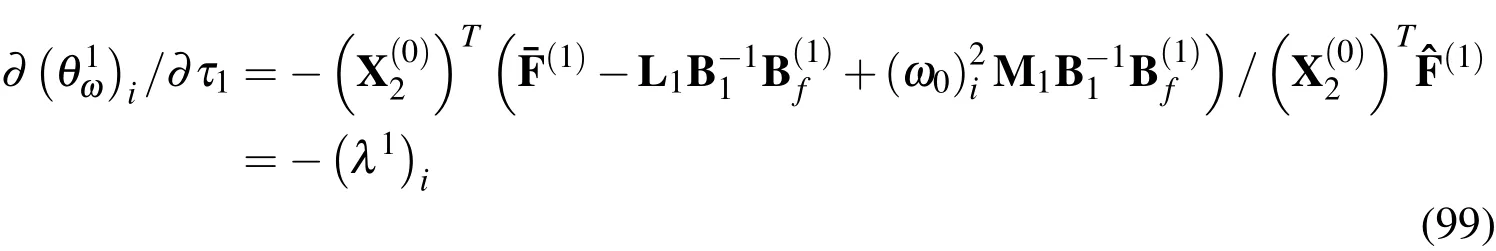
The hamonic time function can then be modified as
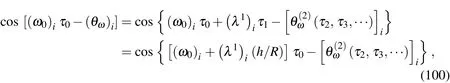
and the natural frequencies for the first-order problem are thus obtained as

By using the solvability conditions(98)and the normality conditions(84b),we can uniquely determine the first-order modifications of interlaminar modal displacement and stress components for theithvibration mode.Moreover,the solution process can be repeatedly applied to higher-order problems(∈2k-order,k=2,3,etc)in a systematic and consistent manner due to the similarity between the system equations of the first-order problem(k=1)and those of much higher-order ones(k=2,3,etc.).
8 Illustrative examples
8.1 Sandwich cylinders with two FGM face sheets
The free vibration problem of simply supported,sandwich FGM cylinders consisting of two FGM face-sheets and a homogeneous core(i.e.,[FGM/core/FGM])asshown in Figs.1(a)and 1(b),which has been studied by Wu and Yang(2011)using the quasi-3D element-free Galerkin method,and Wu et al.(2014)using an exact 3D modified Pagano method,is used to validate the performance of the asymptotic DRK-based meshless method.The thickness for each layer constituting the cylinder ishi(i=1-3),the layer number is counted from the bottom(inner)layer of the cylinder,and the total thickness of the cylinder is 2h,such thath1+h2+h3=2h.The volume fraction of each layer is given as

in whichζ0=−ζ3=−h,ζ1=−ζ2=−h2/2,andκpdenotes the material-property gradient index.
The effective engineering constants and mass density of each layer are evaluated by using the rule of mixtures[Hill(1965)],and are written as follows:
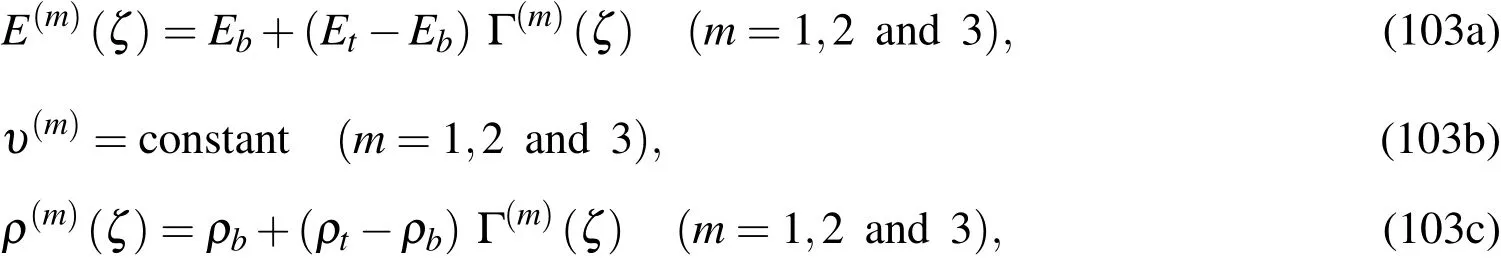
whereEtandEbdenote the Young’s modulus of the top and bottom surfaces of layer 1,which is the bottom layer,andρtandρbare their mass densities.
For comparison purposes,the dimensionless frequency parameter is defined as the same as that used in Wu and Yang(2011)and Wu et al.(2014),which is=The top and bottom surfaces of layer 1(the bottom layer)are considered to be aluminum(t)and alumina(b),respectively,the engineering constants and mass density of which are

Table 1 presents the asymptotic solutions of lowest frequency parameters of sandwich FGM cylinders for different vibration modes with=1−3,in whichL/R=5,R/2h=10,h1:h2:h3=2h/3:2h/3:2h/3,andκp=0,1 and∞.When
κp=0,the sandwich FGM cylinder reduces to a single-layered homogeneous aluminum cylinder,while this reduces to a sandwich homogeneous cylinder(i.e.,[alumina/aluminum/alumina]one)whenκp=∞.
Table 1: The convergence study with regard to the results of lowest frequency parameters of simply-supported,sandwich FGM cylinders for different vibration modes(L/R=5,R/2h=10,h1:h2:h3=2h/3:2h/3:2h/3,=ωR2(2h)).
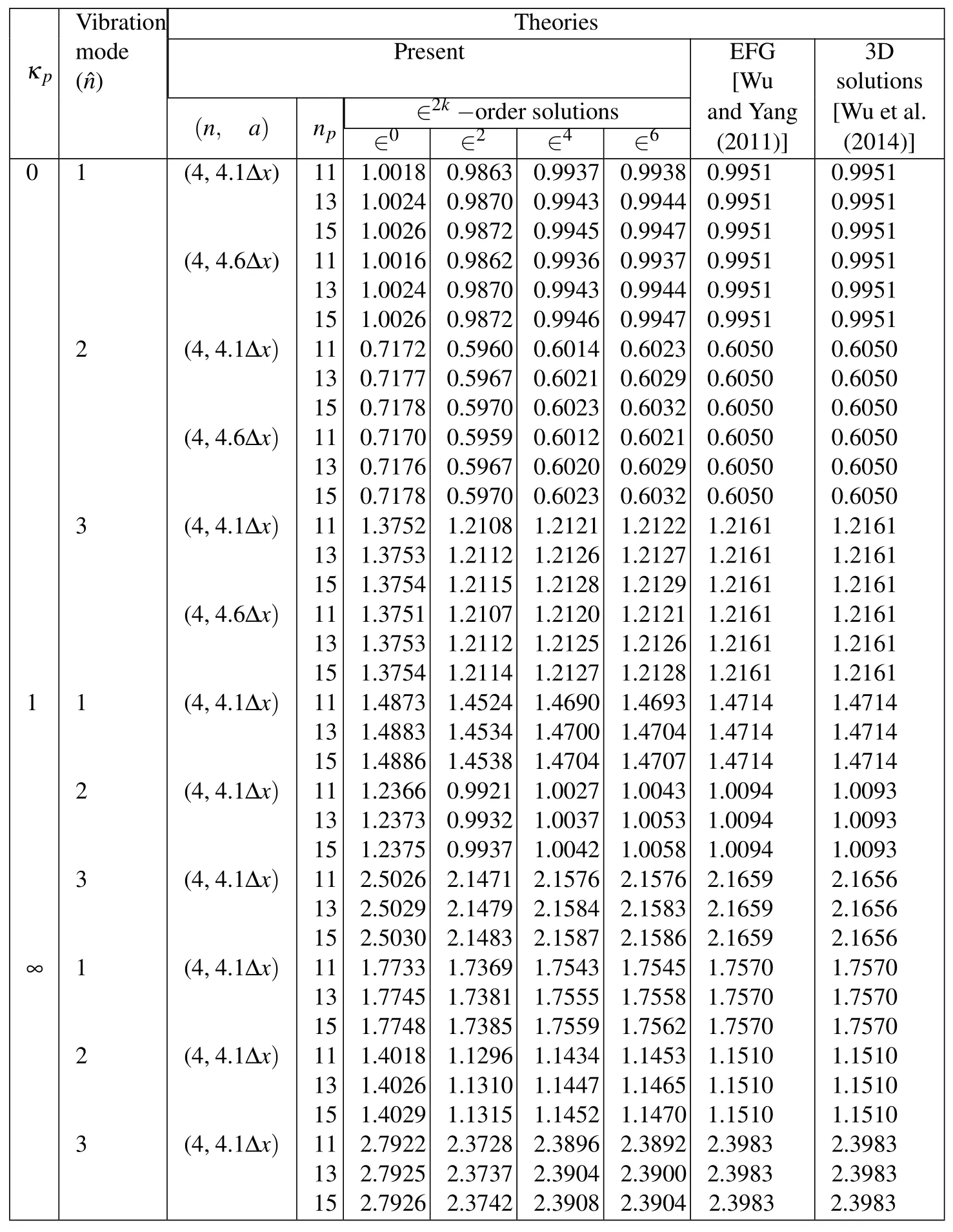
Table 1: The convergence study with regard to the results of lowest frequency parameters of simply-supported,sandwich FGM cylinders for different vibration modes(L/R=5,R/2h=10,h1:h2:h3=2h/3:2h/3:2h/3,=ωR2(2h)).
κp Vibration Theories mode(ˆn)Present EFG[Wu 3D solutions(n,a)np ∈2k−order solutions and Yang [Wu et al.∈0∈2∈4∈6(2011)](2014)]0 1∞1 2 3 123123(4,4.1Δx)(4,4.6Δx)(4,4.1Δx)(4,4.6Δx)(4,4.1Δx)(4,4.6Δx)(4,4.1Δx)(4,4.1Δx)(4,4.1Δx)(4,4.1Δx)(4,4.1Δx)(4,4.1Δx)11 13 15 11 13 15 11 13 15 11 13 15 11 13 15 11 13 15 11 13 15 11 13 15 11 13 15 11 13 15 11 13 15 11 13 15 1.0018 1.0024 1.0026 1.0016 1.0024 1.0026 0.7172 0.7177 0.7178 0.7170 0.7176 0.7178 1.3752 1.3753 1.3754 1.3751 1.3753 1.3754 1.4873 1.4883 1.4886 1.2366 1.2373 1.2375 2.5026 2.5029 2.5030 1.7733 1.7745 1.7748 1.4018 1.4026 1.4029 2.7922 2.7925 2.7926 0.9863 0.9870 0.9872 0.9862 0.9870 0.9872 0.5960 0.5967 0.5970 0.5959 0.5967 0.5970 1.2108 1.2112 1.2115 1.2107 1.2112 1.2114 1.4524 1.4534 1.4538 0.9921 0.9932 0.9937 2.1471 2.1479 2.1483 1.7369 1.7381 1.7385 1.1296 1.1310 1.1315 2.3728 2.3737 2.3742 0.9937 0.9943 0.9945 0.9936 0.9943 0.9946 0.6014 0.6021 0.6023 0.6012 0.6020 0.6023 1.2121 1.2126 1.2128 1.2120 1.2125 1.2127 1.4690 1.4700 1.4704 1.0027 1.0037 1.0042 2.1576 2.1584 2.1587 1.7543 1.7555 1.7559 1.1434 1.1447 1.1452 2.3896 2.3904 2.3908 0.9938 0.9944 0.9947 0.9937 0.9944 0.9947 0.6023 0.6029 0.6032 0.6021 0.6029 0.6032 1.2122 1.2127 1.2129 1.2121 1.2126 1.2128 1.4693 1.4704 1.4707 1.0043 1.0053 1.0058 2.1576 2.1583 2.1586 1.7545 1.7558 1.7562 1.1453 1.1465 1.1470 2.3892 2.3900 2.3904 0.9951 0.9951 0.9951 0.9951 0.9951 0.9951 0.6050 0.6050 0.6050 0.6050 0.6050 0.6050 1.2161 1.2161 1.2161 1.2161 1.2161 1.2161 1.4714 1.4714 1.4714 1.0094 1.0094 1.0094 2.1659 2.1659 2.1659 1.7570 1.7570 1.7570 1.1510 1.1510 1.1510 2.3983 2.3983 2.3983 0.9951 0.9951 0.9951 0.9951 0.9951 0.9951 0.6050 0.6050 0.6050 0.6050 0.6050 0.6050 1.2161 1.2161 1.2161 1.2161 1.2161 1.2161 1.4714 1.4714 1.4714 1.0093 1.0093 1.0093 2.1656 2.1656 2.1656 1.7570 1.7570 1.7570 1.1510 1.1510 1.1510 2.3983 2.3983 2.3983
It can be seen in Table 1 that the convergence rate for the asymptotic solutions of the lowest frequency of the cylinders is rapid,and the convergent solutions are in excellent agreement with the quasi-and exact-3D solutions available in the literature,in which the highest order of base functions(n)is taken asn=4,the total number of selected sampling nodes(np)isnp=11,13 and 15,the radius of the infl uence zone(a)for each node is eithera=4.1Δxora=4.6Δx,and Δx=L/(np−1).
The results show that the relative errors between the 15-node∈4-order solutions with(n,a)=(4,4.1Δx)and the exact-3D ones[Wu et al.(2014)]are less than 0.6%,and the set of related parameters is thus used in the next example,such asn=4,a=4.1Δx,andnp=15.It is also shown that for a particular vibration mode,the natural frequency parameter increases when the material-property gradient index becomes larger,which means the sandwich cylinder becomes stiffer;and the fundamental frequency parameter occurs atnˆ=2 for these moderately thick FGM sandwich cylinders.
8.2 Sandwich cylinders with an embedded FGM core
The dynamic responses of sandwich FGM circular hollow cylinders,consisting of two homogeneous face-sheets and an embedded FGM core,with combinations of simply-supported and clamped edges are investigated,and the configuration,cylindrical coordinate systems and layer-up sequence of the cylinder are shown in Figs.1(a)and 1(c).The effective engineering constants of each layer are evaluated by using the rule of mixtures[Hill(1965)]and Mori-Tanaka scheme[Mori and Tanaka(1973)],and these are written,as follows:
(a)The rule of mixtures,
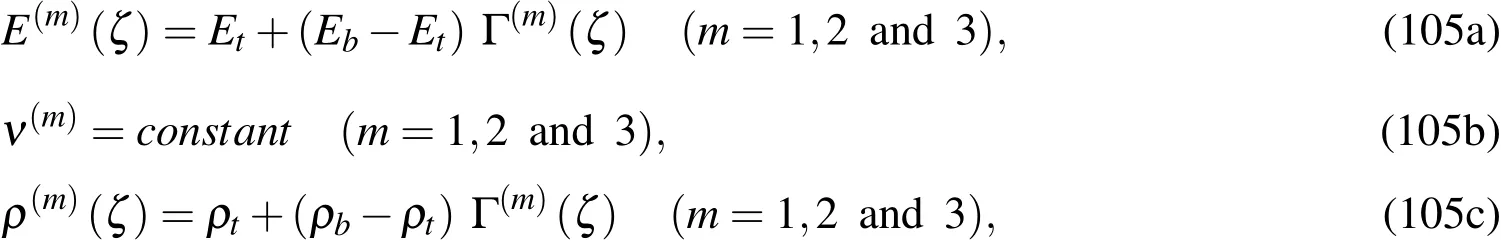
whereEtandEbdenote the Young’s modulus of the material at the mid-surface of the core-layer and that of the face-sheets,respectively,for whichEtandEbare the same values as those used in Example 8.1;ν(m)(m=1_3)are taken to be 0.3;and Γ(m)(m=1_3)are the volume fractions of the constituents of the cylinder,and are given by

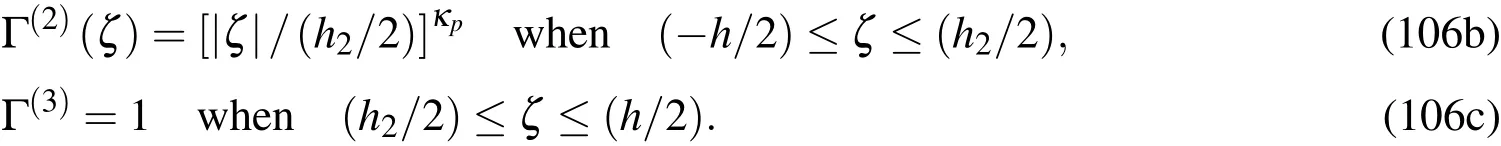
(b)Mori-Tanaka scheme,
The effective material properties of the FGM core(i.e.,the second layer)are evaluated using the Mori-Tanaka formula[Ramirez et al.(2006)],and are written as follows:
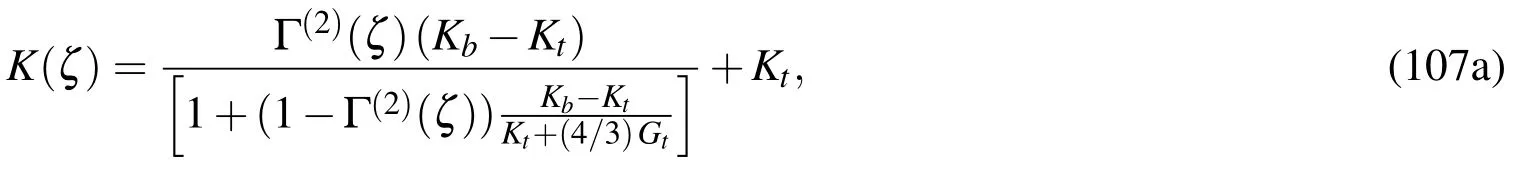

It is apparent that whenκp=0,Γ(2)=1,this sandwich FGM cylinder is reduced to a single-layered homogeneous alumina cylinder;while whenκp=∞,Γ(2)=0,it is reduced to a sandwich homogeneous cylinder(i.e.,sandwich[alumina/aluminum/alumina]ones).Figure2 shows the through-thickness distributions of the Young’s modulus evaluated by the rule of mixtures and Mori-Tanaka scheme for a particular case,in whichκp=2 and 4,andh1:h2:h3=0.2h:1.6h:0.2h.The results show that the material properties evaluated by using the rule of mixtures are greater than those evaluated by using Mori-Tanaka scheme,which means that the rule of mixtures gives a stiffer FGM layer than Mori-Tanaka scheme does,although these values are not much different from each other.In addition,the set of dimensionless frequency parameters used in Example 8.1 is also used in this example.
Table 2 shows the asymptotic DRK-based meshless solutions for the lowest frequency parameters of sandwich FGM cylinders with different boundary conditions,thickness ratios for each layer and material-property gradient indices,in whichR/2h=10,L/R=5,(,)=(1,2),h1:h2:h3=0.8h:0.4h:0.8hand 0.2h:1.6h:0.2h,andκp=0,2,4 and∞.It can be seen in Table 2 that the asymptotic DRK-based meshless solutions converge rapidly,and the relative errors between the∈4-order solutions and exact 3D ones[Wu et al.(2014)]are less than 0.6%for the moderately thick cylinder with simply-supported edges.The magnitude order of the lowest frequencies of the cylinders for different boundary conditions is CC>SC>SS,and that for using different material-property models is the rule of mixtures>Mori-Tanakascheme,in which“>”means the cylinder is stiffer and the corresponding natural frequency parameter is greater.
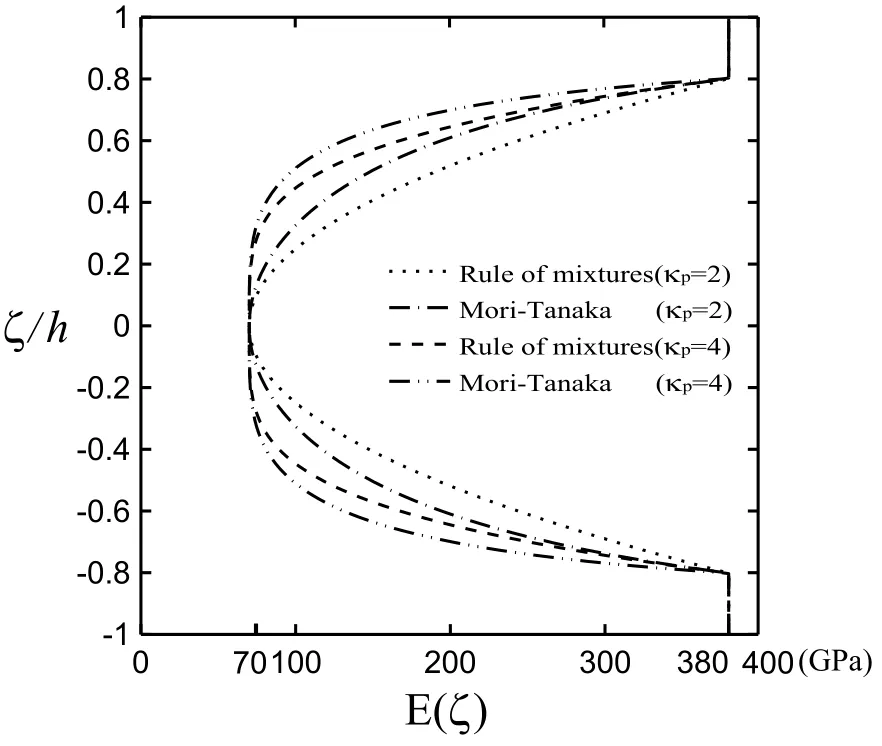
Figure 2: Through-thickness distributions of Young’s modulus of a sandwich cylinder with an embedded FGM core,and estimated by using the rule of mixtures and the Mori-Tanaka scheme,in which κp=2 and 4,and h1:h2:h3=0.2h:1.6h:0.2h.
Figures 3(a)-3(c)show variations of the lowest frequency parameters of sandwich FGM cylinders with the half-wave-number()for the SS,SC and CC edges,respectively,in which a set of parameters,R/2h=10,L/R=5,h1:h2:h3=0.2h:1.6h:0.2h,κp=0,2,4 and∞,and=0-10,and the Mori-Tanaka scheme is used.It can be seen in Figs.3(a)-3(c)that at first the frequency parameter gradually decreases,and then it monotonically increases again when>2.The variation patterns for different boundary conditions are shown to be similar to one another,except that the magnitude order of the lowest frequency parameters are CC>SC>SS,even though the deviations among them are hard to distinguish from the figures.In addition,the results also show when the material-property gradient index increases,the frequency parameter becomes lower,which means the gross stiffness of the cylinder becomes softer.
Tables 3 and 4 show the asymptotic DRK-based meshless solutions for the lowest frequency parameters of sandwich FGM cylinders for a particular vibration mode(,)=(1,2)and with different values of the ratios of radius-to-thickness(R/2h)and length-to-radius(L/R),respectively,in whichκp=3,L/R=10,R/2h=5,10,50 and 100 in Table 3,andκp=3,R/2h=10,L/R=2,5,10 and 100 in Table 4.When we convert the frequency parameter()to the natural frequency(ω),the resultsshow that the natural frequency decreases when the cylinder becomes thinner and longer.

Table 2:The lowest freq uency parameters of FG M sandwich1,cylind ers with different5; boun dary conditions,thick ness ratios for each layer and material-p ro perty gradient indices(ˆm=ˆn=2,R/2h=1 0,L/R=¯ω=ωR 2 ρb/Eb/(2h).κp Theories 0.8h:0.4h:0.8h 0.2h:1.6 h:0.2h SS SC CC SS SC CC Ru le of mixtures Mori-Tanaka Rule of mixtures 97 02 31 48 Mo ri-Tanaka Rule of mixtu res 10 80 18 31 Mori-Tanaka Ru le of mixtures Mori-Tanaka Rule of mixtures Mori-Tanaka Rule of mixtu res 10 80 18 31 Mo ri-Tanaka 0 Present∈0-order 1.4117 1.41 17 42 47 64 97 97 84 98 16 52 09 61 80 98 34 26 26 53 71 07 1.60 1.6097 1.84 1.8410 1.4117 1.41 17 42 47 64 97 82 80 87 03 40 97 21 27 43 78 66 54 51 65 97 1.6097 1.6097 1.84 1.8410∈2−order 1.1742 1.17 1.40 1.4002 1.65 1.6580 1.1742 1.17 1.4002 1.4002 1.65 1.6580∈4−order 1.1847 1.18 1.41 1.4131 1.67 1.6718 1.1847 1.18 1.4131 1.4131 1.67 1.6718∈6−order 1.1864 1.18 1.41 1.4148 1.67 1.6731 1.1864 1.18 1.4148 1.4148 1.67 1.6731 3D solutions[Wu et al.(2014)]1.1897 1.18 NA NA NA NA 1.1897 1.18 NA NA NA NA 2 Present∈0-order 1.4132 1.40 1.59 9 63 02 20 1.5937 1.81 78 17 67 82 1.8105 1.3268 1.27 1.4749 1.4186 1.65 21 23 79 95 1.5872∈2−order 1.1628 1.15 1.37 1.3699 1.62 1.6133 1.0683 1.02 1.2405 1.1914 1.44 1.3836∈4−order 1.1741 1.16 1.39 1.3839 1.63 1.6285 1.0795 1.03 1.2546 1.2049 1.45 1.3986∈6−order 1.1759 1.17 1.39 1.3857 1.63 1.6299 1.0812 1.04 1.2564 1.2066 1.45 1.4001 3D solutions[Wu et al.(2014)]1.1794 1.17 NA NA NA NA 1.0849 1.04 NA NA NA NA 4 Present∈0-order 1.4132 1.41 1.59 65 01 45 63 1.5929 1.81 26 29 85 00 1.8078 1.2806 1.23 1.4168 1.3709 1.58 07 08 64 79 1.5290∈2−order 1.1591 1.15 1.37 1.3658 1.61 1.6073 1.0245 0.99 1.1834 1.1452 1.37 1.3259∈4−order 1.1709 1.16 1.38 1.3803 1.62 1.6230 1.0356 1.00 1.1974 1.1586 1.38 1.3409∈6−order 1.1727 1.16 1.38 1.3821 1.63 1.6245 1.0373 1.00 1.1992 1.1603 1.38 1.3424 3D solutions[Wu et al.(2014)]1.1763 1.17 NA NA NA NA 1.0409 1.00 NA NA NA NA∞Present∈0-order 1.4126 1.41 1.59 21 96 51 69 1.5921 1.80 42 86 53 68 1.8042 1.1466 1.14 1.2648 1.2648 1.40 73 68 05 19 1.4073∈2−order 1.1526 1.15 1.35 1.3596 1.59 1.5986 0.9154 0.91 1.0535 1.0535 1.21 1.2168∈4−order 1.1653 1.16 1.37 1.3751 1.61 1.6153 0.9251 0.92 1.0657 1.0657 1.23 1.2305∈6−order 1.1671 1.16 1.37 1.3769 1.61 1.6168 0.9265 0.92 1.0672 1.0672 1.23 1.2319 3D solutions[Wu et al.(2014)]1.1707 1.17 NA NA NA NA 0.9297 0.92 NA NA NA NA

T a b l e 3:T h e l o w e s t f r e q u e n c y p a r a m e t e r s o f s i m p l y s u p p o r t e d,F G M s a n d w i c h c y l i n d e r s w i t h d i f f e r e n t m i d-s u r f a c e r a d i u s-t o-t h i c k n e s s r a t i o s a n d t h i c k n e s s r a t i o s f o r e a c h l a y e r(ˆm=1,ˆn=2,κp=3,L/R=1 0,¯ω=ω R2 ρb/Eb/(2 h)).R/2 h T h e o r i e s 0.8 h:0.4 h:0.8 h 0.2 h:1.6 h:0.2 h S S S C C C S S S C C C R u l e o f m i x-t u r e s M o r i-T a n a k a R u l eo f m i x-t u r e s M o r i-T a n a k a R u l eo f m i x-t u r e s M o r i-T a n a k a R u l eo f m i x-t u r e s M o r i-T a n a k a R u l eo f m i x-t u r e s M o r i-T a n a k a R u l eo f m i x-t u r e s M o r i-T a n a k a 5 P r e s e n t∈0-o r d e r 1.1 2 7 2 1.1 2 6 7 1.1 3 6 3 1.1 3 5 8 1.1 4 9 1 1.1 4 8 5 1.0 7 8 6 1.0 4 3 6 1.0 8 5 9 1.0 5 0 5 1.0 9 5 7 1.0 5 9 9∈2−order 0.8027 0.7998 0.8134 0.8105 0.8291 0.8261 0.7448 0.7218 0.7531 0.7298 0.7650 0.7412∈4−order 0.8124 0.8101 0.8236 0.8213 0.8400 0.8376 0.7614 0.7372 0.7701 0.7456 0.7826 0.7576∈6−order 0.8130 0.8107 0.8243 0.8220 0.8409 0.8385 0.7613 0.7373 0.7701 0.7457 0.7828 0.7578 3 D s o l u t i o n s[W u e t a l.(2 0 1 4)]0.8 1 9 7 0.8 1 7 6 N A N A N A N A 0.7 6 8 6 0.7 4 4 2 N A N A N A N A 1 0 P r e s e n t∈0-o r d e r 1.1 4 2 6 1.1 4 2 0 1.1 6 9 3 1.1 6 8 3 1.2 0 9 6 1.2 0 8 2 1.0 8 9 9 1.0 5 4 3 1.1 0 9 6 1.0 7 3 1 1.1 3 9 1 1.1 0 1 1∈2−order 0.8560 0.8548 0.8882 0.8867 0.9375 0.9355 0.8084 0.7823 0.8322 0.8050 0.8684 0.8395∈4−order 0.8590 0.8579 0.8925 0.8911 0.9438 0.9419 0.8123 0.7859 0.8370 0.8095 0.8748 0.8455∈6−order 0.8595 0.8584 0.8933 0.8920 0.9449 0.9431 0.8127 0.7864 0.8377 0.8102 0.8758 0.8464 3 D s o l u t i o n s[W u e t a l.(2 0 1 4)]0.8 6 2 7 0.8 6 1 6 N A N A N A N A 0.8 1 6 0 0.7 8 9 5 N A N A N A N A 5 0 P r e s e n t∈0-o r d e r 1.5 2 4 2 1.5 1 9 8 1.9 1 6 0 1.9 0 8 4 2.4 3 0 1 2.4 1 8 7 1.3 6 8 8 1.3 1 9 9 1.6 6 8 0 1.6 0 5 4 2.0 7 0 5 1.9 8 9 9∈2−order 1.3174 1.3126 1.7508 1.7427 2.2998 2.2879 1.1572 1.1146 1.4937 1.4306 1.9300 1.8532∈4−order 1.3292 1.3244 1.7644 1.7562 2.3126 2.3007 1.1673 1.1244 1.5065 1.4482 1.9428 1.8655∈6−order 1.3308 1.3260 1.7655 1.7574 2.3133 2.3014 1.1689 1.1259 1.5078 1.4495 1.9437 1.8664 3 D s o l u t i o n s[W u e t a l.(2 0 1 4)]1.3 3 1 4 1.3 2 6 5 N A N A N A N A 1.1 6 9 5 1.1 2 6 5 N A N A N A N A 1 0 0 P r e s e n t∈0-o r d e r 2.3 4 3 7 2.3 3 3 0 3.2 9 5 4 3.2 7 8 2 4.4 4 7 3 4.4 2 2 7 2.0 0 1 5 1.9 2 4 4 2.7 6 0 1 2.6 5 0 0 3.6 9 0 5 3.5 4 0 6∈2−order 2.2094 2.1981 3.1995 3.1818 4.3762 4.3513 1.8570 1.7838 2.6550 2.5475 3.6118 3.4639∈4−order 2.2223 2.2111 3.2101 3.1924 4.3845 4.3596 1.8699 1.7962 2.6661 2.5583 3.6208 3.4726∈6−order 2.2230 2.2118 3.2104 3.1928 4.3846 4.3597 1.8708 1.7971 2.6665 2.5587 3.6210 3.4728 3 D s o l u t i o n s[W u e t a l.(2 0 1 4)]2.2 2 3 0 2.2 1 1 8 N A N A N A N A 1.8 7 0 8 1.7 9 7 2 N A N A N A N A

Table4:T he lowestfrequencyparam etersofsimplysupported2,κp,F GMs=3and wich cylind ersw ithdifferentlength-to-mid-surface radius ratios and thickness ratios for each layer(ˆm=1,ˆn=,R/2h=10,¯ω=ωR 2 ρb/Eb/(2h).L/R Theories 0.8h:0.4h:0.8h 0.2h:1.6h:0.2h SS SC CC SS SC CC Ru le of mixtures Mori-Tanaka Rule of mixtu res 50 12 49 49 Mo ri-Tanaka Rule of mixtu res Mori-Tanaka Ru le of mixtures Mori-Tanaka Rule of mixtures 01 62 31 27 Mo ri-Tanaka Rule of mixtu res 17 66 31 16 Mo ri-Tanaka 2 Present∈0-order 3.7125 3.6956 4.11 4.0973 4.5982 4.5796 3.1646 3.04 37 51 16 21 86 55 65 71 87 23 43 23 59 64 95 28 11 35 37 68 3.52 3.3894 3.95 3.8089∈2−order 3.5673 3.5492 3.98 3.9622 4.4751 4.4551 3.0000 2.88 3.36 3.2413 3.80 3.6695∈4−order 3.5819 3.5641 3.99 3.9762 4.4877 4.4681 3.0174 2.90 3.38 3.2574 3.82 3.6852∈6−order)]3.5823 3.5644 3.99 3.9762 4.4873 4.4676 3.0179 2.90 3.38 3.2570 3.82 3.6839 3D solutions[Wu et al.(2014 3.5888 3.5711 NA NA NA NA 3.0245 2.90 NA NA NA NA 5 Present∈0-order 1.4132 1.4104 1.59 65 15 57 75 1.5923 1.8118 1.8060 1.3004 1.25 1.44 04 59 00 18 1.3895 1.60 79 73 29 45 1.5501∈2−order 1.1606 1.1570 1.37 1.3663 1.6134 1.6067 1.0427 1.00 1.20 1.1627 1.39 1.3463∈4−order 1.1722 1.1687 1.38 1.3807 1.6288 1.6222 1.0539 1.01 1.22 1.1761 1.41 1.3613∈6−order)]1.1740 1.1705 1.38 1.3825 1.6303 1.6237 1.0556 1.01 1.22 1.1779 1.41 1.3628 3D solutions[Wu et al.(2014 1.1775 1.1741 NA NA NA NA 1.0592 1.02 NA NA NA NA 10 Present∈0-order 1.1426 1.1420 1.16 93 82 25 33 1.1683 1.2096 1.2082 1.0899 1.05 1.10 96 22 70 77 1.0731 1.13 91 84 48 58 1.1011∈2−order 0.8560 0.8548 0.88 0.8867 0.9375 0.9355 0.8084 0.78 0.83 0.8050 0.86 0.8395∈4−order 0.8590 0.8579 0.89 0.8911 0.9438 0.9419 0.8123 0.78 0.83 0.8095 0.87 0.8455∈6−order)]0.8595 0.8584 0.89 0.8920 0.9449 0.9431 0.8127 0.78 0.83 0.8102 0.87 0.8464 3D solutions[Wu et al.(2014 0.8627 0.8616 NA NA NA NA 0.8160 0.78 NA NA NA NA 10 0 Present∈0-order 1.1034 1.1029 1.10 34 57 73 75 1.1029 1.1034 1.1029 1.0570 1.02 1.05 70 60 87 89 1.0228 1.05 70 60 87 89 1.0228∈2−order 0.8157 0.8147 0.81 0.8148 0.8157 0.8148 0.7759 0.75 0.77 0.7511 0.77 0.7511∈4−order 0.8173 0.8164 0.81 0.8165 0.8174 0.8165 0.7786 0.75 0.77 0.7536 0.77 0.7536∈6−order)]0.8174 0.8166 0.81 0.8167 0.8175 0.8167 0.7788 0.75 0.77 0.7538 0.77 0.7539 3D solutions[Wu et al.(2014 0.8205 0.8197 NA NA NA NA 0.7820 0.75 NA NA NA NA
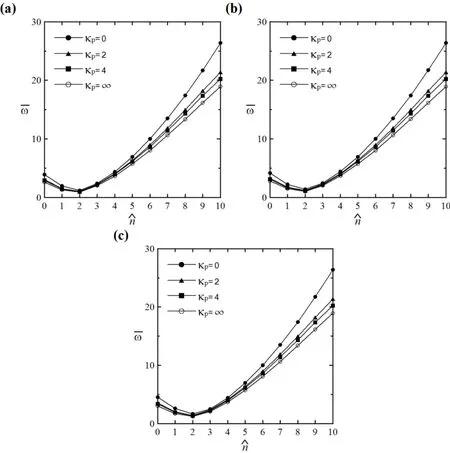
Figure 3: Variations of the lowest frequencies of sandwich FGM cylinders with different vibration modes and different values of material-property gradient indices and using the Mori-Tanaka scheme;(a)SS,(b)SC,(c)CC edges.
Figure 4 shows the∈4-order DRK solutions for the through-thickness distributions of various modal variables induced at a certain crucial section of a simply supported,FGM sandwich cylinder,inwhichL/R=5,R/(2h)=10,h1:h2:h3=0.4h:1.2h:0.4handκp=3,and the material properties of the embedded FGM core are estimated by using the rule of mixtures and the Mori-Tanaka scheme.It can be seen in Fig.4 that the distributions of various modal variables through the thickness coordinate obtained by using the rule of mixtures closely agree with those obtained by using the Mori-Tanaka scheme.The through-thickness distributions of in-and
out-of surface displacement components appear to be globally linear and layerwise parabolic polynomial variations,respectively.The through-thickness distributions of in-surface and transverse stress components appear to be linear and parabolic polynomial variations in the homogeneous face sheets,respectively,while they all appear to be higher-order polynomial variations in the FGM core.Moreover,the asymptotic DRK solutions satisfy the boundary conditions at lateral surfaces and the continuity conditions of displacement and transverse stress components at interfaces between adjacent layers,which is difficult to achieve for various 2D displacement-based shell theories.
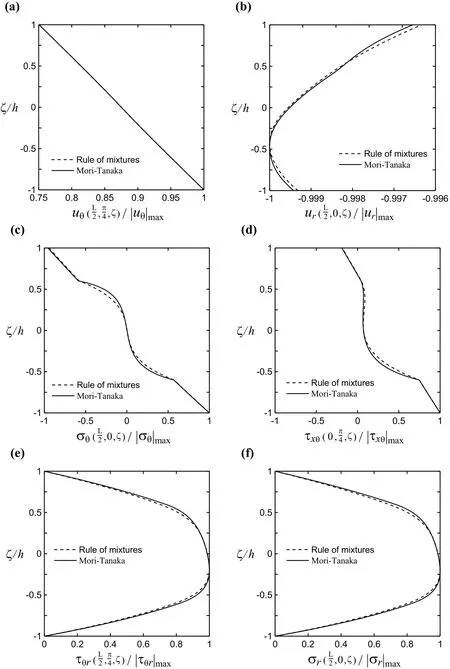
Figure 4: Through-thickness distributions of various modal variables for simply supported,sandwich FGM cylinder with different material models,in which R/2h=10,L/R=5,h1:h2:h3=0.4h:1.2h:0.4h,=2,and κp=3.
9 Conclusions
On the basis of the multiple time scale and meshless DRK methods,in this article we developed an asymptotic DRK-based meshless formulation for the quasi-3D free vibration analysis of FGM sandwich circular hollow cylinders with combinations of simply-supported and clamped edges.In the illustrative examples,it is shown that these asymptotic DRK solutions converge rapidly,and are in excellent agreement with the approximate and exact 3D solutions of simply-supported,sandwich FGM cylinders available in the literature, and those for the cases of SC and CC edge conditions can be used as a reference for assessing the solutions obtained using other 2D and 3D methodologies and numerical techniques.It is also seen in the examples that the natural frequency decreases when the cylinder becomes thinner and longer,and the magnitude order of the natural frequency for different boundary conditions is CC>SC>SS,and that for using different material-property models is the rule of mixtures>Mori-Tanaka scheme.The through-thickness distributions of the in-and out-of-surface modal variables of sandwich FGM cylinders in the free vibration problems have been observed,and the results can be provided as a reference for making the kinetic and kinematic assumptions a priori when an advanced 2D FGM shell theory is to be developed.
Acknowledgement:This work was supported by the Ministry of Science and Technology of the Republic of China through Grant MOST 103-2221-E-006-064-MY3.
Atluri,S.N.;Shen,S.(2002):The Meshless Local Petro-Galerkin(MLPG)Method.Encino,Tech Science Press.
Atluri,S.N.;Zhu,T.(1998):A new meshless local Petro-Galerkin(MLPG)approach in computational mechanics.Computational Mechanics,vol.22,pp.117-127.
Belytschko,T.;Krongauz,Y.;Organ,D.;Fleming,M.;Krysl,P.(1996):Meshless methods:an overview and recent developments.Computer Methods in Applied Mechanics and Engineering,vol.139,pp.3-47.
Brischetto,S.(2013):Exact elasticity solutions for natural frequencies of functionally graded simply-supported structures.CMES-Computer Modeling in Engineering&Sciences,vol.95,pp.391-430.
Carrera,E.(2000):An assessment of mixed and classical theories on global and local response of multilayered orthotropic plates.Composite Structures,vol.50,pp.183-198.
Carrera,E.(2003):Historical review of zig-zag theories for multilayered plates and shells.Applied Mechanics Reviews,vol.56,pp.287-308.
Carrera,E.;Brischetto,S.(2009):A survey with numerical assessment of classical and re fi ned theories for the analysis of sandwich plates.Applied Mechanics Reviews,vol.62,pp.1-17.
Carrera,E.;Ciuffreda,A.(2005):A uni fi ed formulation to assess theories of multilayered plates for various bending problems.Composite Structures,vol.69,pp.271-293.
Carrera,E.;Brischetto,S.;Robaldo,A.(2008):Variable kinematic model for the analysis of functionally graded material plates.AIAA Journal,vol.46,pp.194-203.
Carrera,E.;Brischetto,S.;Cinefra,M.;Soave,M.(2010):Re fi ned and advanced models for multilayered plates and shells embedding functionally graded material layers.Mechanics of Advanced Materials and Structures,vol.17,pp.603-621.
Chen,W.Q.;Ding,H.J.(2002):On free vibration of a functionally graded piezoelectric rectangular plate.Acta Mechanica,vol.153,pp.207-216.
Chen,S.M.;Wu,C.P.;Wang,Y.M.(2011):AHermite DRK interpolation-based collocation method for the analysis of Bernoulli-Euler beams and Kirchhoff-Love plates.Computational Mechanics,vol.47,pp.425-453.
Cinefra,M.;Belouettar,S.;Soave,M.;Carrera,E.(2010):Variable kinematic models applied to free-vibration analysis of functionally graded material shells.European Journal of Mechanics A-Solids,vol.29,pp.1078-1087.
Cinefra,M.;Carrera,E.;Brischetto,S.;Belouettar,S.(2010):Ther momechanical analysis of functionally graded shells.Journal of Thermal Stresses,vol.33,pp.942-963.
Dube,G.P.;Kapuria,S.;Dumir,P.C.(1996a):Exact piezother moelastic solu-tion of simply-supported orthotropic circular cylindrical panel in cylindrical bending.Archive of Applied Mechanics,vol.66,pp.537-554.
Dube,G.P.;Kapuria,S.;Dumir,P.C.(1996b):Exact piezothermoelastic solution of simply-supported orthotropic fl at panel in cylindrical bending.International Journal of Mechanical Sciences,vol.38,pp.1161-1177.
Dumir,P.C.;Dube,G.P.;Kapuria,S.(1997):Exact piezoelectric solution of simply-supported orthotropic circular cylindrical panel in cylindrical bending.International Journal of Solids and Structures,vol.34,pp.685-702.
Ferreira,A.J.M.;Roque,C.M.C.;Martins,P.A.L.S.(2003):Analysis of composite plates using higher-order shear deformation theory and a finite point formulation based on the multiquadric radial basis function.Composites Part BEngineering,vol.34,pp.627-636.
Heyliger,P.;Brooks,S.(1995):Free vibration of piezoelectric laminates in cylindrical bending.International Journal of Solids and Structures,vol.32,pp.2945-2960.
Heyliger,P.;Brooks,S.(1996):Exact solutions for laminated piezoelectric plates in cylindrical bending.Journal of Applied Mechanics,vol.63,pp.903-910.
Hill,R.(1965):A self-consistent mechanics of composite materials.Journal of the Mechanics and Physics of Solids,vol.13,pp.213-222.
Hosseini,S.M.;Sladek,J.;Sladek,V.(2011):Meshless local Petro-Galerkin method for coupled thermoelasticity analysis of a functionally graded thick hollow cylinder.Engineering Analysis with Boundary Elements,vol.35,pp.827-835.
Li,S.;Liu,W.K.(2004):Meshfree Particle Methods.Berlin:Springer.
Liew,K.M.;Lei,Z.X.;Zhang,L.W.(2015):Mechanical analysis of functionally graded carbon nanotube reinforced composites:A review.Composite Structures,vol.120,pp.90-97.
Liew,K.M.;Zhao,X.;Ferreira,A.J.M.(2011):A review of meshless methods for laminated and functionally graded plates and shells.Composite Structures,vol.93,pp.2031-2041.
Mori,T.;Tanaka,K.(1973):Average stress in matrix and average elastic energy of materials with mis fi tting inclusions.Acta Metallurgica,vol.21,pp.571-574.
Moussavinezhad,S.M.;Shahabian,F.;Hosseini,S.M.(2013):Twodimensional elastic wave propagation analysis in finite length FG thick hollow cylinders with 2D nonlinear grading patterns using MLPG method.Computer Methods in Applied Mechanics and Engineering,vol.91,pp.177-204.
Nayfeh,A.H.(1981):Introduction to Perturbation Techniques.New York:John Wiley&Sons.
Ramirez,F.;Heyliger,P.R,;Pan,E.(2006):Static analysis of functionally graded elastic anisotropic plates using a discrete layer approach.Composites Part B-Engineering,vol.37,pp.10-20.
Roque,C.M.C.;Ferreira,A.J.M.;Jorge,R.M.N.(2005):Modeling of composite and sandwich plates by a trigonometric layerwise deformation theory and radial basis functions.Composites Part B-Engineering,vol.36,pp.559-572.
Saravanos,D.A.;Heyliger,P.G.(1999):Mechanics and computational models for laminated piezoelectric beams,plates,and shells.Applied Mechanics Reviews,vol.52,pp.305-320.
Sladek,J.;Sladek,V.;Zhang,C.(2003):Application of meshless local Petro-Galerkin(MLPG)method to elastodynamic problems in continuously nonhomogeneous solids.CMES-Computer Modeling in Engineering&Sciences,vol.4,pp.637-647.
Sladek,J.;Sladek,V.;Krivacek,J.;Aliabadi,M.H.(2007):Local boundary integral equations for orthotropic shallow shells.International Journal of Solids and Structures,vol.44,pp.2285-2303.
Sladek,J.;Sladek,V.;Solek,P.;Wen,P.H.(2008):Thermal bending of Reissner-Mindl in plates by the MLPG.Computer Methods in Applied Mechanics and Engineering,vol.28,pp.57-76.
Sladek,J.;Sladek,V.;Stanak,P.;Zhang,Ch.(2010):Meshless local Petro-Galerkin(MLPG)method for laminate plates under dynamic loading.CMCComputers,Materials,&Continua,vol.15,pp.1-26.
Sladek,J.;Stanak,P.;Han,Z.D.;Sladek,V.;Atluri,S.N.(2013):Applications of the MLPG method in Engineering and Sciences:a review.Computer Methods in Applied Mechanics and Engineering,vol.92,pp.423-475.
Sladek,J.;Sladek,V.;Zhang,C.H.;Krivacek,J.;Wen,P.H.(2006):Analysis of orthotropic thick plates by meshless local Petro-Galerkin(MLPG)method.International Journal for Numerical Methods in Engineering,vol.13,pp.2830-2850.
Soldatos,K.P.;Hadjigeorgiou,V.P.(1990):Three-dimensional solution of the free vibration problem of homogeneous isotropic cylindrical shells and panels.Journal of Sound and Vibration,vol.137,pp.369-384.
Swaminathan,K.;Naveenkumar,D.T.,Zenkour,A.M.;Carrera,E.(2015):Stress,vibration and buckling analyses of FGM plates-A state-of-the art review.Composite Structures,vol.120,pp.10-31.
Wang,Y.M.;Chen,S.M.;Wu,C.P.(2010):A meshless collocation method based on the differential reproducing kernel interpolation.Computational Mechan-ics,vol.45,pp.585-606.
Wu,C.P.;Li,H.Y.(2010):RMVT-and PVD-based finite layer methods for the quasi-3D free vibration analysis of multilayered composite and FGM plates.CMC-Computers,Materials,&Continua,vol.19,pp.155-198.
Wu,C.P.;Li,H.Y.(2013):An RMVT-based finite rectangular prism method for the 3D analysis of sandwich FGM plates with various boundary conditions.CMCComputers,Materials,&Continua,vol.34,pp.27-61.
Wu,C.P.;Liu,K.Y.(2007):A state space approach for the analysis of doubly curved functionally graded elastic and piezoelectric shells.CMC-Computers,Materials,&Continua,vol.6,pp.177-199.
Wu,C.P.;Syu,Y.S.(2007):Exact solutions of functionally graded piezoelectric shells under cylindrical bending.International Journal of Solids and Structures,vol.44,pp.6450-6072.
Wu,C.P.;Tsai,Y.H.(2009):Cylindrical bending vibration of functionally graded piezoelectric shells using the method of perturbation.Journal of Engineering Mathematics,vol.63,pp.95-119.
Wu,C.P.;Tsai,Y.H.(2010):Dynamic responses of functionally graded magnet oelectro-elastic shells with closed-circuit surface conditions using the method of multiple scales.European Journal of Mechanics A-Solids,vol.29,pp.166-181.
Wu,C.P.;Tsai,T.C.(2012):Exact solutions of functionally graded piezoelectric material sandwich cylinders by a modified Pagano method.Applied Mathematical Modelling,vol.36,pp.1910-1930.
Wu,C.P.;Yang,S.W.(2011):A semi-analytical element-free Galerkin method for the 3D free vibration analysis of multilayered FGM circular hollow cylinders.Journal of Intelligent Material Systems and Structures,vol.22,pp.1993-2007.
Wu,C.P.;Chiu,K.H.;Wang,Y.M.(2008):A review on the three-dimensional analytical approaches of multilayered and functionally graded piezoelectric plates and shells.CMC-Computers,Materials,&Continua,vol.8,pp.93-132.
Wu,C.P.;Jiang,R.Y.;Tu,S.Y.(2014):Exact solutions for the stability and free vibration of multilayered functionally graded material hollow cylinders under axial compression.CMC-Computers,Materials,&Continua,vol.42,pp.111-152.
Wu,C.P.;Tarn,J.Q.;Chi,S.M.(1996a):Three-dimensional analysis of doubly curved laminated shells.Journal of Engineering Mechanics,vol.122,pp.391-401.
Wu,C.P.;Tarn,J.Q.;Chi,S.M.(1996b):An asymptotic theory for dynamic response of doubly curved laminated shells.International Journal of Solids and Structures,vol.33,pp.3813-3841.
Xie,G.Q.;Chi,M.X.(2014):Sensitivity of dynamic response of a simply sup-ported functionally graded magneto-electro-elastic plate to its elastic parameters.CMC-Computers,Materials,&Continua,vol.44,pp.123-140.
Zhong,Z.;Yu,T.(2006):Vibration of a simply supported functionally graded piezoelectric rectangular plate.Smart Materials and Structures,vol.15,pp.1404-1412.
Appendix A.The expressions of Kij
The relevant differential operatorsKij(i,j=1-3)andIkl(k=1,2;l=0-2)in Eqs.(42)-(44)are given as follows:
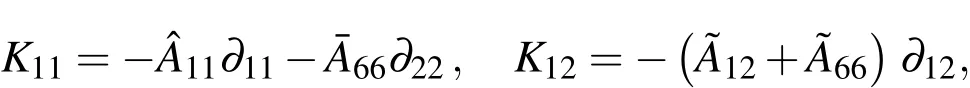
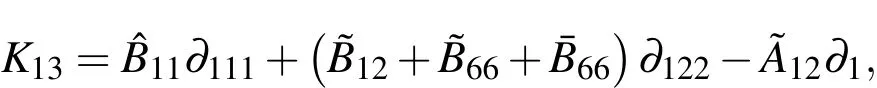

in which

Appendix B.The expressions ofkij(i,j=1−3)
The relevant differential operatorskij(i,j=1−3)in Eq.(69)are given as follows:
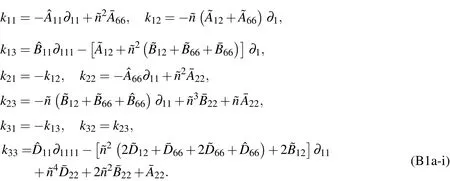
Appendix C.The expressions ofdij
The relevant differential operatorsdijin Eq.(70)-(72)are given as follows: