包含复合机构的6R机器人误差补偿算法与实验研究
2015-04-19田应仲聂杰聪张雯君
□ 田应仲 □ 聂杰聪 □ 张雯君 □ 李 龙
1.上海大学机电工程与自动化学院 上海 200072
2.上海大学上海市智能制造及机器人重点实验室 上海 200072
工业机器人精度是国内外研究的重要技术,是衡量其性能的重要指标之一,ISO 9283(工业机器人:性能标准和测量方法)描述了评价工业机器人精度的标准:重复定位精度、位姿精度以及轨迹精度[1]。其中,位姿精度和轨迹精度统称为绝对定位精度,它是机器人实际运动与期望运动之间的偏差。重复定位精度是机器人在重复执行同一期望运动时,其实际运动之间的相互离散程度。现阶段的工业机器人根据关节、构型、负载的不同,重复定位精度控制范围为±0.01~2 mm,绝对定位精度控制范围为±0.1~100 mm[2],即绝对定位精度远低于重复定位精度,难以满足工业发展的要求。因此,提高机器人绝对精度指标是目前急需解决的问题。目前机器人的标定方法通常分为运动学标定和非运动学标定,有研究结果表明,几乎95%的机器人定位误差是由自身运动学参数误差造成的。因此,采用基于运动学建模的方法,辨识出运动学参数并对机器人进行补偿,这将极大提高机器人的定位精度。
我国对机器人的误差补偿算法研究较晚,研究手段较少,目前,国内研究的误差补偿算法绝大多数是针对普通6R型工业机器人,而对包含复合机构的6R工业机器人的误差补偿算法研究极少。蔡鹤皋等[3]采用MDH模型推导出了具有通用性的串联机器人几何参数识别公式,并对RMA-I型机器人进行误差补偿后使其精度提高了一个数量级。南小海[4]利用MDH推导了Reis RV-16型串联机器人的实际几何参数识别公式,采用最小二乘法成功辨识出了运动学参数误差,补偿后大大地提高了机器人的位置精度。
笔者先推导机器人运动学误差模型及参数辨识方法,针对包含复合机构的川崎ZX165U型6R工业机器人,分析其机构特点及其MDH模型参数形式,利用高精度的激光跟踪仪为测量设备,采用改进的最小二乘法对参数进行辨识,利用辨识出来的参数修改机器人的运动学正解模型,从而达到误差补偿的目的,极大地提高了机器人的位置定位精度。
1 机器人运动学建模及参数辨识
根据经典的D-H模型,每个连杆可由4个参数(即扭角 αi-1,连杆长度 ai-1,连杆偏距 di和关节角 θi)来描述,但是,当相邻两关节轴线平行时,D-H模型违背了模型应具备连续性的准则,因为此时机器人几何尺寸的微小变化,会导致模型参数发生跳变,模型存在奇异性,导致无法辨识连杆参数。Hayati等[5]针对转动关节提出MDH模型,在原有的D-H模型上,引入附加转动项 Rot(y,βi)来避免奇异性,即建立 MDH 模型,该模型对应的齐次变换矩阵可表示为:
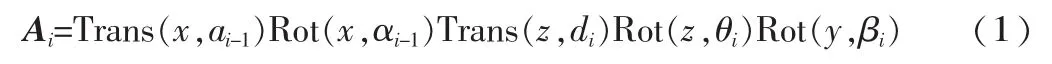
用矩阵表示为:

式中:s和c分别为sin和cos的缩写,当两相邻关节轴线 Zi-1与 Zi不平行时,βi=0。
对于n关节机器人,从机器人基座到末端执行器的坐标转换,即按照上述步骤依次进行坐标系的转换,将各个连杆的齐次变换矩阵依次相乘,得:

用P来表示机器人末端基于自身基坐标系的理论位置,则:

在机器人装配过程中会产生一些误差,如:进行机械校零时,由于角度编码器到达的零位无法与机器人的名义零位相一致,产生了零位误差Δθi;由加工和装配过程中而造成的长度误差Δdi和Δai;由机器人相邻的两轴线间存在平行度或者垂直度的误差而导致的角度误差Δαi和前面提到的Δβi,因此实际位置P′可表示为:

由于这些误差都比较小,可以简化为线性方程:

式(7)为机器人位置定位误差公式,可转化为:
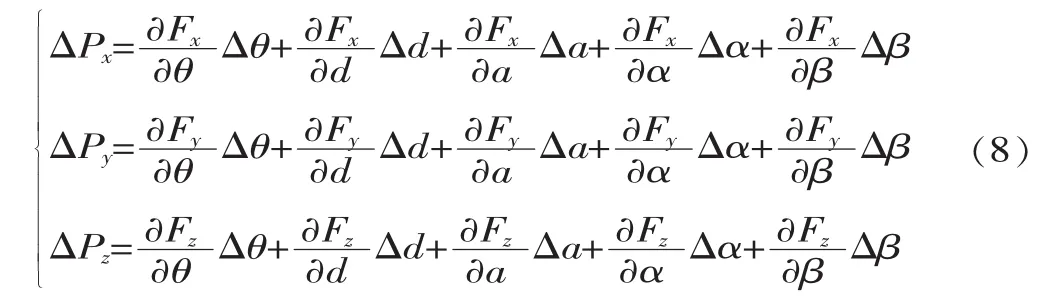
在式(8)中仅考虑位置误差,6关节机器人n个测量点的方程写成矩阵形式:

式(9)的正则方程为:

若[B]的列线性独立,则Δq的最小二乘解为:

式(14)中的Δq即为运动学参数的近似解,将求得的Δq值补偿到机器人的连杆参数上,得到新的连杆参数,再用新的连杆参数重新求解,多次迭代,直到ΔPx、ΔPy、ΔPz足够小,从而达到误差补偿、提高机器人定位精度的目的。
连杆参数误差补偿算法可以归纳为:①列出机器人的名义连杆参数;②根据名义参数和测量的数据,建立机器人运动学误差方程;③用最小二乘法解运动学误差方程,得到参数误差Δq;④根据得到的Δq,补偿连杆参数值;⑤转向②,直到 ΔPx、ΔPy、ΔPz都小于某一最小值;⑥连杆参数误差即为名义值与经过多次迭代最后所得的值之差。
2 误差补偿实例
目前,ABB、KUKA等大公司在码垛和搬运机器人中,大多采用抗冲击能力强的铰链式四连杆结构,该结构增加了整个臂部的刚度,为重型负载的设计要求提供了结构上的可行性。该四连杆结构具有行程放大功能,即以较小的驱动行程实现机器人末端较大的工作行程,从而可以满足码垛作业对大工作空间的性能要求[6]。川崎公司生产的ZX165U型机器人同样包含了铰链式四连杆结构(见2.1节介绍),笔者采用ZX165U型机器人为实例,对其进行误差补偿,验证上述补偿算法的有效性。
2.1 ZX165U型机器人简介
ZX165型机器人是一种大型通用工业机器人,该机器人在码垛时,能够保证整个末端(物体)平行移动而只需要最少的关节电机参与运作(JT2),节省资源,并且由于其底座阻尼器的作用,使整个运动过程速度稳定,更能保证物体的安全。图1所示的机器人的6个轴均是旋转轴,关节 1(JT1)、关节 4(JT4)、关节 5(JT5)和关节6(JT6)都是与一般的串联机器人相同的。而关节2(JT2)与关节3(JT3)之间在结构上是通过铰链式四连杆结构加上三角形结构来耦合的,正是因为使用了这种复合机构,使其能以低能耗实现手臂向后翻,就是因为此机构使它的运动规律与简单的串联机器人有所不同,也给D-H坐标系的建立和杆件参数的确定带来了困难。
把ZX165U型机器人简化成如图2所示结构简图,当机器人只有 JT2 运动时,连杆(3、4、5、6)始终作平移运动。
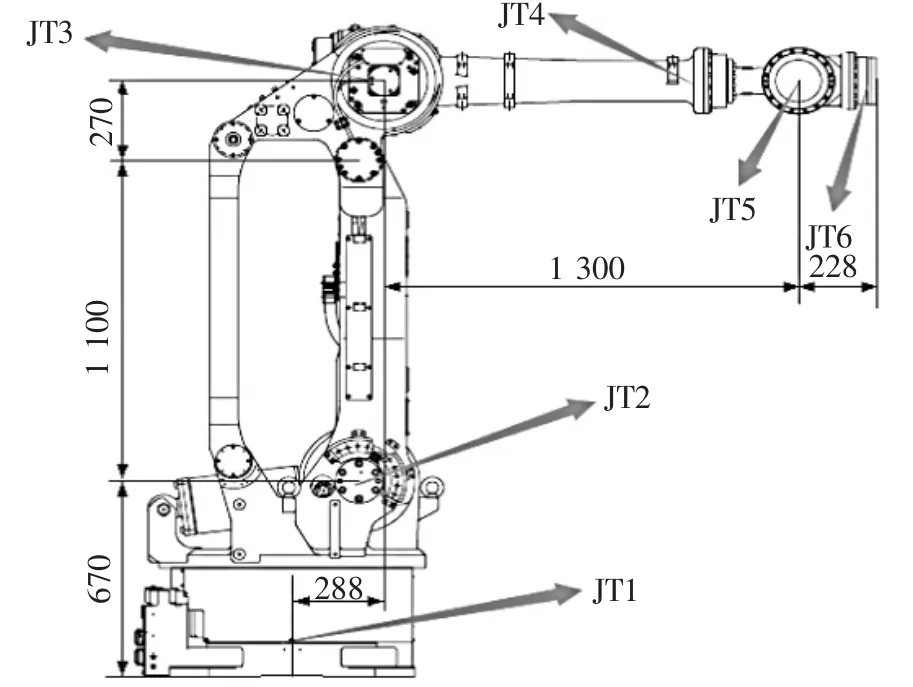
▲图1 ZX165U型机器人结构图
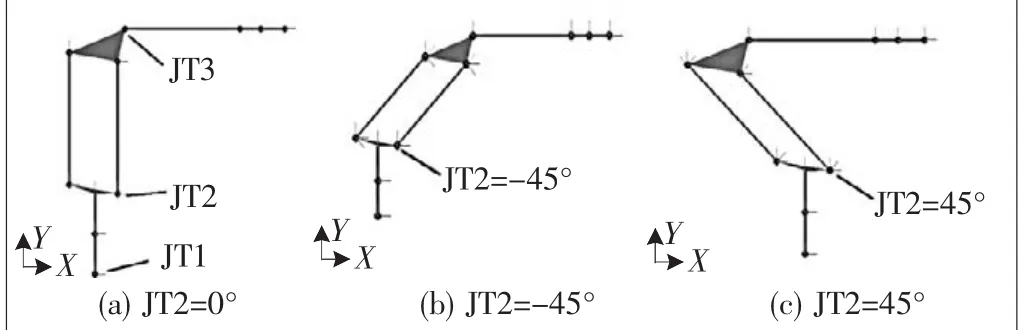
▲图2 当只有关节2运动时,机器人末端的运动状态

▲图3 混合铰链结构
将JT2和JT3处的平行四边形结构以及三角形结构的混合结构进行单独分析,如图3所示,可以确定JT3 的虚拟旋转中心为点 O, 得到∠C″BC′=∠E″OE′,∠CBC′=∠EOE′,得出虚拟中心O的转角与关节2的转角相等的结论,所以可用O点作为等效关节2。而连杆2的长度为OE的长度,即为CB的长度。另外,关节3处的转角因平行四边形关节有一个补偿,可知关节3转角为θ3+θ2。上述这些在之后建立的D-H坐标系以及D-H参数中都需考虑。
2.2 ZX165U型机器人运动学方程
根据2.1节对ZX165U型机器人进行分析,建立其连杆坐标系,如图4所示,可以看出,相邻关节轴线中只有JT2和JT3轴线在理论上相互平行,MDH名义连杆参数见表1。
由式(3)可知,末端法兰中心点相对于机器人基坐标系的转换矩阵为:

3 误差补偿实验及数据分析

表1 MDH名义连杆参数
本实验用Leica激光跟踪仪作为测量装备。首先,用激光跟踪仪构造机器人的基坐标系,步骤如下。
1)用示教器把机器人调整至初始位置 (JT1=-90°、JT2=-90°、JT3=0°、JT4=0°、JT5=0°、JT6=0°), 并将靶球放在机器人末端执行器上的某一固定点。
2)旋转轴1,其它轴的角度保持不变,每隔10°用激光跟踪仪测量机器人末端执行器上固定点的坐标值,根据这些坐标点拟合出一个圆1。
3)旋转轴2,其它轴的角度保持不变,每隔10°用激光跟踪仪测量机器人末端执行器上固定点的坐标值,根据这些坐标点拟合出一个平面2。
4)用激光跟踪仪测量基座所在的平面A。
5)根据圆1的法线和平面A的交点作为原点,平面2和平面A的交线作为Y轴,圆1的法线作为Z轴,根据右手定则定出X轴,结合激光跟踪仪自带软件,可建立ZX165U型机器人的虚拟基坐标系。
建立机器人的基坐标系之后,用激光跟踪仪在机器人包络空间内测量95个点,为避免误差补偿陷入局部最优,测量点均匀分布在整个工作空间,ZX165U型机器人需要辨识的模型参数共25个。采集完数据后,用其中34个点建立误差方程,按照前述方法用34个点来建立误差方程是充足的,其余61个点作为验证。
应用本文第1节的补偿算法,用MATLAB作为计算工具,得到MDH模型连杆参数误差,见表2。
利用表2得出的连杆参数误差对机器人名义连杆参数进行补偿,对用于建立误差方程的34个标定集补偿前后位置误差变化情况如图5所示,对用于验证结果的61个验证集补偿前后位置误差变化情况如图6所示。对位置误差进行数据整理,从表3可知,经过连杆参数误差补偿后,标定集位置误差均值从11.440 9 mm降到了0.237 8 mm,提高了97.92%,均方差从2.477 3 mm降到了0.157 4 mm,提高了93.65%;检验集位置误差均值从10.624 8 mm降到了0.368 7 mm,提高了96.53%,均方差从2.288 5 mm降到了0.204 6 mm,提高了91.06%,机器人误差补偿效果非常显著,说明了上述补偿算法的准确性。
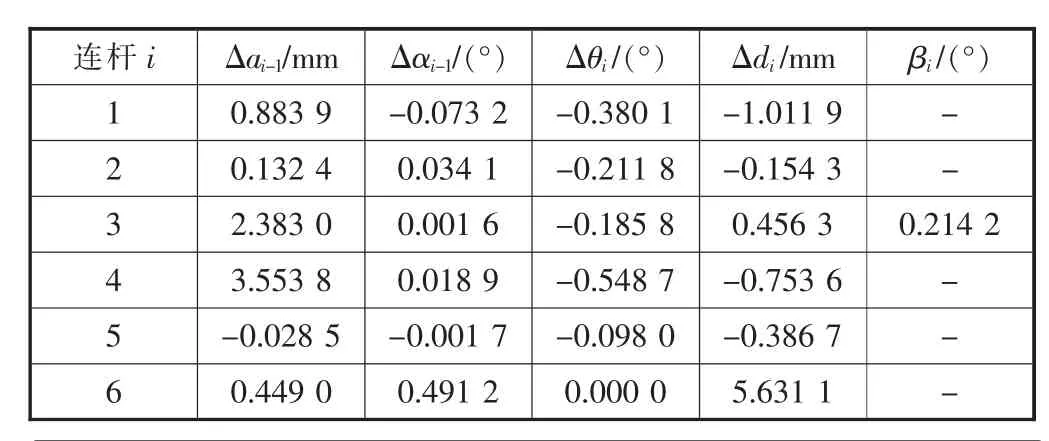
表2 MDH模型连杆参数误差

▲图4 ZX165U型机器人D-H模型
4 结论
提出了一种机器人位置误差补偿方法,首先对机器人进行运动学建模,并列出运动学误差方程,再通过最小二乘法辨识出所需的连杆参数,并予以补偿;此方法还考虑了相邻两关节间平行时引起的奇异性问题,并采用MDH方法消除其奇异性。以川崎公司生产的包含复合机构的ZX165U型机器人为实例,对其进行误差补偿,补偿后大大提高了机器人的绝对定位精度。
但机器人误差补偿是一项非常复杂的工作,笔者仅从运动学误差模型方面考虑提高其绝对位置定位精度,而对机器人杆件弹性变形、齿轮传动误差、关节间隙等因素尚未考虑进去,所以,要更进一步提高机器人的位置精度,还要依赖更完整的误差辨识模型。
[1]ISO 9283, Manipulating Industrial Robots-Performance Criteria and Related test Methods[S].
[2]Vatchara Lertpiriyasuwat.Real-time Estimation of Endeffector Position and Orientation for Manufacturing Robots[D].USA:Universtity of Washington, 2000.
[3]蔡鹤皋,张超群,吴伟国.机器人实际几何参数识别与仿真[J].中国机械工程, 1998, 9(10):11-14.

表3 标定集与检验集补偿前后数据分析

▲图5 标定集补偿前后位置误差对比
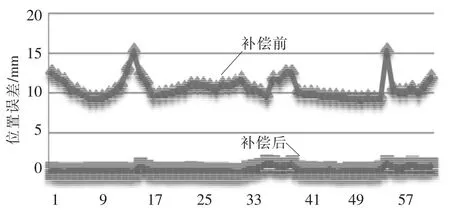
▲图6 检验集补偿前后位置误差对比
[4]南小海.6R型工业机器人标定算法与实验研究[D].武汉:华中科技大学,2008.
[5]HayatiS A.RobotArm GeometricalLink Parameter Estimation[C].Proeeedings of the 22nd IEEE Conference on Decision and Control,Pasadena,California,1983.
[6]李跃.重载码垛机器人机构设计及其运动控制研究[D].绵阳:西南科技大学,2013.
[7]任永杰,邾继贵,杨学友,等.利用激光跟踪仪对机器人进行标定的方法[J].机械工程学报,2007,43(9):195-200.
