基于衔接性协调的地铁换乘站候车客流优化
2015-04-19白广争石红国王秀玄
白广争,郭 进*,石红国,杨 扬,王秀玄
(西南交通大学a.信息科学与技术学院;b.交通运输与物流学院,成都611756)
基于衔接性协调的地铁换乘站候车客流优化
白广争a,郭 进*a,石红国b,杨 扬a,王秀玄a
(西南交通大学a.信息科学与技术学院;b.交通运输与物流学院,成都611756)
研究了高峰时段列车运行的衔接协调对换乘站候车客流量的优化问题.首先分析了换乘站各站台候车客流的组成因素,确定出各运行方向的换乘站台内客流量随时间变化的规律.然后,以时段内换乘站候车客流量的最大值最小为目标,建立优化模型.模型以站台最大可容纳候车人数为约束条件,以各方向列车在换乘站的到达时刻为调整对象,实现了高峰时段换乘站内聚集客流的优化.最后,针对验证案例,设计了遗传算法进行求解,得出了协调较优解,并给出与较劣解的对比分析.结果表明,该优化方法能够有效降低换乘站内的候车客流人数,可为网络化的优化协调工作提供参考.
城市交通;优化模型;遗传算法;换乘站;候车客流
1 引 言
城市轨道交通网络化运营对线路间列车的协调运行提出了迫切要求.这种协调性主要表现在两个方面:其一为线路间列车运行的衔接性协调[1-3],主要通过调整各线路列车在换乘站的到发时刻,使乘客在线路间的换乘等待时间最少,多应用于平峰或低峰时段;其二为线路间运力的协调[4,5],主要针对相交线路的行车间隔、列车编组或局部是否加开空车等,进行调整,以降低高峰时段换乘站的客流压力.
文献[3]分析了同台换乘情况下,两个运行方向上列车到达换乘站的时刻协调对站台内聚集客流的影响.文献[6]分析了普通车站站台内旅客的最高聚集人数的计算方法.而关于运行列车在换乘站的衔接性对站内候车客流量的影响研究相对较少.
本文在分析了换乘站内候车客流计算方法的基础上,以时段内换乘站中候车客流上限最小为优化目标建立模型.该模型能够在不额外增加开行成本的基础上,在一定程度内降低高峰时段换乘站内的客流压力,达到与采用运力调整方式相同的效果.
2 问题分析及基本假设
城市轨道交通网络是一个复杂的动态大系统.针对网络化的运营优化,首先应建立换乘站子系统所在衔接层的换乘优化模型,再从网络协调层对换乘节点间列车衔接方案进行全局递阶优化.本文主要对高峰时段换乘站子系统进行优化,讨论各方向列车的衔接性对站台聚集候车客流量的影响.
当车站建成后,站台大小是确定的,其能够容纳的最大候车人数也是有限的.站台内聚集客流量太大不但影响旅客的服务质量,而且直接关系到旅客的出行安全.因此,高峰时段换乘站的优化不但要提高换乘站的运作效率,而且要优化站内的聚集人数,使客流在换乘节点处尽量平缓流通,避免出现峰值过高的情况.
然而,站厅站台的大小、换乘方式的选择、换乘设施的能力等均会对旅客的换乘走行时间及换乘客流强度造成影响.例如:当换乘通道内客流大量聚集时,旅客站内换乘走行时间延长,时长分布更分散,且部分乘客可能会放弃换乘.这些因素均对换乘站内聚集客流的统计造成不利影响.为了降低问题复杂度,本文仅考虑各换乘站台内聚集的候车客流量,对于站内换乘走行过程及下车旅客的疏散过程所造成的站台客流变化影响暂不做考虑.
根据以上分析,高峰时段换乘站列车到站时刻协调的目标是使得该时段换乘站内最大聚集候车人数最小.即,在[Ta,Tb]高峰时段内,假设在tmax(tmax∈[Ta,Tb])处客流量聚集人数达到最大值,其对应候车客流量为PDmax,则,协调优化各方向列车到达换乘站时刻的目标是实现min{PDmax}.
本文讨论两条线路相交的情况.各方向上列车均衡行车,同一线路的上、下行之间旅客不产生换乘关系.同一换乘方向上,旅客在换乘站内的纯换乘时间各不相同,与旅客的年龄、出行目的及车站换乘设施的布置等均有关系,本文根据调研数据取均值[2].假设时段内站外到达换乘站任一线路运行方向站台的客流服从均匀分布[6],同一换乘方向上换乘客流随各趟列车均匀到站.根据以上假设,对于相交的两线路L1、L2,以L1上行换乘站台客流为对象进行分析,其他方向换乘站台的客流可同理得出.对所有换乘站台内客流求和,即可得出换乘站内总候车客流量,即优化主体.
图1给出L1上行站台内的候车客流模型.由图1,换乘站内L1上行站台客流量由4个因素决定,分别为站外进站搭乘L1上行列车的客流、L2上、下行分别带来的换乘L1上行的客流和L1上行列车运出换乘站的客流.
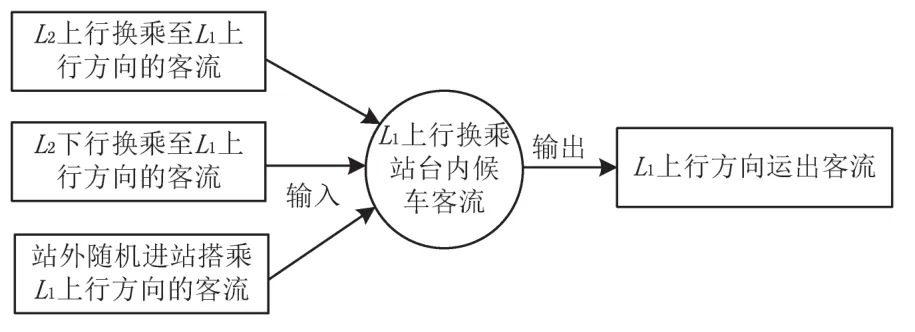
图1 线路L1上行换乘站台候车客流模型Fig.1 Model of the waiting passengers in l11platform
本文首先计算线路L1上行换乘站台内的候车客流量,在此基础上,建立换乘站候车客流优化模型,最后通过案例分析求解,得出结论.
3 符号变量说明
为了便于问题描述,对文中变量作如下统一说明:
lpq——线路Lp的q方向,其中q=1表示上行,q=2表示下行;
hp——线路Lp上、下行方向上列车的行车间隔;
μ——弹性时间,用于表示列车到站时刻波动;
Dp——线路Lp上、下行方向列车在换乘站的停站时间;
4 线路L1上行站台候车客流量计算
首先计算L1上行到达客流量,然后计算L1上行离去客流量,最后得出L1上行站台候车客流量.
4.1 线路L1上行到达客流量计算
线路L1上行的到达客流由站外随机到达客流和换乘到达客流组成,以下分别计算.
4.1.1 线路L1上行站外到达客流量计算
假设站外到达线路L1上行站台的客流平均到达速率为,则,对于开行时段内的任意时刻t(t∈N,单位:s),在(Ta,t)的时间段内,站外到达L1上行站台的客流量为

4.1.2 由L2换乘到L1上行的客流量计算
在(Ta,t)时间段内,自线路L2换乘至线路L1上行站台的客流由 l21→l11换乘客流和换乘客流组成.以下详细介绍的求解过程,可同理得出.
假设由L2上行第x趟到达列车实际换乘到L1上行的客流量为,则,(Ta,t)的时间段内,计算为

式中 μ表示弹性时间,用于解决列车运行时由于受到各种干扰,造成与图定到站时刻偏离的问题,据文献[7]研究,设μ服从正态分布,其均值为0,方差σ根据统计数据确定.

4.1.3 总到达客流量计算
根据以上分析,在(Ta,t)时间段内,到达线路L1上行站台的客流总量为
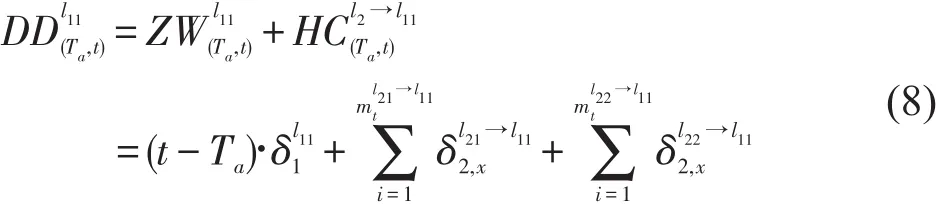
4.2 线路L1上行离去客流量计算
在(Ta,t)时间段内从线路L1的上行换乘站台离去的客流量,可通过对该运行方向上各趟离去列车所运走的客流量求和得到.
4.2.1 线路L1上行随第i趟列车离去的客流量计算
假设线路L1上行第x趟到达换乘站的列车在旅客下车后,能够提供的空位数为,到达换乘站的时刻为,对应离站时刻为.则,该趟车实际从换乘站运出的人数为

式中 n表示时段内L1上行共开行的列车对数;表示L1上行第x趟车离站前在l11站台候车人数,其公式为
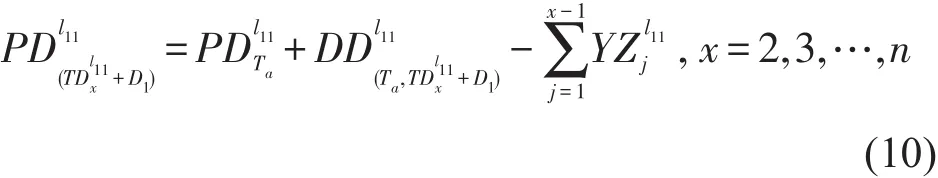
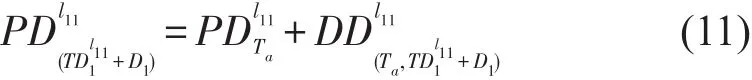

根据式(9)~式(12),可以递推出线路L1上行随第x趟列车离开换乘站的旅客人数.
4.2.2 (Ta,t)时间段内线路L1上行离去客流量计算
假设旅客乘上列车即被认为离开了换乘站,则,(Ta,t)时间段内线路L1上行离去客流量的计算分以下三种情况讨论.
即L1上行第一趟列车还没有到达.则,(Ta,t)时间段内L1上行线路上没有列车离开换乘站.则,离去客流为
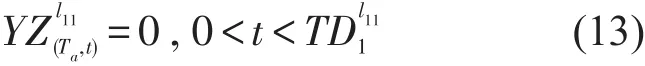
即时刻t分布在第x-1(2≤x≤n)趟车离去时刻与第x趟车到站时刻之间.则,根据4.2.1节的计算,对(Ta,t)时间段内线路L1上行随各趟列车离去的人数求和,即可得为
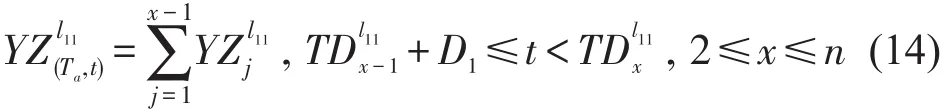
即时刻t分布在第x趟到达列车的停站时间段内.则,(Ta,t)时间段内线路L1上行离开换乘站的旅客总人数应在式(14)的基础上,增加的停站时间内的上车人数,则,为

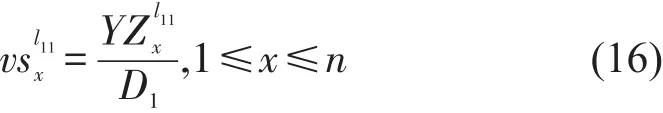
4.3 线路L1上行站台内候车客流量计算
根据4.1及4.2节的计算,开行时段内任意时刻t,L1站台内候车客流量值PDl11t为
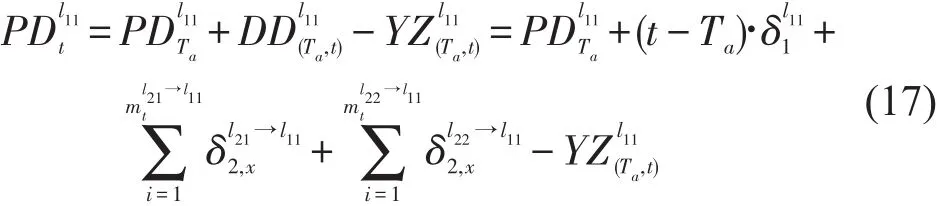
综合以上分析求解,可以得出在线路L1上行站台内候车旅客人数随时间t的变化规律.同理,可求得的表达式,不再详述.
5 换乘站候车客流优化模型
5.1 优化目标
在高峰时段,换乘站候车客流的优化目标为使时段内换乘站各站台的候车客流量总和的最大值最小,如式(18)所示.
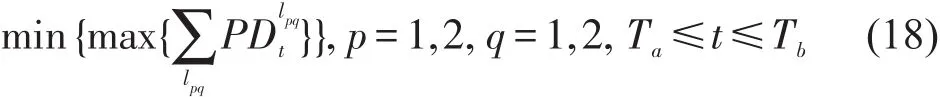
5.2 约束条件
假设各线路均采取岛式站台,则时段内各线路的换乘站台内,候车客流量的最大值应小于该换乘站台的最大可容纳人数,其公式为


根据第4节及本节建立的优化模型,可在确定的行车间隔下,实现两线路列车在换乘站的到达时刻协调优化.
6 案例与求解
以某城市两相交线路为例,如图2所示,验证所建优化模型的有效性.
图2 线路相交图Fig.2 Two lines intersection diagram
图2中两条线路相交于a换乘站.取早高峰7:00~8:00作为研究时段,设置初始数据如表1~表3所示.

表1 基础数据Table 1 Basic data

表2 各运行方向客流参数取值Table 2 Parameters of passengers in each direction
表3 换乘客流数据(人)Table 3 Parameters of transfer passengers
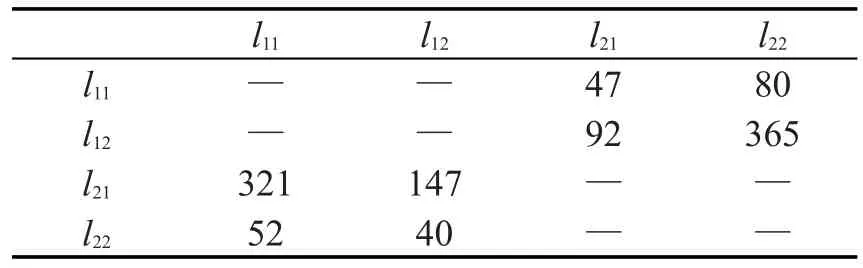
表3 换乘客流数据(人)Table 3 Parameters of transfer passengers
l11l12l21l22l11 l12 l21 l22————47 9280 365 321 52 147 40————
6.1 算法设计
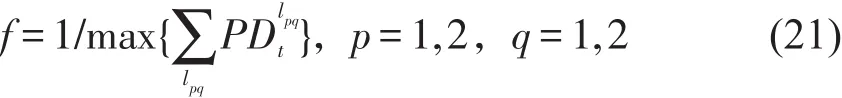
为了体现出优化效果,将适应度函数修改为式(22),其他参数不变,即可求得模型的较劣解.

6.2 计算结果及分析
根据所建立的模型及设计的算法进行求解,以下分别列出模型的优化解和较劣解,并对两类结果作对比分析.
6.2.1 优化解
经过计算,以7:00作为初始时刻0,表4列出了4组优化的各方向列车初始到站时刻解及对应的换乘站高峰时段内最大的聚集人数.需要指出的是表中所列数据并不代表全部优化解.

表4 部分协调优化解Table 4 Optimal solutions
以表4中第1组到站时刻数据为例进行协调,各方向初始列车到达换乘站的时刻分别为,L1上行7:00:15,下行7:01:54,L2上行7:02:41,下行7:00:33,以后各趟列车的到达时刻为在此基础上依次增加本线路整数个行车间隔,则7:00~8:00时段内,换乘站内候车客流的最大值为1 002.计算的各候车客流参数变化如图3所示.

图3 优化解对应换乘站候车客流变化规律Fig.3 Variation for number of waiting passengers in transfer station for optimal solutions
图3中,换乘站内候车客流总量变化幅度较小,到达客流能够快速被疏散,避免了换乘客流叠加现象,实现了优化换乘站内客流聚集量的目标.
6.2.2 较劣解
将适应度函数值设置为式(22)的形式,其他参数均不变,则可计算出衔接性协调较差的解.表5列出了衔接协调较差情况下,各方向列车初始到站时刻及对应换乘站内的最大聚集人数.
以表5中第1组数据为例,若各方向初始列车到达换乘站的时刻为:L1上行7:02:04,下行7:02:09,L2上行7:01:27,下行7:01:29,以后各趟列车的到达时刻为在此基础上依次增加本线路整数个行车间隔,则7:00~8:00时段内,换乘站内候车客流的最大值为1 402.各换乘站台候车客流及站内总候车人数变化如图4所示.

表5 部分协调较劣解Table 5 Bad solutions

图4 较劣解对应换乘站候车客流变化规律Fig.4 Variation for number of waiting passengers in transfer station for bad solutions
图4显示,由于各方向衔接协调较差,造成换乘站内最大聚集客流量非常大,且与图3相比,客流流通缓慢,滞留现象严重.因此,这种列车到站衔接方式应该尽量避免.
6.2.3 结果分析
对比表4、表5及图3、图4,在保持各线路运力不变的情况下,换乘站不同的衔接方案会对站内的候车客流量造成一定的影响.根据表4、表5中所列数据,优化解对应的换乘站候车客流上限值与较劣解对应参数相比,约缩减了27.7%.
由于模型中引入了弹性时间μ,考虑了列车在运行过程中可能受到的干扰问题,因此,最终求解结果具有较强的鲁棒性.
7 研究结论
本文分析了换乘站内候车客流的计算方法,研究了高峰时段线路间衔接性协调优化问题,建立了优化模型.通过案例分析,验证了线路间合理的衔接性协调能够有效缓解高峰时段换乘站内的候车客流量.根据文中得出的列车到站时刻,及列车在线路各区间的运行时间和停站时间,可反推出列车在始发站的发车时刻.本文研究过程中对旅客站内换乘走行时间等参数做了简化处理,在后续工作中将对模型做进一步的优化.
[1]Rachel C W Wong,et al.Optimizing timetable synchronization for rail mass transit[J].Transportation Science.2008,42(1):57-69.
[2]周艳芳,周磊山,乐逸祥.城市轨道网络换乘站列车衔接同步协调优化研究[J].铁道学报.2011,33(3): 9-16.[ZHOU Y F,ZHOU L S,YUE Y X.Synchronized and coordinated train connection optimization for transfer stations of urban rail networks[J].Journal of the China Railway Society.2011,33(3):9-16.]
[3]王菲,孙全欣,毛保华,等.基于时刻表协调的同台换乘聚集人数计算模型[J].交通运输系统工程与信息. 2013,13(3):163-169.[WANG F,SUN Q X,MAO B H, et al.Calculation model for passenger assembling on one-platform-transfer station based on timetable coordination[J].Journal of Transportation Systems Engineering and Information Technology,2013,13(3): 163-169.]
[4]王婵婵,刘加华,朱霞.不同行车密度下轨道交通换乘站客流情况研究[J].城市轨道交通研究.2011(6):37-39.[WANG C C,LIU J H,ZHU X.Passenger flow at rail transit station transfer in different rates of traffic flow[J].Urban Mass Transit Research.2011(6):37-39.]
[5]汪波,韩宝明,牛丰,等.城市轨道交通网络运力优化配置研究[J].铁道学报.2011,33(12):9-14.[WANG B,HAN B M,NIU F,et al.Study on optimization of transport capacity allocation for urban mass transit network[J].Journal of the China Railway Society.2011, 33(12):9-14.]
[6]赵宇刚,毛保华,杨远舟,等.城市轨道交通站台最高聚集人数计算方法研究[J].交通运输系统工程与信息.2011,11(2):149~154.[ZHAO Y G,MAO B H, YANG Y Z,et al.Methods of calculating the maximum assembling on urban rail transit platforms[J].Journal of Transportation Systems Engineering and Information Technology.2011,11(2):149-154.]
[7]赵宇刚,毛保华,蒋玉坤.基于列车运行时间偏离的地铁列车运行图缓冲时间研究[J].中国铁道科学,2011,32(1):118-121.[ZHAO Y G,MAO B H,JIANG Y K. Study on buffer time of metro train diagram based on train running time deviation[J].China Railway Science, 2011,31(1):118-121.]
Optimization for Waiting Passengers in Transfer Station Based on Train Connecting Coordination
BAI Guang-zhenga,GUO Jina,SHI Hong-guob,YANG Yanga,WANG Xiu-xuana
(a.School of Information Science and Technology;b.School of Transportation and Logistics, Southwest Jiaotong University,Chengdu 611756,China)
Optimization for the number of waiting passengers in transfer station by coordinating trains’arriving time in the rush hour is studied.Firstly,it analyzes each factor which had influence on the passengers in each platform,and obtains formulas to describe the variation of waiting passengers with time in each direction.Secondly,it establishes the optimization model which minimizes the maximum of total waiting passengers during the study period.The model takes the site capacity as constraints,and takes trains’arrival time in each direction in transfer station as adjustment object.Finally,the model is validated by an example,and genetic algorithm is designed to search the optimal solutions.It also obtains some worse solutions for contrast.By contrast,the optimal solutions can effectively reduce the number of waiting passengers in transfer station.The study can provide a reference for network coordination.
urban traffic;optimization model;genetic algorithm;transfer station;number of waiting passengers
1009-6744(2015)01-0191-07
:U292.4+1
:A
2014-07-25
:2014-10-29录用日期:2014-11-13
国家自然科学基金(U1334201);中国铁路总公司重大课题(2013X012-A-1,2013X012-A-2,2014X008-A).
白广争(1986-),男,山东曹县人,博士生. *
:jguo_scce@home.swjtu.edu.cn
