路网应急疏散理想与保守疏散时间流研究
2015-04-19严余松
马 毅,严余松
(1.西南交通大学 交通运输与物流学院,成都610031;2.四川师范大学 计算机科学学院,成都610068)
路网应急疏散理想与保守疏散时间流研究
马 毅1,严余松*2
(1.西南交通大学 交通运输与物流学院,成都610031;2.四川师范大学 计算机科学学院,成都610068)
研究应急疏散问题的理想疏散时间流及保守疏散时间流对于估计真实突发事件下的疏散时间具有重要的指导意义.为此构建了理想疏散时间流与保守疏散时间流问题的数学规划模型,并借鉴经典网络流理论的最短路、最长路、最小费用流算法原理,设计了求解理想疏散时间流与保守疏散时间流的两个增广路算法.该算法不但可以求得理想疏散情况及最坏疏散情况下的流量分布,还可以计算出各自对应的理想疏散时间和保守疏散时间,从而识别出应急疏散总时间的范围域.最后通过算例演示了理想疏散时间流及保守疏散时间流的求解过程,并讨论了他们的变化特征.
交通工程;应急疏散时间;时间流算法;理想疏散时间;保守疏散时间;最小费用流
1 引 言
近段时间,由于国内各大城市突发性事件频繁发生,使得路网应急疏散问题再次成为研究人员关注的热点.路网应急疏散问题是指当城市发生突发性事件时,将处于事件发生地点的受危人群通过路网中的各条道路疏散至安全地点,从而将突发性事件带来的影响尽量降到最低.
与微观尺度的应急疏散研究相比[1-3],路网尺度的应急疏散研究更适合计算突发事件下疏散流量、密度、速度等重要的统计量,且开展起来相对容易.目前,有关路网尺度的应急疏散研究,Cova[4]提出了一个在复杂路网中识别最优的基于车道的疏散路径规划模型,该模型在本质上是一个最小费用流模型.Tjandra等人[5]用一种动态网络流模型描述了疏散问题,并建立了最快速流模型,同时设计了求解该模型的单源点算法.Campos等人[6]基于最短路算法,以路径集内总通行能力与旅行时间比值最大化为目标,求得了核电站事故地点至受灾人员接收地点的k条独立的疏散路线.Hamacher等人[7]对路网应急疏散问题进行了综述研究,探讨了路网应急疏散问题的最大流、最快速流等多个数学模型.Brachman等人[8]将基于地理信息系统的引导技术应用于路网疏散研究中,建立了相应的最快速模型,并用实例验证了引导技术对疏散最快速流带来的积极作用.国内虽然对路网应急疏散的研究起步较晚,但同样取得了丰富的研究成果,高明霞等[9]建立了考虑交叉口延误和通行能力的最小费用流模型来描述城市内车辆的疏散路线问题,并设计了一个最小费用路算法来对模型进行求解.袁媛等人[10]考虑了灾害扩散的实时影响,将疏散路网中各路段上的疏散速度表示为随时间变化的连续递减函数,并建立了对应的疏散路径选择模型.宁宣熙[11]建立了考虑拥堵的情况下,基于预估时间增量比较算法的疏散路径的最短时间流路径选择模型,该模型充分考虑了流量变化对疏散时间的影响.
综上所述,现有关于路网应急疏散的研究,其建模及求解思想基本上都是在经典最小费用流问题基础上衍生而来的,但实际上疏散所需的总时间并不是“时间费用”的总和,而是其中受危人员通过时间最长的可行路径时所需要的通过时间,也就是说,用“最小费用流”来表达最短疏散时间是有限制的.此外,现有大部分研究只考虑了理想情况下的最短疏散时间情况,但在某些情况下,我们需要知道将全体受危人员疏散完毕所需要的最长疏散时间,即保守疏散时间.一方面用以明确疏散过程的时间范围,另外也可为制定疏散引导措施提供一定的理论支撑.
鉴于此,本文通过研究理想疏散情况下的最短疏散时间流与最坏疏散情况下的保守疏散时间流,并设计算法来求解对应的流量分布及疏散时间,以此来达到明确应急疏散时间范围,合理制定疏散方案的目的.
2 路网应急疏散的理想疏散时间流与保守疏散时间流问题
2.1 问题的提出
疏散路网可以用图论的方法来表示,现将疏散路网记为G(V,A,C,T).其中V表示路网G的节点集;A={(vi,vj)|vi,vj∈V}为弧集,代表各节点之间的道路;C={cij|(vi,vj)∈A}为容量集;T={tij|(vi,vj)∈A}为时间集,tij表示流 fij通过弧(vi,vj)时所需要的通过时间,因各条道路上的通行条件各异,使得各弧(vi,vj)上的通过时间tij不尽相同.针对该疏散网络G,则疏散过程可表示为将位于紧急事件发生地点vs的受危人员疏散到安全地点vt.
路网应急疏散问题具有以下基本定义及基本定理[11]:
定义1(疏散基本路) 疏散基本路Pk是指疏散路网中任意一条由事故发生地点至安全地点的可行通路.
定义2(单位基本流) 单位基本流是指沿任意疏散基本路上的单位流动,即单位逃生者在任意基本路上的流动.
定义3(基本路的通过时间) 指基本流通过该基本路所需要的通过时间总和,表达式为

在疏散过程中,同一基本路通行时间的动态变化不容忽视,因为随着受危人员在路段上的不断聚集,造成通行时间受聚集人数的影响越来越显著,一般情况下,路段聚集人数对通行时间的影响呈如下函数关系:

定理1(疏散流的分解定理) 若疏散流 f是无环流,则它可由基本流线性表示为

式中 ξi(i=1,2,…,m)是 m条单位基本流;αi(i=1,2,…,m)为各单位基本流的量级.
定义4(疏散流的通过时间) 假设疏散流 f可由m条基本流组成,则该疏散流通过网络的所需时间并不是各条基本流通过时间的总和,而是其中通过时间最长的基本流的通过时间,即

定义5(理想疏散时间) 理想疏散情况下,将待疏散量疏散完毕所需要的最少通过时间.
定义6(保守疏散时间) 最坏疏散情况下,将待疏散量疏散完毕所需要的最少通过时间.
现以图1中的简单疏散网络为例,说明理想疏散时间与保守疏散时间的概念,路段旁边的数字分别表示该路段的通行时间和通行能力.
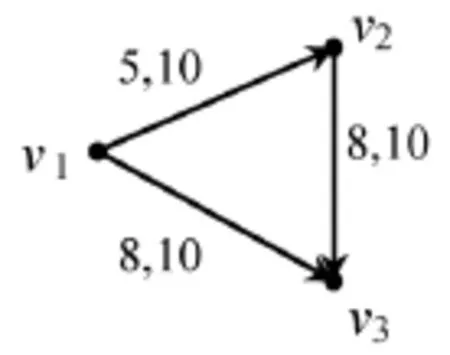
图1 疏散示例网络Fig.1 Demonstration network for evacuation
要将受危人员由事故地点v1疏散至避难地点v3.考虑到紧急事件造成的恐慌,造成人群在逃生过程中往往会随机地选择逃生路线,即路径的选择具有随机性,这种随机性就有可能造成两种极端的疏散情况:(1)理想情况,受危人员随机选择了时间最短路径v1→v3作为逃生路线,总的疏散时间为8,即理想疏散时间;(2)最坏情况,受危人员随机选择了时间最长路径v1→v2→v3作为逃生路径,总的疏散时间为13,即保守疏散时间.
2.2 路网应急疏散理想疏散时间流与保守疏散时间流的数学模型
根据以上定义,设待疏散流量为q,用xij表示疏散过程中弧(vi,vj)上的流量,则可将应急疏散的最短时间流问题归纳为下面的数学规划模型:
(1)理想疏散时间流目标函数.

(2)保守疏散时间流目标函数.

约束条件如下:
(1)容量限制条件.对G中每条弧(vi,vj),有

(2)平衡条件.
对于起点vs,满足
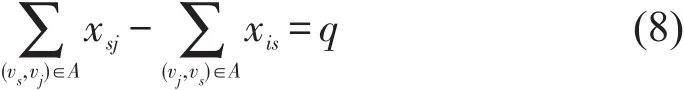
对于终点vt,满足
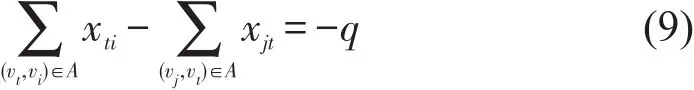
对于中间节点,流入量应等于流出量,即对每个vi(vi≠vs,vt)

3 理想疏散时间流的求解算法
众所周知,经典网络流理论中的最小费用流算法是解决含权网络流问题最有效的算法之一,如果把最小费用流问题中的弧权由“费用”改为“时间”,那么只需要对最小费用路算法作适当的修正,即在流量加载过程中,每次均以单位基本流为流量加载单元加载于路网,更新路段通行时间,直到加载完全部疏散流量q,即可求解出理想情况下的最短疏散时间流,最后一次流量加载时,相应加载路径的通行时间即为理想疏散时间,现给出该算法的基本步骤.
设待疏散量为q,用k表示流量加载的次数.
第0步 置k=0,并设初始流量为 f(k)=0.
第1步 构造当前流 f(k)的增量网络N(f(k)),其构造方法同最小费用流算法.
第2步 在增量网络N(f(k))中搜索通行时间最短的增广路,可应用Ford算法进行搜索,如果增量网络不存在增广路径则算法停止.否则,在该时间最短路上加载一个单位的基本流(注:正向弧增加,反向弧减少),并更新流量 f(k+1)=f(k)+1.
如果流量 f(k+1)的流值等于q,算法停止,表示人群疏散完毕;否则,利用式(2)更新各条路段的通行时间,置k=k+1,转第1步.
4 保守疏散时间流的近似求解算法
应急疏散的最坏情形是受危人员随机选择了时间最长路径作为逃生路线,因此求解保守最短疏散时间流的关键是搜索时间最长路,但是,一般网络图的最长路径问题是NP-Hard问题,不存在有效的多项式算法,而如果是有向无环图,则可以通过改进Dijkstra算法进行求解.现借鉴Dijkstra算法的递推原理,给出一种基于Dijkstra算法的变种算法来搜索时间最长路,其基本步骤如下.
对于有向无环网络,将节点分为两种类型:P标号点和T标号点,P标号标注已经正确得到最长路的点;T标号标注未得到最长路的点,T标号值表示最长路的下限,弧(vi,vj)的长度为wij.
第0步 令P(vs)=0,T(vi)=0,i=1,2,…t.
第1步 更新T标号值,假定vi是新产生的P标号,对vi指向的节点vj,进行如下修改:

式中 右边的T(vj)表示vj点旧的T标号值.
第2步 产生新的P标号点,其方法是:将P标号点vi所关联的边都删掉后,将入度为0的点标记为新的P标号点.
重复上述步骤直至终点由T标号变为P标号,回溯即可找出起点到终点的最长路.
基于上述最长路径搜索方法,将经典网络流理论中的最小费用流算法加以改造,即可用于求解近似保守最短疏散时间流.其基本步骤如下所示,并且在流量加载完毕后,重新搜索整个网络的时间最长路,该最长路即为保守疏散时间.设待疏散量为q,用k表示流量加载的次数.
第0步 置k=0,并设初始流量为 f(k)=0.
第1步 构造当前流 f(k)的增量网络N(f(k)),其构造方法类似于最小费用流算法,但不同之处在于,当弧上实时流量时,并不构造与原弧方向相反的“时间费用”为的反向弧,这样做的目的是避免在增量网络中寻找时间最长路径时出现回路,造成无法找到有效的最长路径;当弧上实时流量时,将该弧冻结,设置为无效路径.
第2步 在增量网络N(f(k))中用上述Dijkstra变种算法搜索通行时间最长的增广路,如果增量网络不存在增广路径则算法停止.否则,在该增广路上加载一个单位的基本流并更新流量.
如果流量 f(k+1)的流值等于q,算法停止,表示人群疏散完毕;否则,利用式(2)更新各条路段的通行时间,置k=k+1,转第1步.
5 计算示例
下面通过一个算例来说明理想疏散时间与保守疏散时间之间的关系.示例路网如图2所示,弧旁的数字分别表示路段零流下的通行时间和通行能力,节点v1为事故地点,节点v9为安全地点.现应用本文设计的算法,计算不同受危人数输入情况下的理想疏散时间与保守疏散时间.疏散人数设置为1到900,取路段拥挤参数α=1,β=1,计算结果如图3所示.
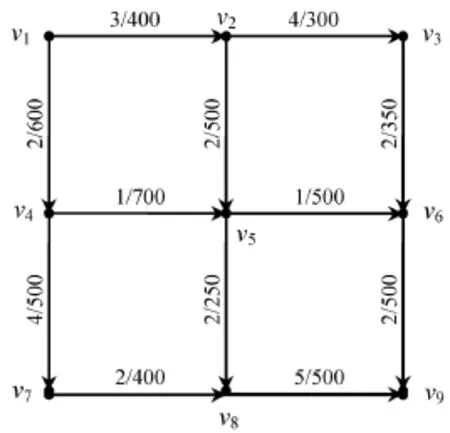
图2 示例网络Fig.2 Demonstration network
图3表明了该应急疏散网络在疏散人数不大于900的情况下,疏散时间的范围域,即理想疏散时间曲线与保守疏散时间曲线之间的区域.其中,理想疏散时间曲线代表了疏散时间的理论下限,即全体受危人员最快可以在该理论下限时间内疏散完毕;保守疏散时间曲线代表了疏散时间的理论上限,即在受危人员在网络中不作停留的情况下,必可在该该时间理论上限内疏散完毕.
而对于理想疏散时间与保守疏散时间随不同疏散人数的变化趋势,由图3表明,随着疏散人数的不断增加,二者的差值呈现先增加再减少的趋势,并在末尾处近乎相等.这是由于随着疏散人数的不断增多,路网的拥挤效应越来越明显,这也会使得理想疏散时间变得越来越不“理想”.
表1列出了当疏散人数设定为900时的理想疏散流量分布情况与保守疏散流量分布情况,此时对应的理想疏散时间为23.72,即受危人群最短可以在23.72个单位时间内到达安全地点;对应的保守疏散时间为24.87,即受危人群到达安全地点的最长时间不会超过24.87个单位时间.

图3 不同疏散人数下理想疏散时间与保守疏散时间Fig.3 The ideal and conservative evacuation time by different evacuee numbers

表1 理想及保守疏散情况下的流量分布情况(疏散人数设定为900)Table 1 Distribution in ideal and conservative evacuation situation(input numbers:900)
6 研究结论
(1)探讨了路网应急疏散理想疏散时间流问题与保守疏散时间流问题.理想疏散时间流和保守疏散时间流是应急疏散时受危人群流动分布的两种极端状态.求解理想疏散时间流与保守疏散时间流,可以明确疏散过程的时间范围,也能够在一定程度上揭示哪些路径是疏散时的关键路径,哪些是不合理路径,从而为制定合理的应急疏散方案提供必要的理论依据.
(2)设计了求解理想疏散时间流问题与保守疏散时间流的网络增流算法.通过该算法,不但可以求解得到理想疏散情况及最坏疏散情况下的流量分布,还可以计算出分别对应的理想疏散时间和保守疏散时间,为研究应急疏散时疏散时间问题提供了一种重要的工具.
[1]Chen C K,Li J,Zhang D.Study on evacuation behaviors at a T-shaped intersection by a force-driving cellular automata model[J].Physica A:Statistical Mechanics and its Applications,2012,391(7):2408-2420.
[2]Zheng Y,Jia B,Li X G,et al.Evacuation dynamics with fire spreading based on cellular automaton[J].Physica A:Statistical Mechanics and its Applications,2011,390 (18):3147-3156.
[3]Wang L,Liu M,Meng B.Incorporating topography in a cellular automata model to simulate residentsevacuation in a mountain area in China[J].Physica A: Statistical Mechanics and its Applications,2013,392 (3):520-528.
[4]T J Cova,J P Johnson.A network flow model for lanebased evacuation routing[J].Transportation Research Part A:Policy and Practice,2003,37(7):579-604.
[5]Stevanus A,Tjandra.Earliest arrival flow with time dependent capacity approach to the evacuation problems[C].Pedestrian and Evacuation Dynamics 2002,Berlin,Springer press,2002:267-276.
[6]Campos V B G,da Silva.Evacuation transportation planning:A method of identifying optimal independent routes[C]//Proceedings of Urban Transport V:Urban Transport and the Environment for the 21st Century, Southampton,WIT press,2000:555-564.
[7]H W Hamacher,S A Tjandra.Mathematical modelling of evacuation problems:A state of art[C].Pedestrian and Evacuation Dynamics 2002,Berlin,Springer press, 2002:227-266.
[8]Brachman M L,Dragicevic S.A spatially explicit network science model for emergency evacuations in an urban context[J].Computers,Environment and Urban Systems,2014,312(44):15-26.
[9]高明霞,贺国光.考虑交叉口延误和通行能力优化疏散救援路线的最小费用流模型[J].系统工程,2006,24(9):6-10.[GAO M X,HE G G.Using minimum cost flow model to optimize evacuation routes considering delays and capacity at intersections[J]. Systems Engineering,2006,24(9):6-10.]
[10]袁媛,汪定伟.灾害扩散实时影响下的应急疏散路径选择模型[J].系统仿真学报,2008,20(6):1563-1566. [YUAN Y,WANG D W.Route selection model in emergency evacuation under real time effect of disaster extension[J].Journal of System Simulation,2008,20(6): 1563-1566.]
[11]宁宣熙.阻塞流理论及其应用(第二版)[M].北京:科学出版社,2009.[NING X X.Blocking flow theory and its application(the second edition)[M].Beijing:Science press,2009.]
Research on Ideal and Conservative Time Flow for Emergency Evacuation on Road Network
MAYi1,YAN Yu-song2
(1.School of Transportation and Logistics,Southwest Jiaotong University,Chengdu 610031,China;2.School of Computer Science,Sichuan Normal University,Chengdu 610068,China)
Studying ideal evacuation time flow and conservative evacuation time flow for emergency evacuation problem is significant to predict the evacuation time in the situation of emergency.In view of this objective,a mathematical programming model for ideal and conservative time flow is built,meanwhile,two flow-augmenting algorithm to solve this model is developed by means of theory of the shortest path,the longest path and the minimum profit flow,the algorithm can not only calculate the flow assignment in ideal and worst evacuation situation,but also can calculate the corresponding value of evacuation time respectively,further,identify the range of total evacuation time.Finally a demonstration example is used to demonstrate the calculation process of ideal and conservative time flow,as well as discussing its evolution properties.
traffic engineering;emergency evacuation time;time flow algorithm;ideal evacuation time; conservative evacuation time;minimum profit flow
1009-6744(2015)01-0167-06
:U491;O157.6
:A
2014-06-30
:2014-12-16录用日期:2014-12-22
国家自然科学基金(61104175).
马毅(1986-),男,重庆合川人,博士生. *
:414580215@qq.com
