互通立交匝道运行速度预测模型
2015-04-19张智勇郝晓云吴文斌
张智勇,郝晓云,吴文斌,王 东
(北京工业大学 a.北京市城市交通运行保障工程技术研究中心;b.交通工程北京市重点实验室,北京100124)
互通立交匝道运行速度预测模型
张智勇*a,郝晓云b,吴文斌b,王 东b
(北京工业大学 a.北京市城市交通运行保障工程技术研究中心;b.交通工程北京市重点实验室,北京100124)
匝道是互通立交的重要组成部分,基于运行速度的匝道设计理念是目前公路及互通立交一种新的设计思路.本文以互通立交匝道小型车辆的运行速度为主要研究目标,通过分析互通立交匝道运行速度的影响因素,制订正交实验方案,运用车载高精度GPS设备,采集了北京市4座互通式立交共14条匝道车辆连续运行速度数据.根据其中10条匝道的数据,按照车辆在互通立交匝道上的运行速度特性将匝道分为三段:减速段、匀速段、加速段,构建互通立交匝道各个分段运行速度与影响因素之间的预测模型,并使用另外4条匝道的实测数据对预测模型进行验证.结果表明,模型预测值的相对误差在5%以内,验证了模型的正确性.
交通工程;运行速度;互通立交;匝道;正交实验;预测模型
1 引 言
互通立交区运行速度特征是路线设计指标选用的基本依据,决定着立交的建设规模与安全水平.《公路路线设计规范》(JTG D20-2006)在总则中引入了运行速度与安全性评价的相关规定:“速度不同的设计路段相衔接处,或因条件制约线形设计受限制的地段,采用运行速度进行检验[1].”车辆运行速度预测模型是基于运行速度的线形设计方法的核心,是进行公路路线设计质量评价的前提和基础.国内外对此都进行了一定的研究和探索,上世纪70年代,欧美一些国家开始对运行速度预测模型进行研究,各国针对本国的实际情况开始不同道路条件下的运行速度观测与建模工作,并将研究成果应用于设计实践中.我国关于公路运行速度的观测与建模工作,在最近几年也进行了探索性研究,并取得了初步的应用成果,在一些设计和安全性评价中得到初步的验证和应用.高速公路互通立交匝道运行速度预测模型,目前国内外研究较少,因此,有必要选取不同类型的互通立交形式,有针对性的展开实地数据观测和调查,根据匝道运行速度特性,构建车辆在互通立交匝道不同组成部分的运行速度预测模型,确保互通设计类型和设计指标能够满足车辆连续、安全的运行要求,并保证互通区与衔接路段运行速度之间的协调性.
2 互通立交匝道的组成及运行速度的定义
2.1 互通立交匝道定义与组成
互通立交匝道[2]是用以联结上、下两条相交道路的左右转弯车辆行驶的道路.
匝道由以下三部分组成[3],具体如图1所示.
(1)驶出高速公路主要道路的减速车道;
(2)匝道路线;
(3)汇入高速公路主要道路的加速车道.
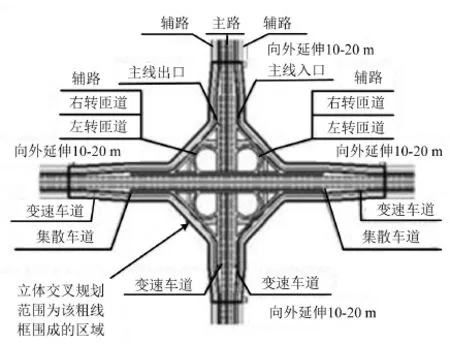
图1 互通立交组成部分示意图Fig.1 Interchange part
2.2 运行速度定义
公路线形设计,国际上一般采用两种不同的方法,即设计车速法和运行车速法.由于运行车速法与传统的设计车速法相比较有明显的安全效益,因而运行车速概念被澳大利亚、奥地利、法国、德国、希腊、波兰、瑞典、瑞士和英国等国家广泛应用.
基于运行速度、行驶速度、设计速度、限速、可能速度、期望速度之间的本质区别,以及国内外目前对运行速度定义的研究,本文定义运行速度是指当天气良好时,在潮湿、干净的路面上,且交通处于自由流状态时,在特定地点观测的车辆实际行驶速度,经统计分析,其分布曲线上的85%上对应的车辆行驶速度.运行速度V85是一个系统性的衡量指标,考虑了公路上大多数驾驶员的交通心理需求,反映了驾驶员心理、视觉和驾驶行为的实时变化.
本文通过北京市四座典型的互通立交匝道上车辆的实际行驶速度观测,经统计、分析,总结其数据分布规律,最终得到其第85位的速度值,并回归出互通立交匝道运行速度相应的测算模型.
2.3 互通立交匝道运行速度影响因素
车辆运行速度的主要影响因素有几何参数、交通参数和环境参数三个方面[4].
(1)公路几何参数:平曲线半径、超高、加宽、纵坡坡度、道路横断面尺寸、交通设施设置等都会对车辆运行速度产生一定影响.
(2)交通参数:对车辆运行影响最主要的因素为交通量、车辆组成等.
(3)环境参数:调查时的天气情况及交通组织和管理等.
Lamm等对两车道乡村公路的设计参数影响评价研究,将平面线形中角度改变的绝对值/路线的长度定义为曲率变化率(CCRS),研究表明曲率变化率可以明显反映事故率变化和运行速度的变化[5].Krammes等人采集在自由流状态下,分布于纽约、俄勒冈、宾西法尼亚、德克萨斯和华盛顿5个州共138个平曲线上车辆的运行速度数据,认为运行速度与曲率、曲线长度和转角有关[6].Fitzpatrick对竖曲线的运行车速进行了研究,认为竖曲线的曲率是影响运行车速的显著因素,因为在竖曲线段,曲率的大小直接影响了驾驶人的视距状况[7].周琳以立交平面线形设计中的两种基本线形——圆曲线、缓和曲线作为构成立交线形设计中的线形元,将行车条件、线形几何约束、超高要求等约束条件,采用模糊优化设计方法,建立了模糊优化数学模型.
通过对互通立交匝道运行速度国内外的经验总结和运行速度影响因素的系统分析,可得出平曲线半径对车辆运行速度具有最重要的影响,道路超高对车辆运行也具有一定的影响.因此,确定对互通立交匝道运行速度影响较大的因素(曲率变化率、超高),排除其他影响较为微小的因素(如道路宽度、坡度等),确定调查内容,为运行速度的数据采集奠定基础.
3 基于运行速度特性的匝道分段研究
3.1 互通立交匝道分段
汽车在匝道的行驶过程中可分为:分流减速行驶过程、匀速(或变速)行驶过程和加速合流行驶过程.相应地可将一条转弯匝道分为以下三部分:
(1)离开高速公路主要道路的减速车道(分流减速);
(2)匝道路线(匀速或变速);
(3)汇入高速公路主要道路的加速车道(合流加速).
为了更好地研究车辆在互通立交匝道上的运行规律,本研究采用装有高精度GPS的试验车在自由流状态下对大羊坊桥、四方桥、马家楼桥、五方桥等北京市四座互通式立交桥的匝道车辆运行速度进行试验性调查,其运行速度数据分析结果如图2–图5所示.

图2 大羊坊桥匝道运行速度变化Fig.2 The running speed change of Dayangfang interchange ramp
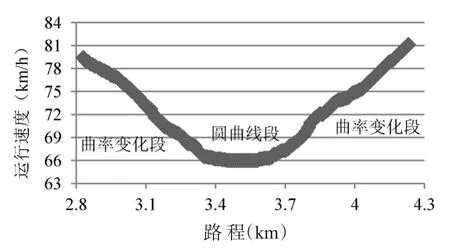
图3 四方桥匝道运行速度变化Fig.3 The running speed change of Sifang interchange ramp
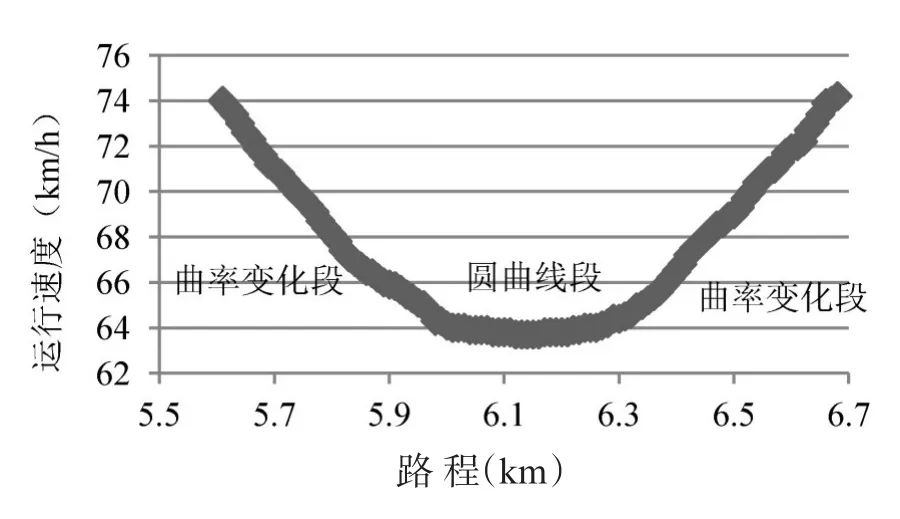
图4 马家楼桥匝道运行速度变化Fig.4 The running speed change of Majialou interchange ramp
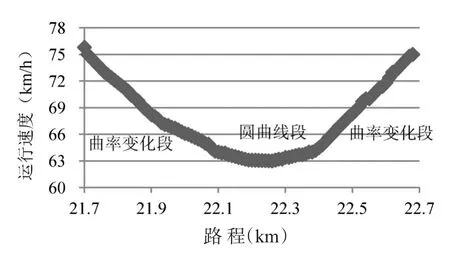
图5 五方桥匝道运行速度变化Fig.5 The running speed change of Wufang interchange ramp
从互通立交匝道的车辆连续运行速度变化数据,可以看出,匝道的车辆运行速度存在一定的相似规律,即车辆驶入匝道后,经过一段时间的减速运行后,进入匀速阶段,并且匀速阶段长度都在200 m左右,然后加速驶出匝道.因此,根据调查数据,将车辆在匝道上行驶速度依变化规律分为三段:减速段、匀速段、加速段,如图6所示.

图6 匝道分段示意图Fig.6 Interchange ramp segmentation
3.2 匝道车辆运行速度特性分析
①在行驶到出匝道时,车辆减速运行,从驶出匝道上调查所得的数据上可以看出,减速幅度为10–15 km/h,总体上运行的速度基本在(60±20)km/h.
②在平曲线的中间有一段匀速段,此路段车速基本保持不变.无论车辆是上坡与下坡,车辆运行速度变化幅度都较为相近,基本可以认为纵坡坡度对驾驶员心理没有明显影响.
③平曲线路段的末段,即与驶入匝道的连接段,车辆在路段开始处于加速阶段.车辆在此路段将接近司机的期望速度,坡度、坡长不对司机的期望速度值造成明显影响.
④车辆行驶到驶入匝道时,车辆将达到司机的期望速度,以期望速度驶入正道.
车辆从主线通过驶出匝道汇入匝道后,先一定速度进入“减速段”后,然后进入匝道的“匀速段”,最后进入“加速段”.
4 互通立交匝道运行速度数据的采集
4.1 影响因素的规定与正交试验水平划分
根据国内外研究现状及试验性的车辆运行速度各个影响因素的相关性分析可以得知,超高和CCRS两个公路线形指标对匝道加、减速段车辆运行速度的相关性影响较大,因此选择超高和CCRS两个影响因素;超高和圆曲线曲率对匝道匀速段车辆运行速度的相关性影响较大,因此选择超高和圆曲线曲率作为影响因素.
根据公路工程技术标准和实际情况及国内外的同类研究,确定互通立交匝道运行速度影响因素变化范围:超高一般在0–6%之间,CCRS一般在0–4之间.超高水平划分和CCRS水平划分如表1、表2所示.

表1 超高水平划分Table 1 The level partitions of ultra-high

表2 CCRS水平划分Table 2 The level partitions of CCRS
根据《公路路线设计规范》:匝道设计速度为30–80 km/h时,其对应的圆曲线最小半径一般值为30–280 m,圆曲线曲率=1/R,对应的圆曲线最大曲率为33.33–3.57(1/km).圆曲线曲率水平划分如表3所示.

表3 圆曲线曲率水平划分Table 3 The level partitions of Interchange circular curve
4.3 正交实验方案设计
匝道加、减速段,影响互通立交匝道运行速度的因素为超高与CCRS,该正交试验为2因素4水平试验.
匝道匀速段,影响互通立交匝道运行速度的因素为超高与圆曲线曲率,该正交试验为2因素3水平试验.
4.4 调查方案设计
选择能覆盖3个影响因素不同水平的北京市四座互通式立交共计14条匝道的小型车辆的运行速度作为研究对象,在天气良好时,根据正交实验方案,选用50名非专业司机驾驶装有高精度GPS的试验车在自由流状态下对匝道的车辆运行速度进行来回三次的实际数据调查,并获取匝道的几何参数数据:转角、坡度、竖曲线曲率、圆曲线曲率及超高等.
5 互通立交匝道运行速度模型建立
本次调查利用GPS道路线形仪对匝道线形指标进行检测,得到相应的数据.经过计算,可以得出相关影响因素(超高、CCRS、圆曲线半径)的值.同时,获得车辆在14条匝道的运行速度,该速度为点速度,以减速段的起点开始,每间隔10 m记录一个速度,同时记录该地点的超高、CCRS、圆曲线半径,最终对每个记录点的速度信息统计汇总,经排序后,以调查数据的85%车速作为车辆在该地点的计算行车速度.其中以10条匝道的数据用于构建预测模型,4条匝道的数据用于模型验证.
由调查数据中可以看出,车辆在加、减速段,CCRS对运行速度的影响最为显著,不同的CCRS对应不同的运行速度:CCRS越小,代表线形越平缓,运行速度越高,反之则越低;而当CCRS大到一定程度,其对运行速度的影响很小,甚至可以忽略不计,按平直线看待,超高对车辆运行速度也有一定影响.在匀速段,圆曲线半径与超高对车辆运行速度影响显著.
5.1 匝道减速段运行速度模型的建立
根据10条匝道的调查数据,筛选出减速段的超高和CCRS范围对应的车辆运行速度数据的平均值,选取42组有效数据,利用SPSS数据处理软件进行回归分析,得到车辆在匝道减速段的运行速度预测模型.车辆运行速度与超高、CCRS的散点图如图7、图8所示.

图7 车辆运行速度—超高散点图Fig.7 The vehicle scatter diagram of running speed—ultra-high

图8 车辆运行速度—CCRS散点图Fig.8 The vehicle scatter diagram of running speed—CCRS
在匝道减速段,超高对车辆运行速度虽然有一定的影响,呈正相关关系,但影响程度有限;而曲率变化率对车辆运行速度有较大的影响,呈负相关关系.根据调查数据,利用SPSS数据处理软件进行回归模型模拟检验,其中模型检验参数R2=0.846<1,得到车辆在匝道减速段的运行速度预测模型
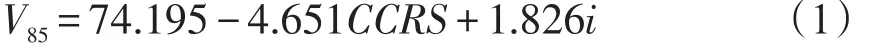
式中 V85——运行速度;
CCRS——曲率变化率(rad/km);
i——超高(%).
5.2 匝道匀速段运行速度模型的建立
根据10条匝道的调查数据,筛选出匀速段的不同超高和圆曲线曲率范围对应的车辆运行速度数据的平均值,选取42组有效数据,利用SPSS数据处理软件进行回归分析,得到车辆在匝道匀速段的运行速度预测模型.车辆运行速度与超高、圆曲线曲率的散点图如图9、图10所示.
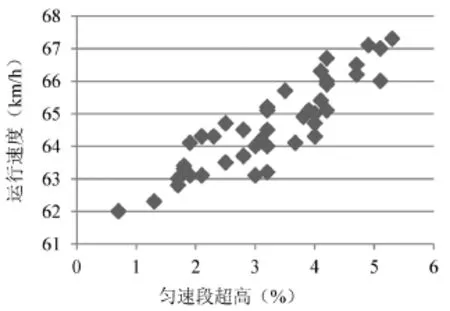
图9 车辆运行速度—超高散点图Fig.9 The vehicle scatter diagram of running speed—ultra-high

图10 车辆运行速度—圆曲线曲率散点图Fig.10 The vehicle scatter diagram of running speed—circle curvecurvature
在匝道匀速段,超高对车辆运行速度虽然有一定的影响,呈正相关关系,但影响程度有限;而圆曲线曲率对车辆运行速度有较大的影响,呈负相关关系.根据调查数据,利用SPSS数据处理软件进行回归模型模拟检验,其中模型检验参数R2=0.756<1,得到车辆在匝道匀速段的运行速度预测模型

5.3 匝道加速段运行速度模型的建立
根据10条匝道的调查数据,筛选出匝道加速段的不同超高和CCRS范围对应的车辆运行速度数据的平均值,选取42组有效数据,利用SPSS数据处理软件进行回归分析,得到车辆在匝道加速段的运行速度预测模型.车辆运行速度与超高、CCRS的散点图如图11、图12所示.

图11 车辆运行速度—超高散点图Fig.11 The vehicle scatter diagram of running speed—ultra-high
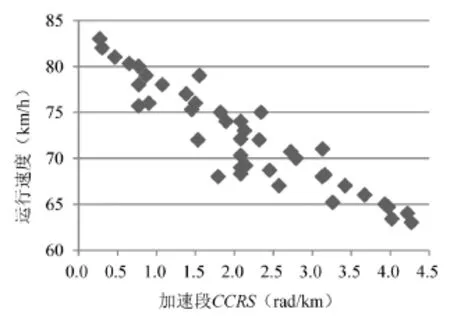
图12 车辆运行速度—CCRS散点图Fig.12 The vehicle scatter diagram of running speed—CCRS
在匝道加速段,超高对车辆运行速度虽然有一定的影响,呈正相关关系,但影响程度有限;而圆曲线曲率对车辆运行速度有较大的影响,呈负相关关系.根据调查数据,利用SPSS数据处理软件进行回归模型模拟检验,其中模型检验参数R2=0.818<1,得到车辆在匝道加速段的运行速度预测模型
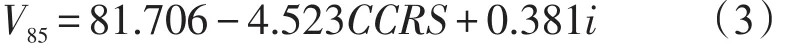
6 互通立交匝道运行速度预测模型的验证
为验证模型的准确性,需对匝道各个分段的运行速度预测模型进行检验.
对回归分析模型进行验证,一方面是为了检查模型有无异常,另一方面是分析其精度.模型精度采用相对误差来描述.
相对误差值:

相对误差的平均值:

验证数据采用剩余4条匝道的运行速度数据,从而验证减速段、匀速段、加速段三个分段匝道运行速度的预测模型.匝道各个分段预测模型预测结果与实际运行速度的观测值进行对比结果如表4所示.

表4 模型预测结果误差Table 4 Model prediction error
如表4所示,预测误差的平均值均小于5%.
7 研究结论
本文通过对互通立交匝道实际调查数据的分析研究,基于GPS道路线形检测仪的采集方法,采集了大量源自实际交通的互通立交匝道车辆运行速度数据,建立了用于互通立交运行速度模型研究分析的实测数据库;标定了适用于我国道路交通条件的互通立交运行速度模型的参数;通过数据处理软件SPSS构建匝道三个分段各自的运行速度预测模型,同时进行了相关性检测,并利用实际调查数据对模型进行了检验,模型预测相对误差在5%以内,验证了模型的正确性.
[1]中华人民共和国交通部.JTGD20-2006公路路线设计规范[S].北京:人民交通出版社,2006.[People's Republic of China Ministry of Transportation.JTGD20-2006 Highway route design specifications[S].Beijing: People's Communications Press,2006.]
[2]RuedigernLamn,Basil Psarianos,Elias M Choueiri, et al.Interchange planning and design[J].An International Perspective,Transportation Research Record,1993,1385:69-83.
[3]中华人民共和国住房和城乡建设部.GB50647-2011城市道路交叉口规划范围[S].北京:中国计划出版社,2011.[People's Republic of China Ministry of Housing and Urban-Rural Development.GB50647-2011 Range planning urban road intersections[S]. Beijing:China Planning Press,2011.]
[4]Nicholas J.Garber&Ravi Gadiraju.Factors affecting speed variance and its influence on accidents[J]. Transportation Research Record,1989,1123:64-71.
[5]Lamm R,B Psarianos,T Mailander.Highway design and traffic safety engineering handbook[M].McGraw Hill,1999.
[6]Krammes R A,Brackett R A,Shaffer M A,et al. Horizontal alinement design consistency for rural twolane highway[R].FHWA-RD-94-034,Washington D. C.,1994.
[7]Fitzpatrick K.Speed prediction for two-lane rural highways[J].FinalReP,2000,1751:59-64.
The Running Speed Prediction Model of Interchange Ramp
ZHANG Zhi-yonga,HAO Xiao-yunb,WU Wen-binb,WANG Dongb
(a.Beijing Engineering Research Center of Integrated Transportation Systems Management and Operation;b.Beijing Key lab of Transportation Engineering,Beijing University of Technology,Beijing 100124,China)
Ramp is an important part of interchange,the ramp design idea based on the running speed is a new design idea of the highway and interchange.This paper is mainly focused on the interchange ramp running speed of the vehicle.Through the analysis of the influence factors of the interchange ramp running speed,the orthogonal experiment program is formulated,and then continuous running speed data of the vehicle on the four interchanges in Beijing is collected,in total of 14 ramps with the vehicle-mounted high precision GPS devices.According to 10 of these ramps’data,based on the running speed characteristics of the vehicle on the interchange ramp,the ramp is divided into three sections:deceleration section,uniform section,acceleration section.At last,the prediction model of each section between the interchange ramp running speed and the influence factors is established,and then the prediction model is verified through comparing the remaining four ramps’measured data.The results show that the relative error values of the prediction model are less than 5%,the accuracy of the model is validated.
traffic engineering;speed;interchange;ramp;orthogonal experiment;prediction model
1009-6744(2015)01-0093-07
:U461;TP308
:A
2014-09-12
:2014-12-05录用日期:2014-12-15
国家重点基础研究发展计划(2012CB723303).
张智勇(1973-),男,四川江津人,副教授. *
:zhang5847@bjut.edu.cn
