考虑上游信号的交叉口延误计算

王 进，邹志云，葛 欢，周志浩

(1.华中科技大学 土木工程与力学学院，武汉430074；2.嘉兴市城市发展研究中心，浙江，嘉兴314000）

考虑上游信号的交叉口延误计算

王 进*1，邹志云1，葛 欢2，周志浩2

(1.华中科技大学 土木工程与力学学院，武汉430074；2.嘉兴市城市发展研究中心，浙江，嘉兴314000）

延误是交叉口交通设计和信号优化的重要评价指标.针对传统延误计算仅考虑单个交叉口的不足，本文构建了综合考虑上下游交叉口交通运行参数的延误计算模型.模型以交通波理论为基础，综合考虑了上下游交叉口的相位相序、绿灯时长、流向流量、路段长度及相位差等因素，通过计算下游交叉口队尾时空点在各相位的演变构建队尾时空多边形，计算队尾时空多边形的面积即可得到下游交叉口计算车道组的停车延误，将其加上加减速延误最终得到交叉口信号控制延误.示例分析表明，该模型与VISSIM和SYNCHRO等软件相比，延误计算精度较高.

交通工程;交叉口延误;交通波;信号交叉口；交通设计

1 引 言

延误是交叉口交通设计和信号优化的重要评价指标，自上世纪60年代以来人们已对其进行了深入研究，形成了诸多计算模型和软件，如Webster模型、SYNCHRO模型、VISSIM模型等[1].然而这些模型要么与实际误差偏大，要么建模复杂，难以满足交通设计与优化的需要.近年一些基于实时交通信息采集的交叉口延误计算方法被提出[2，3]，较大地提高了延误计算精度，然而由于其对交通运行数据的强烈依赖，难以应用于交通设计阶段.分析传统模型计算误差偏大的原因可知，传统延误计算模型一般针对单个交叉口进行，缺乏对相邻交叉口相互影响的分析.为了描述城市信号交叉口间的相互影响，一些模型在传统模型基础上进行了改进，如HCM（Highway Capacity Manual）模型[4].该模型通过构建相邻信号交叉口协调系数，以修正按孤立交叉口计算得到的延误值.然而该修正系数计算复杂，且不能定量描述上游交叉口相位相序、绿灯时长、流向流量，以及路段长度和相位差等对下游交叉口延误的影响.近年来，一些学者对信号交叉口间复杂的相互作用现象进行了深入研究，如王殿海等对交通波理论在相邻交叉口交通流分析中的应用进行了研究[5]，王进等基于交通波理论构建了关联交叉口排队长度的计算模型等[6]，这些研究为分析信号交叉口间复杂交通现象开辟了新途径.本文在这些研究基础上，通过分析上游交叉口信号及路段长度等主要交通设计参数对下游信号交叉口延误的影响机理，基于信号交叉口排队队尾的时空演化构建了考虑上游信号的交叉口延误计算模型.

参考以往研究成果，交叉口延误一般分为三类，停车延误、信号控制延误和引道延误，其中停车延误和信号控制延误应用较为广泛[7].停车延误是车辆由于在交叉口前排队使车辆处于停止状态产生的延误；信号控制延误是由于交叉口的信号控制而产生的延误，包括停车延误和加减速延误.本文主要对停车延误进行深入研究，并加上经调查统计得到的加减速延误均值，最终形成考虑上游信号的交叉口延误计算方法.

2 基本原理

本研究基于交通波原理，将上游交叉口不同相位驶出的交通流离散化为一股股均质的交通激波，通过对由于红灯信号产生的停车波、由于绿灯放行产生的以饱和流率驶出的启动波的计算，构建下游交叉口排队队尾时空图，进而计算下游交叉口的停车延误.设某时刻下游路口队尾位置为Lqk，时刻为tk，记（tk,Lqk）为排队队尾时空状态点k，则依据上游路口各相位输出流量变化和下游路口的信号状态变化逐相位推算排队队尾的时空演化，如图1所示.

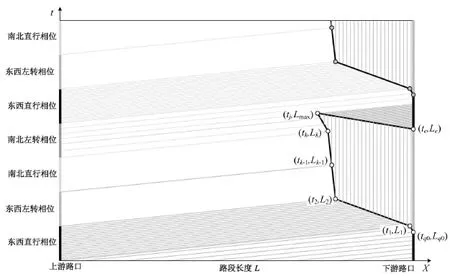
图1 考虑上游交叉口的排队长度演化Fig.1 Evolution of queue length considering about up-stream intersection

图1中，左侧条柱为上游交叉口的相位设计，右侧条柱为计算交叉口相应车道组的信号配时参数，斜线密度代表了上游交叉口各相位的输出流量中驶向下游计算车道组的流率，各圆点代表下游交叉口排队队尾时空点，其演化过程为：(tq0,Lq0)→(t1,L1)→(t2,L2)→(tk,Lk)→(tj,Lmax).其中(tq0,Lq0)为初始计算时刻的队尾时空点，(tk,Lk)为第k个队尾时空点，(tj,Lmax)为最大排队长度出现时刻队尾时空点，(te,Le)为下游路口绿灯启亮时刻排队首车通过停车线的时空点.各时空点与停车线围合的多边形即为一个周期内的队尾时空多边形，通过对队尾时空多边形面积的计算即可得到该周期内的停车延误.

由图1分析可知，考虑上游信号交叉口的延误计算可按以下5个步骤进行：

（1）上游交叉口相位流率计算.根据上游交叉口的相位设计及流向流量计算各相位输往下游交叉口计算车道组的流率.

（2）确定队尾时空演化计算起始点，以及起始点到达下游路口的车辆从上游路口驶出时所处的相位.

（3）队尾时空点演化计算.以上游路口的信号设置及各相位内的流率为基础，依据停车波逐次计算上游路口各相位驶出的车流到达下游路口时本相位末车所处的队尾时空点.

（4）最大排队长度计算.若启动波和停车波相遇，则认为最大排队长度已出现，依据启动波和停车波的变化图式即可计算得到最大排队长度值及其时空点，将各时空点与停车线围合即可得到队尾时空多边形.

（5）延误计算.计算队尾时空多边形的面积，并除以交叉口平均停车间距及信号周期内车道组的到达流量，即可得到下游交叉口计算车道组的停车延误，再加上加减速延误值，即可得到交叉口的信号控制延误.

3 模型的构建

3.1 相位流率计算

设上游交叉口第i进口左转、直行、右转的流量为FiL、FiT、FiR，各转向流量是否驶向下游计算进口道的0-1变量为ξiL、ξiT、ξiR，各转向流量是否允许在第 p相位通行的0-1变量为θiLp、θiTp、θiRp，p相位的绿灯时长为gp，交叉口的周期时长为C，下游交叉口计算车道组流量占该进口道流量的比例为η，则上游交叉口相位p驶向下游交叉口计算车道组的流率可由如下公式得到：

3.2 确定队尾时空演化计算起始点

（1）确定初始队尾时空点坐标.

当非饱和交通流时，一般下游路口绿灯末的排队长度为0，故以此时的队尾时空点(tq0,Lq0)为初始计算点.则

式中 T——相位差，s；

g——下游路口计算车道所处相位的绿灯时长，s；

若初始时刻无过饱和排队长度，Lq0=0，否则为初始时刻过饱和排队长度.

则初始队尾时空点的坐标为(tq0,Lq0)=(T+g,Lq0).

（2）计算初始队尾的车辆从上游驶出时的时刻.

计算公式如下：

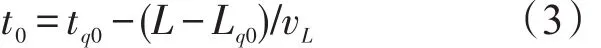
式中 L——路段长度，m；

vL——路段行驶车速，m/s.

（3）判断初始队尾的车辆从上游路口驶出时所处的相位.

即确定t0时刻上游路口所处的相位，方法如下：

① 令 p=1；② 若 t0＜gp，则 f=fp；③ 否则p=p+1，回至步骤②.

3.3 队尾时空点的演化计算

（1）队尾时空点演化计算公式.

设当前相位为 p，该相位结束时刻末车到达队尾的时空点为(tk,Lk)，则(tk,Lk)的计算如图2所示.

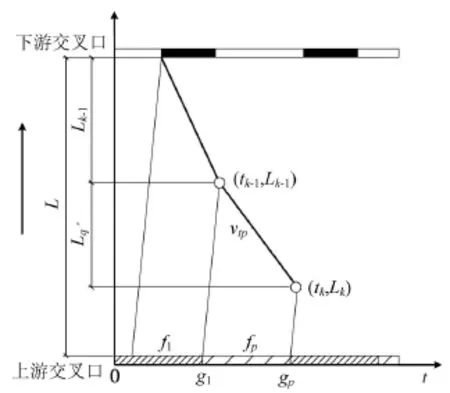
图2 队尾时空点演化计算Fig.2 Evolution of spatiotemporal coordinates of queue rear

考察上一队尾时空点(tk-1,Lk-1)至计算队尾时空点(tk,Lk)的横坐标变化，存在如下等式：

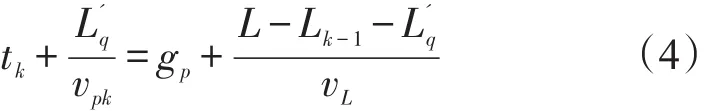
解上述方程，得到

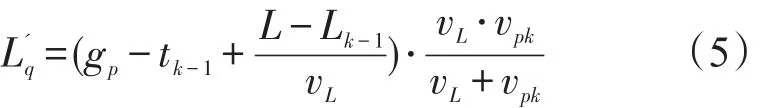
vpk——相位p车流所产生的停车波波速，m/s；

则

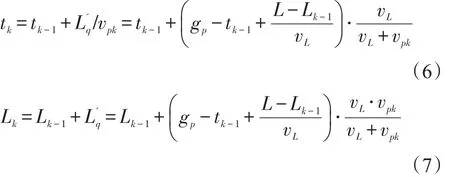
（2）循环计算.

若当前相位车流末车到达队尾时下游路口的信号灯为红灯，则需转入上游路口的下一相位继续进行排队状态的演化计算.判断上游路口当前相位车流的末车到达最大可能队尾时下游路口的信号灯状态可按下式进行：

若tk＞T+C，则下游路口为绿灯，否则为红灯.

3.4 最大排队长度计算

（1）启动波计算.

若上游路口当前相位车流的末车到达队尾时下游路口为绿灯，则下游路口的启动波已启动且开始向上游延伸，此时下游路口启动波的位置为

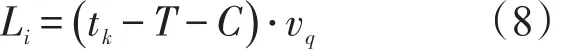
式中 vq——启动波波速，m/s.

（2）判断当前相位车流的排队车辆是否已经开始消散.

当下游路口绿灯启亮后，启动波将逐渐向上游路口延伸，若在当前相位队尾时空点计算值时刻启动波已越过了该最大可能队尾位置，则表明在该相位内排队已开始消散，此时可计算最大排队长度值，否则需转入上游路口的下一相位继续进行队尾时空点演化计算.本步骤的计算式如下：

若Li＜Lk，则 p=p+1，继续进行队尾时空点的演化计算，否则计算最大排队长度值.

（3）计算最大排队长度值.

若Li≥Lk，则当前相位车流末车到达最大可能队尾位置之前排队已开始消散，排队消散开始点的位置即为最大排队长度值，如图3所示.

图3 最大排队长度计算示意图Fig.3 The maximal queue length calculation

排队消散点至当前相位最大可能队尾时空点的时间差为

此时排队消散点的位置即为最大排队长度，其值为

3.5 延误计算

将各时空点与停车线轴围合即可得到队尾时空多边形.计算队尾时空多边形的面积，并除以平均停车间距和信号周期内计算车道组的到达流量，即可得到下游交叉口计算车道组的停车延误，公式为

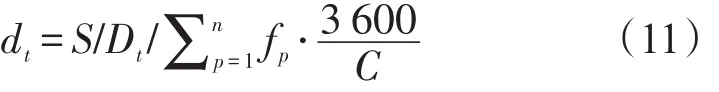
式中 S——队尾时空多边形的面积；

Dt——平均停车间距，m；

n——相位数.

下游交叉口计算车道组信号控制延误为

式中 dj——加减速延误，s，由调查分析得到.

4 案例分析

设某相邻交叉口间距300 m，均为十字交叉，各进口道均为三车道，其中直左右专用车道各一条，各进口道总流量均为500 pcu/h，左右转比例均为15%，上下游交叉口信号周期均为120 s，采用对称放行四相位控制，相序为先直后左，各相位绿灯时间均为27 s，黄灯时间3 s，路段行驶车速取10 m/s，饱和流率取1 800 pcu/h，停车间距取7.5 m，加减速延误均取2 s，计算下游交叉口直行车道的信号控制延误.

分别采用本模型、VISSIM和SYNCHRO交通软件进行计算，结果如表1所示.

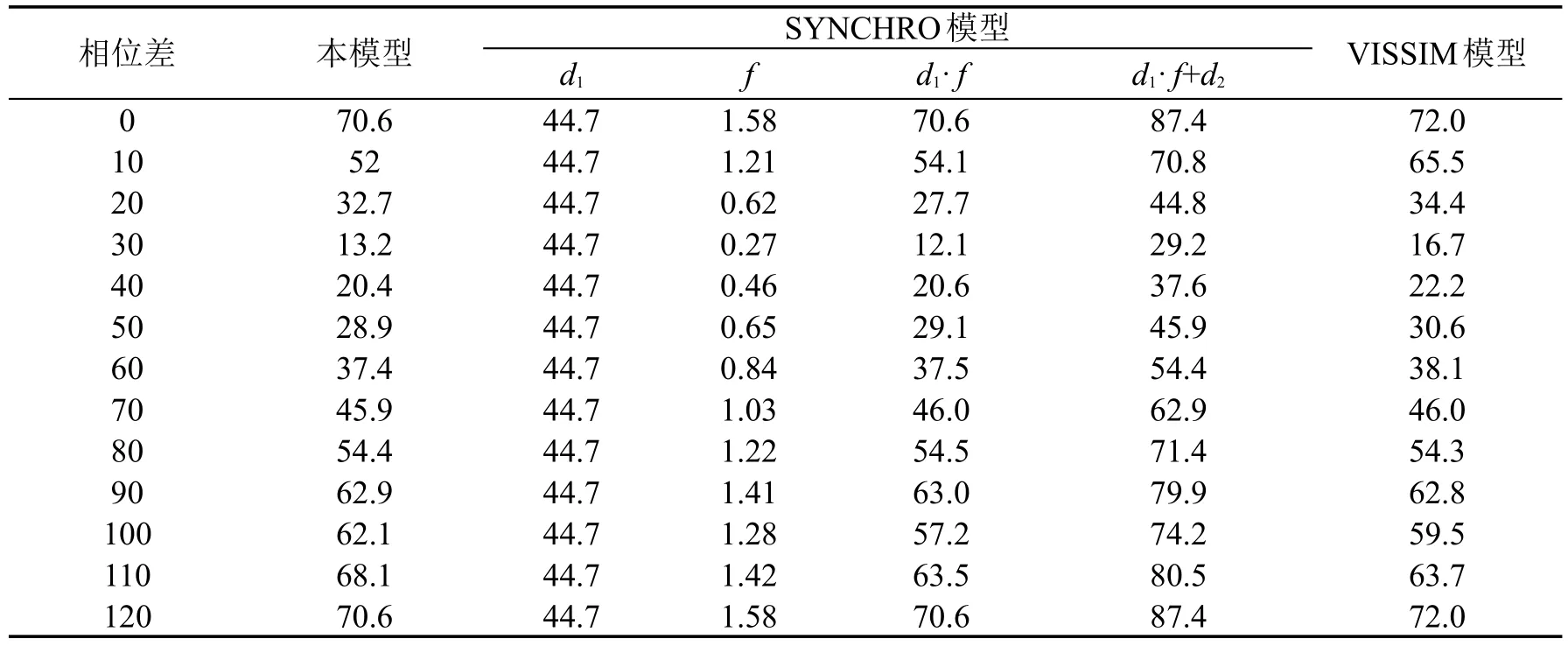
表1 交叉口延误计算示例分析Table 1 Case study for the delay calculation of a signalized intersection

图4 交叉口延误计算对比分析Fig.4 Compare analysis of the intersection delay

在图4中，d1是SYNCHRO模型中假设交通流均匀到达的延误值；f是SYNCHRO模型计算得到的上下游交叉口信号协调系数；d1⋅f是由SYNCHRO模型计算得到的交叉口延误第一项，与HCM公式中的第一项相对应；d1⋅f+d2是SYNCHRO模型给出的车道组延误值，其中d2是应用HCM中的相关公式计算得到的增量延误项；VISSIM延误是车道组车流实际行驶时间与理想行驶时间之差，图中给出的是1小时仿真时段内的统计平均值.

由图4可以看出：

① d1⋅f项、VISSIM延误及本模型计算的延误三者较接近，d1⋅f+d2项由于考虑了增量延误，与其它其计算方法相差较大，可见，对于城市道路由于信号交叉口的存在，流量到达已不再呈泊松分布等随机分布形式，车辆随机到达产生的延误影响较小.

②本模型计算误差较小，相对于SYNCHRO的平均误差为2.5%，相对于VISSIM的平均误差为5.2%.

③对于对称放行的四相位控制，延误随相位差的变化存在两个低峰值和两个高峰值，两个低峰值分别对应于上游交叉口干道方向的直行和相交道路的左转与下游信号得到较好协调的相位差设计，高峰值则相反，三种模型均能较好地反映这种变化趋势.

5 研究结论

本文构建的延误计算模型能综合反映上下游交叉口各交通设计参数对下游交叉口延误的影响，可用于关联交叉口交通协调设计优化.本模型能充分反映上下游交叉口的信号设计和流向流量对延误的影响，可用于关联交叉口的实时信号协调优化.模型的计算值为车道组延误的期望值，考虑上游信号的交叉口延误概率分布规律有待深入研究.

[1]Francois Dion,Hesham Rakha,Youn-Soo Kang. Comparison of delay estimates at under-saturated and over-saturated pre-timed signalized intersections[J]. Transportation Research Part B,2004(38):99-122.

[2]Cesar A Quiroga,Darcy Bullock.Measuring control delay at signalized intersections[J].J.Transp.Eng.1999, 125:271-280.

[3]张惠玲,李克平,钱红波,等.基于视频双截面的信号控制交叉口延误检测[J].同济大学学报(自然科学版),2011,39(7):1013-1018.[ZHANG H L,LI K P,QIAN H B,et al.Signal control intersection delay detecting based on video double section[J].Journal of Tongji University(Natural Science),2011,39(7):1013-1018.]

[4]Transportation Research Board.Highway capacity manual[M].Washington D.C.,2010.

[5]王殿海,景春光,曲昭伟.交通波理论在交叉口交通流分析中的应用[J].中国公路学报，2002，15（1）：93-96.[WANG D H,JING C G,QU Z W.Application of traffic-wave theory in intersections traffic flow analysis[J].China Journal of Highway and Transport, 2002，15（1）：93-96.]

[6]王进,白玉，杨晓光.关联信号交叉口排队长度计算模型[J].同济大学学报（自然科学版）,2012，40（11）：1634-1640.[WANG J,BAI Y,YANG X G.Study on queue length calculation model at adjacent signal intersections[J].Journal Of Tongji University(Natural Science),2012，40（11）：1634-1640.]

[7]陈绍宽,郭谨一,王璇,等.信号交叉口延误计算方法的比较[J].北京交通大学学报,2005,29（3）：77-80. [CHEN S K,GUO J Y,WANG X,et al.Analysis and simulation on signalized intersection delay[J].Journal Of Beijing Jiaotong University,2005,29（3）：77-80.]

Intersection Delay Considering about Up-stream Signal

WANG Jin1,ZOU Zhi-yun1,GE Huan2,ZHOU Zhi-hao2
(1.School of Civil Engineering&Mechanics,Huazhong University of Science&Technology,Wuhan 430074,China; 2.Research Center for Urban Development of Jiaxing City,Jiaxing 314000,Zhejiang,China)

Intersection delay is an important evaluation index for traffic design and signal optimization.To overcome the demerit that the traditional delay calculation method considers about the isolated intersection,a new delay model is built by taking into the up-stream and down-stream intersections considerations.The model is based on the traffic-wave theory,and it synthesized analyzes the main influential parameters of upstream and down-stream intersections,such as phases,splits,movement volume,link length,offset,etc.A polygon formed by spatiotemporal coordinates of the queues rears is constructed by capturing the evolution of queue phase by phase,which area is used to calculate the stop delay of the object lane-group of downstream intersection.The intersection signal control delay can be counted by adding stop delay and acceleration-deceleration delay.Through a case study comparing with VISSIM and SYNCHRO software,it is found that the model is reliable for intersection delay.

traffic engineering;intersection delay;traffic-wave theory;signalized intersection;traffic design

1009-6744（2015）01-0075-06

：U491.1

：A

2014-04-21

：2014-07-16录用日期：2014-07-28

中央高校基本科研基金（HUST:2013QN030）.

王进（1978-），男，湖北黄陂人，讲师，博士. ＊

：wangjin_wj2002@163.com