考虑风速相关性的多风电场接入电网无功规划优化研究

高顺刚，褚洪川，高一涵(国网大连供电公司，辽宁 大连 116000)

考虑风速相关性的多风电场接入电网无功规划优化研究

高顺刚，褚洪川，高一涵
(国网大连供电公司，辽宁 大连 116000)

随着接入电网的风电场装机容量和风电场个数增加，风电场并网后造成的影响越来越大，传统无功规划优化方法未考虑风速相关性，且难以适应新的电网结构。根据风速快速变化和风速相关性特点，研究了基于Nataf变换产生不同相关性风速样本的方法，以电网年净收益最大为目标函数，建立考虑效益-成本-风险的无功规划优化模型，采用改进遗传内点算法对模型进行求解，利用实际的多风电场接入电网进行计算分析，证明了考虑风速相关性的无功规划优化的有效性和实用性。

风速相关性；Nataf变换；效益-成本-风险；风电场；无功规划

0 引 言

近年来，国际能源短缺问题日益凸显，电力电子技术、电网控制技术不断革新，风能作为发展最成熟的可再生清洁能源越来越受到各国发电企业的重视。中国地域辽阔，风能资源较丰富，随着国家能源政策的调整[1]，风能开发已经进入了一个高速发展的新时期，越来越多的大中型风电场投入运行，取得了良好的经济效益。但由于风电的随机性和波动性，传统的无功规划方法不再适用于新的电网，国内大多数风电场均采用异步风力发电机，当并网运行时，需要向系统吸收大量无功[2-4]，风电场满出力时，系统无功严重不足，导致电压越限，潮流不合理，同时网损增加。因此，研究含多风电场的电网无功规划具有重要意义。

国内外诸多学者在无功规划优化方面做了很多研究，文献[5]提出了含多风电场的配电网无功优化模型和算法，基于多场景的理论建立无功优化的场景模型，并针对多场景的潮流计算提出了一种高效算法；文献[6]提出利用基于利用拉丁超立方采样的蒙特卡洛模拟嵌入非支配排序遗传算法求解多目标无功规划模型的方法；文献[7]提出利用随机模拟的方法来求解无功容量优化的机会约束模型；文献[8]基于无功电压运行特性，对酒泉风电基地接入电网的无功补偿和输电通道输送能力进行研究，提出了典型情况下电网无功补偿配置方案；文献[9]基于场景概率的分析方法，更准确地建立了含有风电场的电力系统无功规划优化数学模型，并利用混合算法进行优化求解；文献[10]考虑风电机组输出功率变化对电网的影响，采用改进遗传内点算法对含风电场的电力系统进行无功优化。虽然上述研究取得了一定理论成果，但均未考虑风电场之间的风速相关性，而风速相关性对于系统的影响不容忽视，因此，在充分考虑各风电场的风速相关性，采用Nataf变换分析相关性风速的产生，提出了结合效益-成本-风险的综合无功规划优化模型，并利用实际算例验证了考虑风速相关性下的无功规划优化结论的实用性。

1 相关性风速的Nataf变换

1.1 风速概率分布描述

考虑多风电场接入的电力系统无功规划优化，需要充分结合各风电场的风电出力波动性，风电功率与风速有直接关系，通常各风电场的年平均风速的概率密度函数f(v,c,k)和累积分布函数F(c,k)可以用Weibull函数[11，12]来描述。

f(v,c,k)=kc(vc)k-1exp[-(vc)k]

(1)

F(c,k)=1-e-(v/c)k

(2)

式中，v、k、c分别代表风电场的风速、形状系数以及反映风电场年平均风速的尺度系数。风电机组的有功出力可以用分段函数形式来描述为

(3)

式中，PW为单风电机组有功出力；v、vin、vR、vout分别为当前风速、切入风速、额定风速和切出风速；PR为单风电机组额定有功功率。

1.2 风速Nataf变换

1.2.1 相关系数矩阵

相关系数是衡量不同变量之间的相关程度，对于不同风电场A、B的风速VA和VB，其相关系数[13]rAB可以由式(4)求得。

rAB=∑Ki=1(vAi-v-A)(vBi-v-B)∑Ki=1(vAi-v-A)2·∑Ki=1(vBi-v-B)2

(4)

式中，vAi、A、vBi、B分别代表风电场A和风电场B的采样值和平均值，由式(4)知rAB=rBA，由此可以求得N个不同风电场的风速相关系数矩阵RN为

RN=[1r12…r1n
r211…r2n
⋮⋮1⋮
rn1rn2…1]

(5)

可见，RN为对称矩阵。

1.2.2 相关性风速Nataf变换

相关性变量的等效变换主要有3种方法：Nataf变换、Ronsenblatt变换和Orthogonal变换[14-16]，基本思想都是将相关非正态变量变换成独立标准正态变量。Ronsenblatt变换需要已知联合累计分布函数，很难满足工程应用，Orthogonal变换误差相对较大，因此在进行风速相关性变换时常考虑用Nataf变换。

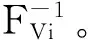
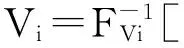
(6)

变量W的相关系数矩阵rN中元素rWij和RN中的元素rVij有如下关系。

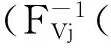
(7)

式中,μWi、σWi和μWj、σWj分别为不同风电场风速Wi和Wj的期望值和标准差；φ(Wi,Wj,rVij)是相关性系数为rVij的二维标准正态分布变量的联合概率密度函数。

rN元素的计算相对复杂，工程应用中常利用DerKiureghian和Liu给出以下的经验公式来计算。

rWij=F(rVij)rVij

(8)

+0.007rVij(σViμVi+σVjμVj)

(9)

式中，μVi、σVi和μVj、σVj分别为不同风电场风速Vi和Vj的期望值和标准差。对相关系数矩阵rN进行Cholesky分解可以求出一个与之对应的三角矩阵LN为

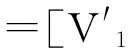
上述变化即为Nataf变换，利用上述变化的逆变换可以得到具有任意相关性的风速样本[17]。

2 综合无功规划优化模型

2.1 效益-成本-风险分析

电网无功规划优化不仅需要考虑无功补偿设备建设安装和运行检修成本[18]，还需要考虑电网安全运行风险，在允许一部分节点存在适当电压越限风险的同时，取得最大投资收益。

F=Benefit-Cost-Risk

(12)

式中，F为无功补偿后的净收益；Benefit为无功补偿后产生的经济效益；Cost为无功补偿设备安装和运行检修成本；Risk为无功补偿设备投运后引起的电网安全风险，图1表示满足电网约束条件下的效益、成本和风险之间的关系曲线。

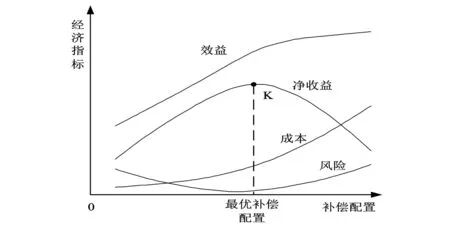
图1 效益-成本-风险曲线

效益、成本分别对无功补偿容量QC求导后，效益微增量dBenefit/dQC呈逐渐减小趋势，成本微增量dCost/dQC呈逐渐增大趋势。随着无功补偿配置容量的增加，风险指标呈先减小后增大趋势，成本的增速大于效益的增速，即收益的增加需要更多成本的投入，经济效益反而不佳，并且会带来更多的电网运行风险。净收益对无功补偿容量QC的导数dF/dQC=0时，净收益达到最高峰K点，此时对应的无功补偿配置最优。

2.2 目标函数

综合效益-成本-风险的无功规划优化目标函数，选取电网年净收益最大为目标，如式(13)所示。第一部分为效益经济指标，表示由于无功补偿设备的投入，有功损耗进一步减少所带来的经济效益；第二部分为成本经济指标，包括无功补偿设备的购置安装和运行检修费用；第三部分为风险经济指标，定义为电网各节点电压越限值与越限概率乘积再乘以电压越限惩罚费用因子。

maxF=T·Pr·ΔPloss-∑ni=1(QBi+QRi)-

∑kj=1Pkj·Kv|ΔVAj|

(13)

式中，T为系统累计运行时间；Pr系统单位电价；ΔPloss为系统无功补偿前和补偿后网损的减少量；QBi为购置安装费用；QRi为运行检修费用；Pkj为电压越限概率；Kv为电压越限惩罚费用因子；VAj为实际运行电压；ΔVAj为电压越限值，参与计算时取电压绝对值。

2.3 约束条件

无功规划优化的约束条件包括风电场出力在内的决定电网收敛性的等式约束(即潮流约束)和不等式约束两部分。

1)等式约束

Pi-Ui∑Nj=1Uj(Gijcosθij+Bijsinθij)=0
Qi-Ui∑Nj=1Uj(Gijsinθij-Bijcosθij)=0

(14)

式中，Pi、Qi分别为节点i处的有功功率和无功功率；Ui、Uj分别为节点i和与之相连的所有节点j处的电压幅值；Gij、Bij、θij分别为节点i和节点j之间的电导值、电纳值和相角差值。

2)不等式约束

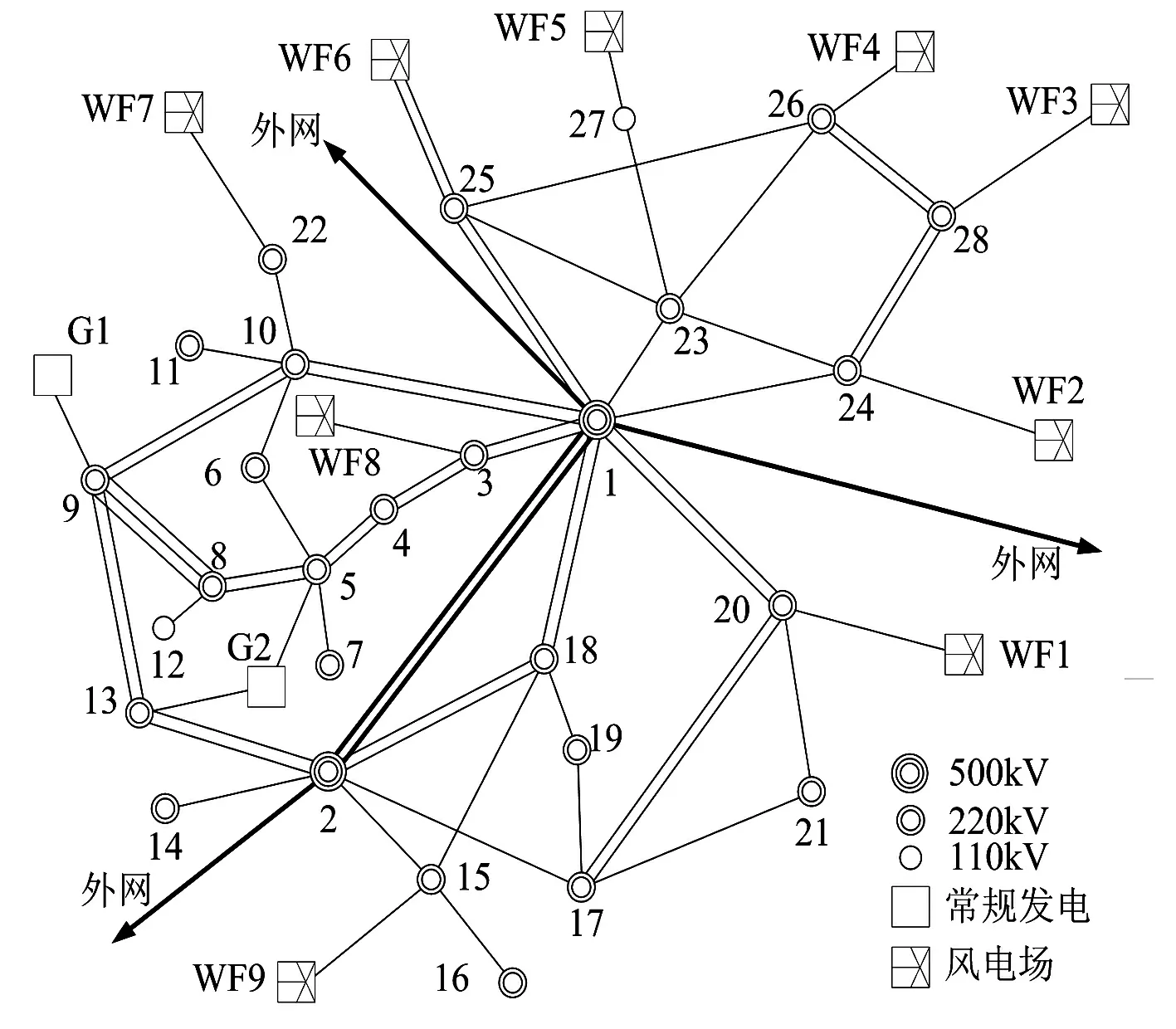
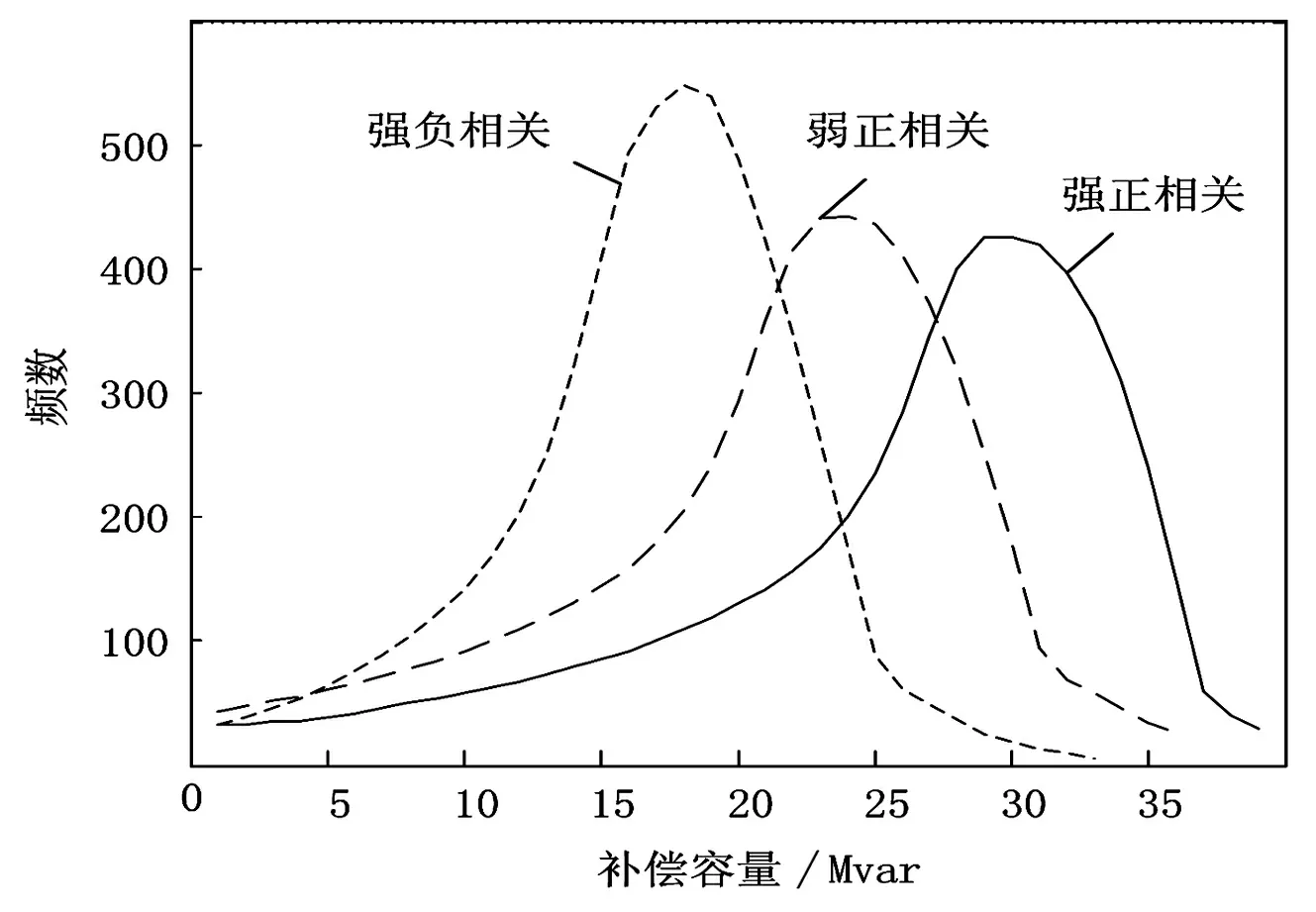
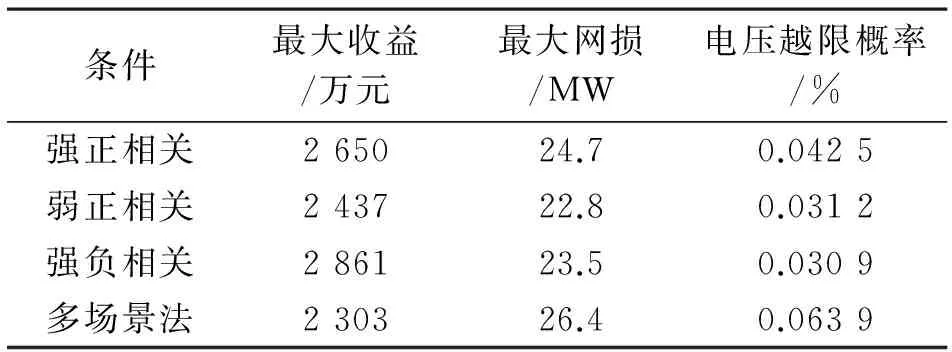
Pmin≤P≤Pmax
Qmin≤Q≤Qmax
Tmin≤T≤Tmax
QCmin≤QC≤QCmax
Pkj{Vj>Vjmax∪Vj

(15)

式中，Pmax、Pmin表示系统内包括风电机组在内的所有发电机发出的有功功率上下限；Qmax、Qmin表示系统内除风电机组外的所有发电机发出的无功功率上下限，风电场均采用恒功率因素控制，且功率因素为1，即无功输出为0；Tmax、Tmin表示系统内所有可调变压器的档位上下限；QCmax、QCmin表示系统内无功补偿节点的无功补偿容量上下限；Pkj、Pkjmax表示节点j电压越限概率和允许的电压越限概率最大值。

2.4 风电场出力和模型求解步骤

多场景分析方法的本质就是不确定性场景向多个确定性场景转换的方法，由于常规场景的选择没有考虑风电场之间的关联性，系统内部分风电场由于距离较近，风速相关性极强。模拟出的多场景并不能准确地模拟未来可能发生的场景，如所有风电场有功出力为0的场景和所有风电场满出力的场景，在实际风电场运行中，发生的概率极低。考虑风速相关性的电力系统无功规划优化，结合了各风电场自身的出力特性以及风电场出力之间的相关性，在进行系统潮流计算时，通过1.2节的方法，可以计算出各风电场的风速相关性，并将各风电场风速样本转换成具有已知相关性的多个风速样本，每个风速样本对应一个确定的风电场出力 。

综合效益-成本-风险的无功规划模型求解采用改进遗传内点算法[10]，步骤如下：①输入电网系统原始参数，获取节点和支路信息；②输入已知相关性的风速数据，计算各风电场的输出有功；③修改潮流计算中的雅克比矩阵的相关值，计算初始潮流，产生初始种群；④划分解空间，均匀分布初始群体；⑤小生境法选取算子，交叉，变异；⑥计算障碍函数，修正和计算适应度值；⑦是否达到终止条件，否则返回第⑤步；⑧是否重新启动，是则返回第④步；⑨输出结果。

表1 风电场接入容量

3 算例分析

图2 电网结构示意图

选取某实际电网进行计算分析。电网主网架如图2所示，系统共包含节点28个，其中220 kV节点24个，500 kV节点2个，110 kV节点2个，基准容量取100 MVA。该电网含常规能源发电厂两座，风电场9座，WF1至WF9依次通过节点20、24、28、26、27、25、22、3、15接入电网，除WF5接入110 kV节点外，其余风电场均接入220 kV节点，所有风电场风机均为异步风力发电机，各风电场接入容量如表1所示。优化计算中，系统内所有发电机节点的电压约束设为0.98 p.u.至1.02 p.u.，其他节点电压约束设为0.95 p.u.至1.05 p.u.，节点电压越限概率最大值取0.05，累计运行时间取5 000 h，电网电价取0.55元/kWh，无功补偿设备购置安装费取3.2万元/Mvar，运行检修费取0.15万元/Mvar，电压越限惩罚费用因子取1.5万元/kV，切入风速取3 m/s，切出风速取25 m/s，额定风速取15 m/s。允许配置无功补偿的节点包括节点1、2、3、4、5、10、13、15、17、18、20、22、23、24、25、26、27。考虑这9座风电场风速的不同相关性，选取的样本个数N=6 000，参考文献[10]所提出的改进遗传内点算法及2.4节模型求解步骤进行求解，可得到不同相关性下各无功补偿节点的补偿容量。

图3给出了各风电场风速存在强正相关、弱正相关、强负相关情况下，节点25的无功补偿容量对比。可以看出，不同相关性下节点25的无功补偿容量不相同。

图3 不同风速相关性下节点25无功补偿容量对比

强正相关和弱正相关情况下的无功补偿容量曲线相比较，出现“后移”现象，即强正相关的大量风速样本场景下，节点25的无功补偿容量偏高的累计频次大于弱正相关情况下无功无功容量偏高的累计频次。强正相关情况下，各风电场的有功出力基本一致，即当某一风电场出力达到最大时，其余风电场的出力也达到大出力水平，全网潮流也较重，全网出力波动性较大，节点电压越限的风险也较高，因此需要更大容量的无功补偿来保证电网的安全稳定运行。强正相关和强负相关情况下的无功补偿容量曲线相比较，“后移”现象更明显，强负相关情况下，同一无功补偿容量出现的最高频次大于强正相关情况下的最高频次，这说明了当风电场之间存在强负相关的情况下，各风电场出力能够起到“削峰填谷”的作用，即产生“平滑效应”，对于全网来说，波动性会减小，电压越限的风险更低，所需的无功补偿容量也较低，更有利于全网的运行。

表2 不同风速相关性无功补偿后的相关指标

表2为考虑不同风速相关性下无功补偿后的电网效益、网损以及电压越限的概率。当风速存在强正相关时，电网效益比强负相关性情况下低，无功补偿后电网网损比弱正相关、强负相关情况下的大，且电压越限概率均高于弱正相关和强负相关下的电压越限概率。各风电场强正相关的风会造成电网更大的出力波动，电压越限的风险也更大。在强负相关性下，电网效益随着无功补偿配置成本的降低而增加，由于全网的风电出力趋于平缓，无功补偿效果更明显，电压越限概率更低。利用多场景方法进行无功规划时，各项指标均大于考虑风速相关性的规划方法，主要原因在于场景选取不够合理。在进行含有多风电场的电网无功规划优化时，需要充分结合当地实际风速规律，准确把握风速相关性，尽可能全面考虑未来电网的不同场景，做到不盲目投资，但能保证电网安全运行。

4 结 论

多风电场接入的电网，由于受风电场出力波动的影响，给电网运行带来巨大风险，当风电场出力水平较高时，造成电网的无功不足。传统的无功规划方法，由于场景的选择不能准确把握地区风电特性，导致无功补偿配置不满足电网运行要求，甚至得出错误的规划结论。介绍了基于Nataf变换的相关性风速产生原理，建立了考虑效益-成本-风险的无功规划优化模型，采用改进遗传内点算法求解，通过实际算例进一步研究不同风速相关性下的无功规划优化，规划结论更具有针对性和适应性，降低了电网运行风险的同时，带来了更大的经济效益，对电网无功规划具有实际指导意义。

[1] 刘铖, 蔡国伟, 杨德友, 等. 计及风机无功约束的电压稳定性分析[J].电力系统及其自动化学报, 2013, 25(1): 1-6.

[2] 迟永宁, 刘燕华, 王伟胜, 等. 风电接入对电力系统的影响[J]. 电网技术, 2007, 31(3): 77-81.

[3] 邵志敏, 欧阳红林, 王杰, 等. 混合风电场的无功功率协调控制策略与仿真[J]. 电力系统及其自动化学报, 2012, 24(6): 62-66.

[4] 张永武, 孙爱民, 张源超, 等. 风电场无功补偿容量配置及优化运行[J]. 电力系统及其自动化学报, 2011, 23(6): 151-156.

[5] 何禹清, 彭建春, 毛丽林, 等. 含多个风电机组的配电网无功优化[J].电力系统自动化, 2010, 34(19): 37-41.

[6] 张沈习, 程浩忠, 张立波, 等. 含风电机组的配电网多目标无功规划[J]. 电力系统保护与控制, 2013, 41(1): 40-46.

[7] 江岳文, 陈冲, 温步瀛. 随机模拟粒子群算法在风电场无功补偿中的应用[J]. 中国电机工程学报, 2008, 28(13): 47-52.

[8] 王义红, 黄镔, 申洪, 等. 酒泉风电基地二期3GW风电接入电网的无功补偿设备配置及输电能力研究[J]. 电网技术, 2013, 37(5): 1440-1446.

[9] 刘沛津, 谷立臣. 含风电场的电力系统无功规划优化[J]. 电网技术, 2010, 34(7): 175-180.

[10] 魏希文, 邱晓燕, 李兴源, 等. 含风电场的电网多目标无功优化[J].电力系统保护与控制, 2010, 38(17): 107-111.

[11] 丁明, 吴义纯, 张立军.风电场风速概率分布参数计算方法的研究[J].中国电机工程学报, 2005, 25(10): 107-110.

[12] 杨秀媛, 肖洋, 陈树勇. 风电场风速和发电功率预测研究[J]. 中国电机工程学报, 2005, 25(11): 1-5.

[13] 刘燕华, 田茹, 张东英, 等. 风电出力平滑效益的分析与应用[J].电网技术, 2013, 37(4): 987-991.

[14] 陈雁, 文劲宇, 程时杰. 考虑输入变量相关性的概率潮流计算方法[J]. 中国电机工程学报, 2011, 31(22): 80-87.

[15] 牟聿强, 王秀丽, 别朝红, 等. 风电场风速随机性及容量系数分析[J].电力系统保护与控制, 2009, 37(1): 65-70.

[16] 董雷, 程卫东, 杨以涵. 含风电场的电力系统概率潮流计算[J]. 电网技术, 2009, 33(16): 87-91.

[17] 蔡德福, 陈金富, 石东源, 等. 风速相关性对配电网运行特性的影响[J]. 电网技术, 2013, 37(1): 150-155.

[18] 朱勇, 杨京燕, 高领军, 等. 含异步风力发电机的配电网无功优化规划研究[J]. 电力系统保护与控制, 2012, 40(5): 80-84.

With the increase of installed capacity and the number of grid-integrated wind farms, the impacts caused by wind farms after its integration become much greater. The traditional reactive power planning does not consider the wind speed correlation, so it is difficult to adapt to new structure of power grid. According to the fast changes of wind speed and the wind speed correlation, the method for generating wind speed samples with different correlation is studied based on Nataf transformation. It takes the maximum annual net profit of power grid as the objective function, and the optimization model of reactive power planning considering benefit-cost-risk is established. The improved genetic-interior point algorithm is adopted to solve the model, and the calculation and analysis are carried out by connecting the real multiple wind farms to power grid, which verifies the validity and practicability of reactive power planning considering wind speed correlation.

wind speed correlation; Nataf transformation; benefit-cost-risk; wind farm; reactive power planning

TM933

A

1003-6954(2015)02-0073-05

2014-12-16)

高顺刚(1964)，工程师，长期从事电力相关业务研究;

褚洪川(1987)，助理工程师，长期从事电力相关业务研究;

高一涵(1988)，助理工程师，长期从事电力相关业务研究。