电动汽车充电站布局优化方法研究综述＊

刘 锴 孙小慧 左 志

（大连理工大学交通运输学院1） 大连 116024） （名古屋大学土木工程系2） 名古屋 4648603）

0 引 言

以石油为主要燃料来源的交通领域正面临全球范围内严峻的资源与环境挑战，快速推进和发展新能源交通工具成为全世界实现交通领域可持续发展的共识.电动汽车对于缓解能源危机、气候变化、大气污染，以及日益增长的交通需求之间的矛盾具有重大意义，然而，电动汽车快速充电基础设施（以下简称“充电站”）的缺乏严重阻碍了电动汽车的推广［1－2］：能源供应空间覆盖率较低将影响出行的便利性，从而降低新能源汽车的购买意愿；另一方面，电动汽车市场需求的不确定性风险影响汽车制造商的研发投入，降低运营商投资充电基础设施的意愿.

由于电动汽车充电站建设成本较高，在有限的财政预算约束下，如何提高充电站的布局效率显得尤为重要.充电站布局问题既是空间资源的选址－分配问题，也是服务活动的选址－分配问题，其目标就是通过优化供应站的空间布局，使消费者能够获得最大效益，如获得服务的平均时间最少、需求点与供应站之间的距离最短、供应站所满足的总需求服务量最多等；同时避免充电站之间的无序竞争，满足其各自发展需求和合适的盈利水平.如果充电站布局规划时仅考虑空间覆盖率和布局密度，不仅有可能难以满足其实际充电的需求，还可能带来交通系统排队和拥堵等问题.

目前尽管有关各类新能源供应站的空间布局理论模型和实践的研究数量较多，但是全面阐述电动汽车充电站选址优化问题的综述性文献相对较少，本文旨在系统整理车用新能源供应站的空间布局优化方法和实践发展进程，为我国城市更加科学高效地开展电动汽车充电站的布局规划提供全面的思路和方法.

1 新能源供应站布局优化基本方法

1.1 新能源供应站布局优化基础模型

根据汽车能源补充需求产生的空间特征和优化方法的差异，既有新能源供应站的基本优化布局的方法和模型可归纳为两类：点需求模型和流量需求模型.这两类模型基于不同的能源补充需求假设，点需求模型适合于在家或者工作场所附近补充能源的行为习惯，而流量需求模型则更多关注途中补充能源的行为习惯，两类模型各有特色，适合于不同的环境和范围.

1.1.1 点需求基础模型 点需求模型通常假设能源补充需求产生在路网某些节点处，以需求点与供应站之间的总距离最小为优化目标，其基础模型是Hakimi于1964年提出的P－Median（也称为P中位）模型：即当能源需求的数量和位置确定，同时给定候选新能源供应站位置集合的情况下，分别为p个供应站找到合适的位置并指派每个需求点到一个特定的供应站，从而满足需求点与供应站之间的平均距离最小.

P－Median模型的数学公式表示如下.

式中：如果供应站j服务于消费者i，则Yij＝1，否则Yij＝0；如果候选点j提供新能源供应站，则Xj＝1，否则Xj＝0；hi为位置i的需求量；dij为从位置i到位置j的距离；p为供应站总数目.

P－Median模型已经在多种新能源供应站选址问题中得到了广泛应用，如美国橡树岭国家实验室关于加氢站的多项研究［3］等，其优势为：（1）模型通常将供应站选址在人们的住所或工作场所附近，符合人们补充能源的消费意愿［4］；（2）模型所需数据为基础的地理信息数据，如表示出行起讫点的人口中心点、表示候选站点的道路交叉点、道路网络、节点间的距离等，应用简便.该模型的局限性表现为：一方面补充能源需求产生的位置不仅仅局限于住所和工作场所，出行中随时可能产生需求；另一方面，该模型选址结果无法满足新能源供应站不断增加的连续性需求，即当供应站数量增加时，原来的供应站最优选址不再满足系统最优，无法满足长期发展同时保持系统最优的要求，因而缺少现实意义.此外该模型假设所有供应站都可以满足所有被指派到该处的需求，然而现实中供应站的服务容量是有限的.从实际应用来看，该类模型适合于城市规模已经稳定、新能源交通需求变化在时空分布上较为均衡的地区.

1.1.2 流量需求基础模型 流量需求模型中对能源补充需求的表示不再局限于路网中的节点，而采用路段上的车流量表示，优化目标是满足供应站所能服务的顾客流量最大，由于路段车流量计数方法的限制导致某辆在主要交通通道的车辆被重复计数，其结果往往是拥有较高流量的快速路的相邻路段都成为能源供应站的最优选址.经过改进，Hodgson［5］于1990年提出的截流选址模型（flow capturing location model，FCLM；或者flow intercepting location model，FILM），该模型的目标是布局p个供应站使得所有交通需求分配的路径中（而不是路段流量）通过供应站至少一次的车流量总和最大.FCLM模型的数学表达式［6］如下.

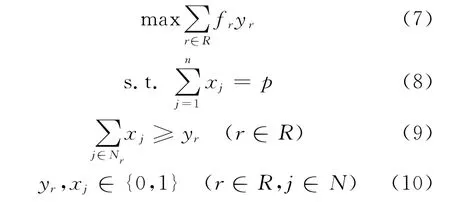
式中：若在第j个节点上设置供应站则xj＝1，否则xj＝0；若第r条路线上至少有一个服务站则yr＝1，否则yr＝0；fr表示在第r条路线上的车流量；Nr表示在路线r上的所有节点的集合；p是供应站总数目.

相比点需求模型，截流选址模型体现了新能源需求的空间分布不均衡的特征，同时较好地拟合了人们的出行行为，即人们不是为了补充能源而特地出行，而是在出行过程中顺道接受服务.FCLM模型的主要缺点是没有区别出行距离的长短和供应站的服务能力，因此该模型难以满足较长距离（例如超过100km）的出行需求，难以应用于区域供应站优化选址；忽略供应站的容量而假设路径上的供应站能够满足所有车流量的需求也是不现实的，特别是当新能源车辆逐渐增多时，该问题显得更加突出.

1.2 新能源供应站布局优化改进模型

针对P－median模型和FCLM模型存在的各种不符合实际的假设，难以解决现实问题，研究人员提出了相应的改进模型.

1.2.1 点需求改进模型 1967年Levy提出并初步解决了P－Median模型的容量限制问题［7］，即后来得到广泛研究的约束P－Median问题（capacitated P－Median problem，CPMP）：给定一个带有权重（通常表示需求量）的需求点集合，以及一个带有容量限制的备选站点集合，把需求点集合划分成p个互不相交的簇，且每个需求点仅能分配到一个簇中，使得p个簇中的距离之和最小，并且满足备选站点的容量约束.

Lin等［8］通过改进 P－median模型需求产生点的假设提出了不同的优化目标，即考虑“折返就近加油”方法（fuel－travel－back，FTB）的平均旅行时间最短的优化目标.该方法假设路网中的任一点都有可能因燃料耗尽而成为需求产生点，并且假设燃料耗尽后车辆可以“折返”至最近的能源供应站，其优化目标是当仅存在有限个能源供应站时，使所有需求产生点到离其最近的新能源供应站的总行驶时间最短.通过将FTB模型应用到南加州地区的加氢站规划，Lin等得出结论：初始加氢站应该有策略地分布，而不是一味地靠近所谓的“能源需求黄金地段”，有时甚至需要设置在低需求地点以推动氢燃料汽车的发展.

1.2.2 流量需求改进模型

1）续航选址模型 针对FCLM模型忽视储能约束下的行驶里程限制问题，Kuby和Lim［9］综合考虑行驶里程参数，建立了续航选址模型（flow refueling location model，FRLM），该模型目标是使p个供应站服务的具有行驶里程限制车辆通过途中补充能源，实现成功往返出行的流量总和最大.由于考虑了行驶里程的限制，FRLM模型更加复杂，但是更加符合现实情况，因此在实际路网中应用更易满足现实需求，如佛罗里达州的加氢站规划［10］.研究表明FRLM模型能够给出较为稳定和连续的优化布局.

FRLM模型虽然更接近现实情况，但它实际上仍只能解决能源供应站无容量限制问题，即供应站的空间和能源供给能力是无限的，能够同时服务于通过该站点的所有车辆.

2）有限容量续航选址模型 针对供应站的服务容量限制问题，Upchurch等［11］考虑了有限容量因素来修正FRLM模型，从而得到了有限容量续航选址模型（capacitated flow refueling location model，CFRLM），该模型首先假设顾客流量无限可分，将表示顾客流量是否获得服务的二元变量改为连续变量，以某OD对车流中接受某供应站组合服务的流量与该OD对全部车流量的百分比来表示；其次，基于供应站容量模块化的假设（即供应站由若干个供应设施单元组成），将表示路网某节点处是否配置供应站的二元变量变成表示该节点需要设置供应设施单元个数的整数变量.上述表示方法提高了模型对大范围区域规划的适用性，因此，CFRLM模型更加适用于现实路网.

该模型不足之处表现为顾客流量的均匀分布假设，忽略了补充能源需求在时间上的分布差异.此外，模型假设顾客对供应站的选择行为服从系统最优原则（即顾客有可能在加气加油需求实际产生之前选择供应站接受服务，以缓解车流量较大的供应站燃料供应压力），这一假设对模型来说是最理想的，却违反了现实规律.

3）考虑服务半径的截流选址模型 上述各种流量需求模型均采用了最短路径假设，即使只需绕行很短的距离就可以获得服务，也不允许有任何的绕道行为.但是现实中出行者可能乐意绕行来补充能源，而且现实世界中拥堵路段上的车流往往选择其他路径而非最短路径.文献［6］提出了考虑服务半径的截流选址模型（flow capturing location model with service radius，SR－FCLM 模型），该模型假设如果供应站距离顾客行驶路线的距离不超过服务半径d，顾客则愿意绕2d距离（往返）去接受供应站的服务.在SR－FCLM模型的基础上，杨珺等通过将顾客流量分为过路需求和固定需求建立了混合截流选址模型（hybird flow capturing location model），其目标是通过引入过路需求量的服务半径d和固定需求量的服务半径D，使得p个供应站在过路需求量的服务半径d和固定需求量的服务半径D下服务的两种顾客流量总和最大.

2 车用新能源供应站布局扩展模型

2.1 多目标选址优化模型

Current等［12］指出许多选址优化问题本质上都是多目标问题，并提出了四类值得考虑的优化目标：费用最小（cost minimization）目标、需求导向目标（demand orientation）、效益最大目标（profit maximization），以及减少环境影响目标（environmental concern）等.新能源供应站的建设费用高而资金投入有限，同时又必须保证一定的服务能力以推动新能源汽车的发展，因此多目标优化在新能源供应站布局研究中也是不可避免的选择.应用多目标模型开展选址优化研究，如满足最大覆盖／最短路径目标，可以改善能源供应站的布局效率.Wang等依据燃料消耗与添加的关系［13］，从成本效益等经济角度权衡利弊，建立了基于点需求的建设费用最小和覆盖人口最多的双目标模型，并在台湾地区得到了验证.Hodgson和 Rosing［14］将 FCLM 模型和 P－Median模型的优化目标融合，提出了服务顾客流量最大，同时需求点与供应站的总距离最小的多目标模型，可同时满足路网中的过路需求和固定需求，模型应用结果显示，P－Median模型更易受截流目标的影响.

2.2 动态选址建模方法

初始供应站的合理布局可以带动人们对新能源汽车偏好的转移，供应站与新能源汽车之间有明显的自我强化反馈.Current等［15］关注了终极发展需求具有动态不确定条件下的初始供应站布局优化问题，验证了应用最小化期望损失机会指标和最小化最大遗憾指标来解决不确定条件下的动态选址问题，并分析了两种指标的优劣势.

孙小慧等［16］在研究充电行为和充电需求的基础上，建立了满足等待时间最短和接受服务可达性最高的时空同时优化布局的动态模型，应用微观仿真方法进行了算例分析，证明时间限制下的行为决策对充电站布局存在较大影响，该动态模型对时间约束的考虑提高了优化结果的有效性.

3 电动车充电站布局未来研究方向

3.1 时间约束及时空需求分布的不确定性问题

出行起讫点的时间约束、因能源供应站同时服务能力限制而产生的排队等待等因素都会加剧时空需求的不确定性，既有模型通常建立在需求空间分布的假设基础上，而且这些模型难以同时满足区域空间需求和城市内部的空间需求［17］，因此同时考虑区域和城市交通需求的时空特征的有限容量充电站布局优化模型将是未来主要研究方向之一.考虑每个充电站的最大同时服务能力（容量限制）和最小服务范围（自我盈利和发展能力），建立动态仿真平台进行布局评价，建立区域协作服务的充电站空间规划布局模型.

3.2 基于个人决策行为的优化问题

绝大多数研究通常将人们的出行限制在最短路径上，并且假设顾客对充电站的选择行为服从系统最优原则（即顾客有可能在补充能源需求实际产生之前选择供应站接受服务，以缓解车流量较大处的某些供应站的燃料供应压力），然而，寻找合适的充电场所是一种由个人按照其主观意愿执行的行为，而不是按照交通系统或者能源服务系统的最优供给模式来制定，今后需要更多的理解个人决策（目的／路线／时间等）过程中面临的各种不确定问题，研究融合不确定性决策框架的布局方法.考虑驾驶员绕行行为和实际充电需求在空间分布不均衡时的充电站空间布局原则和方法，今后需要建立可以体现个人“期望效用最大或期望遗憾最小”而非“系统最优”决策模式下的充电站布局模型，尤其是考虑提供充电站信息和不提供信息条件下的个人决策，以及带来的网络不均衡问题.

3.3 多方式电能补充供应站的空间规划方法

城市的形态规模和交通系统状况等因素将影响电动车的使用和充电行为模式，导致充电和换电池需求的差异［18］.考虑各种城市交通流量条件和不同电动汽车市场占有率水平下，以提高充、换电站服务能力和服务水平为目标，建立时空约束的电动汽车充电站优化布局模型；考虑充、换电站初始布局和服务水平影响下的电动车市场需求演变［19］，以及对充、换电站布局的影响，是未来的重要研究内容之一.

3.4 充电站网络形成和建设时序连续性优化方法

关注充电站布局的建设时序连续性问题，即当前最优的位置在未来的供应站网络中仍是最优，或者次最优，以尽可能的降低不必要的资源浪费.在充电需求及其空间分布都具有不确定性特征条件下，连续性优化将使问题变得相当复杂，同时也会对相应的求解算法提出挑战.考虑推广初期的电动汽车需求不确定性问题及其空间分布特征，分析初始充电站的覆盖范围的时空演变特征、模式和规律，应用多智能体方法模拟其动态演化过程.

3.5 智能电网的协同控制和电价影响

既有新能源供应站布局模型往往考虑的是高峰需求，非家庭充电方式将显著增加电动汽车白天充电需求高峰期间的电力峰值压力，其结果虽然可能较好的满足交通能源补充需求，但是有可能增加电网的负担或者降低电网能效，影响电网的效率和稳定.电动汽车的推进应该成为智能电网建设和运营中的重要载体，避免高峰充电需求过大，考虑智能电网与电能需求耦合［20］的充电站布局方法对两者的协调发展至关重要.进一步研究模拟智能电网在能源分配和信息传输方面对电动汽车使用行为的影响，探索预算约束下服务水平最高的多目标优化问题解决方案，实现真正意义上的电动汽车充电站选址多目标优化.

4 结束语

布置合理数量的初始新能源供应站是克服新能源汽车与供应站先后发展困境的有力措施，为了充分利用有限的预算资金，最大限度地带动新能源汽车的发展，需要对初始供应站网络进行最优化设计.本文总结了有关新能源供应站选址优化问题的已有研究成果，通过比较点需求模型、流量需求模型、多目标优化模型、动态模型的建模思想和方法，初步探讨了各类模型存在的优缺点.各类模型越来越注重新能源汽车能源补充的实际情况，并且开始关注人们在新能源汽车时代的出行行为，但是仍然较少考虑随机产生的新能源补充需求，更多地采用了固定需求假设.

交通系统本身具有动态性和随机性特征，电动汽车的储能和充电等特性更加剧了其时空需求的不确定性，导致快速充电站的布局优化仍存在许多需进一步探讨的课题.本文进一步提出了电动汽车充电站布局研究的5个主要发展方向，包括：时空需求的不确定性问题，基于个人决策行为的优化问题，充电站－换电站结合的空间规划方法，充电站网络形成和建设时序连续性优化方法，智能电网和充电站电能供需耦合的布局优化问题，以期为电动汽车充电站的布局问题提供更加合理和高效的解决方法.

［1］SCHWOON M.A tool to optimize the initial distribution of hydrogen filling stations［J］.Transportation Research Part D，2007，12（2）：70－82.

［2］UPCHURCH C，KUBY M.Comparing the P－median and flow–refueling models for locating alternative－fuel stations［J］.Journal of Transport Geography，2010，18（6）：750－758.

［3］GREENE D L，LEIBY P N，JAMES B，et al.Analysis of the transition to hydrogen fuel cell vehicles and the potential hydrogen energy infrastructure requirements，ORNL／TM－2008／30［R］.Oak：Oak Ridge National Laboratory，2008.

［4］KITAMURA R，SPERLING D.Refueling behavior of automobile drivers［J］.Transportation Research Part A，1987，21A（3）：235－245.

［5］HODGSON M J.A flow capturing location allocation model［J］.Geographical Analysis，1990，22（3）：270－279.

［6］杨 珺，张 敏，陈 新.一类带服务半径的服务站截流选址－分配问题［J］.系统工程理论与实践，2006，26（1）：117－122.

［7］LEVY J.An extended theorem for location on a network［J］，Operational Research Quarterly，1967，18（4）：433－442.

［8］LIN Z，OGDEN J，FAN Y Y，et al.The fuel－travelback approach to hydrogen station siting［J］.International Journal of Hydrogen Energy，2008，33（12）：3096－3101.

［9］KUBY M，LIM S.The flow－refueling location problem for alternative－fuel vehicles［J］.Socio－Economic Planning Sciences，2005，39（2）：125－145.

［10］KUBY M，LINES L，SCHULTZ R，et al.Optimization of hydrogen stations in Florida using the Flow－Refueling Location Model［J］.International Journal of Hydrogen Energy，2009，34（15）：6045－6064.

［11］UPCHURCH C，KUBY M，LIM S.A model for location of capacitated alternative－fuel stations［J］.Geographical Analysis，2009，41（1）：127－148.

［12］CURRENT J R，REVELLE C S，COHON J L.The maximum covering／shortest path problem：a multi－objective network design and routing formulation［J］.European Journal of Operational Research，1985，21（2）：189－199.

［13］WANG Y W，WANG C R.Locating passenger vehicle refueling stations［J］.Transportation Research Part E，2010，46（5）：791－801.

［14］HODGSON M J，ROSING K E.A network location－allocation model trading off flow capturing and p－median objectives［J］.Annals of Operations Research，1992，40（1）：247－260.

［15］CURRENT J，RATICK S，REVELLE C.Dynamic facility location when the total number of facilities is uncertain：A decision analysis approach［J］.European Journal of Operational Research，1998，110（3）：597－609.

［16］孙小慧，刘 锴，左 志.考虑时空间限制的电动汽车充电站布局模型研究［J］.地理科学进展.2012，31（6）：692－699.

［17］UPCHURCH C，KUBY M.Comparing the P－Median and flow－refueling models for locating alternative－fuel stations［J］.Journal of Transport Geography，2010，18（6）：750－758.

［18］WANG Y W，LIN C C.Locating multiple types of recharging stations for battery－powered electric vehicle transport［J］.Transportation Research Part E，2013，58：76－87.

［19］MAK H Y，RONG Y，SHEN Z J.Infrastructure planning for electric vehicles with battery swapping［J］.Management Science，2013，59（7）：1557－1575.

［20］HE F，WU D，YIN Y F，et al.Optimal deployment of public charging stations for plug－in hybrid electric vehicles［J］.Transportation Research Part B：Methodological，2013，47：87－101.