基于 GM(1,1)和 DGM(1,1)模型的变形监测数据处理与分析
2015-04-18郭亚荣
郭亚荣
(山东科技大学资源与土木工程系,山东 泰安271000)
0 引言
近些年来,人类对变形监测的重要性逐渐有了深刻地认识,在工程施工与运营期间在建筑物周围布设了监测网并进行了重复的周期性观测,积累了变形观测数据。但由于条件的限制与人为的疏忽,观测资料的保存、分析及利用还不很完善,又因为观测数据自身所隐含的形变信息不能直接获得,所以必须对观测资料做仔细地分析与挖掘,才能更好地对变形做出正确的预测。因此对观测数据做出正确分析和处理、建立合理的预报模型是十分必要的。本文基于GM(1,1)和DGM(1,1)两个模型,以济南鲁商国奥城项目为例进行了相关的数据处理与分析。
1 理论介绍
1.1 GM(1,1)模型
GM(1,1)模型的动态模型为:
x(0)(k)+az(1)(k)=b
1)含义为一阶的一个变量的模型;
2)a称为发展系数,因为a的大小及符号,反映了x(0)(及x(1))的发展态势。
3)b为灰作用量,因为b的内涵为系统的作用量,然而b不是可以直接观测的,是通过计算得到的,是等效的作用量,是具有灰的信息覆盖的作用量,故称灰作用量。
4)z(1)(k)的序列
z(1)(k)=(z(1)(2),z(1)(3),...,z(1)(n))
z(1)(k)=0.5x(1)(k)+0.5x(1)(k-1)
称为白化背景值序列。基于每个白化背景值z(1)(k)都是x(1)(k)与x(1)(k-1)的平均值,故记 z(1)为 MEANx(1)。
1.2 DGM(1,1)模型
设非负模型:
X(0)(k)={x(0)(1),x(0)(2),…,x(0)(n)}
其一次累加生成的序列为:
X(1)(k)={x(1)(1),x(1)(2),…,x(1)(n)}
x(1^)(k )是原始序列数据的拟合值,β1、β2为待定参数,x(1^)(1 )为迭代基值。
1.3 DGM(1,1)模型与 GM(1,1)模型的关系
1)DGM(1,1)模型全面符合灰色预测模型的建模机理.是一种新的灰色预测模型.或者说是灰色预测模型的一种新形式 ;
2)原 GM(1,1)模型存在的缺陷在 DGM(1,1)中得到了解决,DGM(1,1)模型可以全面解释原GM(1,1)模型从离散形式到连续形式转变问题;
3)DGM模型可以看做是GM模型的精确形式,当GM模型中的a取值很小时,二者可替换 。
2 应用实例
2.1 工程概况
鲁商国奥城位于济南市东部,南临经十东路,北临解放东路,东临贤文路,西临规划道路。拟建区内4号楼地上42层,地下4层.按照规范和设计要求需要进行沉降观测。本工程共设水准点3个,K1、K3位于奥体中路西侧,K2位于解放东路南侧,假定K1高程为100m,水准基点采用假定高程。监测网使用的仪器为Trimble DiN03电子水准仪,水准尺为铟钢水准尺。
水准点布设图如图1所示:
2.2 基于GM(1,1)模型和DGM(1,1)模型的数据处理
选择2014年4月3日至2014年5月19日的累积沉降量作为原始数据,每五天为一期,共取10期。下面以L8、L9号点为例,其具体方法如下:
2.2.1 原始数据
两点的原始数据如表1所示。
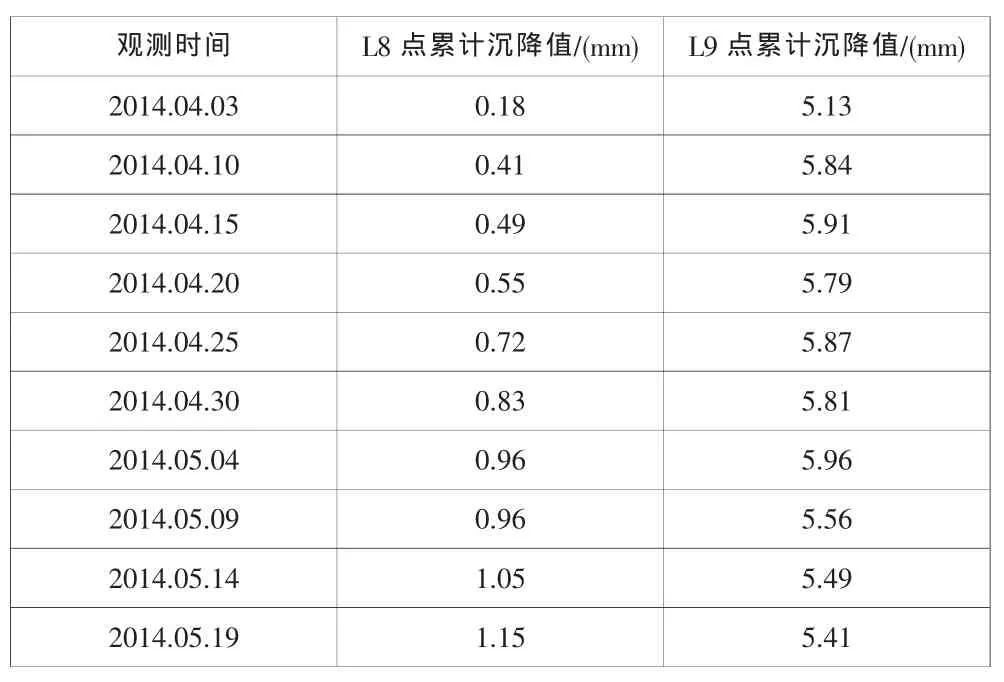
表1 原始数据
2.2.2 基于GM(1,1)模型的数据处理
使用EXCEL进行数据建模计算,该数据处理过程以L8点为例。
GM(1,1)模型原始数据序列:
X(0)=(X(0)(i))=(0.18 0.41 0.49 0.55 0.72 0.83 0.96 0.96 1.05 1.15)
X(1)={X(1)(i)}=(0.1800 0.5900 1.0800 1.6300 2.3500 3.1800 4.1400 5.1000 6.1500 7.3000)
根据z(1)(i)=0.5X(1)(i)+0.5X(1)(i-1)得出X(1)的紧邻均值生成序列Z(1)=(0.3850 0.8350 1.3550 1.9900 2.7650 3.6600 4.6200 5.6250 6.7250)
则微分方程系数向量:
a=-0.115533134
b=0.432188173
得微分方程动态模型及时间响应函数:
求出生成数的回代计算值X(1)(i)然后计算原始数据的还原值:
计算残差:
计算截图(图 2、图 3、图 4):
2.2.3 基于DGM(1,1)模型的数据处理
DGM(1,1)模型原始数据序列:
X(0)=(X(0)(i))(0.18 0.41 0.49 0.55 0.72 0.83 0.96 0.96 1.05 1.15)
X(1)={X(1)(i)}=(0.1800 0.5900 1.0800 1.6300 2.3500 3.1800 4.1400 5.1000 6.1500 7.3000)
根据上述两矩阵求解参数:
β1=0.122118491 β2=0.460034315
计算原始数据的还原值,取x(1)(1)=x(0)(1),其预测模型为:
其还原值为:
计算残差:
计算截图(图 5、图 6、图 7):
2.2.4 数据的统计分析
计算结果统计如表2所示:

表2 L8沉降数据处理统计表
同理,L9原始值与模拟值折线图
3 结论
本文通过两种模型的对比分析得出,DGM(1,1)预测模型与GM(1,1)预测模型所得出的数值结果大致相同,从实例中证明了DGM(1,1)预测模型可应用于短期沉降观测的数据处理。
[1]苗元欣.基于一元线性回归的变形监测数据处理与分析[J].山西建筑,2013(33).
[2]王永,等.利用Excel绘制误差椭圆的方法[J].矿山测量,2008,12.
[3]李水兵,李培现.基于BP神经网络的深基坑变形预测[J].测绘信息与工程,2011,10(6).
[4]王永,等.基于分形的线要素综合数据处理方法[J].矿山测量,2009,10.
[5]陈鲤江,等.数学表达式的归一化方法研究[J].浙江工业大学学报,2012(2).
