两种空间插值方法在灯塔5.1级地震烈度分布中的对比研究
2015-04-17姜金征梁永朵刘琳婷戴盈磊
姜金征,梁永朵,刘琳婷,戴盈磊,于 浩
(辽宁省地震局,辽宁沈阳 110034)
0 引言
基于强震动台网的烈度速报对于推动我国防震减灾事业的发展,促进地震监测台网资源更好地服务我国经济社会进步将发挥重要作用[1-2]。辽宁省自2007年开展强震动观测以来,至目前已拥有了82个实时传输的数据强震动台站,但利用现有台站进行烈度速报,不但台站数量不足,且分布并不均匀,需要进行空间插值才能满足烈度速报的需要[3-4]。因此,研究适当的插值方法,完成烈度等值线图的绘制成为关键。
所谓插值是通过对离散数据场插值后建立数学模型,进而提取曲线或曲面等几何信息,获取数据场内部信息并加以显示[5-6]。空间插值常用于将离散点的测量数据转换为连续的数据曲面,以便与其它空间现象的分布模式进行比较。一般常用的插值方法有距离反比加权插值法、克里格插值法、最小曲率、改进谢别德法、自然邻点插值法、最近邻点插值法、多元回归法、径向基函数法、线性插值三角网法、移动平均法、局部多项式法等。本文选用距离反比加权插值法和克里格插值方法,在应用灯塔5.1 级地震基础上,对两种方法计算结果进行了比较研究。
1 插值方法及验证
1.1 距离反比加权插值法(FIDW,Inverse Distance Weighted Interpolation)
距离反比加权插值法是基于相近相似的原理,它以插值点与样本点间的距离为权重进行平均,离插值点越近的样本点赋予的权重越大。距离反比加权插值法,可以进行确切的或者圆滑的方式插值[7]。方次参数控制着权系数如何随着离开一个格网结点距离的增加而下降。对于一个较大的方次,较近的数据点被给定一个较高的权重份额,对于一个较小的方次,权重比较均匀地分配给各数据点。计算一个格网结点时给予一个特定数据点的权值与指定方次的从结点到观测点的该结点被赋予距离倒数成比例。当计算一个格网结点时,配给的权重是一个分数,所有权重的总和等于1.0。当一个观测点与一个格网结点重合时,该观测点被给予一个实际为1.0 的权重,所有其它观测点被给予一个几乎为0.0 的权重。换言之,该结点被赋给与观测点一致的值,这就是一个准确插值(图1)。
距离反比加权平均插值是根据估算的网格中心点附近台站实际烈度值插值网格中心点烈度值,计算公式如下:

式中:Zp是相邻点的高程,d是插值点到p点的距离;n是参数,范围从1.0 至6.0,通常用的值是2.0。-n表示越靠近被插值点越重要。

图1 FIDW插值法网格示意图Fig.1 Sketch map of FIDW interpolation method
1.2 克里格法
(1)克里格法原理
克里格法(Kriging),也称空间局部估计或空间局部插值,是建立在变异函数理论及结构分析基础之上,在有限区域内对区域化变量的取值进行无偏最优估计的一种方法。该方法将任一个点的估计值通过该点影响范围内的n个有效样本值Z(xi)的线性组合得到,即

式中,λi是与样点观察Z(xi)有关的加权系数,用来表示各个样点值Z(xi)对估计值的贡献。对于任一给定的区域和数据信息Z(xi),i=1,2,…,n,存在一组加权系数 λi,λi由公式[8]确定。如果使得估计方差为最小,其区域内的真值就能在最小的可能置信区间内产生。
(2)克里格法变异分析
变异函数通过其自身的结构及其各项参数从不同的角度反映空间变异性。当空间点x在x轴上变化,区域变化量xi和xi + h在空间位置的实测值是Z(xi)和Z(xi)+ h,其中i =1,2,3,...,N(h),变异函数的离散公式为:

h为两样本点空间分隔距离。
(3)克里格法变异函数理论模型
变异函数理论模型,是当计算得到变异函数值之后,选取合适的模型进行参数的拟合,即所谓的“结构分析”。变异函数模型常用的有球状模型、指数模型、高斯模型等。
球状模型公式为:
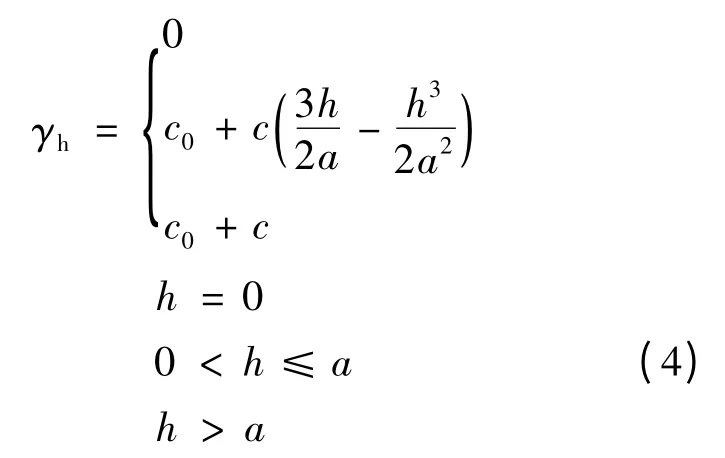
指数模型公式为:

高斯模型公式为:
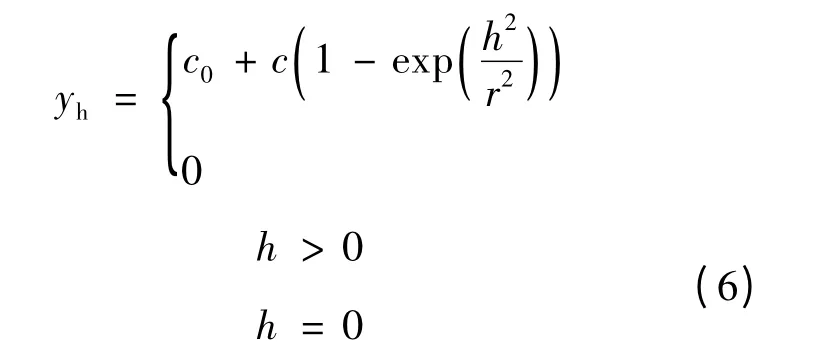
球状模型、指数模型和高斯模型对应的图形如图2所示。
(4)克里格法估算网格点烈度值
利用克里格法估算网格点烈度值主要通过以下步骤:
①先对需要插值的区域网格化,选定一个待估点,确定地理经纬度位置;②其次确定待估点最近距离3~4个已知烈度的台站;③再次根据变异函数的参数及各向异性情况,选用合适模型构造方程组;④求解方程组,得到系数λi;⑤根据公式1,求出估计点烈度值;⑥重复1~5 步,求得所有网格点的烈度值。
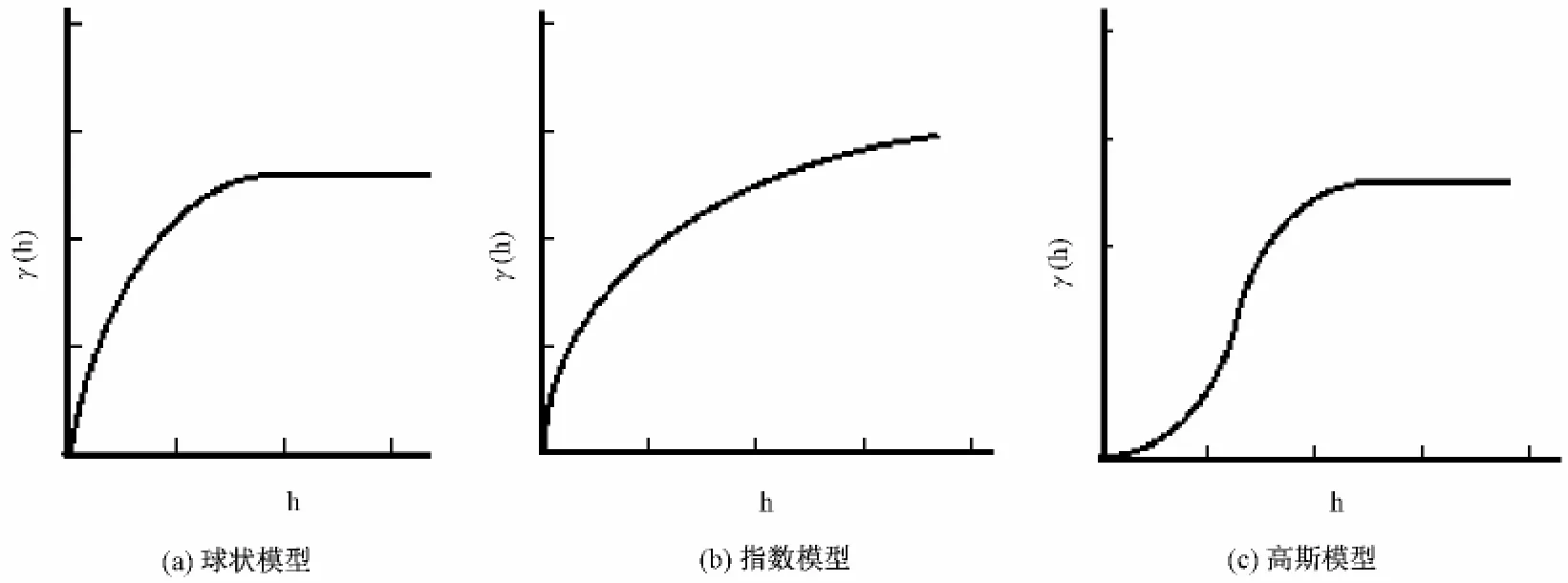
图2 三种模型示意图Fig.2 Sketch maps of the three models
1.3 空间插值方法精度评价——交叉验证法
交叉验证法是一种常见的精度验证方法。常用的交叉验证统计指标主要有平均误差(ME),平均绝对误差(MAE),平均相对误差(MRE)、均方根误差(RMSE)。ME、MAE、MRE和RMSE 的值越小,表明空间插值结果的精度越高。各指标计算公式如下:
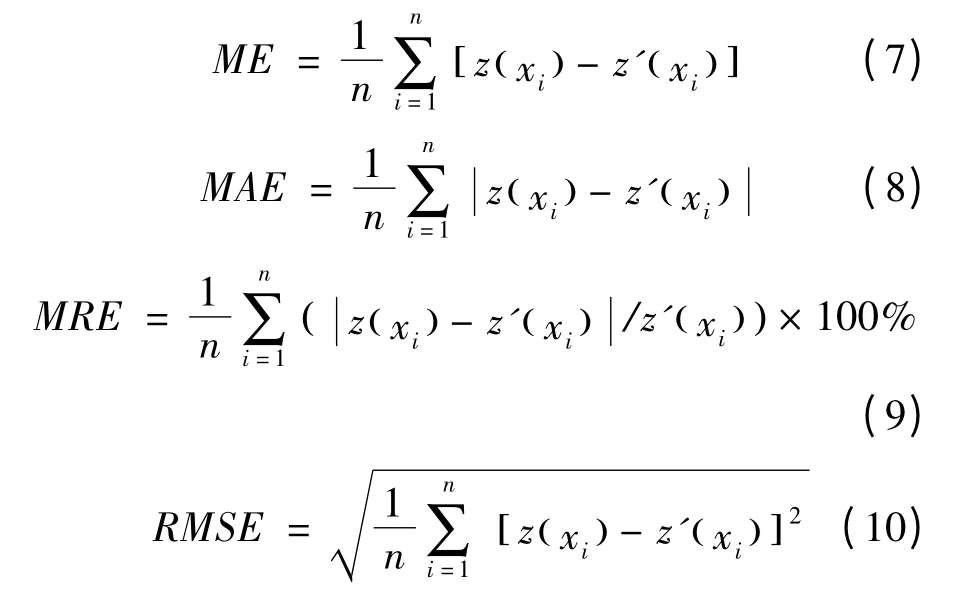
式中,z(xi)为预测值,本文中为两种空间插值法的计算结果;z'(xi)为原始采样值,本文中为宏观烈度值。
2 两种插值方法应用分析
2.1 实际震例
2013年1月23日辽宁灯塔发生了5.1 级地震,辽宁省地震局强震动台网中心回收此次地震强震动记录,剔除了两个记录有问题的台站记录,实际使用记录20 组,合计60 条,取得强震记录震中距范围从16 至370km 不等,距离震中最近的辽阳台,强震记录经校正后,水平向加速度最大峰值为21gal。本文根据各台站加速度峰值,利用美国ShakeMap 烈度计算方法[9]得到的烈度值如表1所示。
2.2 烈度图绘制
本文利用以上2 种插值方法,应用表1烈度计算结果,绘制了辽宁灯塔5.1 级地震仪器烈度分布图。绘制烈度图的具体作法如下:
(1)利用已有的台站加速度值大小构造一个粗略的、间隔统一的仿真台站网格;
(2)根据台站的加速度值,利用ShakeMap 方法确定台站的烈度值;
(3)利用距离反比加权插值法及克里格插值法构建仿真台站的烈度网格;
(4)根据烈度网格点绘制整个区域内的地震烈度分布等值线。
图3为按上述方法绘制的烈度等值线图,图中实线烈度线为距离反比加权插值法绘制,虚线烈度线为克里格插值法绘制,5 度~3 度烈度等值线由震中向外围呈环形展布。如图3所示,两种插值方法所绘烈度区域面积相当,但距离反比加权插值法图形接近于圆形,而克里格插值法接近于椭圆形。
2.3 与实际调查结果的比较
如图4所示宏观调查烈度图,是根据辽宁省地震局震害宏观调查结果以及咨询强震观测台站当值人员核实后绘制而成,烈度图由6 度~3度四个椭圆形烈度等值线组成,长轴方向与震中附近NE 向佟二堡断裂[10]走向基本一致。从图3与图4比较而言,克里格法绘制的烈度图更贴近于实际宏观调查结果。

表1 强震动记录情况Tab.1 Strong motion records
距离反比加权插值法是相近相似的原理,即离插值点越近的样本点赋予的权重越大,对邻近采样点具有依赖性,因此对台站密度及分布均匀性要求较高。而克里格法强调变量的空间自相关性,考虑了各个邻近样点彼此之间的相互关系,所以对台站密度及均匀性要求相对较低。
由图3、图4可见,图中台站分布不均匀且密度不足。因此,根据上述分析,克里格插值法相比距离反比加权插值法所绘烈度图更接近于实际调结果。但鉴于克里格法计算相对复杂,如果台网足够密集且均匀,采用计算相对简单的距离反比加权插值法更利于烈度速报需求。
由图4与图3对比可知,宏观调烈度区域范围明显大于插值方法所绘制烈度区域,这可能与插值方法所得烈度图,台站记录均为基岩台站记录,且没有经过场地校正,所以烈度区域偏小也是可以理解的。
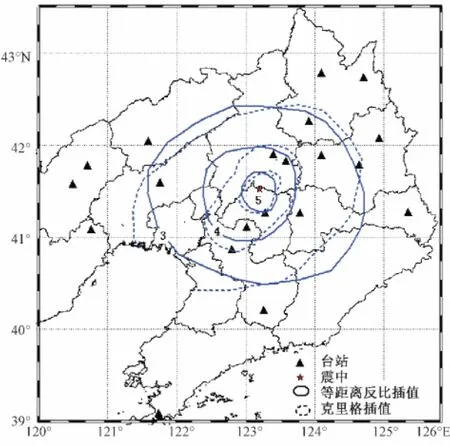
图3 烈度等值线图Fig.3 Intensity isogram
2.4 两种插值方法的精度对比
表2为两种插值方法的交叉验证结果,对比分析可知,两种插值方法误差差别不是太大,总体上看,克里格插值法的精度更高,但距离反比加权插值法的误差也在可接受范围内。故两种插值方法都可用于震后烈度估计。

表2 交叉验证误差统计结果Tab.2 Error statistics of interpolation cross validation
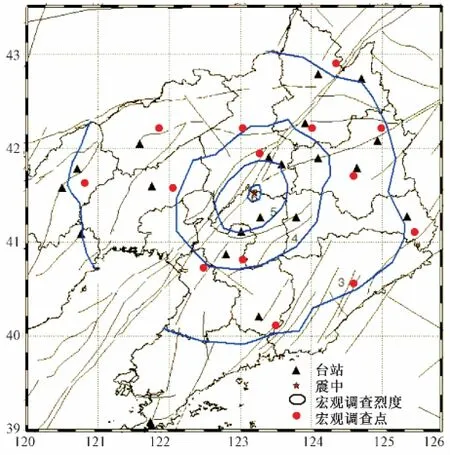
图4 宏观烈度调查结果Fig.4 Survey results of macro intensity
3 结论
本文用两种插值方法,即距离反比加权插值法和克里格插值法,绘制了灯塔5.1 级地震的烈度等值线图,并与宏观烈度调查结果进行了比较。结果发现:(1)当台站分布不均匀且密度相对不足时,采用克里格插值法绘制烈度图更符合实际宏观调查结果;(2)当台网密度较密集且分布相对均匀,本文推荐使用计算相对简单的距离反比加权插值法,此法更利于烈度速报。
[1]李山有,金星,陈先,等.地震动强度与地震烈度速报研究[J].地震工程与工程振动,2002,22(6):1-7.
[2]张敏政.地震烈度及其评定[J].防灾科技学院学报,2010(1):1-6.
[3]李永振,于沈平,金震,等.辽宁省强震台网的地震应急效果初探[J],东北地震研究,2009,25(1):37-42.
[4]李永振,翟文杰,于沈平,等.辽宁省数字强震台网建设与运行[J],东北地震研究,2009,25(3):18-22.
[5]周宝峰,温瑞智,谢礼立.非因果滤波器在强震数据处理中的应用[J].地震工程与工程振动,2012,32(2):25-34.
[6]胡进军,谢礼立.地震破裂的方向性效应相关概念综述[J].地震工程与工程振动,2011,31(4):1-8.
[7]陈晶晶,胡蓓蓓,王军,等.天津降水数据的空间插值分析[J],安徽师范大学学报,2010,33(4):15-21.
[8]靳国栋,刘衍聪,牛文杰,等.距离加权反比插值法与克里金插值法的比较[J],长春工业大学学报,2003,24(3):53-57.
[9]李俊,苏枫,米宏亮,等.ShakeMap 及其在地震动快速预估中的应用[J].中国地震,2010,26(1):103-111.
[10]单家增,张占文,孙红军,等.营口-佟二堡断裂带成因机制的构造物理模拟实验研究[J].2004,石油勘探与开发,2004,31(1):15-16.
