基于SOM和PSO的非监督地震相分析技术

张， 郑晓东， 李劲松， 路交通， 曹成寅， 隋京坤

1 中国石油勘探开发研究院， 北京 100083 2 中石化石油工程地球物理有限公司， 北京 100029



基于SOM和PSO的非监督地震相分析技术

1 中国石油勘探开发研究院， 北京 100083 2 中石化石油工程地球物理有限公司， 北京 100029

地震相分析技术是储层预测的一种重要方法，可以用来描述有利沉积相带的分布规律.传统的地震相聚类分析方法对大数据的处理运算速度较慢，且容易陷入局部极小值，造成聚类分析的结构不准确.本文提出基于自组织神经网络(SOM)和粒子群优化方法(PSO)相结合的地震相分析技术，利用自组织神经网络能够保持原始地震数据的拓扑结构特性的特点，将大量冗余样本压缩为小样本数据，再通过粒子群的全局寻优能力改善K均值聚类的效果.理论模型和实际应用表明该方法能既有效实现数据压缩，又能提供较为准确的全局解，在地震相预测中兼顾计算效率和计算精度.

自组织神经网络；粒子群算法；非监督地震相分析；聚类

1 引言

在地震储层特征描述和检测的技术中，地震相分析(Nivlet, 2007)是一种不可或缺的方法.人工地震相分析(Saggaf et al., 2003)需要投入大量的时间，更要求解释人员具有足够的经验，并结合一定的分析方法才能完成.随着勘探精度的提高，高密度、宽方位采集技术的应用，地震数据进入大数据时代，如何从海量的地震数据中提取地质特征信息成为研究的热点，近年来非监督地震相分析方法(de Matos et al., 2007)逐渐受到重视，其主要借鉴模式识别的原理，通过由地震数据得到的地震属性以及其他一些辅助信息来刻画地质体.非监督地震相分析方法(例如,Marroquín et al., 2008; Roy et al., 2010; 李芳等, 2014)完全基于数据驱动，极大地降低了人为因素的干扰，即便对于不熟悉当地地质情况的人员，也能得到一个较为客观准确的结果.

从模式识别的角度来讲，地震数据具有连续性、冗余性和一致性的特点.地震相分析本质上就是对地震数据进行分类，既可以是有监督的，也可以是无监督的.无监督的分类也叫聚类，常见的有K均值聚类方法，其主要是以k为参数，将n个对象分为k簇，使簇内具有较高的相似度.而相似度的计算主要是用每个对象到簇中心的欧几里德距离来度量.Coléou(2003)利用K均值对地震相进行聚类分析，但是该方法(韩家炜和坎伯，2001；张学工，2010)需要预先定义生成簇的数目，易受“噪声”和孤立点的影响，且不能保持数据的拓扑结构.对于连续、低维、高噪声的地震数据来说，K均值聚类不能取得较好的效果.自组织映射是由Kohonen(1982，1990)提出的一种非监督模式识别方法，其主要的思想是将数据投影到一个低维空间，以获得更为直观的理解，但它只能根据经验来判别类别数，选择最优地震属性来刻画地震数据中的地质特征.刘力辉等(1996)利用自组织神经网络进行地震微相的划分.陆文凯和牟永光(1998)利用自组织神经网络来追踪地震同相轴.Steeghs和Drijkoningen(2001)利用联合时频分析的方法来描述由地下反射信息中的微小变化会引起频率成分的波动.穆星(2005)利用自组织神经网络优选几何属性对地震相进行自动识别.Marcílio等(2007)引入小波变换的方法来识别瞬时地震道的每个地质信息段中的奇异值，该方法更易于实现SOM聚类.粒子群算法是由Kennedy和Eberhart(1997)、Eberhart和Shi(2001)对鸟类的觅食行为的研究时提出的一种基于群智能的优化方法计算. 岳碧波等(2009)通过三点滤波的方法改进粒子群的更新速度，从而使粒子更快速收敛.朱童(2011)通过前后粒子的相互作用改进了粒子群方法，从而提高了收敛速度.Liu等(2011)提出基于粒子群的多属性动态聚类方法，该方法主要利用群体智能优化方法来消除K均值聚类中奇异值对中心点选择的影响.

本文提出基于自组织神经网络和粒子群优化的K均值聚类地震相分析方法，利用SOM网络将高维的地震数据投影到低维空间，有效地保持样本空间的结构，在寻找聚类中心点时借鉴群体智能全局寻优的思想，利用粒子群方法优化自组织神经网络中神经元的聚类，最后将聚类的结果返回到原始空间中，完成地震相的分析.理论模型和实际应用均表明：利用自组织神经网络能够有效地实现数据样本空间的缩减，极大地减小数据的存储空间，缩短运算时间，再利用粒子群算法能够提供一个较为准确的全局解，两者的结合可以兼顾计算效率和精度，能够较快较好完成地震相分析.

2 自组织映射

芬兰学者Kohonen在研究联想记忆和自适应学习机时提出自组织映射，这种网络的学习机制与人类的大脑皮层上的分区自组织现象具有很多的相似性，是一种无监督的竞争性学习方法.如图1a SOM网络由输入层和输出层构成，层内无连接，层间全连接.输出层的神经元呈矩形或六边形规则地排列在同一层上.输入层中的学习样本按顺序地输入到网络空间中进行训练，输入样本的每个维度通过权值与网络上的神经元相连，而神经元之间没有相互连接，通过欧式距离来度量神经元对于输入样本的敏感度，最为敏感的神经元成为最佳匹配单元.假设训练样本x(t)的维度为N，计算i位置上的神经元向量的连接权值mij(t)与训练样本xi(t)之间欧几里德距离，即

(1)

选择最近的神经元作为最佳匹配单元，学习速率为α，邻域函数为h，更新邻近神经元，更新准则为

mij=mij+αh(mwinner,mij)(xi(t)-mij).

(2)

图1b中的红色神经元是最佳匹配单元，以它为中心，其一定范围内的临近的神经元都会受到影响，而区域外的神经元不会受到影响，这个区域就构成了相互作用的邻域.该邻域函数可定义为

或

(3)

其中，(i,j)和(m,n)分别表示最佳匹配单元和邻近神经元的位置，其形状见图1b.

在训练过程中，半径r的选择由大变小，以确保收敛，训练结束后的网络具有很好的一致性.这种算法对于邻域函数的改变表现出很好的一致性.同时，对于半径和学习速率随着训练次数的增加而减小.如图2所示，Radius轴上半部分的神经元处于兴奋状态，即神经元的连接的权重会受到一定程度的改变；Radius轴下半部分的神经元处于抑制状态，神经元的连接权重没有变化.

自组织神经网络聚类的原理是经过足够多的学习后，每个训练样本与SOM网络上神经元形成了一个确定的映射关系，即每一个样本对应网络中的一个神经元，这个神经元称为像，对应的样本，叫做原像.每一原像只有一个像，而每个像对应着样本空间中的多个原像.由于神经元的个数有限，当样本足够多时，训练好的神经元网络通过权值矩阵保留原始样本的数据结构，从而有效地实现样本数压缩，这就为大数据情况下地震相的聚类分析提供了一个基础.

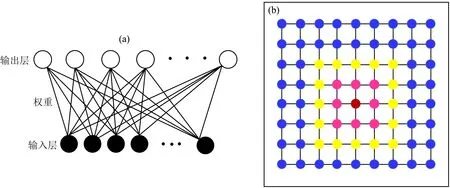
图1 自组织神经网络结构图(a)及神经元权值调整示意图(b)Fig.1 The structure of Self-Organizing Map and the sketch map of adjusting weight

图2 邻域函数图(横轴代表邻域半径，纵坐标代表神经元的响应函数；左图和右图是两种不同的神经元响应函数，R代表邻域半径)Fig.2 Neighborhood function

3 基于自组织映射和粒子群优化的K均值聚类

利用自组织神经网络实现地震数据的样本压缩后，将采用聚类方法对地震相进行划分.尽管自组织神经网络具有一定的聚类能力，但由于相邻神经元具有较高的相似性，利用该网络进行聚类分析，往往达不到预设的类别数.本文利用一种粒子群优化聚类方法对经过自组织神经网络处理的样本进行聚类划分.

Kennedy和Eberhart对鸟类的觅食行为研究时发现鸟群在飞行过程中经常会突然改变方向，散开或聚集.尽管行为不可预测，但整体上总保持着很好的一致性，同时，个体与个体之间也保持着最适宜的距离.假设鸟群在觅食的过程中，不知道食物的位置，但已知距离食物的范围.搜索的目标就是寻找离食物最近的鸟，以找到其周围的食物.由于粒子群算法采用了不同于遗传算法的随机搜索策略，因此在解决全局寻优问题时表现出极优的搜索效能.

在基本粒子群算法中，粒子群由n个粒子组成，每个粒子的位置代表优化问题在D维空间中搜索潜在的解.每个粒子根据它的位置通过优化函数计算出一个适应值，通过速度来决定其飞行方向和距离，粒子根据如下三条原则来更新自身状态：(1)保持自身的惯性；(2)按自身的最优位置来改变状态；(3)按群体的最优位置来改变状态.

设粒子的群体规模为M，则第i(i=1,2，…,M)个粒子位置可表示为Xi，它所经历的最好位置记为pbest[i]，它的速度用Vi表示，群体中最好粒子的位置的索引号用g表示，其位置表示为gbest[i].粒子更新自己的速度和位置的方式如下

(4)

Xi=Xi+Vi,

(5)

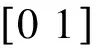
粒子群算法最初是用来处理优化问题，其搜索过程是从一组解迭代到另一组解，采用同时处理群体中多个个体的方法，具有本质的并行性；采用实数进行编码，直接在问题域上进行处理，无需转换；与遗传算法类似，粒子群算法也是多点搜索，其解的质量不依赖于初始点的选取；各粒子的移动具有随机性，可搜索不确定的复杂区，具有更有效的全局搜索能力.

K均值聚类作为一种经典算法，通过给定样本类别数和中心数实现数据的聚类分析.然而传统的K均值聚类算法具有两个固有的缺点：(1)初始值的随机化会导致不同的聚类结果，有时甚至存在无解的情况；(2)该算法基于梯度下降法，因此不可避免地陷入局部极小值(刘靖明等，2005).粒子群优化方法具有较强的全局寻优能力，将其与K均值方法结合，将K均值方法中类内中心点的求取替换为粒子群算法中粒子的搜寻，由此，可以有效地避免传统K均值方法的缺点，且能够提高精度与速度.

粒子群方法作为一种全局优化方法，结合K均值聚类，把多个神经元聚合的中心作为粒子，有速度、位置以及适应度函数构成.这里选择类内距离作为适应度函数

)1/2，

mwj为第wj类的样本中心，mi为类内样本.当类内神经元距离达到最小时，适应度函数最小.粒子群优化方法提高了寻优能力，有效避免陷入局部极小值.这种方法不但能够克服基于SOM聚类得到样本数要少于实际类别的问题，又能够大大地缩短运行时间.

① 优选能够反映地质目标的敏感属性，对地震属性进行预处理，初始化SOM网络；

② 将地震属性逐个代入网络中进行训练，根据式(1)计算神经元与样本的距离，确定最佳匹配单元，根据式(2)更新权值；

③ 如达到一定的迭代次数或是权值稳定不再改变，则训练完成，否则t=t+1，回到②；

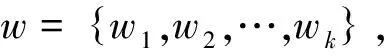
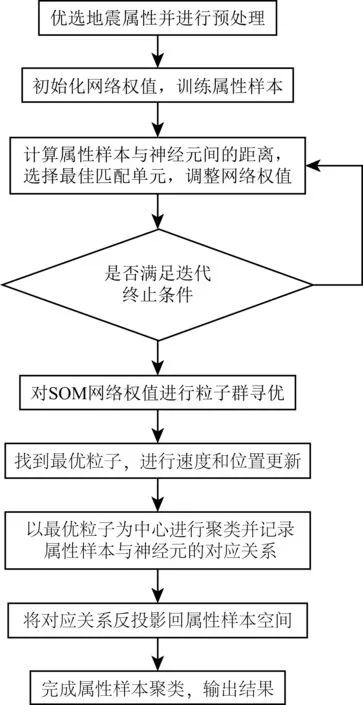
图3 算法流程图Fig.3 Flow diagram of improved method

⑤ 按照式(4)和式(5)更新所有粒子的速度和位置，再次进行聚类，并记录属性样本点与神经元的对应关系，如果满足迭代条件则算法结束，如果不满足，带入步骤④重新计算；

⑥ 将最终得到的神经网络聚类结果反映射到原来的样本空间，得到已分好类的属性样本，此时地震相聚类完成.

4 数值模拟

图4a为一个四层介质模型，第一、三和四层的速度分别为4000m·s-1，4000m·s-1和5000m·s-1，第二层的速度在横向上发生变化，分别为3000m·s-1，3300m·s-1和3700m·s-1. 为了证明该方法对于地层横向介质岩性发生变化的有效分析，本文采用一个主频为30Hz，4ms采样的雷克子波,正演得到如图4b所示合成地震记录剖面.用本文中介绍的方法将每一道数据代入到图3的算法中进行聚类分析(该模型将时间样点默认为属性)，图5a为利用本文方法得到的结果，横向上的三种变化清晰地通过三种类别展现出来，其中，不同的颜色代表不同的类别.如图5b所示，该模型在迭代初期，目标函数就近似于零，但随着迭代次数增加，目标函数值始终为零，说明该方法的稳定性好且收敛.总之，本文方法能够识别这种由于储层横向上的变化导致的地震相的不同，最终将其区分开来，即使在边界处也被很好地区分开来，同时该方法具有较好收敛特性及很好的稳定性.

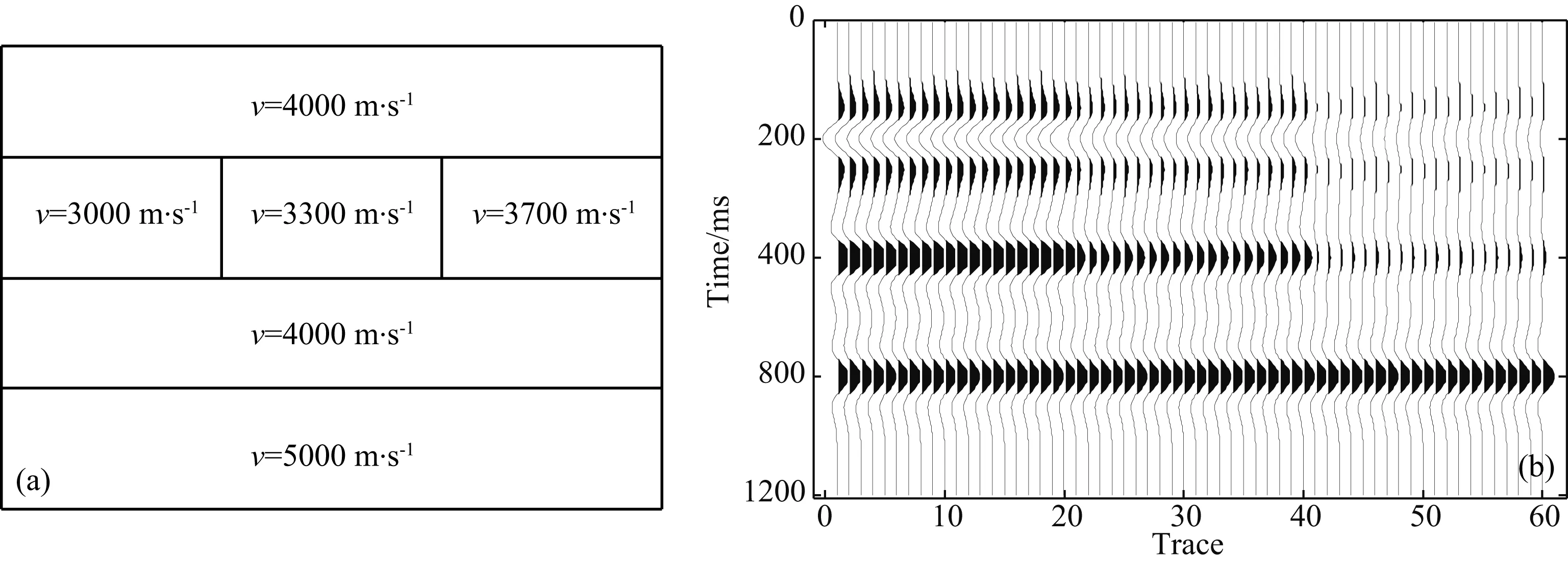
图4 地质模型(a)及其合成地震记录(b)Fig.4 Geological model (a) and its synthetic seismogram (b)

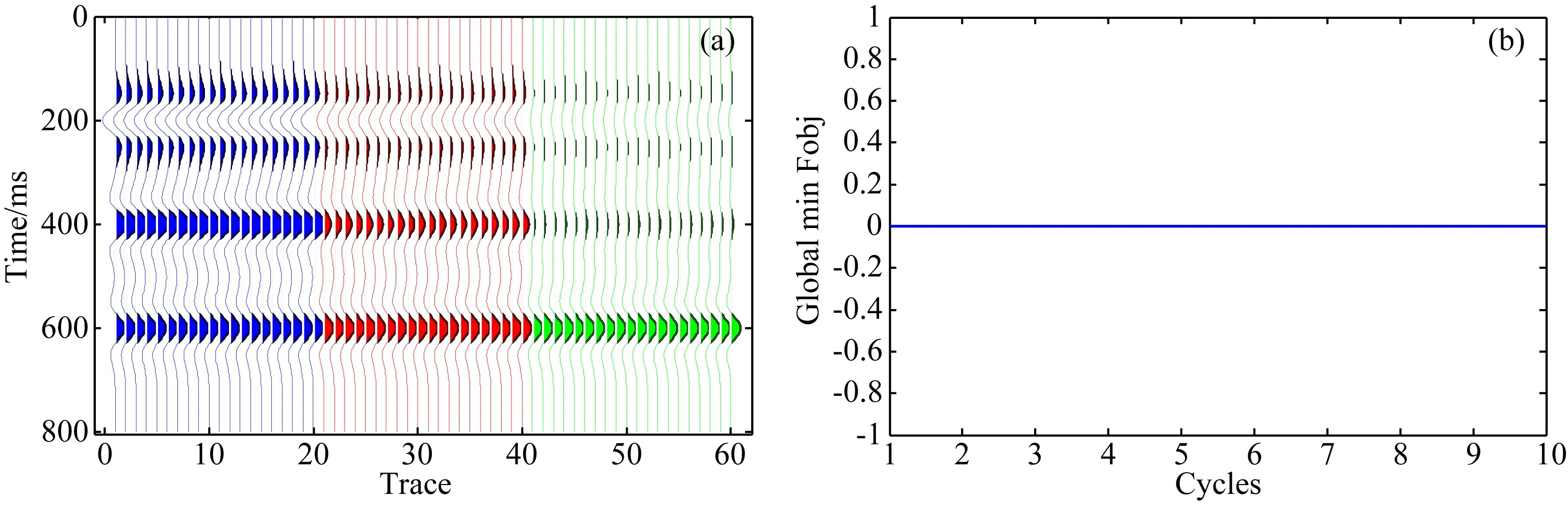
图5 聚类结果(a)和收敛函数(b)Fig.5 Cluster results (a) and convergence function (b)

图6 基于SOM和粒子群属性动态聚类结果(a) SNR=25 dB; (b) SNR=10 dB; (c) SNR=2 dB; (d) SNR<1 dBFig.6 Cluster results of seismic attribute using PSO-SOM

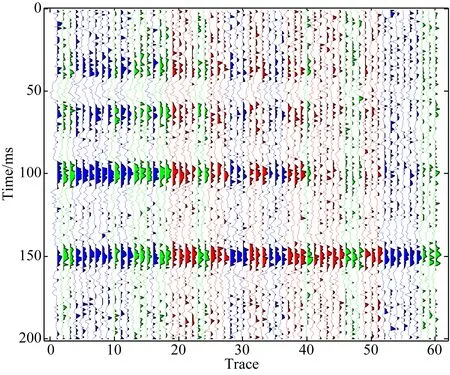
图7 某商业软件聚类结果(SNR<1)Fig.7 Cluster results with some commercial software(SNR<1)

5 实际资料处理

为了验证本文算法的实用性，选取实际工区数据加以处理，并通过工区内井资料加以验证.研究区块位于塔里木盆地中部，良里塔格族的礁滩相碳酸盐岩储层为主要目的层段，埋深约为5000m，主要岩性为泥质灰岩，地震资料的主频约为20Hz.图8为该研究工区的一条地震剖面，图中圆圈所圈位置是塔中的I号坡折带，形成于奥陶世中晚期.该地层发育了一套纵向上多旋回叠置、横向上多期次加积的较大规模的礁滩相沉积体系，主要为裂缝-孔洞性储层类型，是一套主力产层，分布于台缘坡折带上(赵文智等，2013).

图9为研究区域的地层残余厚度图，由于礁滩孔隙型储层主要受沉积相带和成岩作用控制，本文主要研究方法是在沉积层序解释的基础上，利用地层残余厚度、古地貌、岩相古地理和地震属性来分析储层和沉积相的宏观展布，利用古地形厚度图能够判别礁滩储集体空间展布特征.根据钻探井资料显示，工区内有6口钻井(见图9中黑色圆点所示)，其中，W2井、W21井、W22井和W23为工业油气井,W25井、W28井为干井或低效井.利用本文提出的方法对有利的储集相带进行预测，具体步骤如下.

(1)对目的层段提取了十多种地震属性，并结合区域的地质情况和测井资料进行分析.由于缝洞性碳酸盐岩受断裂展布的控制，最终优选具有明确的地质意义的瞬时振幅、瞬时频率、瞬时相位、曲率4种属性作为样本输入.图10a为瞬时振幅属性，红色代表振幅异常区域，表征该区域可能存在岩性或是流体变化；图10b为瞬时频率，对于裂缝存在的吸收衰减具有一定的检测作用；图10c为瞬时相位，对地震相的边缘具有很好的描述特性；图10d为相干曲率，对于断裂具有很好的预测作用.

(2)对地震数据中的空值与野值进行剔除，对优选的地震属性样本进行预处理，由于不同属性的数量级相差较大，为了便于后面的处理，将数据进行归一化处理.

图8 地震剖面Fig.8 Seismic section

图9 时间厚度图Fig.9 The figure of time thickness

(3)初始化SOM网络中的神经元，输入属性样本进行学习，通过网络权值有效地保留样本的拓扑结构，在此基础上再利用粒子群优化方法进行聚类分析，极大地减少了计算时间并将所得结果与单纯利用SOM或粒子群多属性动态方法进行比较.

图11左下角为地震属性在SOM图上的聚类结果.从图11左下角图中可知，网络权值被划分为红色、绿色和蓝色三类，将神经元与样本聚类结果的对应关系返回到原空间，就得到右侧的属性样本的结果.由于SOM上的红色区域对应的样本数据较少，在聚类结果上并没有得到很好的显示.然而，实际上一个地区地震相数目要在5～12之间，这说明SOM网络相邻聚类结果往往会低于真实数据.造成这种现象的主要原因是单纯利用SOM网络聚类，网络上临近的神经元权重具有很大的相似性，容易造成类别划分不明显，使得聚类结果显示出某种不确定性，造成划分的类别不能达到当初的期望.

图12、13和14所示分别为利用商业软件、粒子群、和本文方法所得到的结果.图中深蓝色代表台内洼地，土黄色表示礁滩相地层发育，深绿色代表丘滩相地层，红色代表有利的油气聚集带，深褐色代表断层，黄色代表斜坡.图12、13和14中礁滩相(土黄色)在空间上都显示有一定的展布特征，表征这三种方式均能在一定程度上刻画碳酸盐岩礁滩相的展布，蓝色的洼地分布也展现在地震相图中.但图12的礁滩相的边界范围与洼陷模糊不清，所以这种刻画并不准确.图13和14对礁滩相的边界和断裂带刻画都比较清晰.

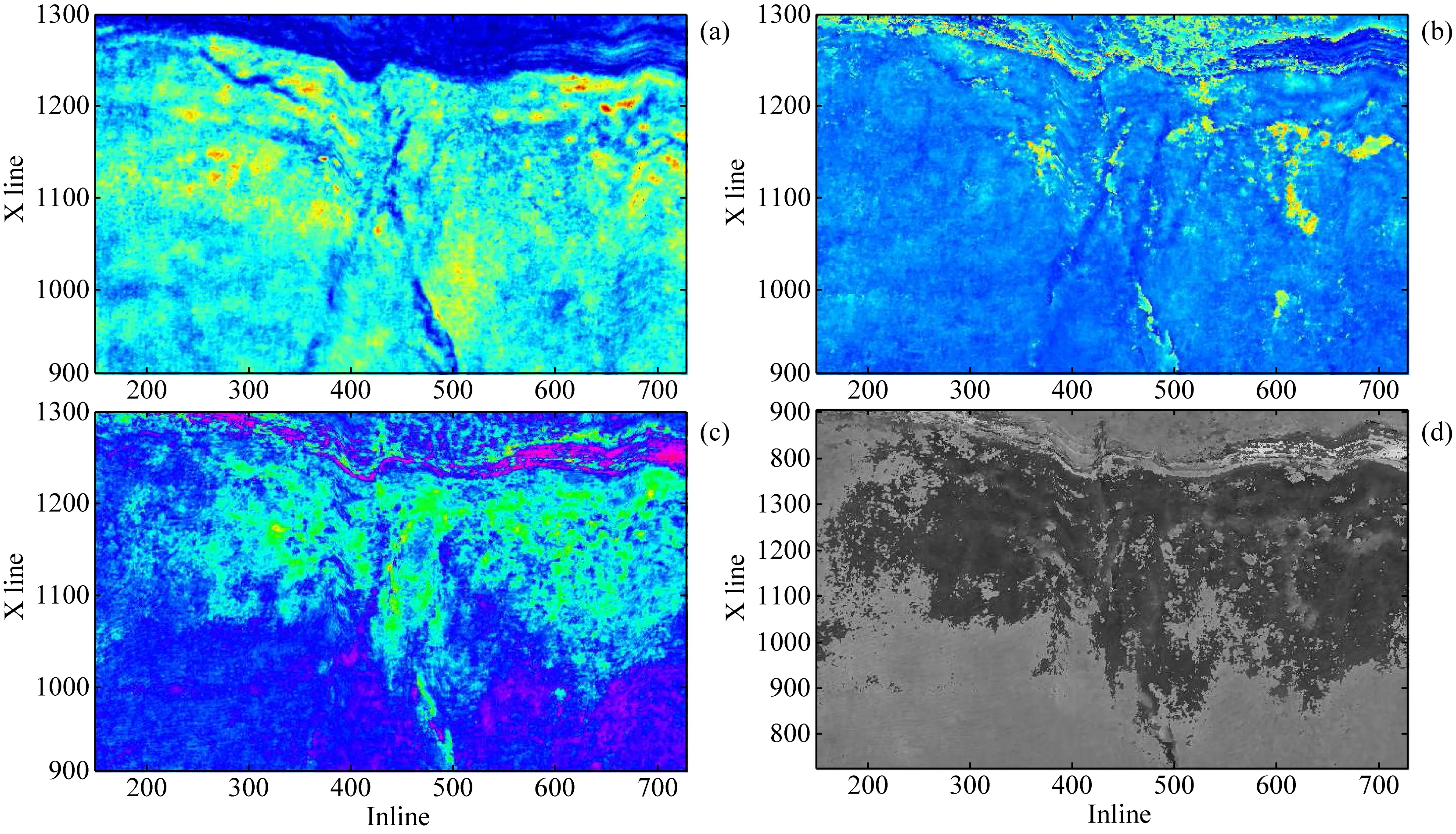
图10 地震属性图(a) 瞬时振幅; (b) 瞬时频率; (c) 瞬时相位; (d) 相干曲率.Fig.10 Seismic attribute map(a) Instantaneous amplitude; (b) Instantaneous frequency; (c) Instantaneous phase; (d) Coherent curvature.

图11 自组织神经网络分类结果和地震属性聚类图Fig.11 Cluster results in SOM and cluster results of seismic attribute using SOM

图12 某商业软件结果Fig.12 Cluster results with some commercial software

图13 粒子群聚类结果Fig.13 Cluster results of seismic attribute using PSO

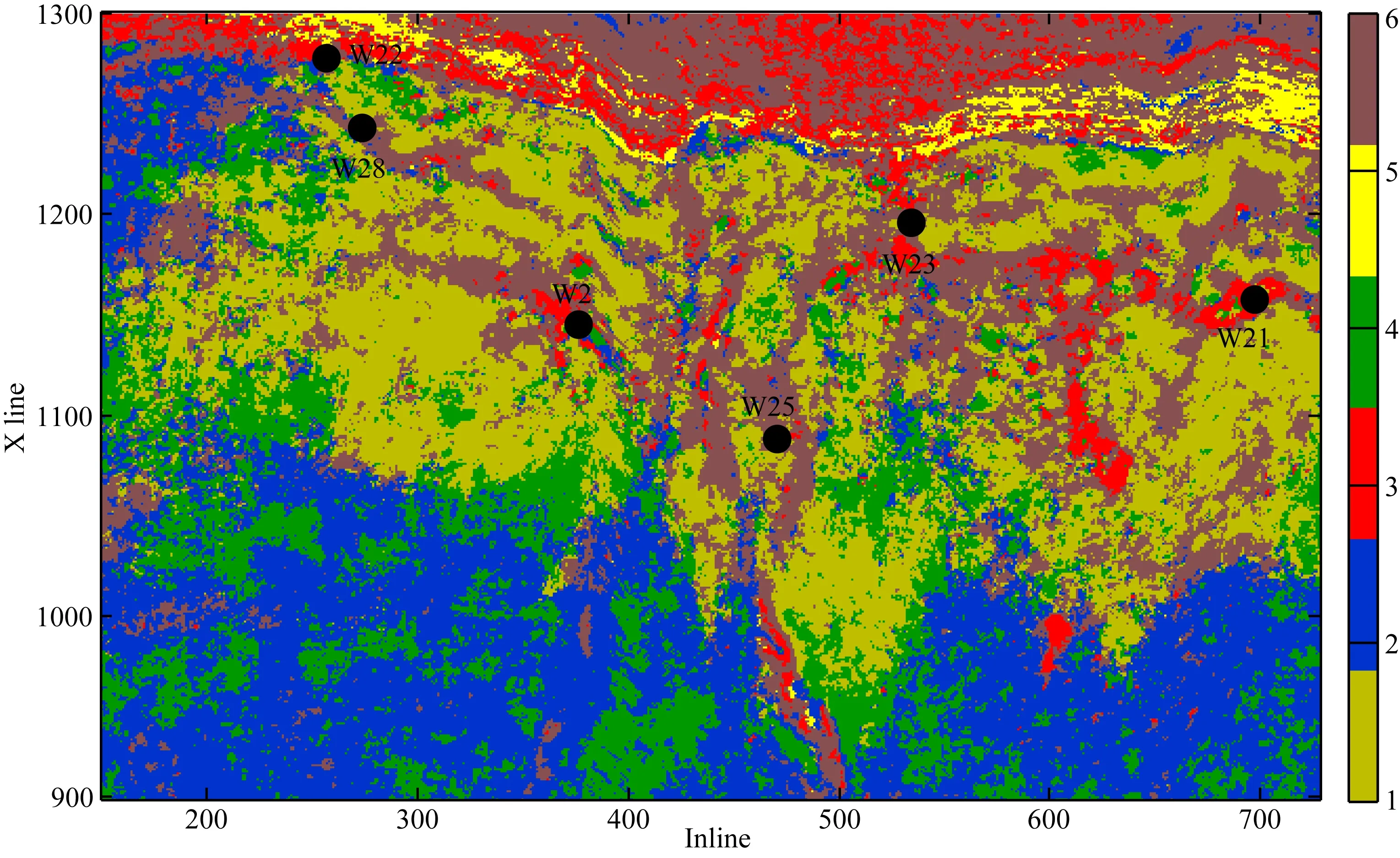
图14 基于SOM和粒子群属性动态聚类结果Fig.14 Cluster results of seismic attribute using PSO-SOM

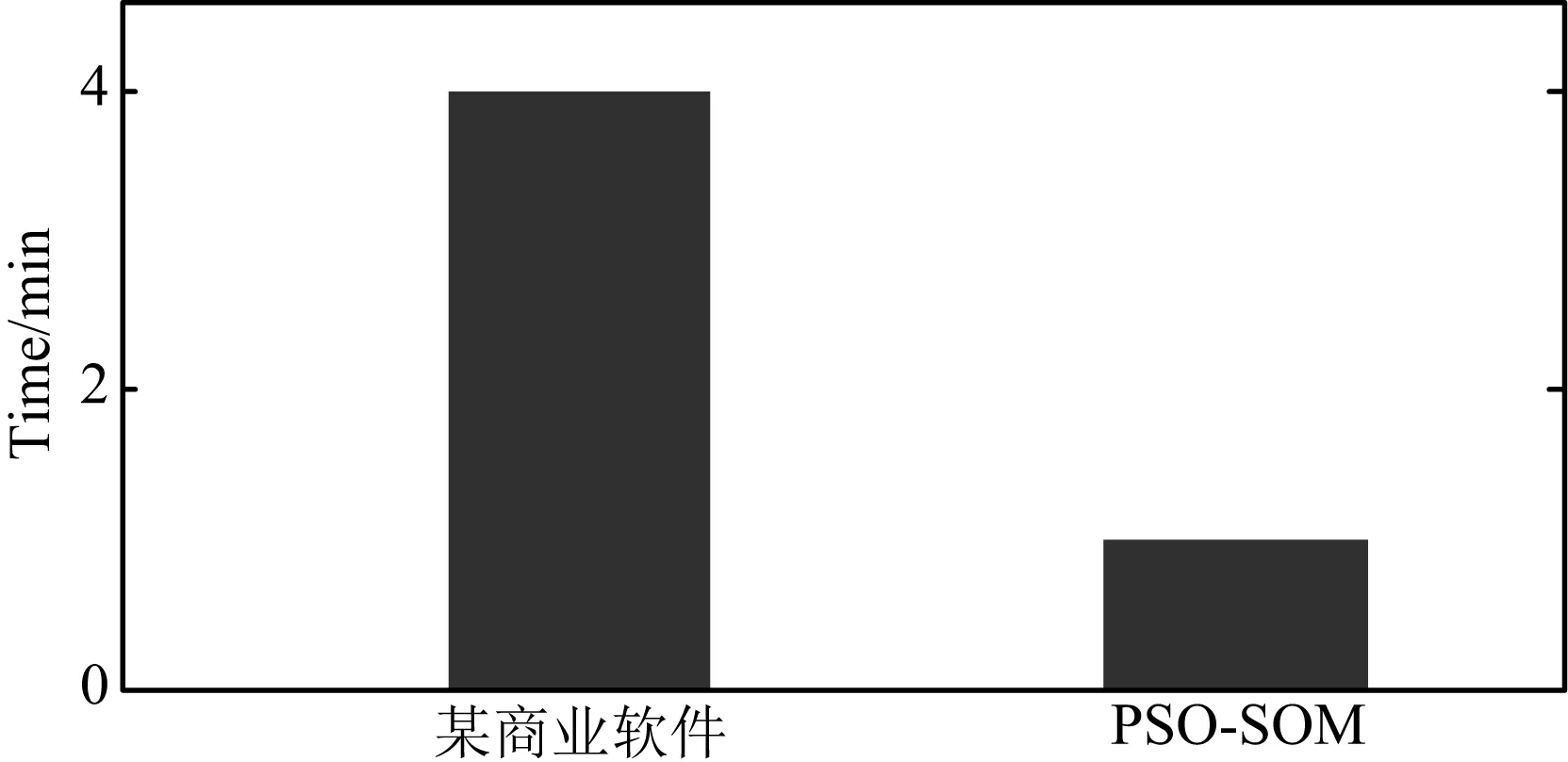
图15 计算时间对比Fig.15 Computing time

再来对比油气的预测结果，从钻录井资料获悉W2井、W21井、W22井及W23均为产油井，而在图12某商业软件处理结果中只有W21、W23落在油气聚集区(红色区域)，W2及W22落在非油气聚集区(蓝色区域)，与钻录井结果有偏差；在图13粒子群聚类结果中只有W2井、W22井、W23井落在油气聚集区(红色区域)，而W21井落在非油气聚集区(黄色区域)，这与实际情况不符；在图14本文算法处理结果中，W2井、W21井、W22井和W23均落在油气显示相带(红色区域)，W25井和W28井落在含油气性不好区域(褐色相带)，都能够与井资料较好吻合.实际资料处理加以井资料验证，说明本文算法不仅对丘滩相、斜坡以及油气分布有利相带的刻画更加清晰，而且油气预测与录井资料也比较吻合，表明本文方法有效性及实用性.

同时，为了对比本文算法在运算效率方面的优势，将商业软件处理时间与本文算法处理时间进行了比较，如图15所示.本文通过利用自组织神经网络保持原始数据拓扑结构特性的特点，将大量冗余样本压缩为小样本数据，运算时间缩短为商业软件处理的1/4，运算效率得到极大的提高.由此表明该方法具有一定的工业应用价值，尤其是将其应用到大数据处理上面.

6 结论

常规地震相分析受到海量地震数据的限制，导致计算效率较慢.本文首次提出了基于自组织神经网络和粒子群多属性动态聚类结合方法的地震相分析技术，既减小了计算工作量，又具有全局寻优能力，有效避免了陷入局部极小值，能取得较为准确的聚类.在模型数据和实际资料的应用中，以及在信噪比较差情况下，都取得了较好的聚类效果，较好揭示地震相特征，证明了本文方法的可行性及有效性.

Coléou T, Poupon M, Azbel K. 2003. Unsupervised seismic facies classification: A review and comparison of techniques and implementation.TheLeadingEdge, 22(10): 942-953, doi: 10.1190/1.1623635.

de Matos M C, Osorio P L M, Johann P R S. 2007. Unsupervised seismic facies analysis using wavelet transform and self-organizing maps.Geophysics, 72(1): P9-P21, doi: 10.1190/1.2392789.

Eberhart R C, Shi Y H. 2001. Particle swarm optimization: developments, applications and resources. ∥Proceedings of the IEEE Congress on Evolutionary Computation. Seoul: IEEE, 81-86. Han J W, Kamber M. 2001. Data Mining: Concepts and Techniques (in Chinese). Beijing: China Machine Press.Kennedy J, Eberhart R C. 1997. A discrete binary version of the particle swarm algorithm. ∥ Proceedings of 1997 IEEE International Conference on Systems, Man, and Cybernetics. Orlando, FL: IEEE, 4104-4109.

Kohonen T. 1982. Self-organized formation of topologically correct feature maps.BiologicalCybernetics, 43(1): 59-69, doi: 10.1007/BF00337288.

Kohonen T. 1990. The self-organizing map.ProceedingsoftheIEEE, 78(9): 1464-80.

Li F, Wang S D, Chen X H, et al. 2014. Oil-gas prediction with multi-attributes fusion based on fuzzy logic.OilGeophysicalProspecting(in Chinese), 49(1): 197-204.

Liu J M, H L CH, Hou L W. 2005. Cluster analysis based on particle optimization algorithm.SystemsEngineering-Theory&Practice(in Chinese), (6): 54-58.

Liu L Y, Yang M Y, Xiong J L, et al. 1996. Seismic analysis with self-organizing neutral network.OilGeophysicalProspecting(in Chinese), (S2): 90-94. Liu X F, Zheng X D, Xu G C, et al. 2011. Locally linear embedding-based seismic attribute extraction and applications.AppliedGeophysics, 7(4): 365-375, doi: 10.1007/s11770-010-0260-2.

Lu W K, Mou Y G. 1998. Seismic event automatic tracking using self-organizing neural network.GeophysicalProspectingforPetroleum(in Chinese), 37(1): 77-83.

Marroquín I D, Braulr J J, Hart B S. 2009. A visual data-mining methodology for seismic facies analysis: Part 1: Testing and comparison with other unsupervised clustering methods.Geophysics, 74(1): P1-P11, doi: 10.1190/1.3046455.

Mu X. 2005. Method of seismic facies auto-classification by the seismic geometrical attribute and the self-organizing neutral network.GeologicalScienceandTechnologyInformation(in Chinese), 24(3): 109-112.

Nivlet P. 2007. Uncertainties in seismic facies analysis for reservoir characterisation or monitoring: Causes and consequences.Oil&GasScienceandTechnology-Revuedel′IFP, 62(2): 225-235, doi: 10.2516/ogst:2007019.

PSO-based multi-attribute dynamic clustering technology and its application.SEGTechnicalProgramExpandedAbstracts, 1913-1917, doi: 10.1190/1.3627581.

Roy A, Matos M, Marfurt K J. 2010. Automatic seismic facies classification with kohonen self organizing maps-a tutorial.GeohorizonsJournalofSocietyofPetroleumGeophysicists, 6-14. Saggaf M M, Toksöz M N, Marhoon M I. 2003. Seismic facies classification and identification by competitive neural networks.Geophysics, 68(6): 1984-1999, doi: 10.1190/1.1635052.

Steeghs P, Drijkoningen G. 2001. Seismic sequence analysis and attribute extraction using quadratic time-frequency representations.Geophysics, 66(6): 1947-1959, doi: 10.1190/1.1487136.

Yue B B, Peng Z M, Hong Y G, et al. 2009. Wavelet inversion of pre-stack seismic angle-gather based on particle swarm optimization algorithm.ChineseJ.Geophys. (in Chinese), 52(12): 3116-3123, doi: 10.3969/j.issn.0001-5733.2009.12.021. Zhang X G. 2010. Pattern Recognition (Third Edition) (in Chinese). Beijing: Tsinghua University Press.Zhao W Z, Shen A J, Pan W Q, et al. 2013. A research on carbonate karst reservoirs classification and its implication on hydrocarbon exploration: Cases studies from Tarim Basin.ActaPetrologicaSinica(in Chinese), 29(9): 3213-3222.

Zhu T, Li X F, Li Y Q, et al. 2011. Seismic scalar wave equation inversion based on an improved particle swarm optimization algorithm.ChineseJ.Geophys. (in Chinese), 54(11): 2951-2959, doi: 10.3969/jissn.0001-5733.2011.11.025.

附中文参考文献韩家炜, 坎伯. 2001. 数据挖掘: 概念与技术. 北京: 机械工业出版社. 李芳, 王守东, 陈小宏等. 2014. 基于模糊逻辑的多属性融合油气预测方法. 石油地球物理勘探, 49(1): 197-204.

刘靖明, 韩丽川, 侯立文. 2005. 基于粒子群的K均值聚类算法. 系统工程理论与实践, (6): 54-58.

刘力辉, 杨梦岩, 熊金良等. 1996. 应用自组织神经网络划分地震微相. 石油地球物理勘探, (S2): 90-94.

陆文凯, 牟永光. 1998. 用自组织神经网络实现地震同相轴自动追踪. 石油物探, 37(1): 77-83.

穆星. 2005. 利用地震几何属性和自组织神经网络进行地震相的自动识别. 地质科技情报, 24(3): 109-112.

岳碧波, 彭真明, 洪余刚等. 2009. 基于粒子群优化算法的叠前角道集子波反演. 地球物理学报, 52(12): 3116-3123, doi: 10.3969/j.issn.0001-5733.2009.12.021.

张学工. 2010. 模式识别(第三版). 北京: 清华大学出版社.

赵文智, 沈安江, 潘文庆等. 2013. 碳酸盐岩岩溶储层类型研究及对勘探的指导意义——以塔里木盆地岩溶储层为例. 岩石学报, 29(9): 3213-3222.

朱童, 李小凡, 李一琼等. 2011. 基于改进粒子群算法的地震标量波方程反演. 地球物理学报, 54(11): 2951-2959, doi: 10.3969/j.issn.0001-5733.2011.11.025.

(本文编辑 胡素芳)

Unsupervised seismic facies analysis technology based on SOM and PSO

ZHANG Yan1, ZHENG Xiao-Dong1, LI Jin-Song1, LU Jiao-Tong2, CAO Cheng-Yin1, SUI Jing-Kun1

1ResearchInstituteofPetroleumExploration&Development，Beijing100083，China2SinopecGeophysicalCorporation,Beijing100029,China

Seismic facies, as the mappable 3D seismic units composed of groups of reflections whose parameters differ from those of adjacent facies units, represent seismic reflections to macro characteristics of sedimentary facies. Seismic facies analysis technique is to describe and interpret the seismic reflection parameters, such as configuration, continuity, amplitude, and frequency, within the stratigraphic framework of a depositional sequence. As a key step in the seismic interpretation workflow, seismic facies analysis determines so much information on depositional process, environment and ultimately can predict potential reservoir only from seismic data in the absence of well data. When the geological information is incomplete or nonexistent, seismic facies analysis is called non-supervised and is performed through unsupervised learning or clustering algorithms. Although unsupervised seismic facies analysis is an effective technique for reservoir prediction, the big seismic data are processed slowly with the traditional methods.In order to overcome the defects of traditional ways which easily fall into the minimum value and lead to the inaccuracy of the cluster of seismic data, this paper proposes a new method to analyse seismic facies combining the Self-Organizing Map (SOM) and the Particle Swarm Optimization (PSO). In this paper, we firstly select the sensitive attribute which can reflect the geological target and normalize the seismic attribute and initialize the SOM network. The reason why we choose SOM is that it can compress a large number of redundant seismic data into a smaller number. As one of the most promising mathematical techniques applied to non-supervised pattern classification, SOM has the characteristics of keeping the topology structure of the original samples. Secondly we will train the seismic attribute one by one in the network, compute the distance between neuron and sample according to Euclidean distance, confirm the optimum matching unit, and update the weight according to renewing criterion. If it reaches to a certain iteration or the weight trends to stabilization, the training is finished, otherwise, return to last step. After the previous data compression, we will improve the K-means cluster using the global optimization of the PSO, which is initialized with a group of random particles (solutions) and then search for optima by updating generations. In every iteration, each particle is updated by following two “best” values. The first one is the best solution (fitness) it has achieved so far, which is called pbest displaying the best location. Another “best” value that is tracked by the particle swarm optimizer is the best value, obtained so far by any particle in the population, which is a global best and called gbest indicating the best swarm. Based on the well trained SOM network, we can find out a proper clustering divide using PSO optimizing method directly, which minimize the fitting degree from which we can get the minimum Euclidean distance then we record down the pbest and gbest. On the basis of results in the last step, we can update all the particles′ velocities and locations and cluster them again and keep a record of the corresponding relationship between attribute samples and neurons. If it reaches to the iterative condition, then quits the algorithm, otherwise, returns to last step to recompute them. Finally, we reverse mapping the clustering results into the original samples space to acquire the well classified attribute samples.In the theoretical model, we design a four layers medium model with a horizontal velocity change in the second layer which means the formation lithology variation in the lateral. With the Ricker wavelet forward modeling, we get the synthetic seismogram and then use the algorithm in the last paragraph mentioned to cluster them, which defaults the time samples as the attribute. Based on our method, three kinds of variations in the lateral can be clearly displayed, from which different colors represent the different classifications. Meanwhile, this method has a very good stability and convergence when the iteration times increase the objective function value still is near zero. For the purpose of testing the robustness to noise, we add noise of different Signal to Noise Ratio (SNR) to model, including SNR=25 dB, SNR=10 dB, SNR=2 dB and SNR<1 dB. From the results, we can find that when SNR>1 the clustering performance is very good and the horizontal variation is discriminated very well by the distinct boundaries. Even if SNR<1 we still can detect the changes basically, and the results can be referenced for our research although there are some clustering errors. Especially we select the SNR<1 models to be processed by certain commercial software from which the clustering is completely disordered and disappointing. It indicates that we can get stable results using our method when the seismic data quality is bad. According to the application to real data from Tarim Basin, the seismic facies map based on our method and SOM are better than the commercial software, the border and fault zone of reef facies are depicted more clearly. From comparing the seismic faices to the wells located in the area, we can find out that oil wells W2, W21, W22 and W23 are distributed in the red color area which implies the potential oil reservoir and dry wells W25 and W28 are located in the brown belt which doesn′t have oil production processed by our method. At the same time, our improved algorithm can greatly shorten the calculation time from comparison of consuming time between our algorithm and commercial software.The traditional seismic facies analysis methods are usually restricted by the massive seismic data because of very low computational efficiency. In our paper, we try to solve the problem and propose a new multi-attribute clustering method combining the SOM and PSO. We make full use of the SOM advantage of compressing redundant seismic data into a smaller number and keeping the original topology structure, and then improve the K-mean clustering by the PSO global optimizing characteristic. The theoretical model and real data show that our algorithm can realize the compression of the seismic data effectively, and provide a more accurate global solution. For seismic facies prediction, it does well in both the calculation efficiency and the accuracy.

Self-organizing feature map (SOM); Particle Swarm Optimization (PSO); Unsupervised seismic facies analysis; Clustering

10.6038/cjg20150933.

Zhang Y, Zheng X D, Li J S, et al. 2015. Unsupervised seismic facies analysis technology based on SOM and PSO.ChineseJ.Geophys. (in Chinese),58(9):3412-3423,doi:10.6038/cjg20150933.

10.6038/cjg20150933

P631

2014-06-11，2015-07-07收修定稿

国家重大专项(2011ZX05004-003)和国家自然科学基金(40504110)联合资助.

张，女，1990年生，中国石油勘探开发研究院在读博士研究生，主要从事地震储层预测方面的研究工作.E-mail:xiaoyan_zy@163.com