基于储层砂岩微观孔隙结构特征的弹性波频散响应分析

邓继新, 周浩, 王欢, 赵建国, 王尚旭

1 油气藏地质及开发工程国家重点实验室，成都理工大学, 成都 610059 2 成都理工大学地球物理学院地球物理与勘查技术系, 成都 610059 3 中国石油大学CNPC物探重点实验室, 北京 102249



基于储层砂岩微观孔隙结构特征的弹性波频散响应分析

邓继新1,2, 周浩2, 王欢2, 赵建国3, 王尚旭3

1 油气藏地质及开发工程国家重点实验室，成都理工大学, 成都 610059 2 成都理工大学地球物理学院地球物理与勘查技术系, 成都 610059 3 中国石油大学CNPC物探重点实验室, 北京 102249

储层砂岩微观孔隙结构特征不仅影响干燥岩石的弹性波传播速度,也决定了岩石介质中与流体流动相关的速度频散与衰减作用.依据储层砂岩微观结构特征及速度随有效压力变化的非线性特征,将其孔隙体系理想化为不同形状的硬孔隙(纵横比α>0.01)与软孔隙(纵横比α<0.01)的组合(双孔隙结构).基于孔弹性理论,给出软孔隙最小初始纵横比值(一定压力下所有未闭合软孔隙在零压力时的纵横比最小值)的解析表达式,并在此基础上利用岩石速度-压力实验观测结果给出求取介质中两类孔隙纵横比及其含量分布特征的方法.通过逐步迭代加入软孔隙的方法对基于特征纵横比的“喷射流”(squirt fluid)模型进行了扩展,以考虑复杂孔隙分布特征对岩石喷射流作用的影响及其可能引起的速度频散特征.相较于典型的喷射流作用速度频散模式,对于岩石中软孔隙纵横比及其对应含量在较宽的范围呈谱分布的一般情况, 其速度频散曲线不存在明显的低频段和中间频段,速度随频率的增大呈递增趋势直至高频极限.这说明即使在地震频段,微观尺度下的喷射流作用仍起一定作用,同样会造成流体饱和岩石介质的地震速度与Gassmann方程预测结果有不可忽略的差异.本文是对现有喷射流模型的重要补充,也为利用实验数据建立不同频段间岩石弹性波传播速度的可能联系提供了理论依据.

储层砂岩； 孔隙结构； 喷射流作用； 速度频散

1 引言

岩石弹性波传播速度作为联系岩石物性性质及其地震响应的有效桥梁一直是地球物理相关研究的重要内容.由于影响速度的因素众多,针对岩石中弹性波速度的研究涉及面也较为广泛.一般而言,岩石的弹性波速度是由岩石的矿物组分特征、孔隙流体性质、孔隙度和孔隙结构特征等因素决定(陈颙和黄庭芳,2001).在这些影响因素中,孔隙度与孔隙结构的综合影响对岩石的速度变化特征起主要作用，同时也决定了岩石中与流体流动相关的速度频散与衰减作用.

对干燥岩石而言,主要通过微分等效模型(DEM)、自洽模型(SCA)等来定量表征孔隙度与孔隙微观结构对弹性波速度的影响(O′Connell and Budiansky,1974; Norris,1985).以具有不同纵横比值的椭球体来表示孔隙结构特征的变化,均以Eshelby(1957)的单一椭球体等效夹杂理论为基础.流体饱和条件下,由于孔隙形状差异引起了孔隙弹性性质的差异,在弹性波的作用下这种微观尺度上孔隙弹性特征差异会诱发不同孔隙间的流体流动作用,即“喷射流”作用,从而引发弹性波的速度频散和衰减.描述喷射流作用的理论模型可分为两类,其一是首先将岩石中不同形状的孔隙理想化为“软”孔隙(在相同有效压力下容易被压缩,主要表现为颗粒接触边界和微裂隙)和“硬”孔隙两种类型的孔隙,两类孔隙间流体流动满足Navier-Stokes流动方程,然后通过表征不同频率下孔隙间流体流动作用对软孔隙刚度的改变来描述喷射流作用对岩石整体性质的影响,该类模型以Murphy等(1986)和Mavko和Jizba(1991)的微观颗粒尺度流体松弛机制以及Dvorkin和Nur(1993)和Dvorkin等(1995)所给出的BISQ(BIot-Squirt)理论模型为代表;其二是以无限大均匀介质中单一椭球体的弹性响应为基础的夹杂体模型(Inclusion-based model),利用孔隙流体质量守恒及Darcy定理描述不同孔隙形状的孔隙间的流体流动作用,例如Hudson等(1996)给出的含裂隙孔隙介质喷射流模型,以及Jakobsen等(2003)和Jakobsen和Chapman(2009)基于T-矩阵方法所给出的考虑宏观流体流动和微观喷射流动的统一理论模型.在这些基础上,杨顶辉等国内学者(Yang and Zhang,2002; Cheng et al.,2002; Yang et al.,2014)较为系统深入地研究了含流体孔隙介质中的BISQ 模型,将BISQ 理论推广到了一般的孔隙各向异性情况,并就各向异性介质中的 BISQ 模型进行了详细的理论分析和数值模拟实验,拓展了 BISQ 理论的应用范围.聂建新等(Nie and Yang, 2008；Nie et al.,2012)则提出了含流体非饱和黏弹性孔隙介质中的 BISQ 模型,通过与弹性BISQ 模型的预测结果、实验数据等的比较表明:在一定情况下,波的黏弹性衰减机理不可忽视.在夹杂体模型中虽然包含了孔隙结构参数如纵横比等信息,但由于模型过于复杂而很难应用;同时该类模型在低频极限条件下与Gassmann方程结果不一致.BISQ理论模型利用特征喷射流长度等唯象参数来表征微观孔隙尺度上的不均匀性,不能较为直接地反映岩石自身孔隙特征变化对弹性波传播特征的影响.鉴于这些不足之处,Gurevich等(2010)和Tang(2011)基于相同的孔隙结构模型,采用不同的方法给出了弹性波传播特征与岩石孔隙结构特征(纵横比、软孔隙含量和微裂隙密度)的理论关系.

在Gurevich等(2010)和Tang(2011)两种喷射流模型中,软孔隙都是起决定性作用的, 岩石速度频散的强度和特征频率均主要由岩石的软孔隙决定. 虽然Gurevich等(2010)和Tang(2011)的文章中给出了孔隙介质的弹性模量与孔隙结构特征的关系,但文中仅给出含某一特定纵横比及含量的软孔隙对岩石速度频散与衰减的影响.在实际的储层岩石中,软孔隙的纵横比值往往不是一个定值,而应该是对应于一个连续的分布范围.对于具有一定孔隙连续分布特征的实际岩石而言,其频散和衰减特征并无更多的讨论.正是基于这个问题,本文利用干燥岩石压力-速度数据求取岩石的孔隙分布特征,并在此基础上结合孔隙尺度喷射流作用机制,给出了具有复杂孔隙分布特征的岩石所表现出的可能的速度频散及衰减特征,为更准确评价复杂岩石介质的弹性波传播特征提供理论依据.

2 储层砂岩微观孔隙结构特征

孔隙结构是指岩石所具有的孔隙和喉道的几何形状、大小、分布及其相互连通关系.孔隙大小主要影响储层的孔隙度,喉道大小与连通状况直接影响着岩石的渗透性等物性特征.从力学的角度看来,岩石的孔隙,包括原生粒间孔及溶蚀孔隙,可视为不易压缩的硬孔隙,其纵横比α>0.01;孔喉,包括颗粒接触边界、孔隙边界的封闭角落以及一些文献中统称的微裂隙(图1a),则可视为易压缩的软孔隙,其纵横比α<0.01.成岩过程对孔隙结构的演化起决定性作用,成岩早期骨架颗粒间主要为点接触或点-线接触,岩石中的孔隙形状具有明显的多凹面形态,这种形状的孔隙可等效为硬孔隙与多个软孔隙的组合(图1b);当压实作用进一步加强(包括化学压实作用),颗粒排列将更加紧密,颗粒之间逐渐呈线接触关系,两颗粒之间由微细孔隙组成的通道形成数量较多的微细孔隙,在某种程度上这些微细孔隙本身就是软孔隙, 残余粒间孔隙的形状也逐步演变为三角形或者长方形(图1a).

图1 砂岩孔隙结构特征(a) 须家河组致密砂岩(φ=5.3%)； (b) 黄流组常规砂岩(φ=13.1%).Fig.1 Pore structure of reservoir sandstone shown by thin-section photomicrographs(a) Thin section of tight sandstone from Xujiahe Formation; (b) Thin section of common sandstone from Huangliu Formation.

不难发现,砂岩的孔隙体系总能理想化为不同形状的硬孔隙与软孔隙的组合.基质中任意类型孔隙的加入都会改变岩石介质的等效刚度或者等效柔度. 从静力学的角度看,孔隙的加入形成附加应变从而改变岩石的等效柔度在物理意义上更为明确.因此,在表征孔隙度及孔隙形状对岩石弹性性质影响时,采用等效柔度表示方法相较于等效刚度表示方法也通常更准确,尤其是对于孔隙或裂隙等软孔隙含量较高的情况.假定岩石基质的柔度为S0,硬孔隙与软孔隙的加入所产生的附加柔度分别为ΔSsoft与ΔSstiff,则岩石等效柔度S可表示为

S=S0+ΔSsoft+ΔSstiff.

(1)

由于附加柔度的线性叠加性,在具有双孔结构特征的砂岩基质中添加孔隙可以分成两个阶段. 首先将硬孔隙加入基质中,如果考虑孔隙间的相互作用,岩石介质的等效弹性模量(Kstiff、μstiff)按其柔度形式可用Mori-Tanaka公式计算(Mori and Tanaka,1973)，表达式为

(2)

其中K0、μ0分别为岩石基质组成颗粒的体积与剪切模量,φs为硬孔隙的孔隙度,P、Q分别为归一化孔隙可压缩系数与剪切柔度, 为基质弹性模量与孔隙纵横比α的函数.实际上P、Q也可理解为硬孔隙的形状因子,对于球形孔隙等规则形状孔隙P、Q可得到解析解;对于不规则孔隙可通过对弹性模量或速度的测量结果进行拟合得到. 在此基础上再加入软孔隙, 此时基质等效体积与剪切模量分别为(Kstiff、μstiff), 岩石介质的等效弹性模量(Kd、μd)按其柔度形式仍然可用Mori-Tanaka公式计算，表达式为

(3)

式中φc为软孔隙的孔隙度,P、Q为软孔隙形状因子.如果将软孔隙看作微裂隙, 在裂隙纵横比小于0.1～0.2的情况下, 裂隙自身的柔度与裂隙纵横比无关, 而更多地取决于裂隙密度ε(Kachanov et al.,1994), 因此在考虑软孔隙影响时可利用裂隙密度代替其孔隙度, 两者关系为(David and Zimmerman, 2012)

φc.

(4)

岩石中裂隙的形状极为复杂, 而形状又对其柔度有明显的影响, 为使后续计算简化, 采用简单类球体模型代替软孔隙形状,P、Q可给出解析表达式(Zimmerman,1986;Kachanov et al.,1994). 同时由于岩石中软孔隙φc很小, 此时公式(3)可表示为

(5)

式中υstiff为岩石仅含硬孔隙的泊松比,ε表示岩石中所有未闭合软孔隙的累积裂隙密度. 由于硬孔隙随压力变化较小, 仅含该类孔隙的岩石的等效弹性模量与高有效压力下的弹性模量(Kh、μh)近似,而(Kh、μh)则可通过干燥岩石速度-有效压力实验曲线得到, 如选择该曲线线性段反向延长与纵轴的交点所给出的速度值, 也可直接选择高有效压力的速度值(Gurevichetal.,2010). 采用Kh、μh分别代替Kstiff与μstiff可避免讨论硬孔隙形状因子P、Q的影响, 而直接利用公式(5)求取软孔隙特征.

3 孔隙分布特征计算

3.1 孔隙分布计算方法

对单一孔隙/裂隙，其闭合压力p与纵横比α近似满足关系:p=αE0, 其中E0为基质颗粒杨氏模量.成分主要为石英颗粒的砂岩的杨氏模量为80GPa, 那么纵横比α=0.01的孔隙闭合的压力应为800 MPa左右,这个压力远大于通常的实验压力. 因此可将α=0.01作为软孔隙与硬孔隙的分界. 已有研究结果表明, 干燥岩石的速度通常会随着压力的增大而逐渐增大,这种变化趋势主要是由于岩石中的软孔隙在压力增大的过程中,先后闭合而引起的;而不可闭合孔隙(硬孔隙)对岩石的速度-压力变化关系几乎不做贡献, 其纵横比随压力表现出非常微小变化(陈颙和黄庭芳,2001;Shapiro,2003；David and Zimmerman,2012). 基于上述分析, 硬孔隙对岩石等效柔度公式(2)的改变是压力无关的, 而软孔隙对等效柔度公式(5)的改变是压力相关的. 换句话说, 每个有效压力下的速度对应着特定纵横比的软孔隙闭合, 这也是利用速度-压力变化关系计算软孔隙分布的基础.

确定岩石的孔隙结构就是要给出硬孔隙和软孔隙纵横比的分布及其对应的孔隙含量. 由于硬孔隙对岩石等效弹性性质的影响较为简单, 同时不表现出明显的压力相关性, 造成很难直接利用速度-有效压力关系曲线直接求取纵横比分布及其含量. 本文采用单一纵横比来表征硬孔隙的平均特征. 具体计算方法是根据速度-有效压力曲线确定Kh、μh,再利用公式(2)求取与之最贴合的Kstiff与μstiff以及相应的硬孔隙纵横比.

在得到硬孔隙的平均纵横比后, 确定岩石孔隙结构则主要是确定其中软孔隙的纵横比及对应含量的可能分布特征.David和Zimmerman(2012)给出了有效压力p下未闭合的所有软孔隙的最小初始纵横比值αi的计算公式为

(6)

式中εp表示有效压力p下未闭合软孔隙的累积裂隙密度,ε0表示零有效压下岩石中的初始裂隙密度,Kd(εp)表示岩石在有效压力p下的体积模量.

在假定软孔隙的孔隙形状为类球形时,Kd(εp)可用公式(5)计算.研究表明,干燥岩石中的软孔隙裂隙密度随有效压力的增大一般呈指数递减趋势(Shapiro, 2003).可假设不同有效压力下的裂隙密度εp与零压下的初始裂隙密度ε0满足指数关系为

(7)

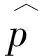
(8)

结合公式(5)和公式(8)可给出αi在Mori-Tanaka模型下的解析表达式为

(9)

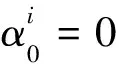
值得一提的是,将公式(7)再代入(9)中可得:

(10)

不难发现公式(10)就是p=αE0的另一种表达形式.但从物理意义看来,p=αE0中的α表示的是单一裂隙岩石模型中孔隙的纵横比值,而αi表达的是含裂隙分布岩石中未闭合软孔隙的最小初始纵横比,两者所对应的岩石孔隙结构类型是完全不同的;除此之外,p=αE0中的E0是岩石基质的杨氏模量,而Eh,mt则是含未闭合硬孔隙岩石的杨氏模量.

利用上述方法,我们可以由干燥岩石的速度-压力曲线提取出岩石的孔隙分布特征,但要注意的是,这个孔隙分布特征实际上是有效压力为零时岩石的孔隙分布特征.Zimmerman(1991)指出,在压力逐渐增大的过程中,岩石中各纵横比的软孔隙的纵横比的减小量应该是一致的,并且所有软孔隙的纵横比值与压力的关系为

′.

(11)

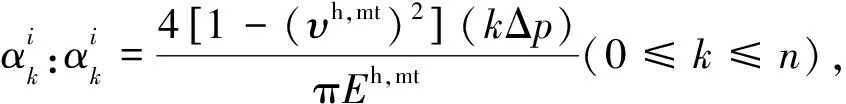
3.2 实际岩石的孔隙分布特征

图2中给出不同有效压力下两块储层砂岩样品分别在干燥和饱水条件下的纵、横波速度测量结果, 测量方法为标准的超声波脉冲传输法, 配套宽频带纵波PZT换能器的主频为700 kHz,横波为350 kHz. 两块岩石样品均未见手标本尺度上的不均匀性(包括可见裂隙), TS1样品取川东北的须家河致密砂岩储层, S1样品取自南海黄流组常规砂岩储层. XRD分析表明TS1样品主要矿物组分为石英、长石与后期胶结物方解石, 方解石含量为22.8%, 黏土含量为0.4%; S1样品主要矿物组分石英、长石与少量黏土, 黏土含量为12%. TS1与S1样品孔隙度分别为5.5%与13.1%, 岩石孔隙结构特征见图1.

由图2知,纵横波速度均表现出相同的变化方式, 在有效压力小于30 MPa时, 速度随有效压力的增大迅速增大, 压力-速度变化关系曲线呈明显非线性特征; 大于该有效压力时, 压力-速度变化关系近于线性, 同时速度随着压力的增大变缓. 压力-速度变化曲线的非线性部分通常被认为是由岩石中纵横比较小的软孔隙在压力增大的过程中先后闭合引起的, 而线性段则是纵横比较大的硬孔隙的响应.本文以最大压力处的速度作为高压速度,采用前面一节提出的硬孔隙计算方法, 求得TS1样品与S1样品硬孔隙纵横比分别为0.1与0.21.从纵横比看硬孔隙的形状更接近于扁圆椭球体而非球体.在计算过程中, 样品基质组成颗粒模量(K0、G0)是通过Voigt-Reuss-Hill平均公式计算,TS1样品基质组成颗粒的体积与剪切模量分别为43.9GPa与32.5GPa,S1样品的分别为34.5GPa与26.4GPa.

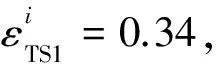
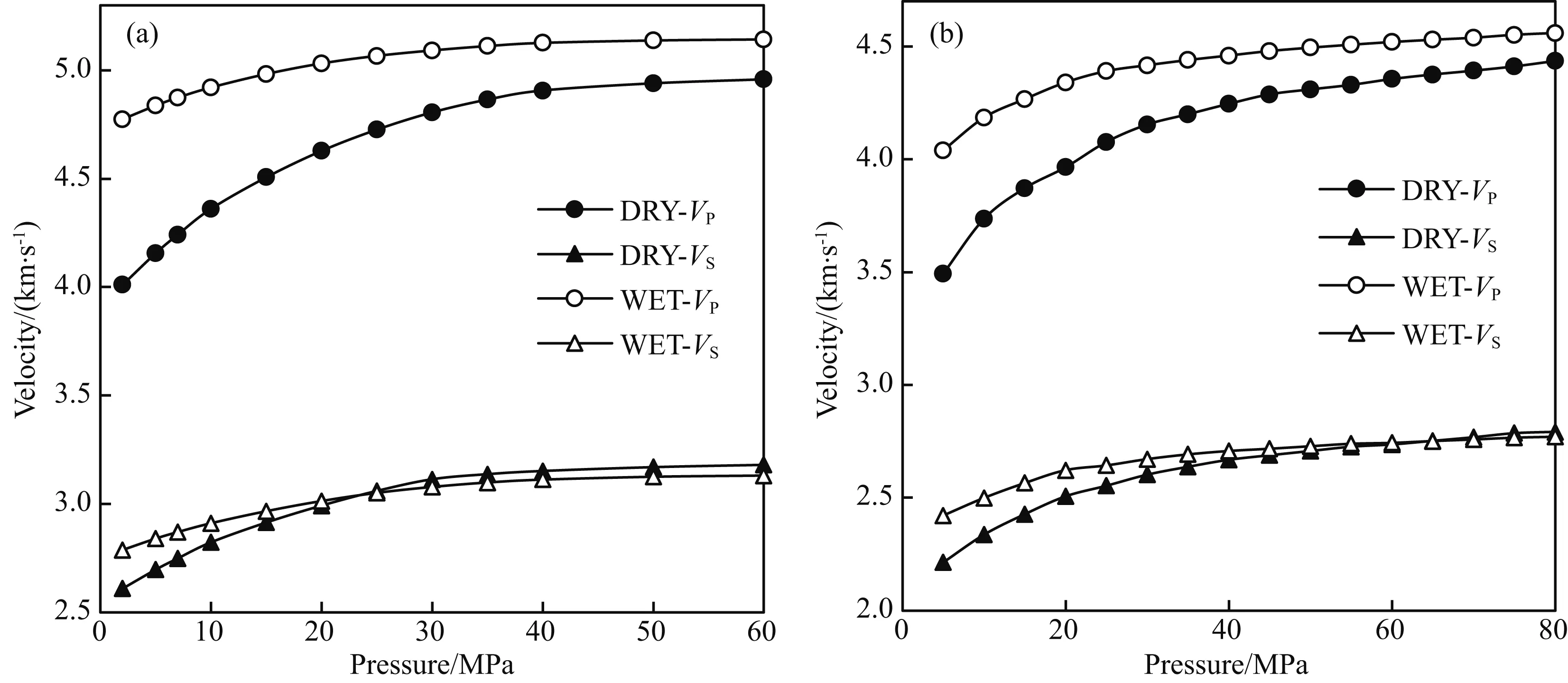
图2 饱水和干燥岩石的压力-速度曲线(a) 致密砂岩TS1的压力-纵横波速度曲线; (b) 常规砂岩S1的压力-纵横波速度曲线.Fig.2 Velocity versus confining pressure of dry and saturated rocks(a) Velocity-pressure curve of compact sandstone sample TS1; (b) Velocity-pressure curve of common sandstone sample S1

隙度的0.69%.致密砂岩TS1的软孔隙的初始裂隙密度和总孔隙度都小于S1的,并且TS1的总孔隙度也约为S1的二分之一,因此TS1在纵、横波速度上整体比S1的速度大.一般而言,如果纵横比的分布范围更广,那么在压力逐渐增大的过程中,几乎在各个压力点都有一定量软孔隙闭合,因而速度随着压力增大的趋势较平缓,即可能在整个压力变化范围内速度随压力增大呈线性增加趋势;相反,如果软孔隙分布范围更窄,即在某个局部压力范围内会有大量软孔隙闭合,造成速度在该局部压力区间内变化较快,而在其余压力范围内变化平缓,形成典型的压力-速度的非线性变化趋势.由图3和图4可知,虽然TS1和S1的孔隙分布形态相似,但是砂岩TS1在各纵横比的软孔隙的孔隙度和裂隙密度都相对更小,因此TS1砂岩的速度曲线变化相对更为平缓.

4 基于孔隙结构的喷射流作用

4.1 基于孔隙结构的喷射流模型

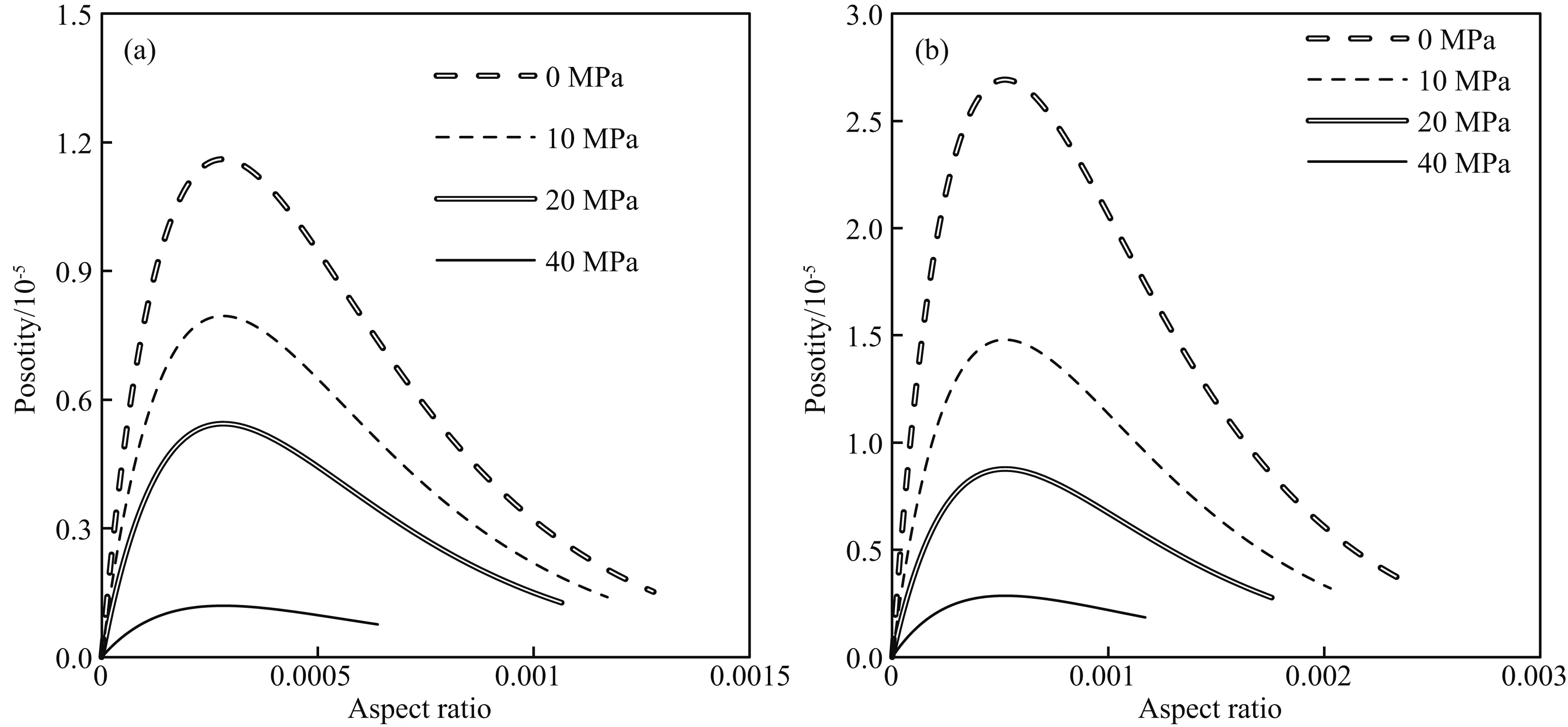
图3 TS1致密砂岩样品(a)与S1常规砂岩(b)软孔隙纵横比的孔隙度分布特征Fig.3 Porosity distribution as function of aspect ratio of soft pore for TS1 compact sandstone sample (a) and S1 common sandstone sample (b)

图4 TS1致密砂岩样品(a)与S1常规砂岩(b)软孔隙累积裂隙密度分布Fig.4 Cumulative crack density distribution as function of aspect ratio of soft pore for TS1 compact sandstone sample (a) and S1 common sandstone sample (b)

在微观孔隙尺度下流体流动作用对岩石弹性性质的影响可用喷射流理论描述. 对具有双孔孔隙结构的岩石而言,弹性波的频散和衰减主要是由岩石中的软孔隙决定.在众多的喷射流理论表述中, Tang(2011)给出了岩石介质中微裂隙与孔隙并存的弹性波统一理论, 并将喷射流作用同岩石中微裂隙(软孔隙)裂隙密度ε以及纵横比α这两个重要孔隙结构参数建立了联系. 利用相同的孔隙结构模型,Gurevich等(2010)将喷射流作用同岩石中微裂隙孔隙度φc以及纵横比α联系起来. 在Gurevich等(2010)的方法中延续了Murphy等(1986)与Dvorkin等(1995)的思想, 考虑了软孔隙中流体弛豫作用对其柔度的影响.如果将仅含干燥硬孔隙的岩石作为新的等效基质, 其体积模量为Kstiff(通常用Kh替代), 加入软孔隙并考虑软孔隙与硬孔隙中流体喷射流作用影响时, 岩石等效模量Kmf、μmf的计算公式为

(12)

式中ω为圆频率,η为孔隙流体动态黏度,αc为软孔隙特征纵横比,φc(p)为一定有效压力p下的软孔隙孔隙度,Kd(p)、μd(p)分别为有效压力p下岩石中含有纵横比为αc、孔隙度为φc(p)的软孔隙时的干燥体积与剪切模量.

公式(12)右端第二项可理解为在Kh的基础上,通过加入特定纵横比的饱和流体软孔隙来表征喷射流作用.在考虑软孔隙作用后,剩余硬孔隙因其不可压缩性,在流体饱和后仍满足Gassmann方程, 此时硬孔隙完全饱和时的体积模量Ksat与剪切模量μsat的计算公式为

μsat(p,ω)=μmf(p,ω).

(13)

实际岩石中的软孔隙的纵横比不可能为一个固定值,而是在一定的范围内呈连续分布的. 因此,研究孔隙具有一定分布特征的岩石所具有的喷射流频散和衰减作用则更为必要.在得到岩石中软孔隙纵横比值关于孔隙度的分布数据后, 如果将其离散, 则对每个离散后的孔隙纵横比和对应孔隙度可仍然采用公式(12)的方法计算软孔隙喷射流作用的影响. 然后通过迭代加入各纵横比的软孔隙计算基于孔隙分布的岩石的Kmf和μmf.在迭代加入软孔隙的过程中,除首次加入软孔隙以公式(12)计算外, 第k次加入软孔隙所计算的Kmf和μmf值,将视作第(k+1)次加入软孔隙的Kh和μh;而在Kh和μh基础上加入软孔隙即得第(k+1)次的Kd和μd.整个加入软孔隙的过程可表述为

(14)

将所得到Kmf和μmf再分别代入公式(13)中计算硬孔隙完全饱和时的体积模量Ksat与剪切模量μsat.因为公式(12)实质是弹性模量的柔度形式,这种逐步添加软孔隙的方法具有合理性,并且软孔隙不论是按照纵横比增大的顺序添加还是按相反的顺序添加其计算结果均相同.

4.2 模型计算结果分析

以TS1与S1两块砂岩为例,在得到其孔隙纵横比值的孔隙度分布特征的基础上(图3和图4),利用4.1小节中所给出的方法可以做出全频段内基于孔隙分布的岩石的总体纵、横波速度频散曲线(图5和图6). 作为对比,图中同时给出了将各纵横比值对应的软孔隙按其孔隙度通过公式(12)计算的各条仅含单一纵横比软孔隙的岩石的纵、横波速度频散曲线. 图中红色曲线对应着基于孔隙分布的岩石的综合速度频散曲线,对应左侧纵坐标轴; 而蓝色曲线则对应于各特定纵横比软孔隙的速度频散曲线,对应右侧纵坐标轴.综合速度频散曲线与各特定纵横比速度频散曲线在形态具有较大的差异,基于岩石孔隙分布的综合频散曲线从1 Hz到高频极限处纵、横波速度均呈逐渐增大趋势,速度频散曲线没有明显的低频段(弹性波诱发孔压在不同孔隙间达到平衡)和中间频段;当频率低于高频界限时,曲线形态大致为各单一纵横比频散曲线中间段的包络,岩石中弹性波的总频散可视为各纵横比软孔隙频散作用的综合累积效应.通常认为,在流体黏度较低的情况下,喷射流作用在测井频段或者更高的超声频段起作用(Pride and Berryman, 2003；Pride et al.,2004;邓继新等,2012).通过本文的分析可以看出,考虑岩石软孔隙实际分布特征,即使在地震频段其速度值也可能与Gassmann方程结果有不可忽略的差异.

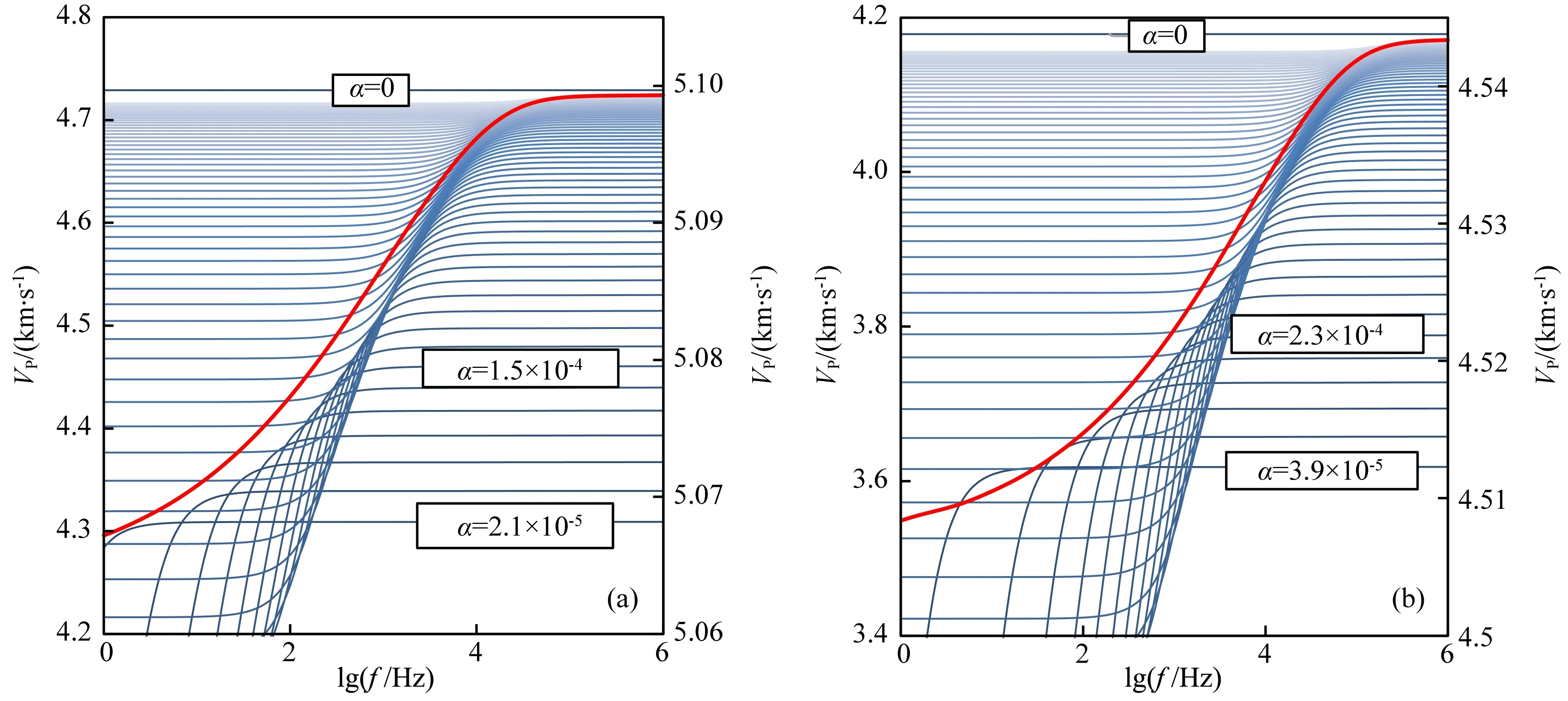
图5 基于孔隙分布的纵波速度频散与基于单纵横比模型的纵波速度频散关系(a) TS1致密砂岩样品纵波速度频散特征; (b) S1常规砂岩纵波速度频散特征.Fig.5 P-wave velocity dispersion calculated from pore distribution model and from single aspect ratio model(a) Dispersion for TS1 tight sandstone sample; (b) Dispersion for S1 normal sandstone sample.

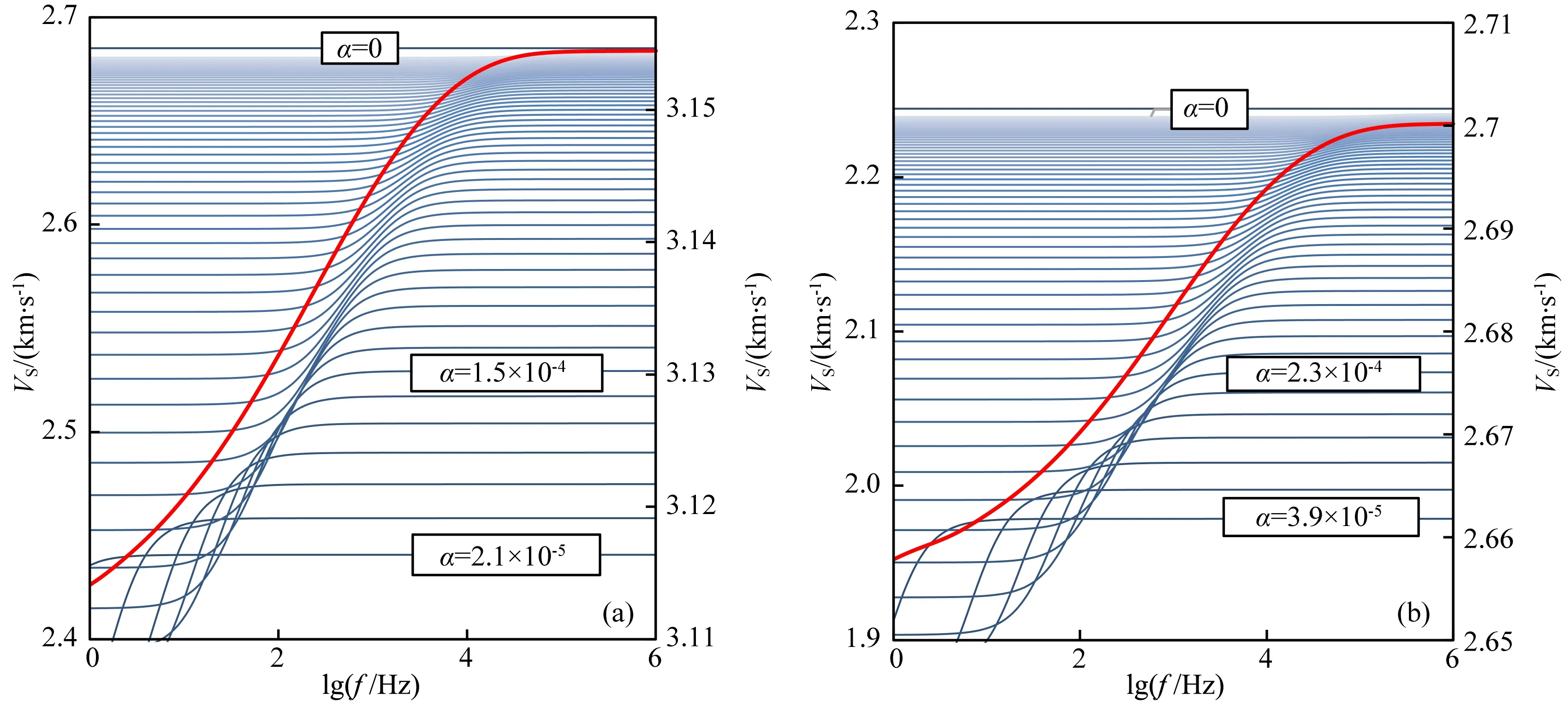
图6 基于孔隙分布的横波速度频散与基于单纵横比模型的横波速度频散关系(a) TS1致密砂岩样品横波速度频散特征; (b) S1常规砂岩横波速度频散特征.Fig.6 S-wave velocity dispersion calculated from pore distribution model and from single aspect ratio model(a) Dispersion for TS1 tight sandstone sample; (b) Dispersion for S1 common sandstone sample.

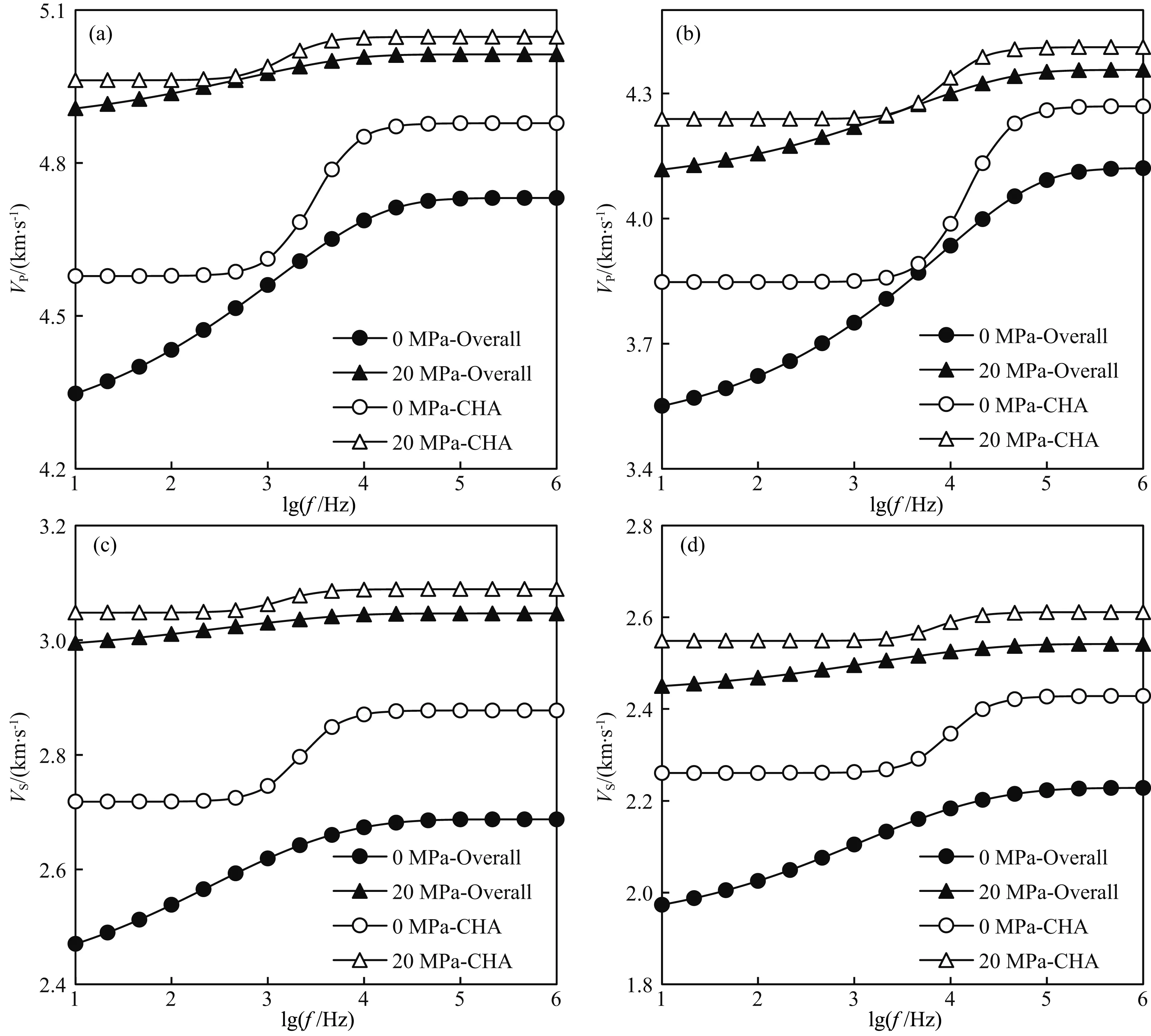
图7 基于孔隙分布和基于特征纵横比的速度频散特征对比(a) 致密砂岩TS1在0 MPa和20 MPa下纵波速度频散; (b) 常规砂岩S1在0 MPa和20 MPa下纵波速度频散; (c) 致密砂岩TS1在0 MPa和20 MPa下横波速度频散;(d) 常规砂岩S1在0 MPa和20 MPa下横波速度频散.Fig.7 Velocity dispersion calculated from pore distribution model and from characteristic aspect ratio model(a) and (b) P-wave velocity dispersion at confining pressure of 0 MPa and 20 MPa for sample TS1 and S1, respectively; (c)and (d) S-wave velocity dispersion at confining pressure of 0 MPa and 20 MPa for sample TS1 and S1, respectively.

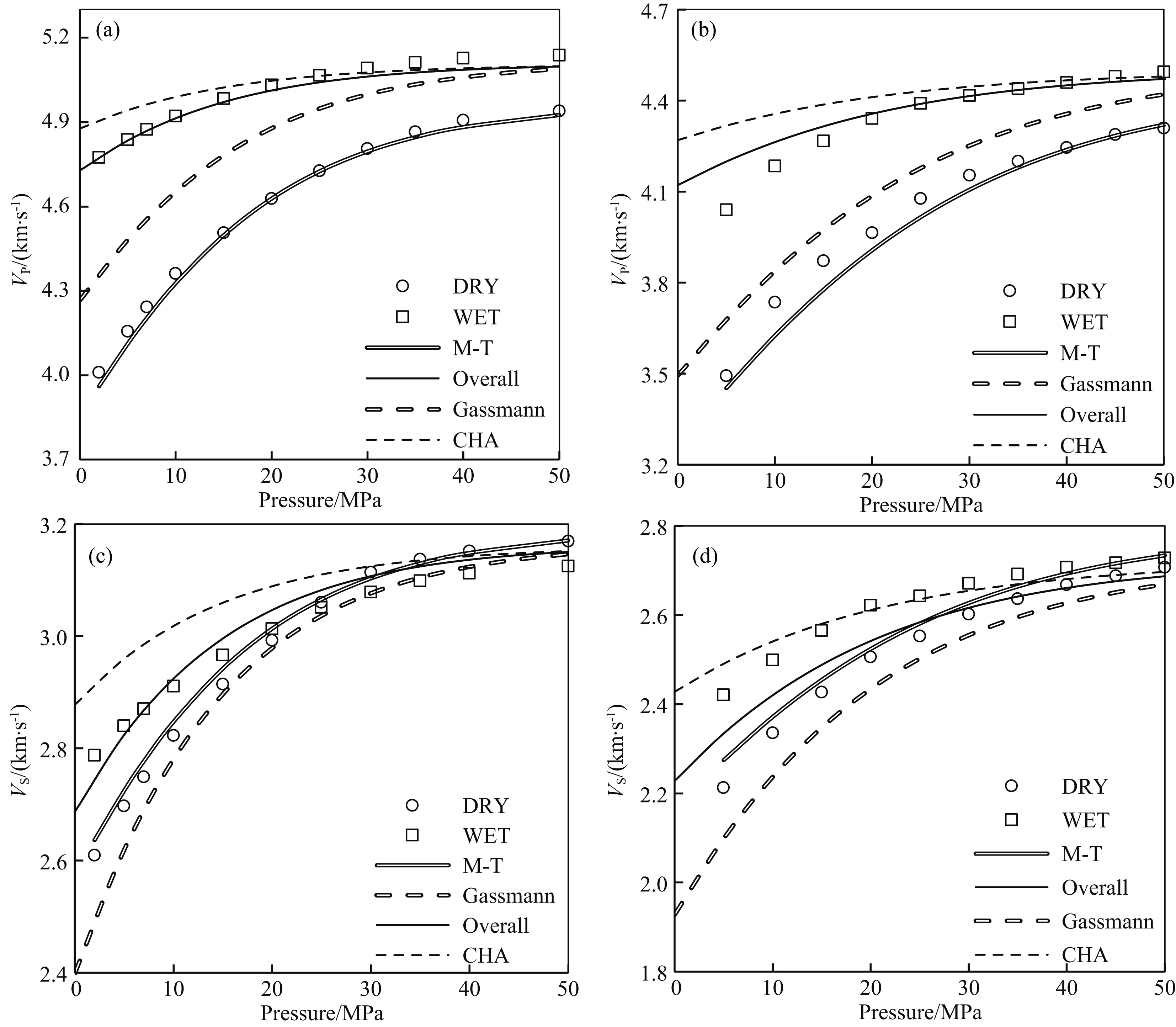
图8 不同围限压力下样品速度测量结果与模型计算结果对比(a) 致密砂岩TS1纵波速度实验结果与模型结果对比; (b) 常规砂岩S1纵波速度实验结果与模型结果对比; (c) 致密砂岩TS1的横波速度实验结果与模型结果对比; (d) 常规砂岩S1的横波速度实验结果与模型结果对比.Fig.8 Velocity measurement data and model prediction results as function of confining pressure at dry and water saturated conditions(a) Measured P-wave velocity and model prediction data for sample TS1; (b) Measured P-wave velocity and model prediction data for sample S1; (c) Measured S-wave velocity and model prediction data for sample TS1; (d) Measured S-wave velocity and model prediction data for sample S1.

现有文献中在描述岩石中软孔隙相关的喷射流作用时通常是用具有特定纵横比软孔隙的模型,这种模型可在某种程度上视作实际岩石介质中软孔隙分布的一种平均,在这里称为特征纵横比软孔隙模型.为比较不同压力下基于特征纵横比与基于孔隙分布的岩石介质速度频散曲线的差异,分别做出两种模型下岩石在0 MPa和20 MPa下岩石的纵、横波速度频散曲线(图7)，图中“Overall”为基于孔隙分布模型的速度频散计算结果; “CHA”为基于特征纵横比的速度频散计算结果，计算时取各个压力下基于软孔隙分布的一个加权平均纵横比来表征特征纵横比αcha，公式为

(15)

在基于特征纵横比与基于孔隙分布的两种模型中,不同压力下岩石的软孔隙总含量相同,并且随着压力的增大,不论是基于孔隙分布还是基于特征纵横比的速度频散强度均会减弱.这主要是由于岩石的速度频散强度主要由软孔隙含量决定,两种孔隙模型下软孔隙含量都会随压力的增大而减少.速度频散曲线的特征频率由软孔隙的纵横比值决定, 而软孔隙纵横比都会随压力的增大而减小,因此整个频散曲线高频界也会向低频方向移动; 由于基于孔隙分布的模型中纵横比变化为一较宽的范围, 造成其速度频散曲线不会像基于特征纵横比模型的速度频散曲线一样随着压力的增大而“迅速”向低频方向移动.对于某一固定压力下的速度频散曲线而言, 基于特征纵横比孔隙模型的速度频散曲线的高频界限、低频界限以及中间频段明显; 基于孔隙分布的速度频散曲线高频界限明显,无明显的低频界限和中间频段. 如果特征纵横比值的计算方法不同, 则频散的强度和特征频率都会随之变化, 但是频散曲线的“低频+中间频段+高频”的曲线形态是不会改变的,而这正是两种孔隙模型岩石速度频散曲线最明显的区别.

为了进一步验证基于孔隙分布的速度频散模型的适用性,我们将TS1号和S1号岩石在700KHz频率下测量的饱和岩石的速度与基于孔隙分布和基于特征纵横比的两种模型的理论计算结果进行了对比(图8).图中DRY表示岩石干燥测量速度值,WET表示水饱和速度测量值,M-T是以公式(5)结合各个压力下的孔隙分布数据计算的干燥压力-速度曲线,Gassmann是M-T对应的零频饱和流体压力-速度曲线,Overall为基于孔隙分布模型的高频饱和速度曲线,CHA为基于特征纵横比模型的高频饱和速度曲线.不难发现,以M-T计算的模型数据与实际测量数据是吻合得很好的,并且基于孔隙分布模型的饱和岩石压力-速度曲线相对于基于特征纵横比模型的压力-速度曲线而言,与实际高频速度测量结果符合得更好.除此之外,由于利用基于孔隙分布速度频散模型可以计算出任意压力下全频段内饱和流体岩石的纵横波速度,该频散模型在取频率为零时将与图8中的Gassmann曲线重合,在高频(f=100 kHz)时将与基于孔隙分布的Mavko和Jizba(1991)的高频模型(基于孔隙分布计算干燥体积和剪切模量)一致, 即与Overall曲线重合, 这证明了基于孔隙分布弹性波速度频散模型的正确性.

5 结论

基于孔弹性理论,采用简单类球体模型代替软孔隙(纵横比α<0.01)形状推导出软孔隙最小初始纵横比值的解析表示式,并在此基础上给出求取介质中孔隙分布特征(软孔隙纵横比及其对应含量的分布, 硬孔隙平均纵横比及其含量)的方法; 利用该方法针对实验砂岩样品所得的软、硬孔隙分布特征能够准确解释其速度随有效压力变化的非线性特征.

在得到岩石介质中孔隙分布特征的基础上,对基于特征纵横比的喷射流模型进行了扩展,以考虑岩石中软孔隙纵横比及其对应含量具有谱分布的情况下喷射流作用所引起的速度频散. 模型结果表明, 基于孔隙分布的速度频散曲线高频界限明显,频散曲线从1 Hz到高频界限处纵、横波速度呈逐渐增大趋势,即无明显的低频和中间频段; 而基于特征纵横比的喷射流模型, 其频散曲线具有典型的“低频+中间频段+高频”的曲线形态.上述结果说明,考虑岩石介质孔隙尤其是软孔隙实际分布特征,喷射流作用在地震频段仍可对弹性波速度有一定的影响,并造成其与Gassmann方程结果有不可忽略的差异.

Chen Y, Huang T F. 2001. Rock Physics (in Chinese). Beijing: Peking University Press.

Cheng Y F, Yang D H, Yang H Z. 2002. Biot/squirt model in viscoelastic porous media.ChinesePhysicsLetters, 19(3):445-448.

David E C, Zimmerman R W. 2012. Pore structure model for elastic wave velocities in fluid-saturated sandstones.J.Geophys.Res.,117(B7): B07210.

Deng J X, Wang S X, Du W. 2012. A study of the influence of mesoscopic pore fluid flow on the propagation properties of compressional wave—a case of periodic layered porous media.ChineseJ.Goephys.(in Chinese), 55(8): 2716-2727, doi: 10.6038/j.issn.0001-5733.2012.08.024.

Dvorkin J, Mavko G, Nur A. 1995. Squirt flow in fully saturated rocks.Geophysics, 60(1): 97-107.

Dvorkin J, Nur A. 1993.Dynamic poroelasticity: a unified model with the Squirt and the Biot mechanisms.Geophysics, 58(4): 524-533.

Eshelby J D. 1957.The determination of the elastic field of an ellipsoidal inclusion, and related problems.ProceedingsoftheRoyalSocietyofLondon.SeriesA,MathematicalandPhysicalSciences, 241(1226): 376-396. Gurevich B, MakarynskaD, de Paula O B, et al. 2010.A simple model for squirt-flow dispersion and attenuation in fluid-saturated granular rocks.Geophysics, 75(6): N109-N120.

Hudson J A, Liu E, Crampin S. 1996.The mechanical properties of materials with interconnected cracks and pores.GeophysicalJournalInternational, 124(1): 105-112.

Jakobsen M, Chapman M. 2009.Unified theory of global flow and squirt flow in cracked porous media.Geophysics, 74(2): WA65-WA76.

Jakobsen M, Johansen T A, McCann C. 2003.The acoustic signature of fluid flow in complex porous media.JournalofAppliedGeophysics, 54(3-4): 219-246.

Kachanov M, TsukrovI, Shafiro B. 1994. Effective moduli of solids with cavities of various shapes.AppliedMechanicsReviews, 47(1S): S151-S174.

Mavko G, Jizba A. 1991.Estimating grain-scale fluid effects on velocity dispersion in rocks.Geophysics, 56(12): 1940-1949.

Mori T, Tanaka K. 1973.Average stress in matrix and average elastic energy of materials with misfitting inclusions.ActaMater.,21(5): 571-574.

Murphy W F, Winkler K W, Kleinberg R L. 1986. Acoustic relaxation in sedimentary rocks: Dependence on grain contacts and fluid saturation.Geophysics, 51(3): 757-766.

Nie J X, Ba J, Yang D H, et al. 2012.BISQ model based on a Kelvin-Voigt viscoelastic frame in a partially saturated porous medium.AppliedGeophysics, 9(2): 213-222.

Nie J X, Yang D H. 2008. Viscoelastic BISQ model for low-permeability sandstone with clay.ChinesePhysicsLetters, 25(8):3079-3082.

Norris A N. 1985.A differential scheme for the effective moduli of composites.MechanicsofMaterials,4(1): 1-16.

O′Connell R J, Budiansky B. 1974.Seismic velocities in dry and saturated cracked solids.JournalofGeophysicalResearch,79: 5412-5426.

Pride S R, Berryman J G. 2003. Linear dynamics of double-porosity dual-permeability materials. I. Governing equations and acoustic attenuation.PhysicalReviewE, 68(3): 036603. Pride S R, Berryman J G, Harris J M. 2004.Seismic attenuation due to wave-induced flow.J.Geophys.Res., 109(B1): B01201.

Shapiro S A. 2003.Elastic piezosensitivity of porous and fractured rocks.Geophysics, 68(2): 482-486.

Tang X M. 2011. A unified theory for elastic wave propagation through porous media containing cracks—An extension of Biot′sporoelastic wave theory.Sci.ChinaEarthSci., 54(9): 1441-1452.

Yang D H, Zhang ZJ. 2002.Poroelastic wave equation including the Biot/squirt mechanism and the solid/fluid coupling anisotropy.WaveMotion, 35(3): 223-245.

Yang L, Yang D H, Nie J X. 2014.Wave dispersion and attenuation in viscoelastic isotropic media containing multiphase flow and its application.ScienceChina-PhysicsMechanics&Astronomy, 57(6): 1068-1077.Zimmerman R W. 1991. Compressibility of Sandstones. Amsterdam: Elsevier.Zimmerman R W. 1986.Compressibility of two-dimensional cavities of various shapes.JournalofAppliedMechanics, 53(3): 500-504.

附中文参考文献

陈颙, 黄庭芳. 2001. 岩石物理学. 北京: 北京大学出版社.

邓继新, 王尚旭, 杜伟. 2012. 介观尺度孔隙流体流动作用对纵波传播特征的影响研究—以周期性层状孔隙介质为例. 地球物理学报, 55(8): 2716-2727, doi: 10.6038/j.issn.0001-5733.2012.08.024.

(本文编辑 张正峰)

The influence of pore structure in reservoir sandstone on dispersion properties of elastic waves

DENG Ji-Xin1,2, ZHOU Hao2, WANG Huan2, ZHAO Jian-Guo3, WANG Shang-Xu3

1StateKeyLaboratoryofOilandGasReservoirGeologyandExploitation,ChengduUniversityofTechnology,Chengdu610059,China2DepartmentofGeophysicsandExploration,CollegeofGeophysics,ChengduUniversityofTechnology,Chengdu610059,China3CNPCKeyLaboratoryofGeophysicalProspecting,ChinaUniversityofPetroleum,Beijing102249,China

The pore structure of reservoir sandstone can significantly influence its elastic properties (e.g. elastic wave velocities), and also determine fluid-flow related wave dispersion and attenuation.In the common velocity dispersion models, only the compliant pore or crack with a fixed aspect ratio and concentration has been taken into account, while the fixed aspect ratio is considered as the “average”value of the rock, which is not completely realistic in reservoir rock. Because rock usually contains compliant pore (crack) showing a distribution of aspect ratios. This study presents a procedure to determine the pore aspect distribution of compliant pore (crack) from the pressure dependence of velocities. Based on the pore aspect distribution of compliant pore, a new method is suggested to extend the existing squirt flow model to consider the complex pore structure, especially when the aspect ratio has a relatively wide distribution.Based on micro-structure of a reservoir sandstone and the non-linear feature of velocities as a function of effective pressure, the pore system of the sandstone can be ideally classified into two groups, i.e. stiff pores with an aspect ratio larger than 0.01 and soft pores with an aspect ratio smaller than 0.01. In light of the poroelasticity theory, an analytic expression for the minimal initial aspect ratio is deduced under the assumption that the shape of soft pores is spheroidal. With this equation, a method to invert the distribution of the aspect ratio and corresponding pore volumes is presented by using the measured ultrasonic velocities as a function of pressure.Using an iterative procedure to add soft pore with different aspect ratios into the rock frame, the existing squirt fluid model of Gurevich is extended to consider complex pore structure of reservoir sandstones, especially when the aspect ratio has a relatively wide distribution.With the pore aspect ratio distribution, the extended Gurevich′s squirt-flow model is used to compute the wave velocities and attenuation as functions of frequency as well as pressure. When considering aspect ratio distribution of crack pore in the reservoir rock, the overall dispersion curve shows rapid velocity increase around a relatively wide squirt-flow relaxation frequency range of 1～104 Hz, which covers the typical seismic and sonic logging frequencies, indicating the mechanism of a continuous relaxation spectrum of the complex pore system. Compared with typical velocity dispersion curves based on a single aspect ratio squirt fluid model, the dispersion curves of the sandstone with a relatively wide distribution of aspect ratios do not show the low-frequency and middle-frequency range. This implies that for the rock samples at low pressure, it is not always profitable to employ Gassmann′s equation alone to predict the water-saturated velocities at typical seismic exploration frequencies. With the increasing pressure, velocity dispersion of the Gurevich′s squirt-flow model and the extended Gurevich′s squirt-flow model based on the aspect ratio distribution will decrease. To illustrate the validation of the extended Gurevich′s squirt-flow model, we compare predictions of our squirt model with laboratory measurement of two water-saturated sandstones at ultrasonic frequency of 700 kHz. We observe that the new model based on the pore structure is more accurate in predicting the pressure dependence of compression and shear velocities for the water-saturated sample than the Gassmann′s equation and Gurevich′s squirt-flow model. Our extended Gurevich′s squirt-flow model is consistent with Gassmann′s equation at low-frequency limit, and also with the Mavk-Jizba model at high-frequency.Through this study, we suggest that the squirt flow may be still important even in the seismic frequency band, and can cause apparent velocity deviation from the predictions based on Gassmann′s equation. Thus, our work can be considered as an important extension of the existing squirt fluid models.

Reservoir sandstone； Pore structure； Squirting fluid； Dispersion

邓继新, 周浩, 王欢等. 2015. 基于储层砂岩微观孔隙结构特征的弹性波频散响应分析.地球物理学报，58(9):3389-3400,

10.6038/cjg20150931.

Deng J X, Zhou H, Wang H, et al. 2015. The influence of pore structure in reservoir sandstone on dispersion properties of elastic waves.ChineseJ.Geophys. (in Chinese),58(9):3389-3400,doi:10.6038/cjg20150931.

10.6038/cjg20150931

P315

2014-04-22，2015-06-22收修定稿

国家自然科学基金项目(41374135)和国家重点基础研究发展计划(973)项目(2013CB228600)资助.

邓继新,1974年生,2003年毕业于北京大学获博士学位,2005年于中国石油大学博士后出站,从事地震岩石物理学和储层地球物理学研究. E-mail: dengjixin@cdut.cn