2011年MW9.0东日本大地震动力学破裂过程的数值模拟

刘敦宇, 胡才博, 蔡永恩

1 北京大学地球与空间科学学院地球物理系， 北京 100871 2 中国科学院计算地球动力学重点实验室， 北京 100049 3 中国科学院大学地球科学学院， 北京 100049



2011年MW9.0东日本大地震动力学破裂过程的数值模拟

刘敦宇1, 胡才博2,3, 蔡永恩1

1 北京大学地球与空间科学学院地球物理系， 北京 100871 2 中国科学院计算地球动力学重点实验室， 北京 100049 3 中国科学院大学地球科学学院， 北京 100049

力学上，地震可以看作在应力场作用下由于断层带介质的突然损伤或软化导致的断层带失稳事件.本文基于这个地震动力学模型，利用一种可以模拟断层大位错的有限元方法，研究了2011年MW9.0东日本大地震(Tohoku-Oki)的动力学破裂过程.比较了无障碍体和具有不同刚度障碍体的断层带模型产生的断层位移、位错和应力降.主要结果表明，障碍体的存在并不明显地改变障碍体区域的初始构造应力场.对有障碍体情形，准静态结果显示断层上盘最大逆冲位移和最大剪切位错分别为51 m和58 m，均发生在海底表面海沟处，与无障碍体的结果(最大剪切位错约55 m)相比差别不大；下盘最大倾向位移(-10 m)并不与上盘最大值出现在同一位置，而是在障碍体处.障碍体处剪应力降(约11 MPa)大于周围非障碍体区域.障碍体处正应力降的最大值约为3 MPa.模拟结果似乎不支持海山是导致本次地震异乎寻常大位错的原因，而倾向于断层带剪切刚度在地震过程中极度损伤或软化.

东日本大地震； 断层破裂过程； 断层位移； 应力降； 有限元方法

1 引言

发生于2011年3月11日的MW9.0东日本大地震(Tohoku-Oki)产生的巨大位错和海啸，大大出乎地震研究者的预料.海内外学者利用各种观测资料对其同震位错以及破裂过程进行了反演或联合反演(Lay et al.，2011；Yamazaki et al.，2011；Yue and Lay，2011；Simons et al.，2011；Ide et al.，2011；Yoshida et al.，2011；Zhang et al.，2012)，给出了本次地震准静态位错分布以及震源破裂过程等重要信息.然而如Lay等(2011)指出：利用地震波、GPS或者海啸等资料反演得到的同震位错差异较大，特别是分辨海沟附近断层面上位错量的大小和分布，这是由于数据对于近海沟的位错分辨能力有限.因此靠近海沟的观测数据就显得尤为重要.重复多激光束跨海沟测深数据表明本次地震在海沟附近产生了巨大的位移量：上盘介质朝向海沟水平位移量高达约50 m，垂直隆升约7到10 m(Fujiwara et al.，2011).准静态同震位错反演和震源破裂过程的运动学反演得到的最大位错从30 m到60 m不等.Lay等(2011)利用远震P波最小二乘反演得到断层东北部海沟附近最大位错达62 m.Yamazaki等人(2011)利用近场海啸数据约束反演的结果显示断层面上最大位错约60 m，集中在震源附近以及海沟附近.Simons等(2011)利用GPS和深海压力测量数据联合反演了本次地震的同震位错，其结果显示震源附近位错达到60 m.震源破裂过程的运动学反演中，Yue和Lay(2011)利用高频GPS资料反演破裂过程，结果显示位错较大的区域靠近海沟和震源，最大位错约60 m.Ide等(2011)利用宽频带地震波资料反演了本次地震的破裂过程，得到的最大累积位错值约30 m，靠近海沟.Yoshida等(2011)利用长周期(20～200 s)强地面震动数据反演破裂过程，结果显示本次地震分3个阶段，第一阶段破裂在断层北侧深部发展；第二阶段，浅部发生持续时间较长且位错量较大的破裂；第三阶段破裂在断层南段发展.最大位错位于断层北侧靠近海沟处，约47 m.Zhang等(2012)利用远震P波垂直分量和GPS数据联合反演了本次地震的破裂过程，其结果显示最大位错位于海沟处，为30 m.最大应力降达111 MPa，平均应力降46 MPa.

利用数值方法对地震断层破裂过程进行动力学正演能够提供震源行为的原因.Duan(2012)利用TSN (Traction-at-Split-Nodes)方法结合摩擦破裂准则正演了本次地震的自发破裂和地震波传播过程，结果表明位于震源上方的大小约70 km×23 km的海山对整个地震破裂过程起着重要的作用.海山处位错值最大，约47 m，且产生了超过50 MPa的剪切应力降.

JFAST(Japan Trench Fast Drilling Project)钻孔的结果能够提供关于断层带的材料和结构更多的认识(Chester et al.，2013).Chester等(2013)对本次地震的钻孔岩样进行了分析，结果表明：本次地震断层带厚度约5 m，材料区别于围岩介质，层内材料主要是粘土矿物,大位错主要发生在断层带薄层内.Wang和Kinoshita(2013)总结了JFAST得到的结果，认为该区域断层带厚度薄且强度弱是这次地震能够产生如此巨大位错的原因.

关于薄弱断层带对破裂过程影响的研究还比较少.为讨论弱断层带的影响，本文将用弹性三维节理单元(殷有泉和张宏，1982；殷有泉，2014)来模拟断层带薄层，并在胡才博等(2009)发展的模拟地震引起的稳态变形场的有限元方法基础上，继续研发了模拟断层破裂动力学过程的方法和程序，并用其模拟2011年东日本大地震的破裂过程和探讨它异乎寻常大位错的动力学机制.

2 有限元方法

野外地质考察和地震导波反演表明断层通常有一定的厚度(Li et al.，2002)，可以分为断层核、破损区和原岩三个主要区域(Caine et al.，1996；Gudmundsson，2004).从大地震前后的地震波速异常可以推断发震断层的力学性质在地震过程中发生了改变(Scholz，1990).因此地震可以看作在应力场作用下，由断层带介质的损伤或软化导致的断层带突然失稳事件.在这种地震动力学模型中，损伤或软化可以通过断层带介质的弹性参数降低(损伤力学本构)或其内摩擦系数和内聚力的减小(塑性力学本构)实现.地震断层的主要滑动集中在断层核(相对断层带的宽度而言非常窄)，因此如果不关心断层附近的变形场或应力场时，可以把断层视为没有厚度的位错面(地震运动学模型)或由摩擦强度控制的接触面(地震动力学模型或接触力学模型).无论是断层带模型还是位错或接触模型，虽然角度不同，它们都可以模拟地震断层滑动现象.本文将使用断层带介质弹性参数损伤的思想，研究2011年东日本大地震的断层破裂动力学过程，并探讨其大位错的动力学机制.

如果不考虑断层的动力学破裂过程，俯冲带断层地震引起的稳态变形场可以用有限元方法模拟(胡才博等，2009)

(1)

(2)

当断层带非常薄时，利用连续变形单元模拟断层带将会导致断层带内外单元刚度相差悬殊，使总体刚度矩阵条件数变差，较难模拟断层大位移滑动.为了有效地模拟断层大位移滑动，可采用能够模拟断层位移间断(位错)的节理元(殷有泉和张宏，1982；殷有泉，2014)，其相当于把断层两盘用弹簧连接起来.图1为节理元示意图，其沿倾向x′长L1，沿走向y′长L2，厚度为b.当L1≫b，L2≫b时，节理元内的应变可近似表达为

εx′≈0,εy′≈0,γx′y′≈0,εz′≈Δw/b,

γz′x′≈Δu/b,γz′y′≈Δv/b,

(3)

式中Δu,Δv,Δw分别为节理元沿断层倾向、走向和法向的位移间断量或位错.

利用断层坐标系x′，y′，z′定义的方向，断层上下盘的位移间断量可以表示为

Δu=[ΔuΔvΔw]T

=[u上-u下v上-v下w上-w下]T，

(4)

u上,v上,w上u下,v下,w下分别为节理元上下盘x′，y′，z′方向的位移，上角标“T”表示转置.本研究选用8节点六面体节理单元，每个节点有3个自由度，节点编号如图1所示，1,3,5,7号节点属于上盘，对应的下盘节点编号为2,4,6,8.

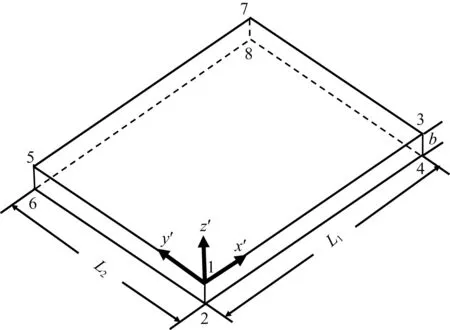
图1 节理元示意图(x′，y′，z′)为断层滑动坐标系. 节理元沿x′方向长L1，沿y′方向长L2，厚度b，其中L1≫b，L2≫b.1,3,5,7为上盘面节点编号，对应的下盘面节点编号为2,4,6,8.Fig.1 Schematic diagram of joint element in local fault coordinate system (x′, y′, z′)L1, L2 and b are its length, width and thickness, respectively. Nodal numbers of the element on the hanging wall fault surface are 1,3,5,7 and on footwall are 2,4,6,8.

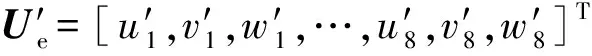
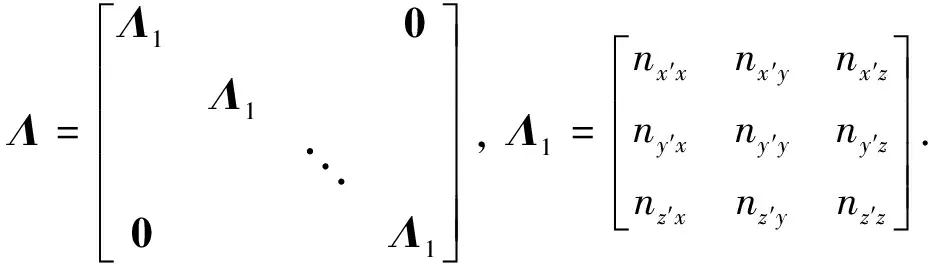
Δu=BUe,

(5)

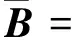
h5I-h5Ih7I-h7I],

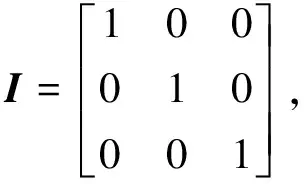
节理元的应力可以由位移间断量表示为

σ=DIIΔu,

(6)

σ=[τz′x′τz′y′σz′]T,

(7)

其中kz′x′,kz′y′,kz′z′分别为节理元倾向和走向(x′,y′)剪切面刚度以及法向(z′)面刚度，Gz′x′,Gz′y′,Ez′z′分别为节理元相应方向的剪切模量和杨氏模量.

由有限元方法(殷有泉，2014)，可以得到面积为s，厚度为b的节理元的单元刚度矩阵为

Ke=b∬sBTDBds.

(8)

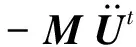
(9)

M,C分别为有限元模型的总体质量矩阵及总体阻尼矩阵，Kt为时刻t总体刚度矩阵，由于断层破裂区域随时间变化，所以Kt也是随时间变化.对于阻尼矩阵取为Rayleigh阻尼形式，即C=αM+βK，其中α主要控制低频成分的衰减，β主要控制高频成分的衰减.在实际岩石破裂过程中，大量的能量消耗在摩擦和破裂过程中，因此在利用弹性损伤模型时，需要在断层带介质上施加较大阻尼来模拟该能量损耗过程.

在获得构造运动加载引起的断层震前变形场U0或与其对应的背景应力场σ0后，利用公式(9)可以计算出在此应力场控制下，地震(断层损伤或软化)过程中的动态位移场Ut，利用(5)和(6)式可以求出断层上的位错和应力演化，由公式(10)可以得到地震应力降随时间的变化

Δσ(t)=σ(t)-σ0.

(10)

3 2011年MW 9.0东日本大地震的数值模拟

3.1 有限元模型及初始构造应力场

本文利用上述有限元方法模拟了2011年3月11日的MW9.0东日本大地震的破裂过程.构建的有限元模型如图2a所示.研究区域500 km×650 km×90 km，x轴方向为东偏北67°，y轴方向为东偏南23°，z轴方向为垂直地表向上.俯冲带(图2a中浅蓝色介质层)界面的几何模型参考日本海沟深度和历史地震剖面(Rhea et al.，2010)，设海沟深度7 km，在海底0～40 km深度，俯冲带倾角为11°；海底深度40 km以下俯冲带倾角为30°.断层带(图2a红框区域)设为夹在上盘介质和俯冲板片之间的5 m厚度的薄层(Chester et al.，2013).本次地震的断层破裂区如图2a黑框区域所示，其沿走向长250 km，沿倾向宽130 km.只有在破裂区内的断层带材料在地震过程中产生损伤或软化.

采用六面体网格剖分研究区域，并在靠近断层区域进行网格加密.断层带单元在断层面内的尺寸为1 km×1 km.模型上表面(地表和洋底)为自由表面；模拟初始构造应力场时，东南侧边界施加推挤位移边界条件，其他边界面施加滚筒约束.图2a中，红星处为震源，深度26 km.测线AB位于模型上表面且垂直于断层迹线(海沟)；测线CD位于断层面(地表和洋底)且垂直于断层迹线.

有学者把本次大地震异常大的滑动归因于海山障碍体的破裂(Yoshida et al.，2011；Duan，2012).从断层带介质的弹性参数的角度看，障碍体(可能为海山)可视为刚度较大岩石材料，为讨论其对断层位移、位错以及应力降的影响，我们设计了不存在障碍体(模型A)和两个存在障碍体(模型B和C)的三种断层模型.对于模型B和C，在断层带破裂区设置了一个尺度为70 km×31 km的障碍体(如图2c断层破裂区中间的浅蓝色区域)，走向方向从290～360 km，倾向从-26.2～-57.6 km.

这三个模型的断层带外部的材料参数均相同(PREM模型)，如表1所示.鉴于JFAST钻孔得到的浅部(海底下812 m)断层带主要由粘土类矿物组成(Chester et al.，2013)，我们参考Mondol等(2007)对于粘土聚合物压缩试验的研究结果设置断层带的材料参数.为区别断层带的破裂和未破裂区，本文假设未破裂断层带的材料参数高于破裂区.根据Mondol等人的研究结果，如果考虑孔隙流体影响，断层带内的弹性常数大小与有效应力有关：对于模型A，选取破裂区的材料为垂直有效应力10 MPa时的杨氏模量2.0 GPa和剪切模量0.7 GPa；未破裂区的杨氏模量和剪切模量分别为20 GPa和7 GPa.参考Duan(2012)利用比非障碍体断层区域较高的静摩擦系数、较低的孔隙压力以及较高的初始应力来模拟障碍体.本研究的模型B中，假设障碍体仍为粘土聚合物，但其材料参数选择垂直有效应力较高时(50 MPa)的剪切模量和杨氏模量，分别为1.75 GPa和5 GPa，其剪切模量为破裂区非障碍体的2.5倍；在模型C中，假设障碍体为海山，物质来源为海洋地幔，其杨氏模量和剪切模量分别取为151 GPa和59.3 GPa(参见表1)，其中剪切模量为破裂区非障碍体的84倍.除了障碍体材料参数的差别，模型B和C的区别还在于模型B的障碍体在地震中剪切面刚度损伤更严重.

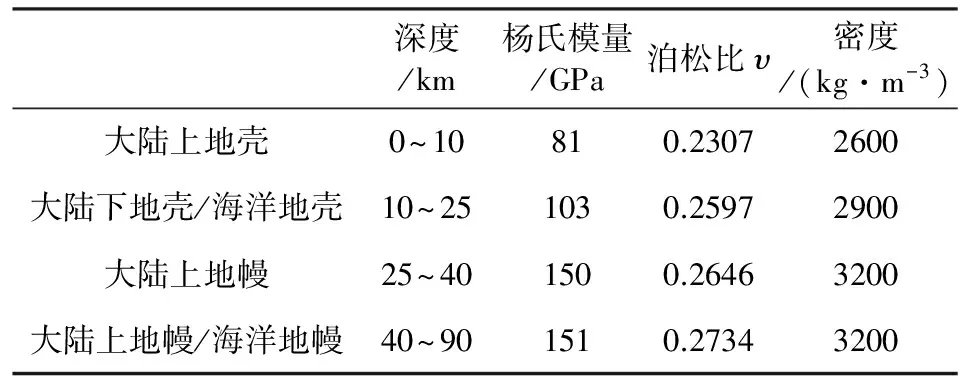
表1 有限元模型材料参数Table 1 Material parameters in the finite element model

本文将主要讨论模型B的结果.为方便起见，如无特殊说明，后文中的断层或断层带专指断层带破裂区.

为了模拟地震断层的破裂过程，需要模拟震前的构造应力场.假设地震遵循弹性回跳学说，并且本次大地震把构造运动积累起的弹性能全部释放(Ide et al.，2011)，那么断层带上初始构造剪应力应该与剪应力降大小相近.根据Simons等(2011)估算的本次地震应力降约为2到10 MPa，当在本模型东南侧边界施加累积推挤位移240 m时(如图2a所示)，断层带初始构造剪应力在10 MPa左右.假设太平洋板块一直以80～85 mm·a-1(Simons et al.，2011)的速率向日本岛俯冲，要在断层带积累起这么大的初始剪应力需要约2900年.因为海水基本不可压缩，在海底表面，地震引起的海水载荷变化与地震断层应力降相比可以忽略，因此，地震动力载荷在此处可视为零(表面自由).

图2c和2d分别为由边界推挤240 m得到的断层上盘面初始剪应力和正应力(正应力和剪应力的正方向如图2b所示).由图2c可见，在构造运动加载下，断层破裂区上积累起的剪应力随深度增加而增大.其中海底海沟处(水深度7 km)剪应力最小，约为9 MPa；最大值位于断层深部，约为15 MPa.障碍体上的初始剪应力略大于周围断层带，特别是在障碍体边界上，剪应力(13.1 MPa)高于周围非障碍体断层带0.5 MPa，这是由于该处材料不连续所致.从图2d上可看到，断层面法向呈挤压状态，在障碍体处正应力较周围大，最大值约3.3 MPa.倾向位于-20～-60 km的非障碍体区域的正应力较大.此外，从图中可以看到材料分界引起的应力集中.

两种障碍体模型(B和C)的初始剪应力仅在障碍体边界处与模型A区别较大.在障碍体边界处，模型C的初始剪应力比模型A约大1 MPa，障碍体内部初始应力状态与模型A相差不多，这是由于在本研究所采用的构造应力场的加载方式下，障碍体虽然刚度较大，但其应变较小.

3.2 模拟结果及分析

地震过程通过逐步下降断层带的剪切刚度模拟.刚度下降多少可以利用观测资料或反演得到的断层位错量来约束.Yoshida等(2011)指出破裂传播速度在此次地震过程中约3～4 km·s-1.本文假设断层破裂以圆盘形式传播且破裂传播速率为3 km·s-1.模拟所选时间步长为0.5 s，以保证在每一个时间步长内均有断层带单元破裂.在初始构造应力场作用下，当破裂传至某一断层带单元时，即降低其倾向剪切面刚度，降低后不再恢复.通过给断层带上下盘质点施加大阻尼来模拟地震过程中的能量耗散.

数值试验表明：对于模型B，若产生约58 m的最大剪切位错(Lay et al.，2011；Yue and Lay，2011)，地震断层带非障碍体单元的倾向剪切面刚度需损伤至0.1 MPa/m(剪切模量损伤至0.5 MPa)，障碍体倾向剪切面刚度需损伤至0.02 MPa/m(剪切模量损伤至0.1 MPa).在模型A和C中，所有地震断层带单元倾向剪切面刚度均损伤至0.1 MPa/m.非断层带介质阻尼系数α=0.1，β=0.03.由于断层带单元很薄，所以需施加较大阻尼模拟破裂和摩擦过程中的耗散，数值试验给出断层带单元阻尼系数α=1000.0，β=0.03.

图3a给出了破裂开始后六个不同时刻的倾向剪切位错快照(正值表示上盘介质相对下盘沿倾向向上运动).在33 s时，破裂刚刚到达海沟；在150 s左右，破裂趋于稳定，这个结果与运动学反演结果一致(Zhang et al.，2012).对比34～70 s的快照图，可以看到海沟处的位错在36 s内从不到10 m增大到40多米；在随后70～150 s内，海沟处位错逐渐增加到58 m.从70～150 s的快照图中可以看到，最大值剪切位错为58 m，位于海沟处；障碍体处及位于障碍体前方的断层带浅部的位错值均比较大.如此大的位错量可能是因为震后断层带很弱(倾向剪切面刚度只有0.1 MPa/m)和断层倾角很低，当破裂破穿海沟后，下盘介质无法有效地约束上盘介质.

图3b给出了破裂开始后六个不同时刻的法向位错快照(正值表示拉张).动态最大幅值约0.07 m，与断层倾向位错相比非常小.法向位错稳定后的幅值不超过0.02 m.断层上半部分震后法向位错为拉张，而下半部分为压缩.障碍体处由于法向刚度较大，所以位错较小，但仍为拉张状态.

根据位错分布以及断层围岩剪切模量可以计算地震矩，其计算公式(Aki，1966)为

M0=μAD,

其中μ为断层围岩剪切模量，D为断层平均位错，A为断层面积.对于位错分布不均匀且断层围岩材料不均匀的情况，可计算地震矩密度m0=μD，并对整个断层面积分得到总地震矩.在本研究中，在一些断层区域上下盘围岩的剪切模量有可能不同，此时取其平均值.图4给出了地震矩密度分布.对断层面积分得到本次地震的地震矩M0=3.98×1022N·m.由矩震级计算公式(Kanamori, 1977)

得到矩震级MW=9.0.该结果与USGS给出的矩震级一致.

地震在150s时已经基本停止，图5a—5d展示了震后200s时断层带的位移(位移正方向如图2b所示)和位错分布.图5a为断层上盘面逆冲位移分布图，最大值51m，位于海沟处.图5b为断层下盘面倾向位移分布图，最大值-10m，位于障碍体处；断层边界处位移值为正，说明该处介质被上盘拖曳向海沟方向运动.图5c和5d分别为断层上盘面和下盘面法向位移分布，最大值2.6m，位于断层底边界；断层浅部沿断层下盘面外法线方向平均位移了约2m，断层深部沿断层上盘面外法线方向平均位移了约2m.

图2 (a)有限元模型; (b)断层上下盘面应力和位移的正方向示意图; (c)断层上盘面初始倾向剪应力; (d)断层上盘面初始法向正应力Fig.2 (a) Finite element model; (b) Definition of the positive directions of displacements and stresses on the fault surfaces; (c) Initial shear stress on the hanging wall fault surface; (d) Initial normal stress on the hanging wall fault surface

图3 断层位错快照(a)倾向剪切位错; (b)法向位错.Fig.3 Snapshots of dislocation(a) Shear dislocation; (b) Normal dislocation.

图5 震后200 s断层面上的位移和位错分布(a)和(b)分别是断层上盘和下盘剪切位移；(c)和(d)分别是断层上盘和下盘法向位移；(e)、(f)和(g)分别是断层上盘、下盘AB测线上的6个测点的剪切位移和剪切位错随时间变化.Fig.5 Displacement and dislocation distributions on the fault surfaces at 200 s(a) and (b) are shear displacements of the hanging wall and footwall, respectively; (c) and (d), normal displacements of the hanging wall and footwall, respectively; (e), (f) and (g), shear displacements of the hanging wall, footwall and shear dislocation at six observation sites on Profile AB, respectively.

图6 CD测线在不同时刻的位移(a) 水平位移; (b) 垂向位移. 横坐标‘0’和负值分别表示断层在海沟的出露点和断层上盘.Fig.6 Displacements on the profile CD at different times(a) Horizontal displacements; (b) Vertical displacements. ‘0’ and negative coordinate value represent the trench and the hanging wall, respectively.

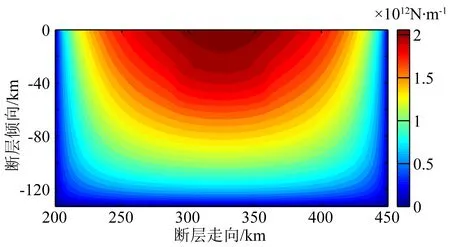
图4 地震矩密度分布Fig.4 Seismic moment density distribution

图5e—5g展示了图2a中位于断层上的AB测线上6个测点的位移和位错随时间变化(位移正方向如图2b所示).0号测点为震源，深度26km；1号测点深度22km；3、2号测点分别为障碍体的上下边界所在深度，分别为12km和18km；4号测点深度8.9km；5号测点位于海沟处，深度7km.图5e为断层上盘面逆冲位移，海沟处位移值最大，为51m.图5f为断层下盘面倾向剪切位移，6个测点中3号(深度为-12km)测点处位移值最大，略小于-10m.图5g为断层倾向剪切位错，海沟处测点位错最大，为58m.比较六条曲线的斜率可以看出，断层初始滑动速率(断层上一点在单位时间内位错的大小)随着破裂向海沟传播逐渐增大：破裂初始阶段为0.7m·s-1(震源，0号测点)，逐渐增大到2m·s-1(3号测点)，当破裂达到海沟时，高达6m·s-1(5号测点)，这是由于破裂前端动力积累的应力集中导致的雪崩式的结果.

图6为位于地表和洋底的CD测线(图2a)在不同时刻水平方向和垂向位移.从图中可以看到非常明显的弹性回跳的动态过程：随着破裂向海沟扩展，上盘地表最大水平位移和垂直位移的位置向海沟移动；在33s时，破裂即将传至海沟，该处介质变形达到最大；在34s时海沟破裂，上下盘介质即刻产生显著相对位移并随时间迅速增大.从图6a可以看到，地震引起的主要地表变形来自上盘：在海沟处，上盘在150s时垂直于海沟向下盘水平位移了近50m，而下盘的位移量仅约8m.从图6b可以看到：在海沟处，上盘在150s时垂直隆升达12m，足以产生巨大的海啸.本文的结果与重复多激光束跨海沟测深(Fujiwaraetal.，2011)得到的结果比较一致.

图7a和7b展示了震后200s时断层上盘面剪应力降和正应力变化分布(应力变化的正方向如图2b所示).应力变化按照公式(10)计算，正值表示应力降，负值表示应力增加.剪应力降随着深度的增大而增大，这主要是因为断层面上初始剪应力随深度增加而增大且本文假设断层带材料损伤量相同.障碍体处应力降(约11MPa)比周围非障碍体处(约9MPa)大.由于断层带法向刚度没有损伤，法向应力变化趋势同法向位错：以倾向深度-80km线为分界，倾向位于0～-80km的断层带区域法向正应力释放；-80～-130km的区域法向正应力增加.障碍体区域法向正应力释放较大，约2～3MPa.

图7c和7d分别为AB测线上6个测点处的剪应力和正应力变化随时间变化图.从图7c可以看到，动态应力降大于准静态应力降.当破裂传播到新的破裂部位之前，由于断层破裂的端部效应，该处会产生较大的应力增加(负值).断层破裂过程中，正是由于这种迅速增加的端部动态应力，使断层破裂得以持续，直到碰到高强度的障碍体或者初始应力很低的断层带介质使破裂停止.图7d表明，动态正应力变化的幅值振动幅度达10MPa；地震结束后，倾向位于0～-80km区域的测点法向应力增加约1MPa，而位于-80～-130km区域的测点法向应力降约2MPa.

图8a—8d分别给出了无障碍体情况下(模型A)的剪切位错、法向位错、断层上盘面剪切应力降以及法向应力降(负值表示应力增加).

图8e—8h分别为有障碍体情况(模型B)与模型A的剪切位错、法向位错、断层上盘面剪切应力降以及法向应力降(负值表示应力增加)的差值分布(用模型B减去模型A).结果显示：障碍体处(模型B)的剪切位错要比A模型大3～5m，并且障碍体前方(向海沟方向)位错也相应增大.由于障碍体处初始剪应力没有明显高于无障碍体情况，上述3～5m的差位错是由障碍体更多的材料损伤，破裂后上下盘更容易滑动导致.相应的障碍体处的剪应力降要比没有障碍体的情形约大3～5MPa；相应的法向应力降在障碍体上半部分及其前方(向海沟方向)比模型A约大1MPa.

图8i—8l分别为有障碍体情况(模型C)与模型A的剪切位错、法向位错、断层上盘面剪切应力降以及法向应力降的差值分布(用模型C减去模型A).结果显示：当障碍体和非障碍体断层带倾向剪切面刚度均损伤至0.1MPa/m时，障碍体处(模型C)的剪切位错并没有明显大于模型A，最大位错差只有0.1m.模型C的剪应力降仅在障碍体边界处比模型A约大2MPa.

综上所述，当断层带材料均损伤至同一值时，即便障碍体的材料参数为非障碍体材料参数84倍(模型C)，其震后断层位错分布并没有明显区别于无障碍体模型(模型A).如果障碍体处断层带材料损伤后，剩余剪切刚度更低的话(模型B)，障碍体处及障碍体前方的位错仅比无障碍体模型大3～5m.因此障碍体可能不是导致东日本大地震异乎寻常大滑动的主要原因，即使没有障碍体，当断层带剪切面刚度损伤至0.1MPa/m时，仍会产生高达55m的最大剪切位错.

4 结论与讨论

本文利用能够模拟断层大位移间断的三维弹性节理单元探讨了2011年东日本大地震的断层破裂动力学过程.对于有、无障碍体模型，主要认识如下：

这次大地震的断层初始剪应力随深度增加而增大.对于障碍体的剪切模量和非障碍体断层带的差别不大时(模型B)，障碍体边缘处初始剪应力约为13.1MPa，略高于同一深度无障碍体断层带区域；障碍体法向初始挤压应力最大值约3.3MPa.对于障碍体的剪切模量大大高于非障碍体断层带时(模型C)，障碍体边缘初始剪应力只比模型B约大0.5MPa.即不同刚度的障碍体不会显著改变断层面上的初始应力状态.

对于模型B，地震引起的倾向剪切位错和断层上盘面逆冲位移最大值在海沟处，分别为58m和51m.地震引起的断层下盘面倾向位移最大值不在海沟，而位于障碍体区域，为-10m.地震引起的洋底变形主要由上盘产生.在海沟处，上盘介质向海沟方向水平位移了近50m，垂向隆升近12m，模拟结果与重复多激光束跨海沟测深数据结果一致.断层带破裂后，其残余刚度很小，下盘介质无法有效地约束上盘介质，而且本次地震断层倾角很低，这可能是本次地震能够产生如此巨大位错的主要原因.障碍体的影响有限.

对于模型B，障碍体处剪应力降大于其周围非障碍体断层带区域.如果考虑了断层厚度，震后法向正应力在断层深部增加，而浅部减小.

如果假设太平洋板块平均以80～85mm·a-1速率向日本岛俯冲以及本次地震的断层破裂区构造剪应力全部释放，构建初始构造应力场的结果表明这个地区MW9.0大地震的复发期约2900年.

利用简单的断层带弹性材料损伤或软化模型模拟地震过程还存在着一定的局限性，例如在破裂前端，存在很大的应力集中.真实岩石材料在应力达到其屈服强度后，将会产生塑性变形，因此利用弹塑性介质模拟断层带可能更加符合实际，并能通过破裂准则判断和预测破裂的发展，这也将是下一步工作需要考虑的方向.

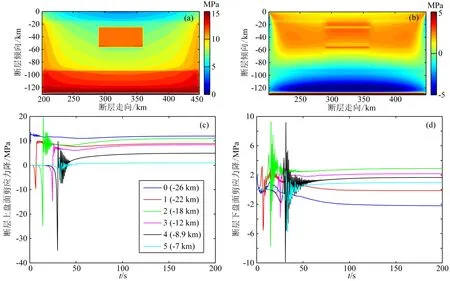
图7 震后200 s断层上盘面应力变化(a) 剪切应力降；(b) 正应力变化; (c)和(d)分别是AB测线上6个测点剪切应力降和正应力变化随时间变化曲线.Fig.7 Stress changes on the hanging wall fault surface at 200 s(a) and (b) are distributions of shear stress drop and normal stress change, respectively; (c) and (d), shear stress drop and normal stress change at six observation sites on Profile AB, respectively.

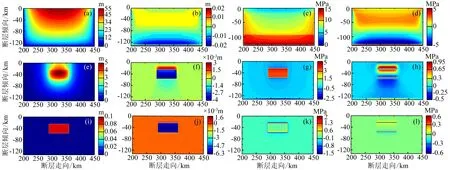
图8 有、无障碍体模型的断层位错和应力降比较(a)—(d)分别是A模型 (无障碍体)的剪切位错、法向位错、断层面剪应力降和断层面法向正应力降；(e)—(h)分别是模型B与模型A的剪切位错之差、法向位错之差、断层面剪应力降之差和断层面法向应力降之差；(i)—(l)分别是模型C与模型A的剪切位错之差、法向位错之差、断层面剪应力降之差和断层面法向应力降之差Fig.8 Comparisons of the fault dislocation and stress drop among the models with and without the asperityModel A (without asperity): (a) shear dislocation; (b) normal dislocation; (c) shear stress drop; (d) normal stress drop. Comparisons of differences of the shear dislocation (e), the normal dislocation (f), the shear stress drop (g), and the normal stress drop (h) between Model B and Model A; Comparisons of differences of the shear dislocation (i), the normal dislocation (j), the shear stress drop (k), and the normal stress drop (l) between Model C and Model A.

Aki K. 1966. Generation and propagation of G waves from the Niigata earthquake of June 14, 1964. Part 2. Estimation of earthquake moment, released energy, and stress-strain drop from G-waves spectrum.BulletinoftheEarthquakeResearchInstitute, 44: 73-88.

Caine J S, Evans J P, Forster C B. 1996. Fault zone architecture and permeability structure.Geology, 24(11): 1025-1028.

Chester F M, Rowe C, Ujiie K, et al. 2013. Structure and composition of the plate-boundary slip zone for the 2011 Tohoku-Oki earthquake.Science, 342(6163): 1208-1211, doi: 10.1126/science.1243719.

Duan B C. 2012. Dynamic rupture of the 2011MW9.0 Tohoku-Oki earthquake: Roles of a possible subducting seamount.J.Geophys.Res., 117: B05311, doi: 10.1029/2011JB009124.

Fujiwara T, Kodaira S, No T, et al. 2011. The 2011 Tohoku-Oki earthquake: displacement reaching the trench axis.Science, 334(6060): 1240, doi: 10.1126/science.1211554.

Gudmundsson A. 2004. Effects of Young′s modulus on fault displacement.ComptesRendusGeoscience, 336(1): 85-92.

Hu C B, Zhou Y J, Cai Y E. 2009. A new finite element model in studying earthquake triggering and continuous evolution of stress field.Sci.ChinaSer.D-EarthSci., 52(7): 994-1004, doi: 10.1007/S11430-009-0082-3.

Ide S, Baltay A, Beroza G C. 2011. Shallow dynamic overshoot and energetic deep rupture in the 2011MW9.0 Tohoku-Oki earthquake.Science, 332(6036): 1426-1429, doi: 10.1126/science.1207020.

Kanamori H. 1977. The energy release in great earthquakes.J.Geophys.Res., 82(20): 2981-2876.

Lay T, Ammon C J, Kanamori H, et al. 2011. Possible large near-trench slip during the 2011Mw9.0 off the Pacific coast of Tohoku earthquake.Earth,PlanetsandSpace, 63(7): 687-692.Li Y G, Vidale J E, Day S M, et al. 2002. Study of the 1999M7.1 Hector Mine, California, earthquake fault plane by trapped waves.Bull.Seismol.Soc.Am., 92(4): 1318-1332.

Mondol N H, Bjørlykke K, Jahren J, et al. 2007. Experimental mechanical compaction of clay mineral aggregates-Changes in physical properties of mudstones during burial.MarineandPetroleumGeology, 24(5): 289-311.

Rhea S, Tarr A C, Hayes G P, et al. 2010. Seismicity of the Earth 1900-2007, Japan and vicinity. U. S. Geological Survey, Open-File Report 2010-1083-D.

Scholz C H. 1990. The Mechanics of Earthquakes and Faulting. New York: Cambridge University Press.

Simons M, Minson S E, Sladen A, et al. 2011. The 2011 magnitude 9.0 Tohoku-Oki earthquake: Mosaicking the megathrust from seconds to centuries.Science, 332(6036): 1421-1425, doi: 10.1126/science.1206731.

Wang K L, Kinoshita M. 2013. Dangers of being thin and weak.Science, 342(6163): 1178-1180, doi: 10.1126/science.1246518. Yamazaki Y, Lay T, Cheung K F, et al. 2011. Modeling near-field tsunami observations to improve finite-fault slip models for the 11 March 2011 Tohoku earthquake.Geophys.Res.Lett., 38(7): L00G15, doi: 10.1029/2011GL049130.

Yin Y Q. 2014. Plastic Mechanics of Rock-Like Materials (in Chinese). Beijing: Peking University Press.

Yin Y Q, Zhang H. 1982. A mathematical model of strain softening in simulating earthquake.ChineseJ.Geophys.(ActaGeophysicaSinica) (in Chinese), 25(5): 414-423. Yoshida K, Miyakoshi K, Irikura K. 2011. Source process of the 2011 off the Pacific coast of Tohoku Earthquake inferred from waveform inversion with long-period strong-motion records.Earth,PlanetsandSpace, 63(7): 577-582.

Yue H, Lay T. 2011. Inversion of high-rate (1 sps) GPS data for rupture process of the 11 March 2011 Tohoku earthquake (MW9.1).Geophys.Res.Lett., 38(7): L00G09, doi: 10.1029/2011GL048700. Zhang Y, Xu L S, Chen Y T. 2012. Rupture process of the 2011 Tohoku earthquake from the joint inversion of teleseismic and GPS data.Earthq.Sci., 25(2): 129-135, doi: 10.1007/s11589-012-0839-1.

附中文参考文献

胡才博, 周一杰, 蔡永恩. 2009. 如何用有限元新模型研究地震触发和应力场连续演化. 中国科学D辑: 地球科学, 39(5): 546-555.殷有泉. 2014. 岩石类材料塑性力学. 北京: 北京大学出版社.

殷有泉, 张宏. 1982. 模拟地震的应变软化的数学模型. 地球物理学报, 25(5): 414-423.

(本文编辑 何燕)

Numerical simulation of the dynamic rupture process of the 2011 Tohoku-Oki, JapanMW9.0 earthquake

LIU Dun-Yu1, HU Cai-Bo2,3, CAI Yong-En1

1InstituteofTheoreticalandAppliedGeophysics,PekingUniversity,Beijing100871,China2KeyLaboratoryofComputationalGeodynamics,ChineseAcademyofSciences,Beijing100049,China3CollegeofEarthScience,UniversityofChineseAcademyofSciences,Beijing100049,China

Earthquakes can be considered as an unstable dynamic process of stress release induced by sudden softening or damage of material on faults. Based on this idea, a finite element method is proposed to simulate the dynamic rupture process of the 2011 Tohoku-Oki, JapanMW9.0 earthquake to find a mechanical explanation for the extremely huge fault slip.According to the results from JFAST (Japan Trench Fast Drilling Project), the ruptured area of this earthquake is modeled as a 5 m-thick layer, which is 250 km along strike and 130 km along dip direction. An asperity of 70 km by 31 km with different material properties is placed at the middle of the ruptured area. A 3-D linear elastic joint element is used to model the fault zone and corresponding equations of the finite element method are derived. The method consists of two parts: (1) The tectonic initial stress field is induced by boundary displacement. (2) Under the initial stress, the rupture process is modeled by gradually reducing the shear modulus of the ruptured area (rupture propagates as expanding circles with a rupture velocity of 3 km·s-1). The amount of reduction of shear modulus in the fault zone is constrained by matching maximum slip from the geodesy observation or inversion results of previous studies.The simulated tectonic stress field shows that shear stress increases with depth. Its minimum value is about 9 MPa at the trench and maximum value is about 15 MPa at depth. The existence of an asperity does not change the initial tectonic stress in the ruptured area remarkably. The displacements, slips and stresses predicted by the models with and without asperities are discussed. If an asperity exists, to match the fault displacements observed at the sea floor, the shear modulus of the asperity and that of non-asperity area have to be reduced to 0.5 MPa and 0.1 MPa, respectively. The maximum quasi-static shear displacement on the hanging wall is 51 m at the trench surface, and that on the footwall is 10 m at the asperity. The maximum fault slips with and without the asperity are 58 m and 55 m, respectively. Both of them appear at the trench surface and their difference is not obvious. At the trench, the hanging wall moves about 50 m horizontally towards the trench and uplifts 12 m, which is consistent with the result of repeated multibeam bathymetric surveys. Shear stress drop at the asperity (about 11 MPa) is larger than that in its surrounding area. Maximum normal stress drop (about 3 MPa) appears at the asperity.Based on the initial tectonic stress simulation, given that the Pacific plate moves towards Japan islands at a rate of 80～85 mm·a-1and that tectonic shear stress is totally released during this earthquake, the recurrence time ofMW9.0 in this area is estimated to be about 2900 years. The predicted results of this paper do not support the inference that the rupture of an asperity is responsible for the unusually large slip of the Tohoku-OkiMW9.0 earthquake, instead the huge damage of fault zone material might be the reason.

Tohoku-Oki earthquake; Fault rupture process; Displacements on fault; Stress drop; Finite element method

刘敦宇, 胡才博, 蔡永恩. 2015. 2011年MW9.0东日本大地震动力学破裂过程的数值模拟.地球物理学报，58(9):3133-3143,

10.6038/cjg20150910.

Liu D Y, Hu C B, Cai Y E. 2015. Numerical simulation of the dynamic rupture process of the 2011 Tohoku-Oki, JapanMW9.0 earthquake.ChineseJ.Geophys. (in Chinese),58(9):3133-3143,doi:10.6038/cjg20150910.

10.6038/cjg20150910

P315

2014-05-30，2015-04-16收修定稿

国家自然科学基金(41474080)资助.

刘敦宇，男，1988年生，主要从事震源破裂过程数值模拟研究.E-mail：dunyuliu@gmail.com