基于CHAMP卫星与三维Taylor多项式模型的区域地磁建模研究

蒋勇， 姜乙， 冯彦*，刘宝嘉， 傅帅，常德， 张鹏飞， 江涛

1 南京信息工程大学空间天气研究所， 南京 210044 2 中国科学院空间天气学国家重点实验室, 北京 100190



基于CHAMP卫星与三维Taylor多项式模型的区域地磁建模研究

蒋勇1，2， 姜乙1， 冯彦1，2*，刘宝嘉1， 傅帅1，常德1， 张鹏飞1， 江涛1

1 南京信息工程大学空间天气研究所， 南京 210044 2 中国科学院空间天气学国家重点实验室, 北京 100190

利用CHAMP卫星矢量和标量地磁测量数据，通过三维Taylor多项式模型建立了2010.0年中国及邻近地区在300 km高度附近的X、Y、Z和F分量的三维磁场模型.为了比较验证所建模型，分析了其与Taylor多项式模型(二维模型)不同截断阶数所对应的均方偏差(RMSE)、残差及分布等.结果表明，三维模型每一阶的RMSE和残差绝对值的平均值均要比二维模型的小约45%.由于采用了系数完全展开的建模方式，三维模型的系数数量约为二维模型的2倍，三维模型较低的截断阶数可以反映更多的地磁信息.本研究中的5阶三维Taylor模型基本可达到8阶Taylor模型的精度.两种模型绘制的地磁场及残差分布有较好的一致性.

地磁模型； 三维Taylor多项式模型； CHAMP卫星； 均方偏差

1 引言

区域地磁场模型用以反映某个区域的地磁场的时空分布特征.相比于全球地磁场模型(Hurwitzd et al.，1966；IAGA，2003，2005，2010；冯彦等，2014a)，结合高密度的地面实测数据，区域模型能更精确地反映区域内的地磁场分布，如地磁场在特定区域内所呈现的一些变化规律和异常分布.

常用的区域地磁场模型包括Taylor多项式模型、曲面Spline模型(安振昌和徐元芳，1981；安振昌等，1982)、矩谐模型(Alldredge，1981)、Legendre模型、自然正交分量(NOC)模型、球冠谐模型(Haines，1985)等.国内外学者已利用这些区域模型做了很多研究.如，Alldredge(1982)利用矩谐模型研究美国东南部区域磁场.Haines(1985)利用球冠谐模型分析了加拿大区域1960—1983年的磁场变化.Düzgit等(1997)利用矩谐分析研究了欧洲区域的地磁场.Thébault等(2004，2006)(Thébault and Gaya-Piqué，2008)将原有的球冠谐模型进行了改进，并利用改进后的模型研究了法国地区的地磁场(Thébault，2008).国内学者主要针对中国地区开展了一些研究.徐文耀和朱岗昆(1984)利用矩谐分析研究了我国及邻近地区的地磁场.高金田等(2006)运用曲面Spline模型研究了1900-1936年中国区域地磁场以及其长期变化的分布.陈斌等(2011)运用球冠谐模型计算2005年中国地区地磁场及其长期变化.

相比于其他的区域模型，Taylor多项式模型由于其计算简单及使用方便，得到了广泛的应用.如安振昌等(1991a)利用Taylor多项式模型建立了1950—1980年中国地区主磁场模型.徐元芳等(1992)运用Taylor多项式模型计算了1950—1985年中国地区地磁场长期变化模型.高金田等(2005)利用2003年中国地区的地磁台站数据建立Taylor多项式模型对中国地区的地磁场进行了研究.冯彦等(2010c)利用2000年中国地磁台站和复测点数据，根据Taylor多项式模型计算了2000年中国地区地磁场.

尽管存在上述优点，但Taylor模型是二维模型，建模时只考虑了经度与纬度，而忽略了高度因素.地磁场的强度随着高度变化而变化，一般以20 nT/km的速率减少(安振昌等，1991b)，因此二维模型所计算的地磁场强度会存一定的误差.针对此问题，柳士俊等(2011)提出了三维Taylor多项式模型，考虑了高度的因素，为区域模型的研究提供了一种新的方法.

在以往的研究中，建立和计算区域地磁场模型所采用的数据大多来自于地磁复测点、台站数据或者利用其他模型所模拟的数据.由于地磁复测点和台站数量有限，且空间分布很不均匀，这将直接影响所建模型的精度.另外由于缺少国界外测点，使得在边界区域上的模拟会出现异常，即边界效应.一般解决边界效应的方法有添加边界外区域的补充点和扩大拟合区范围两种(杨云涛等，2009).补充点的数据通常来自于其他模型，如国际地磁参考场(IGRF).这种数据本身就存在一定的误差，因此会进一步影响所建立模型的精度.扩大拟合区范围后，虽然在拟合区中心的高精度范围扩大，但拟合区的边界异常仍没得到解决.

对于CHAMP卫星的磁测数据，国内外学者做了大量的研究工作.如Sabaka等(2004)利用CHAMP等卫星数据建立了第四代地磁场模型综合模型——CM4.Olsen等(2006)利用CHAMP等卫星数据建立了CHAOS模型系列.Maus等(2007)利用CHAMP卫星数据建立了岩石圈磁场模型(MF)系列.康国发等(2009，2010)基于CHAMP卫星数据建立的POMME-4.2S模型研究了中国及邻近地区的长期变化、长期加速度以及磁异常的分布特征.然而，将CHAMP卫星磁测数据进行中国大陆地区的地磁场研究至今还鲜有报道.

针对目前研究现状，认为基于CHAMP卫星所提供的高精度、高密度的全球地磁标量数据和矢量观测数据进行中国及邻近地区的地磁场三维建模对于研究中国，乃至东亚地区的高精度地磁场形态分布具有重要的理论和应用价值.现拟首先对CHAMP卫星数据进行数据预处理及网格化，得到中国地区卫星地磁网格数据，然后基于不同位置和高度的卫星数据建立中国及邻近地区的三维Taylor多项式模型(三维模型)，分析了4个地磁要素(X、Y、Z、F)的分布特点，研究了截断阶数对模型精度的影响，并在拟合值、残差分布，截断阶数与RMSE值等方面与常用的Taylor多项式模型(二维模型)进行比较分析.

2 数据与方法

2.1 数据

地磁场为一向量场，地球空间任意一点都包含7个地磁场要素，分别为地磁场总强度F，北向分量X，东向分量Y，垂直分量Z，水平强度H，磁偏角D和磁倾角I.CHAMP卫星提供了2001—2010年的地磁标量数据(F)和矢量数据(X、Y、Z)，所有数据由德国地球科学研究中心(GFZ)网站(http:∥www.gfz-potsdam.de/startseite/)提供.CHAMP卫星于2000年7月15日从俄罗斯的Plesetst卫星发射基地发射至近极轨、环形、高约454 km的轨道.卫星搭载的Overhauser磁力计(OVM)测量标量数据，磁通门磁力计(FGM)测量矢量数据(冯彦等，2010a).

由于所测量的矢量数据是在FGM参考坐标系下获取的，因此还需要将数据转换至NEC(北向、东向、垂直)坐标系数据，具体转换过程如下：

BNEC=R(NEC←ITRF)·R(ITRF←ICRF)·R(ICRF←ASC)

·R(ASC←FGM)·BFGM，

(1)

其中R(ASC←FGM)为将FGM传感器参考系数据转换至卫星光具座(ASC)参考系数据，虽然角度在发射前已经确定，但在卫星运行过程中会不断变化，因此需要进行校正；R(ICRF←ASC)为将基于level-2的卫星姿态数据由ASC参考系数据转换到国际天球参考系(ICRF)数据；R(ITRF←ICRF)为将ICRF参考系数据转换到国际地球参考系(ITRF)数据；R(NEC←ITRF)为将ITRF参考系数据转换到NEC参考系数据.

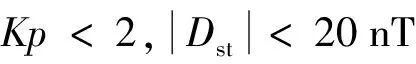
本文拟计算并分析2010.0年(2010年1月1日)的中国及邻近区域地磁场分布，研究范围为18°N—54°N,73°E—136°E.为了获得均匀且高密度分布的卫星数据，通过试验，发现对于某一时间点前后60天内的卫星数据经归算后可获取较为理想的测点分布，然而由于测点的分布并不均匀，考虑到每个测点在三维建模中的权重应一致，因此对归算后的所有数据进行网格化处理.现选取2010.0年作为研究时间点，将该时间点前后60天内的数据进行归算，以经纬度1°为间隔，在每个格点处取其上下左右1°内所有卫星数据的平均值进行网格化.对剩余较少的缺测格点，则进行分段线性插值.最后得到在中国及邻近地区的卫星网格值，共为2368个数据点.2010年为CHAMP卫星观测末期，卫星轨道高度较初期有所下降，2010.0年所有CHAMP卫星数据的高度约为302.59～312.84km.

图1为背景网格数据的平面分布图，每个数据格点都均匀分布.图2为网格数据的三维分布，从低纬到高纬地区，数据点高度呈下降趋势.现基于这些网格数据建立三维Taylor模型.

2.2 Taylor多项式模型

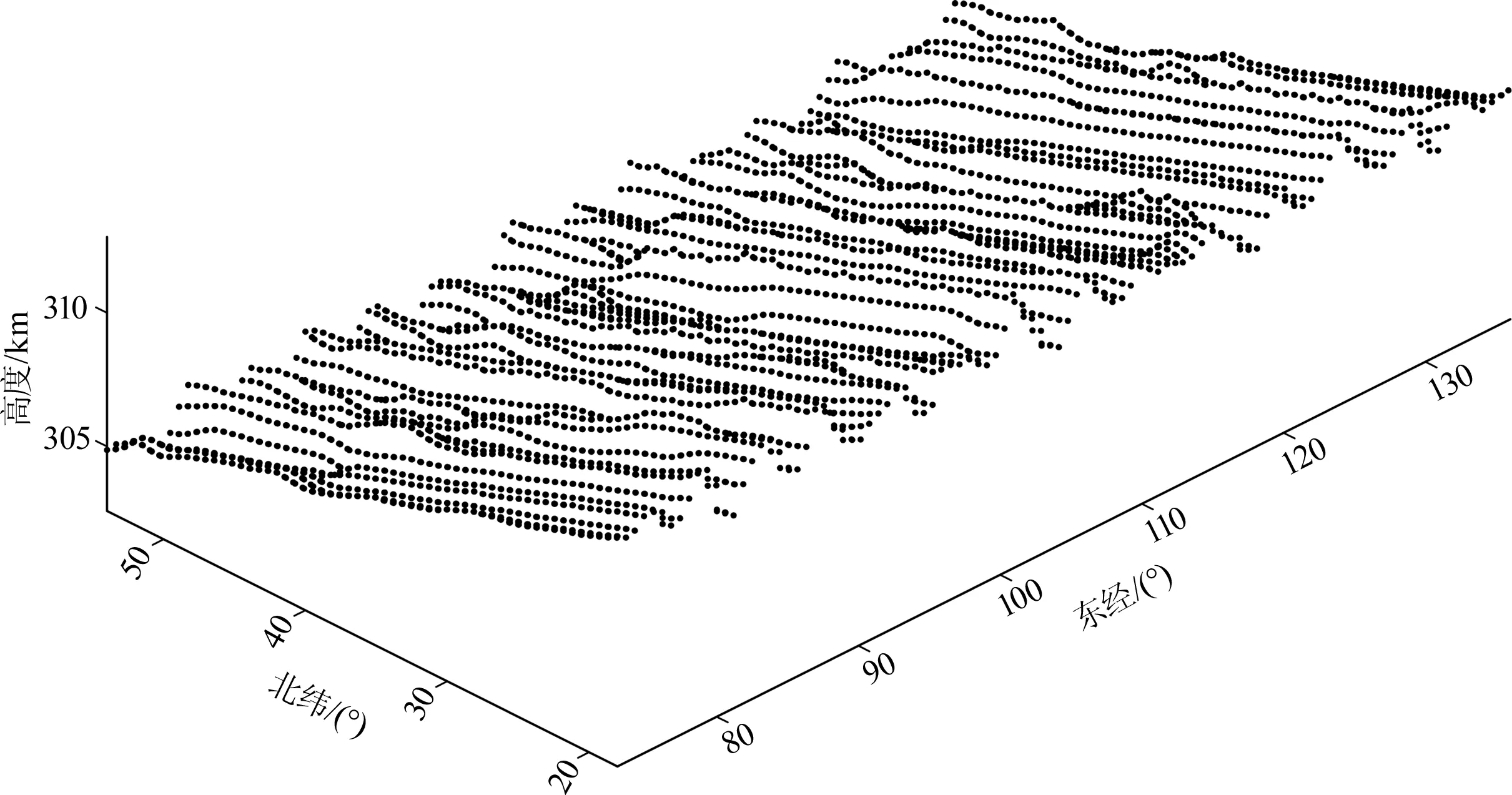
图2 CHAMP卫星磁场数据的三维分布Fig.2 Three-dimenson distribution of CHAMP satellite magnetic data

本研究基于二维Taylor多项式模型建立三维Taylor多项式模型.二维模型表达式如下：

(2)

上式中W表示任意磁场要素；N为截断阶数；φ,λ为各地磁测点的纬度和经度；φ0,λ0为多项式的展开原点，φ0=36°N,λ0=104.5°E；Aij为相应各分量的模型系数，每个模型有N(N+1)/2个系数，所有系数通过最小二乘法求取.

(2)式的系数为一下三角矩阵，该系数展开称为经典展开，而更为普遍的方法为进行完整展开(方阵展开)，这样做的优点是可以较低的截断阶数反映出更多的地磁场信息，后文会有所阐述.现基于二维模型，通过添加高度项，并通过系数的完整展开而得到三维Taylor模型，其表达式如下：

(3)

上式中W表示任意磁场要素，N为截断阶数；φ,λ,h为各地磁测点的纬度、经度和高度；φ0,λ0,h0为多项式的展开原点，φ0=36°N，λ0=104.5°E，h0=302.59～312.84 km；Aijk为模型系数，每个模型有N3个系数，所有系数通过最小二乘法求取.

3 结果

3.1 截断阶数的选取

Taylor多项式模型为基于数据点的拟合模型，截断阶数的选取非常重要.过低的截断阶数可能会导致区域地磁场短波长信息的丢失，从而使模型无法展示高精度区域地磁场的时空分布，而过高的截断阶数在增加计算量的同时，还会使结果出现局部畸变.

通常根据如下两条依据以确定合适的截断阶数(安振昌，2001)：

(1)区域地磁场模型的均方偏差要小于IGRF的均方偏差；

(2)随着截断阶数的增加，RMSE逐渐减小，当RMSE趋于稳定时，可确定截断阶数.

RMSE通过下式计算得到：

(4)

其中，Wmod为任意地磁要素的模型值，Wobs为相同地点同一地磁要素的观测值，n为观测点数量.

现根据式(4)计算各阶三维模型的RMSE值，结果见表1．

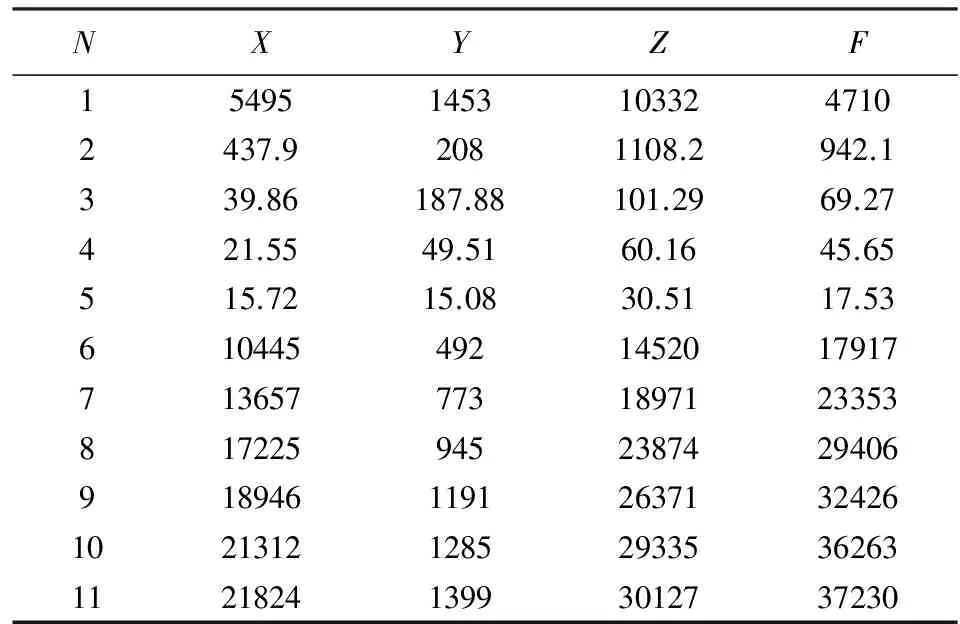
表1 三维Taylor多项式模型各截断阶数的RMSE(单位：nT)

根据表1，基于CHAMP卫星数据的三维Taylor多项式模型的RMSE值在N≤5时，X、Y、Z、F分量的RMSE随N的增大而迅速减小，平均下降幅度达到了65.18%，其中X分量由1阶的5495 nT减小为5阶的15.72 nT，Y分量从1阶的1453 nT减少为5阶的15.08 nT，Z分量从10332 nT减少为30.51 nT，F总量由4710 nT减小为17.53 nT；当N>5时，三维模型的RMSE值大幅增加，X分量为10445 nT，Y分量为492 nT，Z分量为14520 nT，F总量为17917 nT.这是由于阶数过高而导致的区域异常现象，即“龙格现象”.

根据第一条选取依据，现基于最新发布的IGRF12计算了其与实测点数据的RMSE值(见表2).

表2 实测点与IGRF12的RMSE值(单位：nT)Table 2 The RMSE values between measuring points and IGRF12(units: nT)

根据表1和表2，当2≤N≤5时，三维模型的RMSE值小于IGRF12的RMSE值，即满足选取判据(1).综上，三维模型的截断阶数选为5.

3.2 中国及邻近地区的三维Taylor多项式模型的计算和分析

基于不同高度的CHAMP卫星网格点，利用5阶三维Taylor多项式模型计算2010.0年的中国及邻近地区地磁场网格值.模型原点为研究区域的中心，即φ0=36°N，λ0=104.5°E.基于所得系数绘制的卫星高度处X、Y、Z、F四个要素的三维分布见图3．

根据图3，X分量的强度随着纬度的升高而逐渐减小，由34140.77 nT(18°N,59°E)左右减少为14823.98 nT(54°N,73°E)左右，等值线走向基本与纬度方向一致.Y分量的分布略为复杂，大致呈π型分布，强度自西向东逐渐减小，最大值为西北部(54°N,73°E)处的2449.25 nT左右，最小值在东北部(49°N,135°E)处的-3527.66 nT左右.Z分量的等值线走向基本与纬度方向一致，强度随着纬度的升高而增大，由低纬度12349.70 nT(18°N,136°E)左右上升到高纬度49657.99 nT(54°N,99°E)左右.地磁场F总量的分布与Z分量类似，强度随着纬度的升高而增大，最大值为51884.40 nT(54°N,104°E)左右，最小值为33647.11 nT(18°N,136°E)左右.由于采用的是卫星网格数据，因此不存在边界效应.

为了比较验证所建模型，基于相同的CHAMP卫星数据，对所有高度都取平均值，即h0=307.69 km.通过输入每个测点在h0处的经纬度及X、Y、Z和F总量的强度值，利用二维Taylor模型计算并绘制了中国及邻近地区的地磁场分布(未列出).当N≥5时，二维模型的RMSE值逐渐趋于平稳，下降并不明显.考虑到截断阶数越高，计算量越大，且两种模型在相同阶数时反映的信息量不同.通过RMSE值的比较，现认为5阶的三维Taylor模型与8阶的二维Taylor模型都能达到满意的模拟精度，其精度接近(后文有详细阐述).比较发现两种模型所得到的4要素地磁场无论在分布还是强度上均非常相似，故不再将二维模型的图形列出.

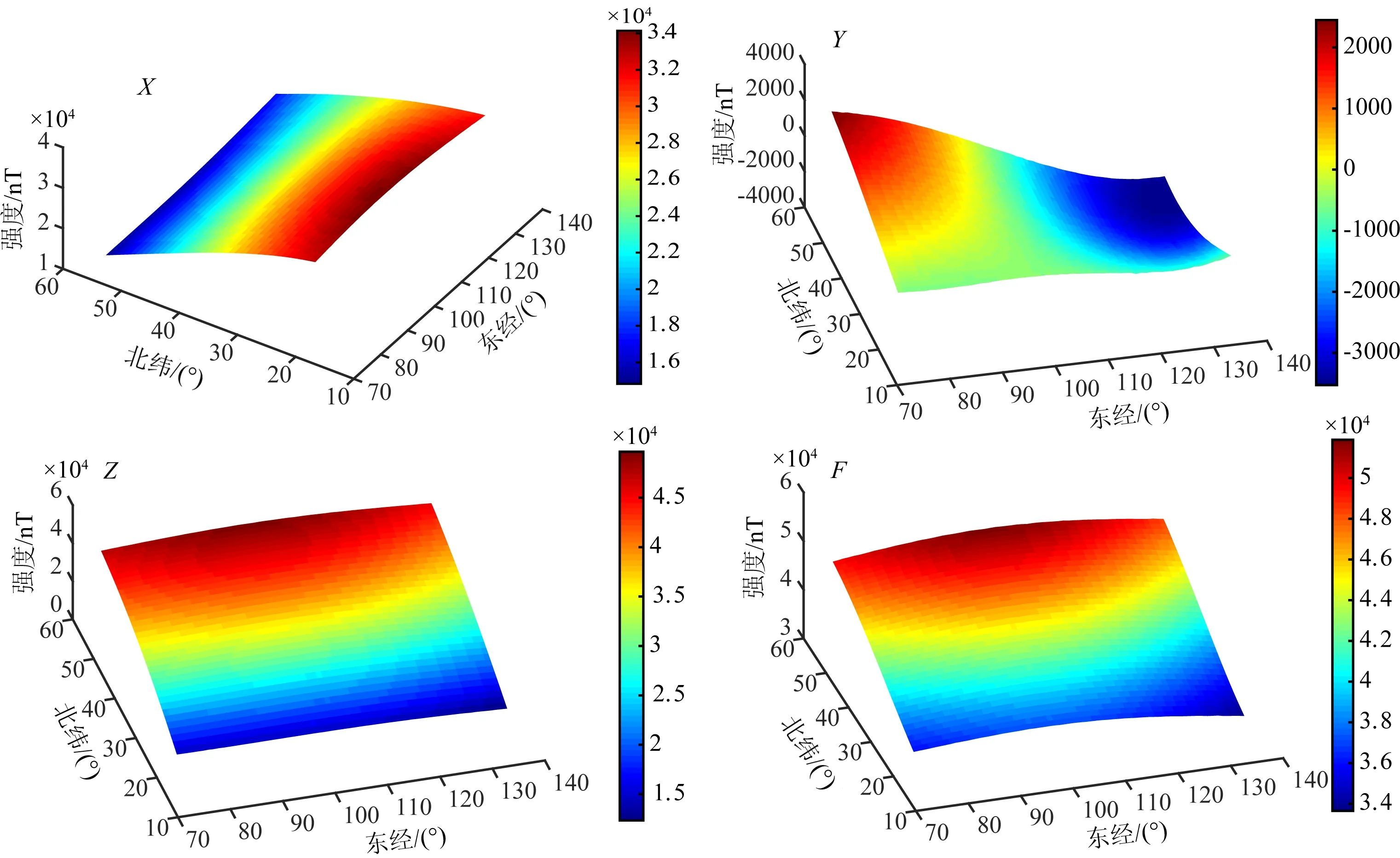
图3 基于5阶三维Taylor多项式模型的中国及邻近地区地磁分布(高度：302.59～312.84 km)；单位：nTFig.3 Geomagnetic distribution of China and its adjacent regions based on 3D Taylor polynomial model with degree 5(altitude: 302.59～312.84 km); units: nT

为了比较所建模型的拟合效果，现将部分测点的实测值及其8阶二维模型和5阶三维模型值进行对比(见图4).

根据图4，两种模型的拟合值与实测值非常接近，图中两条线基本重合，而Y分量则存在一些差异，从与实测值的接近程度及变化趋势看，三维模型拟合值要略好于二维模型拟合值.通过比较，可以发现每个实测点的二维以及三维模型值与对应实测数据的平均误差为1%.

然而，二维模型是一种平面方法，所有数据点都要求在同一水平高度上.因此二维模型所使用的平均高度(307.69 km)与本文数据(302.59～312.84 km)相比就会存在±5 km左右的高度差，由此而产生的误差是不可避免的，并且对于二维模型是无法计算这部分误差的.而三维模型的结果不仅考虑了高度的因素而且能与实测值很好的拟合.因此总体而言，三维模型的拟合效果是令人满意的.

为了进一步地观察两模型的差异，现绘制了两种模型相对于实测值的残差分布图(见图5).

通过比较发现，两种模型绘制的残差网格图无论在分布以及强度上都很接近.并在各分量的一些正负残差分布位置都较为相似，如X分量在塔里木盆地的约30 nT的正残差分布和内蒙古中部的约-40 nT的负残差分布、Y分量在中国地区东经110°附近约-33 nT的负残差分布、Z分量在广西南部约-70 nT的负残差分布以及F总场量在漠河一带约40 nT的正残差分布都很相似.

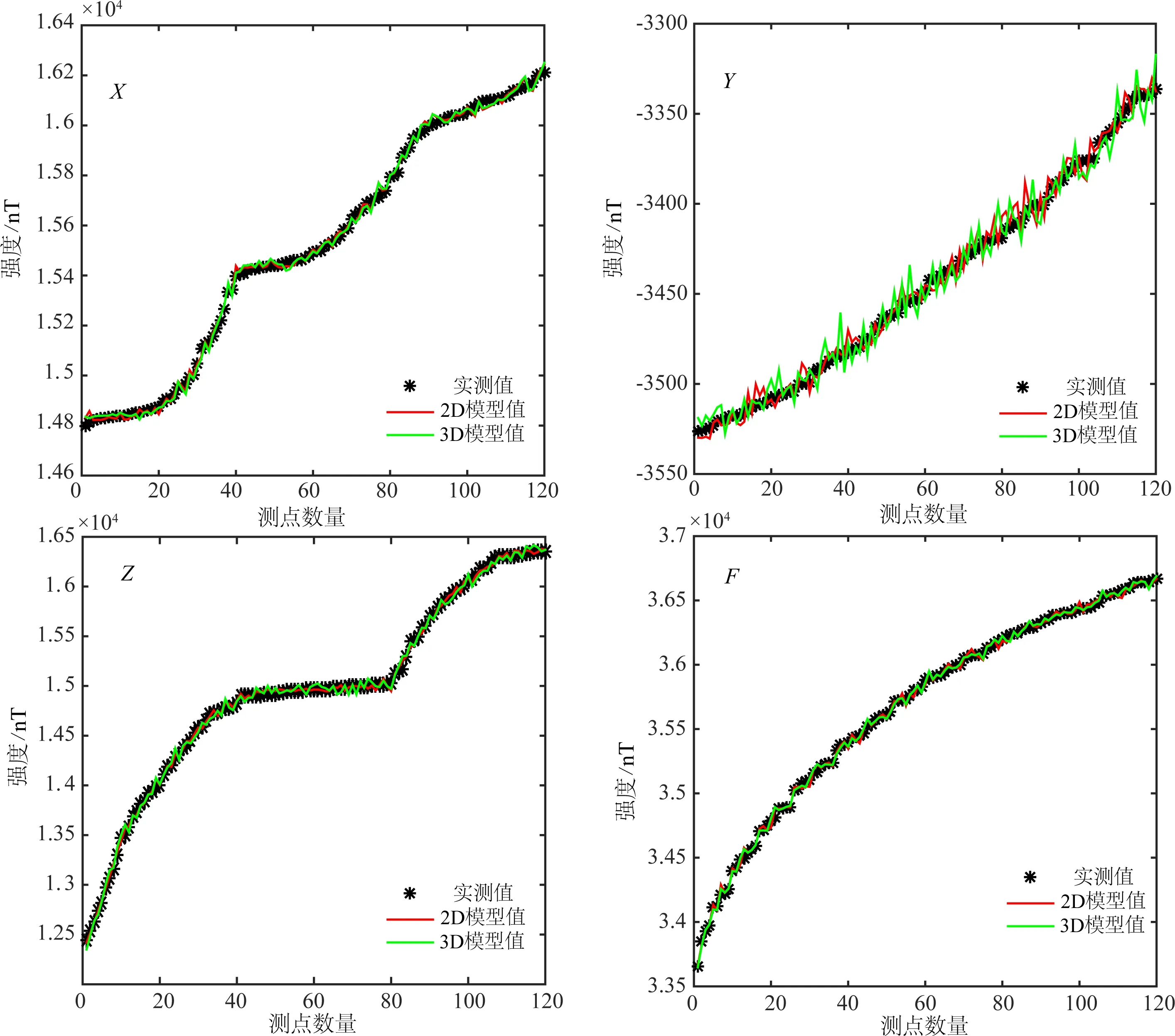
图4 三维模型和二维模型的模拟值与实测值的比较；单位：nTFig.4 The comparison among observed values and their modelling values based on 3D and 2D model; units: nT

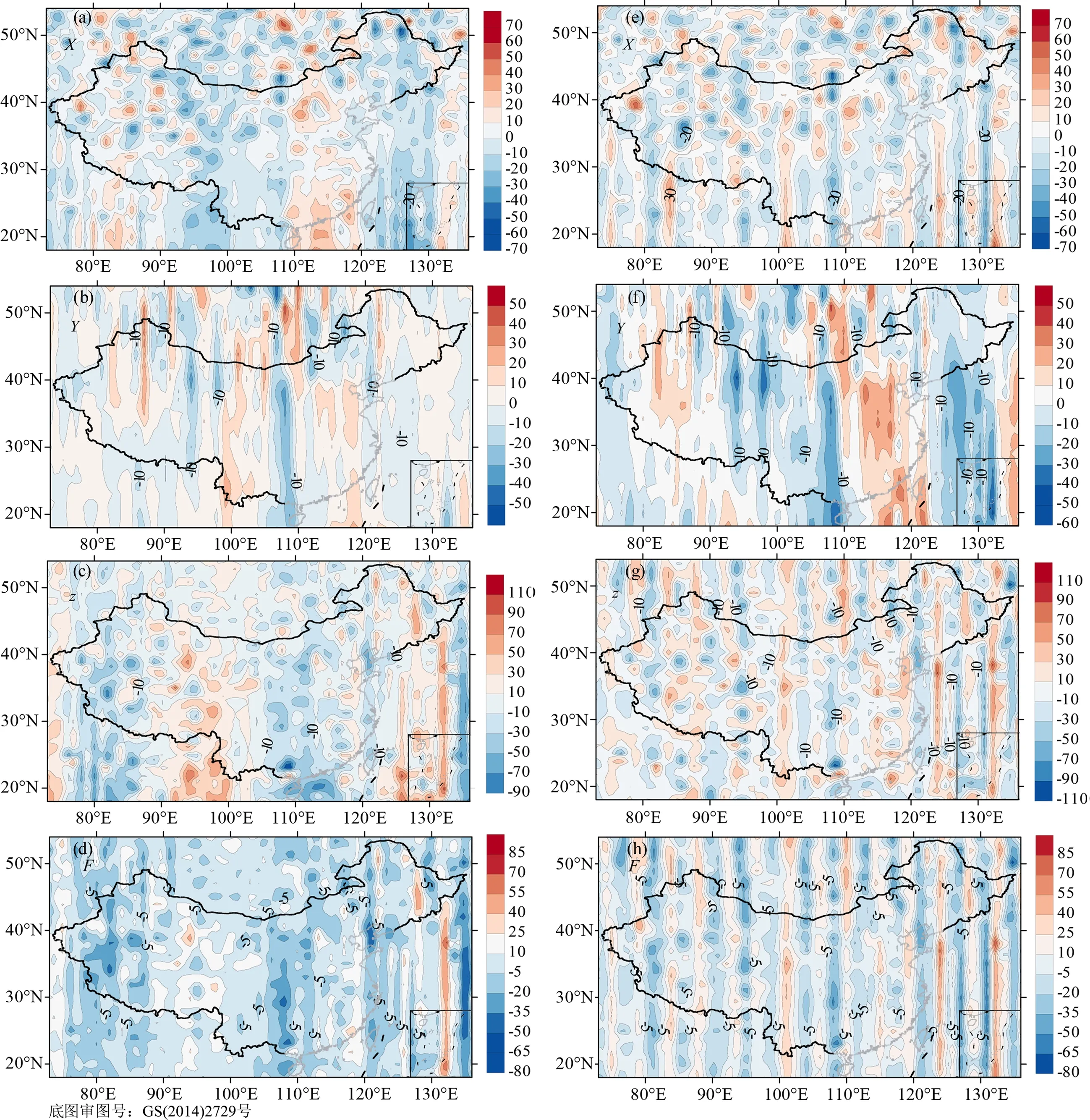
图5 三维模型(左)和二维模型(右)的残差分布图；(a—d) X,Y,Z,F；(e—h) X,Y,Z,F；单位：nTFig.5 The residual distribution of 3D model (left) and 2D model (right); (a—d) X,Y,Z,F；(e—h) X,Y,Z,F; units: nT

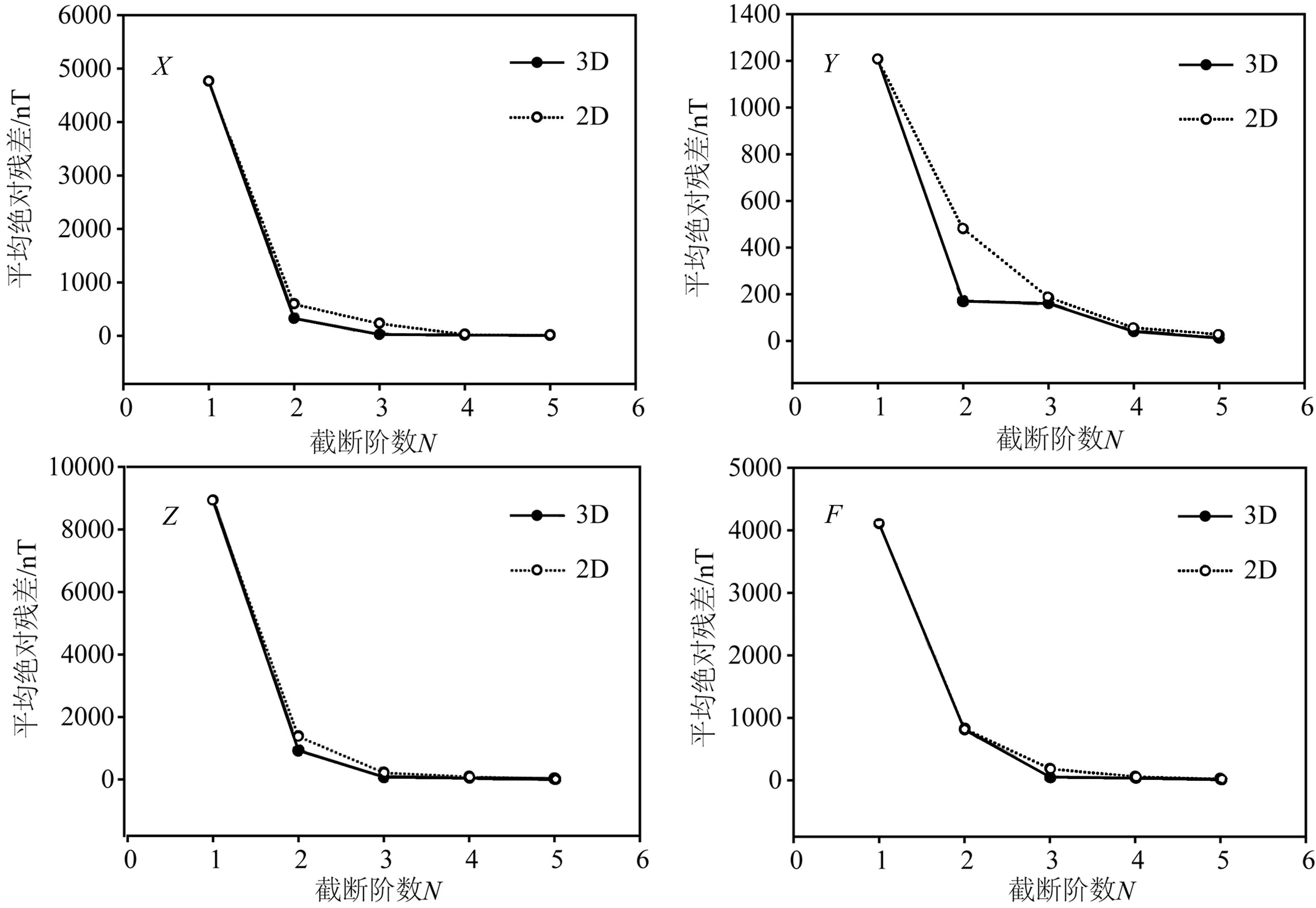
图6 三维模型和二维模型的残差绝对值的平均值变化Fig.6 Mean values variation of absolute residual of elements X, Y, Z, F based on 3D and 2D model; units: nT

以上两种分布的比较很难发现明显的区别，为了更为直观地观察两种模型的拟合效果，计算了两模型相对于所有CHAMP卫星网格数据的残差.比较发现两模型的残差在变化幅度上相差不大，但对于X分量和F总量，三维模型要明显优于二维模型.三维模型的残差整体要小于二维模型，如三维模型X分量的平均相对误差为0.051%，要小于二维模型的0.054%，三维模型F总量的平均相对误差为0.031%，要小于二维模型的0.043%，下降了0.012%.

为了进一步说明两种模型的差异，通过下式计算两种模型N为1～10时的残差绝对值的平均值变化，上式中Rm为所有点残差绝对值的平均值，其他各变量的意义与(4)式相同.

(5)

图6列出了两模型在N为1～5时的残差绝对值求平均的结果.根据图6可知，随着N的增加，三维模型的平均残差的下降速度要略快于二维模型的，在N相同的情况下，三维模型的平均残差要比二维模型平均小45.09%，这说明了相同阶数三维模型的拟合精度要好于同阶的二维模型.

下面对于两模型的RMSE进行分析.首先列出了二维模型在N为1～11时的RMSE变化(见表3).

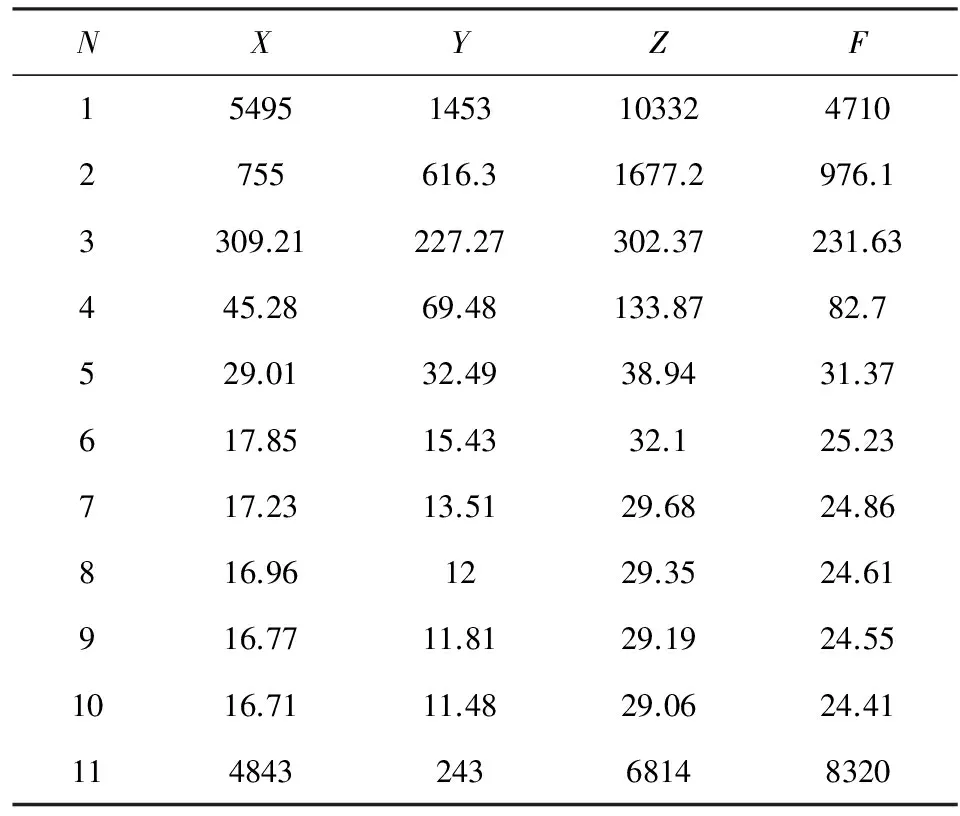
表3 二维Taylor多项式模型各截断阶数的RMSE(单位：nT)Table 3 The RMSE of each truncation order of 2D Taylor polynomial model (units: nT)

根据表3，基于CHAMP卫星数据的二维Taylor模型在截断阶数N<6时，X、Y、Z、F分量的RMSE随N的增大而迅速减小，平均下降幅度达到了60.62%，其中X分量由1阶的5495 nT减小为6阶的17.85 nT，Y分量从1阶的1453 nT减少为6阶的15.43 nT，Z分量从10332 nT减少为32.10 nT，F总量由4710 nT减小为25.23 nT；当N为6～10时，RMSE平均减少幅度为2.96%，逐渐趋于平稳；当N>10时，二维模型也出现了“龙格现象”，RMSE值大幅增加.

为了进一步比较，绘制了两模型当N=1～11时的RMSE变化(见图7).由图7可知，当N为1～5时，三维模型的RMSE值均小于二维模型，当N=5时，三维模型中X分量和F总量的RMSE值都要远小于8阶二维模型的X分量和F总量，而Z分量与7～10阶的二维模型值非常接近，三维模型的5阶Y分量则略大于8阶的二维模型.综合考虑磁场分布、残差分布以及RMSE的比较，现认为5阶的三维Taylor模型与8阶的二维Taylor模型具有相近的精度，且在X分量和F总量上三维模型的精度甚至更高.

通过比较发现，三维模型在N为1～5时RMSE值比对应的二维模型平均要小45.8%，另外根据两种模型的系数个数，认为在基于CHAMP卫星数据以模拟中国地区地磁场的情况下，较低阶的三维模型可反映更多的地磁场信息，其精度相当于高阶的二维模型.

为了进一步观察两模型，并考虑到存在的差异，列出了N=3时两模型的系数，见表4，表5.

图7 二维及三维Taylor多项式模型的RMSE随截断阶数N的变化；单位：nTFig.7 The relationship between RMSE and N of elements X,Y,Z,F in 2D and 3D Taylor polynomial model; units: nT

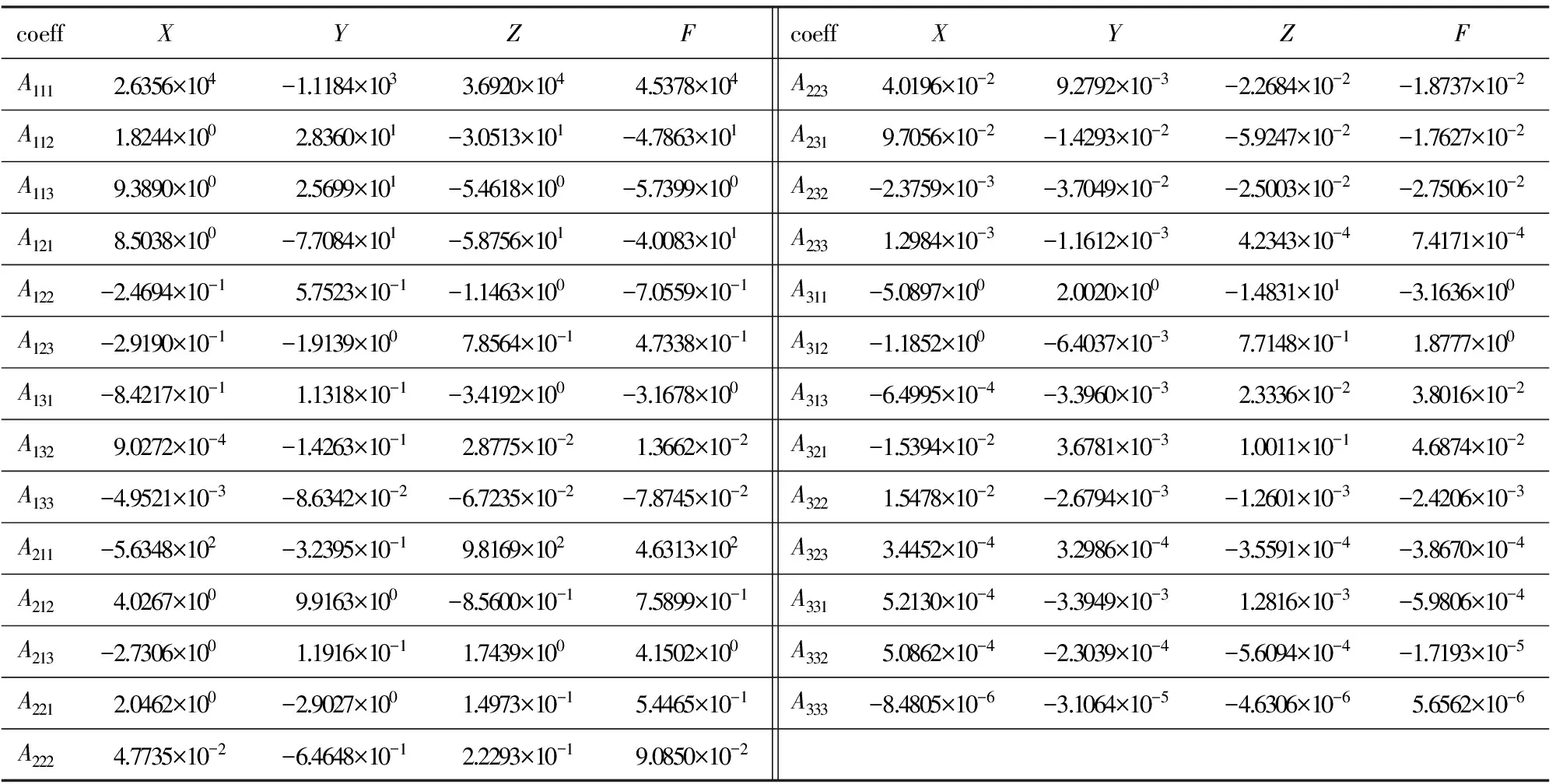
表4 3阶三维Taylor多项式模型系数Table 4 The coefficients of 3D Taylor polynomial model while N is 3

表5 3阶二维Taylor多项式模型系数Table 5 The coefficients of 2D Taylor polynomial model while N is 3

由表4和表5可知，两种模型在第一项系数上非常接近，而且在数值上比其他项系数大2到3个数量级，因此两种模型在拟合结果以及分布都非常接近.相比于二维模型，三维模型的系数个数约为二维模型的4倍，地磁模型的系数能反映地磁场强度等信息，如IGRF模型中各阶系数能反映偶极子场和各阶非偶极子场的强度信息，当N>13，认为球谐模型的系数即反映了不同波长所对应的岩石圈磁场的强度信息.Taylor多项式模型的各阶系数从地球物理的角度而言，应包含了区域地磁场不同尺度的强度信息，但由于其为区域模型，并不具备正交性，因此是很难从功率谱的角度定量地分析不同尺度的区域地磁场与不同阶系数的关系，故三维模型具备更多系数的具体含义，也是以后工作中需要考虑的问题.

4 结论与讨论

本文基于CHAMP卫星的网格数据运用三维Taylor多项式模型计算并绘制了2010.0年中国及邻近地区的地磁场分布，并通过对比，分析了两种模型的残差分布、截断阶数与RMSE等.结果显示5阶的三维Taylor模型与8阶的二维Taylor模型具有相近的精度.通过比较两种模型的拟合值、残差分布，截断阶数与RMSE值等，显示三维模型都要优于同阶的二维模型，并认为较低阶的三维模型可以得到与高阶二维模型相近，甚至更好的拟合效果，并得出以下结论：

(1)相较于其他二维模型，如二维Taylor多项式模型、曲面Spline等，三维Taylor模型考虑了高度因素，在中国及邻近地区，海拔高度为-4～8 km左右，而地磁场一般随高度呈20 nT/km左右的速率衰减，因此三维Taylor模型相较于二维模型有了本质的提高.本研究使用了高精度、高密度的CHAMP卫星的标量和矢量数据，基于此建立的中国地区三维模型，相较于IGRF11、甚至球冠谐模型，不仅计算方便，而且精度相当甚至更高.

(3)本研究显示了较低阶数的三维模型，其RMSE与较高阶数的二维模型接近，通过比较两种模型不同截断阶数对应的RMSE值、以及磁场和残差分布，认为三维模型每一阶的RMSE和残差绝对值的平均值均要比二维模型的小约45%.

通过计算还发现二维模型的边界畸变很大，而三维模型的边界效应相对较小.原因在于，在完整展开的三维模型中，我们取的截断阶数为N不是很大，“龙格现象”尚未得以发展(柳士俊等，2011).

二维Taylor模型只考虑了经度与纬度，忽略了高度的因素.因此二维模型由于本身的限制，所计算的地磁场强度会存在一定的误差.针对上述缺点，结果显示三维模型可以更准确地描述地磁场的空间分布.之所以采用完整展开，是因为可在较少的截断阶数计算出更多的系数，从而提高效率.

由于缺乏2010.0年的地面实测数据，因此研究只展示了卫星高度处的地磁场分布，今后若可获取地面及海洋地区，甚至航磁数据，可尝试从不同高度联合建立三维Taylor多项式模型，该模型的空间适用范围为地面至卫星高度，因此适合进行空间磁场的应用研究.若结合T04(Tsyganenko and Sitnov，2005)、CM4等模型，可进一步模拟区域外源场以及岩石圈磁场的形态分布(冯彦等，2010b；2014b).综上所述，三维Taylor模型具有计算简单、使用方便、且具有相当的模拟精度，适于进行区域三维地磁场的研究.

致谢 感谢空间天气学国家重点实验室开放课题以及德国地球科学研究中心对本文提供的帮助.

Alldredge L R. 1981. Rectangular Harmonic analysis applied to the Geomagnetic field.J.Geophys.Res., 86(B4): 3021-3026.

Alldredge L R. 1982. Geomagnetic local and regional Harmonic analyses.J.Geophys.Res., 87(B3): 1921-1926.

An Z C, Xu Y F, 1981. Methods of computation of geomagnetic field at greater altitude in a local region.ChineseJournalofSpaceScience. (in Chinese), 1(1): 68-73.

An Z C, Xu Y F, Xia G H, et al. 1982. Mathematical method to express the distribution of geomagnetic field and its secular variation in a local area.ActaGeophysicaSinica(in Chinese), 25(S): 711-717.

An Z C, Xu Y F, Wang Y H. 1991a. Derivation and analysis of the main geomagnetic field models in China for 1950—1980.ActaGeophysicaSinica(in Chinese), 34(5): 585-593.

An Z C, Wang Y H, Xu Y F. 1991b. Calculations and analyses of vertical gradient of the geomagnetic field in China and adjacent areas.ChineseJournalofSpaceScience(in Chinese), 11(1): 14-23.

An Z C. 2001. Analyses and discussions of the geomagnetic field polynomial models.ChineseJ.Geophys. (in Chinese), 44(S): 45-50, doi: 10.3321/j.issn:0001-5733.2001.z1.007.

Chen B, Gu Z W, Gao J T, et al. 2011. Analyses of geomagnetic field and its secular variation over China for 2005.0 epoch using Spherical Cap Harmonic method.ChineseJ.Geophys. (in Chinese), 54(3): 771-779. doi:10.3969/j.issn.0001-5733.2011.03.017.Düzgit Z, Baydemir N, Malin S R C. 1997. Rectangular polynomial analysis of the regional geomagnetic field.Geophys.J.Int., 128(3): 737-743.

Feng Y, An Z C, Sun H, et al. 2010a. Geomagnetic survey satellites.ProgressinGeophysics(in Chinese), 25(6): 1947-1958. doi: 10.3969 /j.issn. 1004-2903. 2010.06.009.

Feng Y, An Z C, Sun H, et al. 2010b. Analysis of variation in geomagnetic field of Chinese mainland based on comprehensive model CM4.ActaPhysicaSinica(in Chinese), 59(12): 8941-8953.

Feng Y, Pan J J, An Z C, et al. 2010c. Calculation and analysis of geomagnetic field horizontal gradients in China.ChineseJ.Geophys. (in Chinese), 53(12): 2899-2906. doi:10.3969/j.issn.0001-5733.2010.12.013.

Feng Y, Jiang Y, Sun H, et al. 2014a. A study on variations of non-dipole magnetic field over Chinese mainland during 2000 BC to 1990 AD.ScienceChina(EarthSciences), 57(6):1229-1244. doi:10.1007/s11430-013-4674-6.

Feng Y, Sun H, An Z C, et al. 2014b. A study on lithospheric field based on geomagnetic model with high precision and power spectrum.ProgressinGeophysics(in Chinese), 29(2): 478-487. doi:10.6038/pg20140202.

Gao J T, An Z C, Gu Z W, et al. 2005. Selections of the geomagnetic normal field and calculations of the geomagnetic anomalous field.ChineseJ.Geophys. (in Chinese), 48(1): 56-62, doi: 10.3321/j.issn:0001-5733.2005.01.010.

Gao J T, An Z C, Gu Z W, et al. 2006. Distributions of the geomagnetic field and its secular variations expressed by the surface Spline method in China (a part) for 1900—1936.ChineseJ.Geophys. (in Chinese), 49(2): 398-407, doi: 10.3321/j.issn:0001-5733.2006.02.013.

Haines G V. 1985. Spherical cap harmonic analysis of geomagnetic secular variation over Canada 1960-1983.J.Geophys.Res., 90(B14): 12563-12574.

Hurwitzd L, Knapp D G, Nelson J H, et al. 1966. Mathematical Model of the Geomagnetic Field for 1965.J.Geophys.Res., 71(9): 2373-2383.IAGA, Working Group V-MOD. 2003. The 9th Generation International Geomagnetic Reference Field.PhysicsoftheEarthandPlanetaryInteriors, 140(4): 253-254.IAGA, Working Group V-MOD. 2005. The 10th Generation International Geomagnetic Reference Field.PhysicsoftheEarthandPlanetaryInteriors, 151(3-4): 320-322.

IAGA, Working Group V-MOD. 2010. International Geomagnetic Reference Field: the eleventh generation.Geophys.J.Int., 183(3): 1216—1230.

Kang G F, Gao G M, Bai C H, et al. 2009. Characteristics of the secular variation and secular acceleration distributions of the main geomagnetic field for the CHAMP satellite.ChineseJ.Geophys. (in Chinese), 52(8): 1976-1984, doi:10.3969/j.issn.0001-5733. 2009.08.004.

Kang G F, Gao G M, Bai C H, et al. 2010. Distribution of the magnetic anomaly of the CHAMP satellite in China and adjacent areas.ChineseJ.Geophys. (in Chinese), 53(4): 895-903, doi:10.3969/j.issn.0001-5733. 2010.04.014.

Liu S J, Zhou X G, Sun H, et al. 2011. The three dimension Taylor polynomial method for the calculation of regional geomagnetic field model.ProgressinGeophysics(in Chinese), 26(4): 1165-1174. doi:10.3969/j.issn.1004-2903. 2011.04.005.Maus S, Lühr H, Rother M, et al. 2007. Fifth-generation lithospheric magnetic field model from CHAMP satellite measurements.Geochem.Geophys.Geosyst., 8(5). doi:10.1029/2006GC001521.Olsen N, Lühr H, Sabaka T J, et al. 2006. CHAOS-a model of the Earth′s magnetic field derived from CHAMP, Ørsted, and SAC-C magnetic satellite data.Geophys.J.Int., 166(1): 67-75.

Olsen N, Mandea M, Sabaka T J, et al. 2010. The CHAOS-3 geomagnetic field model and candidates for the 11th generation IGRF.EarthPlanetsandSpace, 62(10): 719-727.Sabaka T J, Olsen N, Purucker M E. 2004. Extending comprehensive models of the Earth′s magnetic field with Ørsted and CHAMP data.Geophys.J.Int., 159(2): 521-547.

Thébault E, Schott J J, Mandea M, et al. 2004. A new proposal for spherical cap harmonic modelling.Geophys.J.Int., 159(1): 83-103. doi:10.1111/j.1365-246X.2004.02361.x.

Thébault E, Schott J J, Mandea M. 2006. Revised spherical cap harmonic analysis (R-SCHA): Validation and properties.J.Geophys.Res., 111(B1): B01102, doi:10.1029/2005JB003836.Thébault E, Gaya-Piqué L. 2008. Applied comparisons between SCHA and R-SCHA regional modeling techniques.Geochem.Geophys.Geosyst., 9(7): Q07005, doi:10.1029/2008GC001953.Thébault E. 2008. A proposal for regional modelling at the Earth′s surface. R-SCHA2D.Geophys.J.Int., 174(1): 118-134. doi: 10.1111/j.1365-246X.2008.03823.x.

Tsyganenko N A, Sitnov M I. 2005. Modeling the dynamics of the inner magnetosphere during Strong geomagnetic storms.J.Geophys.Res., 110(A3): A03208. doi:10.1029/2004JA010798.Xu W Y, Tschu K K. 1984. A study of the RHA for the geomagnetic field of China and neighbouring region.ActaGeophysicaSinica(in Chinese), 27(6): 511-522.

Xu Y F, Wang Y H, An Z C. 1992. An analysis and the models of the geomagnetic secular variation in China for 1950—1985.ActaGeophysicaSinica(in Chinese), 35(6): 740-747.

Yang Y T, Shi Z Y, Guan Z Z, et al. 2009. A method of improving regional geomagnetic field model boundary effect.ProgressinGeophysics. (in Chinese), 24(2):468-474, doi: 10.3969/j.issn. 1004-2903.2009.02.013.

附中文参考文献

安振昌, 徐元芳. 1981. 局部地区高空磁场的计算方法. 空间科学学报, 1(1): 68-73.

安振昌, 徐元芳, 夏国辉等. 1982. 表示局部地区地磁场及其长期变化分布的数学方法. 地球物理学报, 25(增刊): 711-717.

安振昌, 徐元芳, 王月华. 1991a. 1950～1980年中国地区主磁场模型的建立及分析. 地球物理学报, 34(5): 585-593.

安振昌, 王月华, 徐元芳. 1991b. 中国及邻近地区地磁垂直梯度的计算与研究. 空间科学学报, 11(1): 14-23.

安振昌. 2001. 地磁场多项式模型的分析与讨论. 地球物理学报, 44(增刊): 45-50, doi: 10.3321/j.issn:0001-5733.2001.zl.007.

陈斌, 顾左文. 高金田等. 2011. 2005.0年代中国地区地磁场及其长期变化球冠谐和分析. 地球物理学报, 54(3): 771-779, doi: 10.3969/j.issn.0001-5733.2011.03.017.

冯彦, 安振昌, 孙涵等. 2010a. 地磁测量卫星.地球物理学进展, 25(6): 1947-1958, doi:10.3969/j.issn.1004-2903.2010.06.009.

冯彦, 安振昌, 孙涵等. 2010b. 利用地磁场综合模型CM4分析中国大陆地区地磁场变化. 物理学报, 59(12): 8941-8953.

冯彦, 潘剑君, 安振昌等. 2010c. 中国地区地磁场水平梯度的计算与分析. 地球物理学报, 53(12): 2899-2906, doi:10.3969/j.issn.0001-5733.2010.12.013.

冯彦, 孙涵, 安振昌等. 2014b. 基于高精度地磁模型与功率谱技术的岩石圈磁场研究. 地球物理学进展, 29(2): 478-487, doi:10.6038/pg20140202.

高金田, 安振昌, 顾左文等. 2005. 地磁正常场的选取与地磁异常场的计算. 地球物理学报, 48(1): 56-62, doi: 10.3321/j.issn:0001-5733.2005.01.010.

高金田, 安振昌, 顾左文等. 2006. 用曲面SPLINE方法表示1900—1936年中国(部分地区)地磁场及其长期变化的分布. 地球物理学报, 49(2): 398-407, doi: 10.3321/j.issn:0001-5733.2006.02.013.

康国发, 高国明, 白春华等. 2009. CHAMP卫星主磁场长期变化和长期加速度的分布特征. 地球物理学报, 52(8): 1976-1984, doi: 10.3969/j.issn.0001-5733.2009.08.004.

康国发, 高国明, 白春华等. 2010. 中国及邻近地区CHAMP卫星磁异常的分布特征. 地球物理学报, 53(4): 895-903, doi: 10.3969/j.issn.0001-5733.2010.04.014.

柳士俊, 周小刚, 孙涵等. 2011. 用于区域地磁场模型计算的三维Taylor多项式方法. 地球物理学进展, 26(4): 1165-1174, doi:10.3969/j.issn.1004-2903. 2011.04.005.

徐文耀, 朱岗昆. 1984. 我国及邻近地区地磁场的矩谐分析. 地球物理学报, 27(6): 511-522.

徐元芳, 王月华, 安振昌. 1992. 1950—1985年中国地磁长期变化的模型和分析. 地球物理学报, 35(6): 740-747.

杨云涛, 石志勇, 关贞珍等. 2009. 一种改善区域地磁场模型边界效应的方法. 地球物理学进展, 24(2): 468-474, doi: 10.3969/j.issn.1004-2903.2009.02.013.

(本文编辑 胡素芳)

Regional geomagnetic modelling based on the magnetic data of CHAMP satellite and 3D Taylor polynomial

JIANG Yong1,2, JIANG Yi1, FENG Yan1,2*, LIU Bao-Jia1,FU Shuai1, CHANG De1, ZHANG Peng-Fei1, JIANG Tao1

1InstituteofSpaceWeather,NanjingUniversityofInformationScienceandTechnology,Nanjing210044，China2StateKeyLaboratoryofSpaceWeather,ChineseAcademyofSciences,Beijing100190,China

The inherent shortcoming of most regional models is the lack of altitude information. In order to overcome this, the objective of this study is to establish the three-dimensional (3D) model of elementX,Y,Z, andFover Chinese and its adjacent regions in 2010.0 at the height of about 300 km. Based on the vector and scalar geomagnetic measuring data of CHAMP satellite, associated with 3D Taylor polynomial method, we try to create the 3D model over China and calculate the spatial distribution of geomagnetic field region. 3D model not only has the advantages like simple calculation and convenient to use, but also takes into account the height. In addition, the selection of truncation level of 3D model was also discussed. In order to verify the constructed 3D model, a comparison between 3D and Taylor polynomial (2D) model was taken, we analyzed the Root-mean-square error (RMSE) and the residual distributions between 3D and 2D models in different truncation level.Results showed RMSE and the mean absolute residuals of each level of the 3D model are about 45% smaller than that of 2D model. The 3D model of degree 5 basically has the same precision as that of 2D model of degree 8 in this study. Geomagnetic distributions and residuals of 3D and 2D models have high consistency. After comparing with 2D model, the 3D model considers the altitude information, so the precision is really improved; the coefficients show that 3D model of low degree can reflect more information and has the similar precision when compared to 2D model of high degree.

Geomagnetic model; 3D Taylor polynomial; CHAMP satellite; Root-mean-square error

蒋勇， 姜乙， 冯彦等. 2015. 基于CHAMP卫星与三维Taylor多项式模型的区域地磁建模研究.地球物理学报，58(9):3121-3132,

10.6038/cjg20150909.

Jiang Y, Jiang Y, Feng Y,et al. 2015. Regional geomagnetic modelling based on the magnetic data of CHAMP satellite and 3D Taylor polynomial.ChineseJ.Geophys. (in Chinese),58(9):3121-3132,doi:10.6038/cjg20150909.

10.6038/cjg20150909

P318

2015-03-13，2015-07-30收修定稿

国家自然科学基金(41404053，41174165)，公益性行业(气象)科研专项(GYHY201306073)，江苏省高校自然科学研究基金(14KJB170012)以及大学生创新创业训练计划项目基金联合资助.

蒋勇，主要从事数值模拟及空间天气建模方面的研究.E-mail：jianguk@163.com

*通讯作者 冯彦，男，1980年生，博士，讲师，研究方向：地磁场建模以及地磁场与空间天气的关系.E-mail:frank_feng8848@163.com