海潮误差对GRACE时变重力场解算的影响研究

王长青， 许厚泽， 钟敏*， 冉将军， 周江存

1 中国科学院测量与地球物理研究所大地测量与地球动力学国家重点实验室， 武汉 430077 2 中国科学院大学， 北京 100049



海潮误差对GRACE时变重力场解算的影响研究

王长青1,2， 许厚泽1， 钟敏1*， 冉将军1， 周江存1

1 中国科学院测量与地球物理研究所大地测量与地球动力学国家重点实验室， 武汉 430077 2 中国科学院大学， 北京 100049

海潮误差是 GRACE 时变重力场反演中重要的误差源，目前发布的海潮模型中主要包含振幅较大的主潮波分量模型，在时变重力场反演中次潮波的影响也是不可忽略的，因此，GRACE 时变重力场反演中的海潮误差主要包括受限于海潮模型误差和次潮波影响.本文利用轨道模拟方法检测了短周期潮波的混频周期以及次潮波对ΔC20, ΔC30的时序特征，并进一步通过轨道模拟结果分析了海潮误差对时变重力场反演的影响，然后通过实测数据解算分析了海潮误差对当前 GRACE 时变重力场解算的影响，研究发现：(1) 利用轨道模拟能够有效地检测短周期潮波的混频周期；(2)时变重力场解算过程中，次潮波的影响大于海潮模型误差的影响；(3)海潮模型误差以及次潮波影响是当前 GRACE 没有达到基准精度的重要因素之一.

GRACE； 时变重力场反演； 轨道模拟； 海潮混频周期； 次潮波

1 引言

在GRACE时变重力场的反演中，海洋潮汐周期性的影响是通过目前可用的海潮模型从GRACE观测值中扣除，而模型中存在的误差会通过对轨道的扰动使时变重力场解算结果受到影响，并且在 GRACE 卫星轨道的采样周期作用下使得海潮误差变为具有一定周期的海潮模型混频误差.这种混频信号的周期从几天至几年不等，对于月尺度的 GRACE 时变模型小于一个月的假频周期通过月平均处理之后模型混频影响对GRACE结果影响不大，但大于 1 个月的混频周期的影响无法消除(Knudsen and Andersen, 2002)，并且长周期的混频误差对于 GRACE 时间序列分析，尤其是对量级较小的质量变化信号提取造成影响(Zou et al., 2010).

国内的学者讨论了海潮模型误差对 GRACE 卫星重力场测量的影响(周江存和孙和平，2007；赵倩等， 2011).国际上，Han等(2004)通过由海潮模型误差引起的重力位估计了潮波分量并考察了海潮模型混频误差对时变重力场造成的影响，Seo等(2008)使用该方法进一步对海潮模型分量的混频周期进行了检测，其结果与Ray等(2003, 2006)的理论结果相符，Ray等(2006)利用实测的 GRACE 数据对海潮模型混频误差进行了分析，同时有国际同行提出对于下一代的卫星重力场解算潮波参数联合估计以削弱海潮模型误差的影响(Pail et al., 2014).上述的研究分析主要是针对海潮模型中的主潮波造成的混频效应，而海潮模型误差的影响中除了有各潮波分量引入的误差外，另外一种误差是由于海潮模型的次潮波造成的，即当前的海潮模型不能够对所有潮波进行描述，通常在海潮模型中只包含主潮波，其他没有被包含在海潮模型中的潮波分量同样也会引起重力场混频误差.GRACE 项目组虽然在解算 RL05 时变重力场模型时均考虑了次潮波影响(Bettadpur, 2013;Dahle et al., 2013; Watkins, 2012)，但对次潮波在重力场解算中的影响并未在相关文献中进行讨论.

本文在研究中结合了轨道模拟和GRACE实测数据解算两种方式：轨道模拟利用不同的海潮模型中潮波分量之差，根据GRACE卫星的地面轨迹计算在该时刻大地水准面变化，从而通过获取的大地水准面变化根据球谐分析转化为对全球重力场系数的影响，计算中不需要进行最小二乘求解，因此，比Han等和Seo等(Han et al., 2004；Seo et al., 2008)采用海潮模型误差引起的重力位来估计海潮模型混频误差更加简单、高效；实测数据解算方面，类似于Ray等(Ray et al., 2006)采用的研究方法，通过使用不同的海潮模型分别解算出不同的重力场模型从而考察海潮模型误差对时变重力场的影响，不同之处在于实测数据的解算中考虑了次潮波对重力场解算的影响.结合上述两种数据处理方式，本文在以下方面进行研究：短周期潮波混频误差以及次潮波对大地水准面的影响；短周期混频误差以及次潮波影响的周期性检测；利用轨道模拟和实测数据考察海潮误差在时变重力场解算的影响.

2 海潮模型误差

随着卫星测高和流体动力学模型的不断精化，海潮模型精度也不断提高，但各海潮模型之间依然存在差异.本文选择FES2004、EOT08a以及EOT11a研究海潮模型误差，这些海潮模型空间分辨率均为1/8°.海潮模型FES2004相对于同时期的海潮模型(如CSR04，GOT00等)具有更好的表现，因此，该模型用于GRACE RL04时变重力场模型的解算(Savcenko, 2008；Savcenko, 2012).为了改进浅海区的海潮模型精度，Savcenko等(2008)以FES2004为参考模型通过调和分析结合多个卫星测高任务解算了EOT08a.在解算EOT11a海潮模型过程中，结合多任务测高系统时采用了更加合理的方差分量估计等处理，使得EOT11a在浅海区域的表现优于前两者(Savcenko, 2012).在我们的研究中将海潮模型对重力场的影响分为两个方面来考虑：(1)利用不同的海潮模型之差引起的误差作为海潮模型误差来研究海潮模型在重力场反演中的混频效应，即由模型误差引起.本文以海潮模型 FES2004 和 EOT08a 对应的周日潮、半日潮短周期潮波分量的差值作为相应潮波分量的海潮模型误差，考虑由周日潮、半日潮等短周期潮波分量引起的海潮误差混频影响. (2)海潮模型中除主潮波外，其他的潮波分量在重力场反演中造成的影响，即由次潮波引起.通常海潮模型只提供了量级较大的潮波或是主要的潮波分量，但是其他的小的潮波分量并没有包含在海潮模型中，这些小的潮波分量在精密的轨道定轨和精密重力场模型解算中往往也是不能忽略的.Rieser等(2012)利用EOT11a海潮模型中的18个主潮波分量，通过潮汐导纳理论插值了引潮位大于 2×10-4m2·s-2的238个次生潮波.实际上，每个次潮波都对应一个周期，且都会产生相应的混频误差，在本文研究中主要考察次生潮波对时变重力场解算的影响，故在此不针对单个次潮波混频误差进行讨论，而是对所有次潮波在时变重力场解算中的影响进行讨论.本节利用EOT11a 海潮模型中的238个次潮波研究次潮波对时变重力场的影响.

|.

(1)

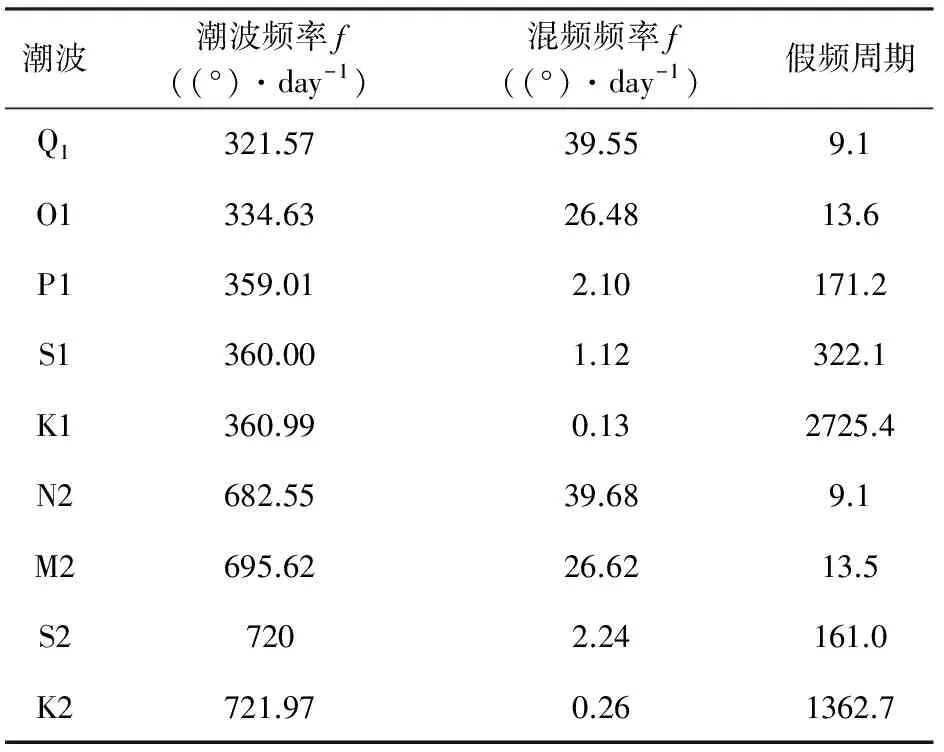
表1 短周期海潮模型以及相应的假频周期Table 1 Short period ocean tide models and their aliasing period

3 数据处理

3.1 轨道模拟

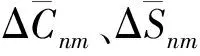
(2)

由海潮引起的地球上某一点的大地水准面变化ΔN(θ,λ)可以通过以下式子表达：

(3)

(4)

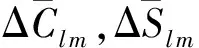
(5)

3.2 实测数据处理

低轨卫星在惯性系中的运动方程为

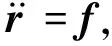
(6)

其中，f表示卫星受到的所有加速度之和，包括保守力加速度和非保守力加速度.保守力加速度的计算模型包括静态重力场模型、固体潮、海潮、极潮大气潮以及日月引力和大气海洋非潮汐质量变化等，GRACE卫星中装载高精度加速度计可获取非保守力.

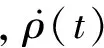
(7)

(8)

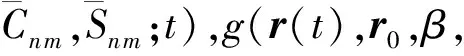
Δr(t) =r(t)-r0(t)

(9)

(10)

Nleo·x=bleo,

(11)

Nkbrr·x=bkbrr,

(12)

公式(11)、(12)中Nleo，Nkbrr分别为轨道观测和KBRR观测的法方程的信息矩阵，x为要待估参数，包括初始状态参数、加速度及参数以及时变重力场系数.根据各自数据的测量精度对上述法方程进行结合，即

(p·Nkbrr+Nleo)·x=p·bkbrr+bleo,

(13)

其中，p为KBRR数据与轨道观测数据的权比，本文中取值p=1×1010，每月所有弧段的法方程叠加并消去初始状态参数以及加速度参数后便可求得到该月份重力场系数.

为了考察海潮模型误差对时变重力场解算的影响，通过上述方法我们使用海潮模型FES2004、EOT08a 分别获取两个重力场模型，其他力模型不变(如表2)，那么两个重力场模型之间的差别便是由于海潮模型误差造成；为了考察次潮波的影响，我们先使用EOT11a海潮模型中的18个主潮波解算出一个重力场模型，然后再使用EOT11a 的256 个潮波(包括238个次潮波)获取另一个重力场模型，那么这两个模型之差便是由次潮波造成.

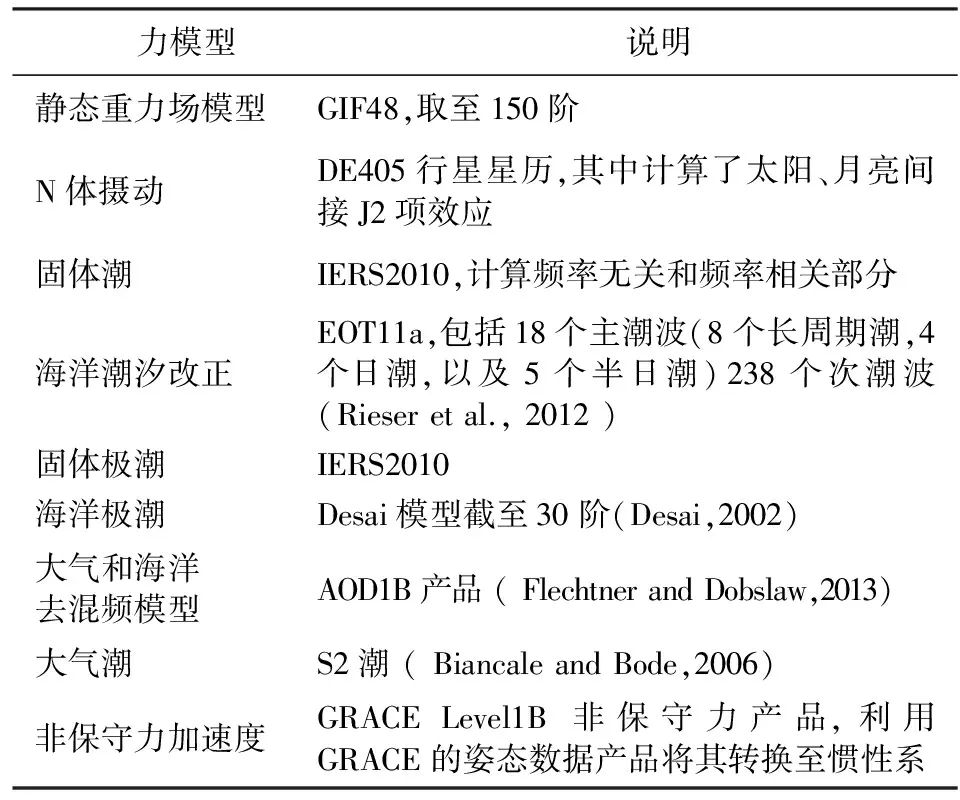
表2 重力场解算所用的力模型Table 2 Force models used for gravity field determination

4 结果分析

4.1 轨道模拟结果分析

利用GRACE A卫星数据按照上述轨道模拟方法计算了2006—2010年共5年的数据，首先我们对海潮模型误差造成的大地水准面变化进行分析.图1为2006年7月轨道模拟获取的8个短周期潮波(S2, K2,M2,N2,K1,P1,Q1,O1)混频误差以及由238个次潮波造成的以大地水准面变化表示的海潮模型误差空间分布.图中8个短周期潮波中，S2、K2、M2潮波分量误差造成的大地水准面变化具有较强的空间分布(注意图中的色度条)，且在信号强度上远大于其他的潮波分量.其中，S2、K2不同于其他的短周期潮波分量，没有表现出明显的条带特征；由238个次潮波造成的大地水准面变化在空间分布上表现出较强的条带特性，并且其量级相对于除S2外的其他短周期潮波具有更强的空间分布.

我们进一步分析了海潮模型误差对低阶球谐系数ΔC20, ΔC30的时间序列来检查8个短周期潮波分量造成的混频特性以及次潮波误差的时序特征.如图2中显示，由8个短周期潮波(图2(a—h))以及次潮波造成的ΔC20,ΔC30时间序列：S2、K2、P1的混频周期分别为163天、3.7年、171天，与表1的理论值相符.对于K1潮波分量，混频误差中存在长期趋势，本研究中使用的数据跨度小于K1的理论混频周期7.46年，因此无法检测出K1的混频周期，其他混频周期小于30天的潮波分量没有周期特性；次潮波误差对ΔC20、ΔC30造成的影响(如图2i)中包含有长期趋势项和约110天的周期，且长期趋势中可能含有大于5年的周期性误差.

从图1中可知，S2、K2、M2与238个次潮波误差造成的海潮误差具有较强的空间分布，进一步将其对大地水准面的影响换算成球谐系数，考察S2、K2、M2 和次潮波误差造成的海潮模型误差对重力场解算的影响.我们以获取的2006年7月时变重力场模型的精度表示当前 GRACE 的实测精度，以高于静态重力场模型GGM03C模型精度一个量级表示 GRACE 基准精度(Kim, 2000).从图中可以看出短周期潮波分量S2，K2的潮波分量误差分别在18阶、30阶以上超过了GRACE基准精度(图3中黑色曲线)，M2的模型误差影响相对较小，次潮波误差在 60阶范围内均超过基准精度.从图3可知，次潮波误差对重力场解算的影响大于海潮模型误差对重力场解算的影响.

图1 8个短周期潮波混频误差以及次潮波引起的海潮模型误差对大地水准面的影响Fig.1 Effects on geoid height induced by 8 short period ocean tides aliasing error and secondary tides error

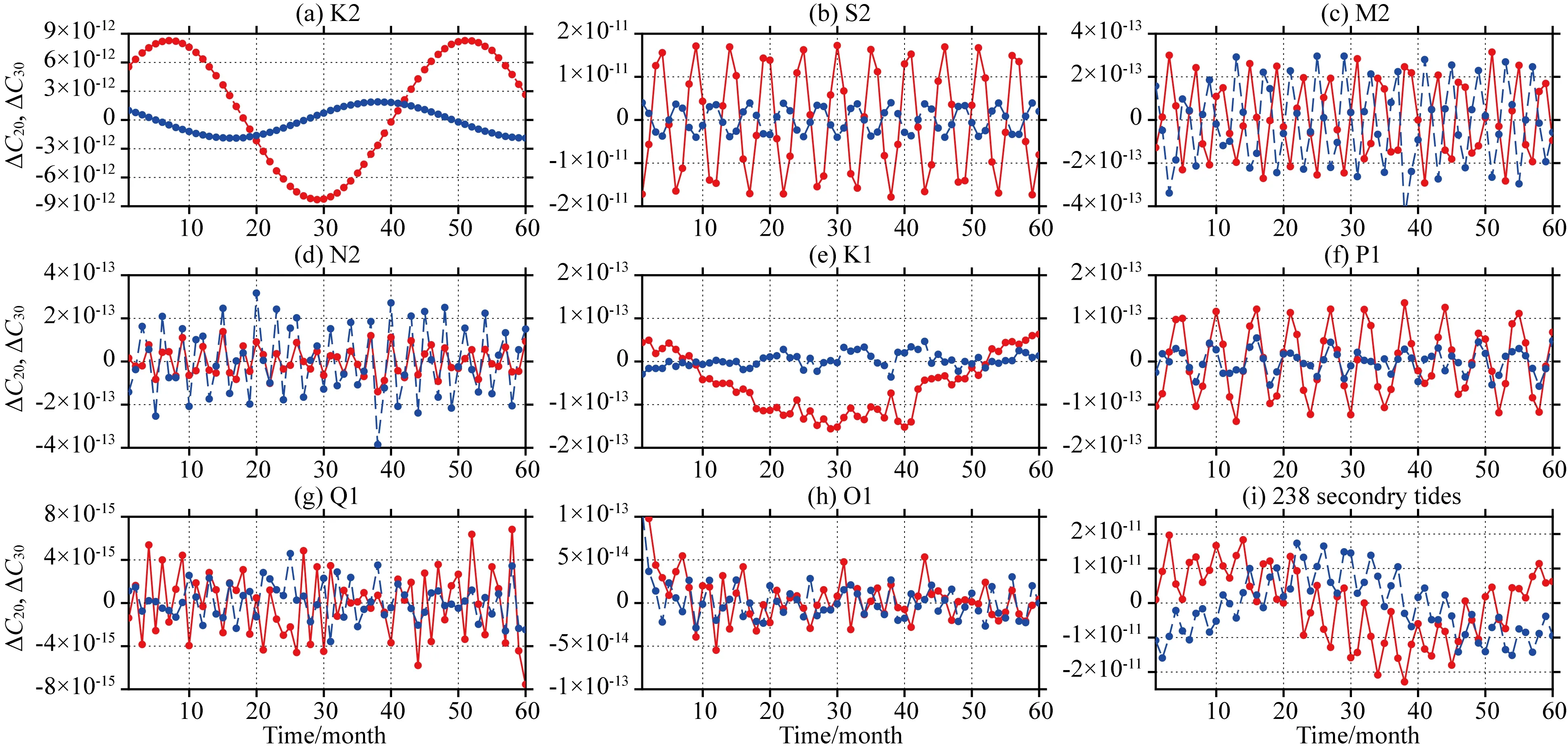
图2 8个短周期潮波混频误差以及次潮波误差造成的ΔC20,ΔC30时间序列对比图: 红色ΔC20，蓝色ΔC30Fig.2 Time series of ΔC20,ΔC30 induced by eight short ocean tides aliasing error and secondary error: red for ΔC20 and blue for ΔC30

4.2 实测数据解算结果分析

根据上述实测数据处理方法我们研究了海潮模型误差以及次潮波误差对实测数据的时变重力场解算的影响.研究中分别使用海潮模型FES2004、EOT08a进行重力场解算考察18个主潮波误差的影响，以及分别使用EOT11a中的18个主潮波、EOT11a 256个潮波(包括238个次潮波)考察次潮波误差对重力场解算的影响.对于GRACE卫星重力场解算，时变重力场精度的高低取决于KBRR残差中所包含的信噪比，在此我们首先分析不同的海潮模型对于KBRR残差的影响，图 4中显示了利用海潮模型FES2004、EOT08a时获取的KBRR残差RMS序列(图4a)以及利用EOT11a 18个主潮波以及EOT11a 256个潮波分量获取的KBRR残差RMS序列(图4b).利用海潮模型FES2004、EOT08a、EOT11a的18个主潮波以及EOT11a 256获取的该月的KBRR残差总的RMS分别为0.3365、0.3351 、0.3355、0.3275 μm·s-1.从图 4中可以看出,使用海潮模型FES2004、EOT08a获取的KBRR残差RMS差别不大，次潮波误差对KBRR残差RMS序列的影响大于前者.

我们进一步分析海潮模型误差以及次潮波误差对时变重力场解算精度的影响，图5是使用 FES2004、EOT08a、EOT11a(18个主潮波以及256个潮波)获取的时变重力场的每阶大地水准面高，其他力模型见表2.从图5中可以看出，使用不同海潮模型的18个主潮波获取的每阶大地水准面存在一定的差别，如图中曲线FES04_18、EOT08a_18以及EOT11a_18分别表示使用FES2004、EOT08a、 EOT11a海潮模型获取时变重力场模型的每阶大地水准面高.

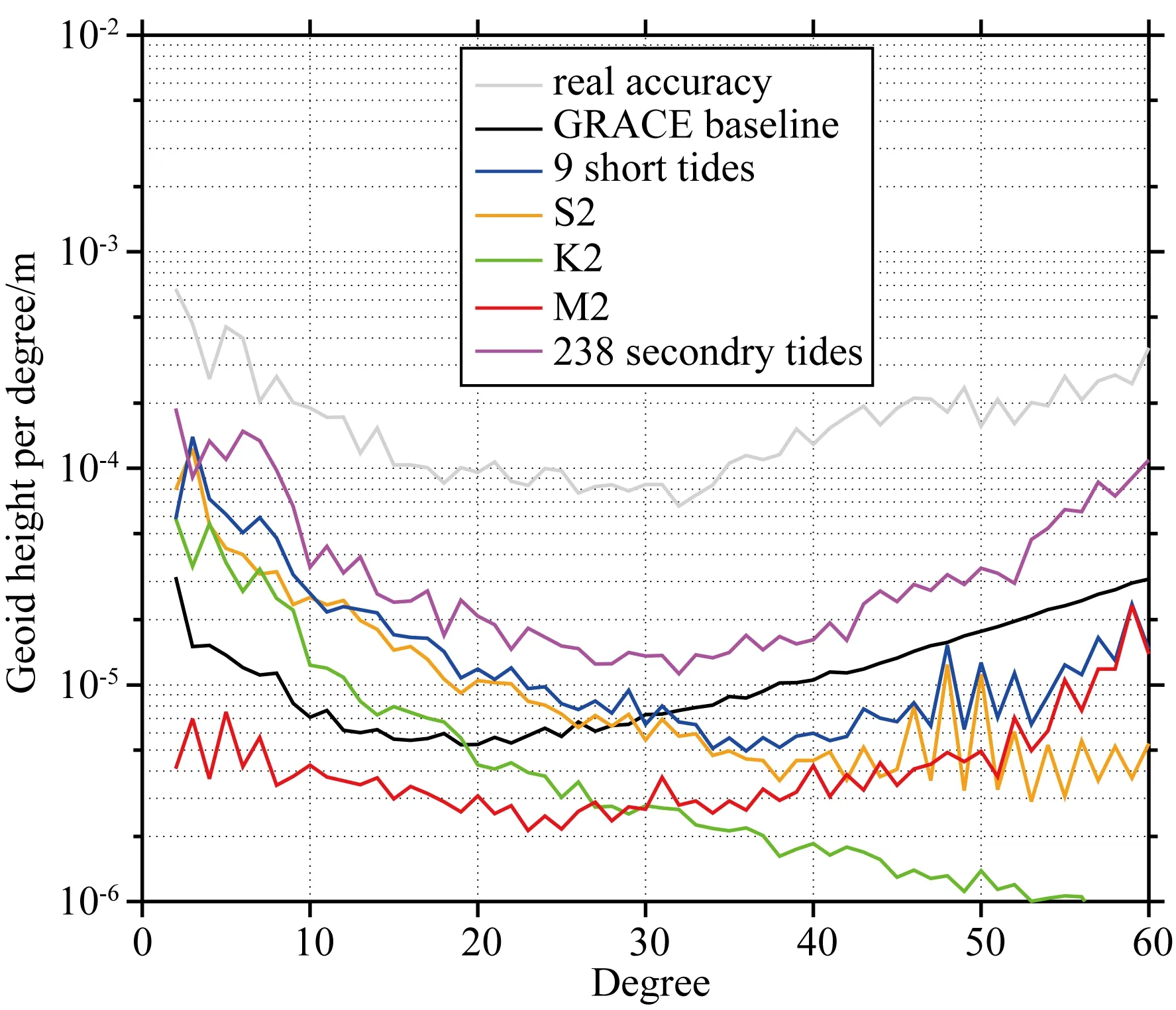
图3 轨道模拟获取的海潮误差造成对重力场解算的影响Fig.3 Effects of ocean tide error on temporal gravity field recovery using orbit simulation

使用次潮波时获取的每阶大地水准面(图5中EOT11a_256)比使用18个主潮波(图5中EOT11a_18曲线)获取的每阶大地水准面具有更高的精度.由EOT08a与FES2004海潮模型误差造成的对时变重力场反演的影响以图5中EOT08a-FES04曲线表示，由海潮模型的次潮波误差造成的对时变重力场反演的影响以图5中的Secondry tides曲线表示.从图中曲线看出，在时变重力场反演中海潮模型的次潮波造成的影响相比于海潮模型18个主潮波具有更强的影响.

进一步将图5与图3对比不难发现，通过实测数据获取的海潮模型误差以及次潮波对时变重力场的影响在20阶之前基本处于同一量级，20阶之后实测数据获取的结果要大于轨道模拟结果，这是因为在轨道模拟中不考虑误差的引入，但是在实测数据处理中由于各种误差的混合且误差并非表现为加性特征，随着解算阶数的增加各种混合误差更容易对重力场系数解算造成影响.因此，对于时变重力场解算的影响，轨道模拟结果在中高阶时被低估.

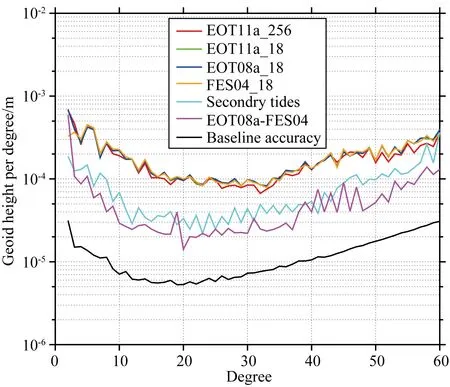
图5 实测 GRACE 数据获取的海潮误差对时变重力场解算的影响Fig.5 Effects of ocean tide error on temporal gravity recovery using real GRACE observation data

图4 不同的海潮模型获取的KBRR残差RMSFig.4 RMS of KBRR residuals using different ocean tide models

5 结论

本文通过轨道模拟和实测数据研究了海潮模型主潮波误差以及次潮波在重力场解算中的影响，利用轨道模拟结果分析了海潮模型短周期潮波误差以及次潮波对大地水准面的影响.分析显示S2、K2、M2潮波分量误差造成的大地水准面变化具有较强的空间分布，且S2、K2未表现出明显的条带特征，而次潮波误差造成的大地水准面变化具有更强的空间分布且表现出较强的条带特性.轨道模拟对于潮波分量混频周期的研究是一种简单有效的方法.使用轨道模拟对海潮模型混频周期检测结果显示，潮波分量K2、S2、P1的混频周期与理论值混频周期相符，通过轨道模拟发现238个次潮波对时变重力场的影响中包含有约110天的周期，并且可能存在大于5年的周期.通过轨道模拟分析以及实测观测数据对海潮模型误差、次潮波对时变重力场影响的对比分析表明，次潮波影响对时变重力场的影响大于海潮模型误差的影响，同时，综合分析对时变重力场解算结果的影响也表明，海潮模型误差以及次潮波的影响是当前 GRACE 没有到达基准精度的重要因素之一.随着海潮模型精度的不断提高，海潮模型误差对时变重力场造成的影响也会相应地减小，但海潮模型误差对于下一代卫星重力任务的影响还有待于我们的进一步研究；另一方面，将来的卫星重力任务将采用更高精度的测距系统(如GRACE-Follow on将配置激光测距系统)，因此，次潮波对星间距离测量的影响将更加敏感，对时变重力场的解算次潮波的影响将仍不可忽略.

致谢 感谢中国科学院测量与地球物理研究闫昊明研究员提供的GST数据分析软件，德国GFZ 提供的GRACE Level 1B数据，文中所涉图件由GMT软件绘制，在此一并表示感谢.

Bettadpur S. 2009. Recommendation for a-priori bias & scale parameters for Level-1B ACC data (version 2). GRACE Technical Note-02 Version 2. Bettadpur S. 2012. UTCSR Level-2 processing stands document for Level-2 product release 005. Center for Space Research, University of Texes at Austin. Biancale R, Bode A. 2006. Mean annual and seasonal atmospheric tide models based on 3-hourly and 6-hourly ECMWF surface pressure data. Potsdam: Deutsches Geo Forschungs Zentrum G F Z.ScientificTechnicalReport06/01, doi: 10.2312/GFZ.b103-06011.

Case K, Kruizinga G, Wu S. 2010. GRACE Level 1B data product user handbook. Jet Propulsion Laboratory, California Institute of Technology.

Dahle C, Flechtner F, Gruber C, et al. 2013. GFZ GRACE Level-2 processing stands document for Level-2 product release 005.ScientificTechnicalReport, doi: 10.2312/GFZ.b103-1202-25.

Desai S D. 2002. Observing the pole tide with satellite altimetry.J.Geophys.Res., 107(C11): 7-1—7-13, doi: 10.1029/2001JC001224. Flechtner F, Dobslaw H. 2013. AOD1B product description document for product release 05. GFZ German Research Centre for Geosciences.Han S C, Jekeli C, Shum C K. 2004. Time-variable aliasing effects of ocean tides, atmosphere, and continental water mass on monthly mean GRACE gravity field.J.Geophys.Res., 109(B4): B04403, doi: 10.1029/2003JB002501.Kim J. 2000. Simulation study of a low-low satellite-to-satellite tracking mission[Ph. D. thesis]. Austin: The University of Texas at Austin.

Knudsen P, Andersen O. 2002. Correcting GRACE gravity fields for ocean tide effects.Geophys.Res.Lett., 29(8): 19-1—19-4, doi: 10.1029/2001GL014005.

Pail R, Murböck M, Honecker J, et al. 2014. Treatment of ocean tide aliasing in the context of a next generation gravity field mission. // EGU General Assembly, Vienna, Austria.

Ray R D, Rowlands D D, Egbert G D. 2003. Tidal models in a new era of satellite gravimetry.SpaceScienceReviews, 108(1-2): 271-282.

Ray R D, Luthcke S B. 2006. Tide model errors and GRACE gravimetry: towards a more realistic assessment.Geophys.J.Int., 167(3): 1055-1059, doi: 10.1111/j.1365-246X.2006.03229.x. Rieser D, Mayer-Gürr T, Savcenko R, et al. 2012. The ocean tide model EOT11a in spherical harmonics representation. Technical Note. Savcenko R, Bosch W. 2008a. EOT08a-empirical ocean tide model from multi-mission satellite altimetry.DGFIreport, No. 81, 2008. Savcenko R, Bosch W. 2008b. EOT11a-empirical ocean tide model from multi-mission satellite altimetry.DGFIreport, No. 89, 2012.Seo K W, Wilson C R, Han S C, et al. 2008. Gravity Recovery and Climate Experiment (GRACE) alias error from ocean tides.J.Geophys.Res., 113(B3): B03405, doi: 10.1029/2006JB004747.Watkins M. 2012. JPL Level-2 processing stands document for Level-2 product release 005, Jet Propulsion Laboratory.

Zhao Q, Jiang W P, Xu X Y, et al. 2011. Analysis of influence of frequency aliasing effects on GRACE gravity solution.JournalofGeodesyandGeodynamics(in Chinese), 31(4): 123-126.

Zhou J C, Sun H P. 2007. Effect of ocean tide on recovery of satellite gravity field.ChineseJ.Geophys. (in Chinese), 50(1): 115-121. Zou Z B, Li H, Luo Z C, et al. 2010. Seasonal gravity changes estimated from GRACE data.GeodesyandGeodynamics, 1(1): 57-63.

附中文参考文献

赵倩, 姜卫平, 徐新禹等. 2011. GRACE卫星重力场解算中混频误差影响的探讨. 大地测量与地球动力学, 31(4): 123-126.

周江存, 孙和平. 2007. 海潮对卫星重力场恢复的影响. 地球物理学报, 50(1): 115-121.

(本文编辑 胡素芳)

A study on the effect of ocean tides error in GRACE temporal gravity field recovery

WANG Chang-Qing1,2, XU Hou-Ze1, ZHONG Min1*, RAN Jiang-Jun1, ZHOU Jiang-Cun1

1StateKeyLaboratoryofGeodesyandEarth′sDynamics,InstituteofGeodesyandGeophsics,ChineseAcademyofSciences,Wuhan430077,China2UniversityofChineseAcademyofSciences,Beijing100049,China

The ocean tides with periods of about 12 and 24 hours are rarely sampled by GRACE. The tidal signal and their errors can only be recognized after rather long “alias” periods. The ocean tide error is one of the error sources in GRACE temporal gravity field recovery. This paper aimed to study the effect of ocean tide error in GRACE temporal gravity field recovery. Generally, the ocean tide model released involves only the largest tides or main waves. However, the impact of secondary tides on temporal gravity field recovery cannot be negligible as well. Therefore, ocean tide errors in GRACE temporal gravity field recovery contain major wave′s error induced by accuracy level of ocean tide model and errors induced by secondary tides.Differences between the two ocean tide models (FES2004 and EOT08a) were used to estimate the magnitude of ocean tide model errors in this paper. Ocean tide model EOT11a with 18 major ocean tides and EOT11a with 238 secondary tides (plus 18 major ocean tides) were used to check the impact of 238 secondary tides on temporal gravity field recovery. We performed two methods to achieve the above goals: the orbit simulation using GRACE GNV1B products and the real GRACE recovery of monthly gravity solution using the variational equations approach. Based on orbit simulation, we analyzed the spatial distribution of tide model errors in terms of geoid height changes and time series of global spherical harmonic coefficient ΔC20and ΔC30induced by each of eight short period tide model errors and 238 secondary tides. Furthermore, we estimated the magnitude of ocean tide model errors and analyzed the impact of 238 secondary tides using the real GRACE recovery of monthly gravity solution.The analysis of the spatial distribution of ocean tide errors in terms of geoid height changes showed that ocean tide model errors in S2, K2 and M2 had significantly larger magnitudes than errors in other constituents. In addition, spatial distributions of tide model errors in S2 and K2 had long wavelength features and had no significant meridional strips. However, errors induced by 238 secondary tides had large amplitudes and significant meridional strips. Temporal alias errors obtained by orbit simulation analyses showed that alias periods of tide model errors in K2, S2 and P1 had an alias period of 3.7 years, 163 days and 171 days, respectively. These results coincided well with their theoretical values. What′s more, global spherical harmonic coefficient changes in ΔC20and ΔC30induced by 238 secondary tides mainly showed two different periods. The longer period might be larger than five years, and the shorter period was near 110 days. Orbit simulation results suggested that ocean tide model errors in S2 and K2 exceeded the GRACE baseline accuracy at degree larger than 30 and 18, and all nine short tide models′ error exceeded the GRACE baseline accuracy at degree 2～60. The results based on real GRACE observation data also indicated that the ocean tide model errors and the impact of secondary tides exceeded the GRACE baseline accuracy at degree 2～60. The analysis of orbit simulation and real GRACE recovery of monthly gravity solution suggested that the impact of secondary tide on temporal gravity field recovery was larger than ocean tide model errors.Based on the above investigations, we concluded that: (1)The orbit simulation can effectively detect alias periods of short period ocean tide model errors and also be used to check time series properties of the global spherical harmonic coefficients induced by secondary tides; (2) The impact of secondary tides on the current GRACE temporal gravity field recovery is greater than that of 18 major ocean tide model errors; (3) Ocean tide errors, including ocean tide model errors and the impact of the secondary tides, are important factors why current GRACE does not reach the GRACE baseline accuracy.

GRACE; Temporal gravity field recovery; Orbit simulation; Ocean tide alias period; Secondary tides error

王长青， 许厚泽， 钟敏等.2015.海潮误差对GRACE时变重力场解算的影响研究.地球物理学报，58(9):3072-3079,

10.6038/cjg20150905.

Wang C Q, Xu H Z, Zhong M, et al. A study on the effect of ocean tides error in GRACE temporal gravity field recovery.ChineseJ.Geophys. (in Chinese),58(9):3072-3079,doi:10.6038/cjg20150905.

10.6038/cjg20150905

P223

2015-01-15，2015-06-30收修定稿

国家重大科学研究计划(2013CB733305,2012CB957703)，国家自然科学基金(41174066,41131067，41374087，41431070，41374025)联合资助.

王长青，男，1985年生，在读博士研究生，主要从事时变重力场反演研究.E-mail:whiggsdkd@asch.whigg.ac.cn

*通讯作者 钟敏，男，1964年生，博士生导师，研究员，主要从事动力大地测量和时变重力场研究.E-mail:zmzm@whigg.ac.cn