美国Cove Fort-Sulphurdale地热区地震震源机制和各向异性研究*

张 佩 张海江, 刘 影王 华 M.Nafi Toksöz

1) 中国合肥230026中国科学技术大学地球和空间科学学院 2) 中国合肥230026中国科学技术大学地震与地球内部物理实验室 3) 美国剑桥02139麻省理工学院地球资源实验室



美国Cove Fort-Sulphurdale地热区地震震源机制和各向异性研究*

1) 中国合肥230026中国科学技术大学地球和空间科学学院 2) 中国合肥230026中国科学技术大学地震与地球内部物理实验室 3) 美国剑桥02139麻省理工学院地球资源实验室

Cove Fort-Sulphurdale位于美国犹他州中西部， 是一个地质特征独特的地热资源富集区． 为了有效开发地热资源， 有必要了解该地区的应力分布和裂缝分布． 本文在前人工作的基础上使用地震资料， 利用波形匹配、 P波极性和横纵波振幅比联合约束反演的方法， 研究该地区地震的震源机制解; 同时结合该地区的横波分裂分析研究， 确定该地区的应力分布和断层/裂隙走向． 波形反演结果显示, 实际数据与模拟数据的波形匹配度非常高， 且二者的P波初动极性和横纵波振幅比也都非常相近． 由震源机制分析得出的断层面走向大部分趋于南北向， 与美国区域应力图显示的最大水平主应力指向(南北方向)， 具有较好的一致性， 符合目前研究对该地区的构造认知． 横波分裂分析结果也表明如果各向异性主要是由该地区的断裂构造所引起， 那么该地区的主要断层或裂缝的方向可能为南北向．

Cove Fort-Sulphurdale 震源机制 波形匹配 区域地震 横纵波振幅比 地热横波分裂 各向异性

Hefei230026，China2)LaboratoryofSeismologyandPhysicsofEarth’sInterior，UniversityofScienceand

TechnologyofChina，Hefei230026，China3)EarthResourcesLab，MassachusettsInstituteofTechnology，Cambridge，MA02139，USA

引言

随着社会经济的快速发展， 传统能源供需矛盾加剧， 其对环境的影响也越来越大. 基于国家能源结构调整、 节能减排和环境保护的需求， 新型无污染、 可持续的替代能源的发展势在必行． 地热资源作为新型能源， 在缓解能源矛盾和环境压力方面很有潜力． 我国地热资源丰富， 全球地中海—喜马拉雅地热带和环太平洋地热带贯穿我国西南地区和东南沿海(郑克棪， 潘小平， 2009； 张金华等， 2013)． 因此， 地热资源在我国具有广阔的开发利用前景， 对我国的能源结构调整、 环境保护和新型节能环保型社会的建立具有重要意义．

在地热资源勘探开发过程中， 断裂的探测和表征以及原位应力的确定是两个非常关键的方面． 如果在地热资源开采之前就能够确定地下断裂的三维分布形态和应力分布， 我们就可以评估和制定一个较合理的开采方案， 合理配置资源， 实现社会效益和经济效益的最优化． 本文以美国Cove Fort-Sulphurdal地热区的研究为例， 分析地震与区域断裂和应力分布等的关系， 为后续的开发利用提供参考， 同时对我国地热资源的勘探开发有所启示．

Cove Fort-Sulphurdale地热区位于美国犹他州的中西部， 是一个具有独特地质特征的地热资源富集区． 该地区是一个构造过渡区域， 其西部展布着广阔的盆地和拥有一系列伸展构造、 正断层和铲状断层的山脉， 东南部为变形和断裂较少的科罗拉多高原． Sulphurdale区域受塞维尔(Sevier)造山运动的影响， 发育了很多破裂和褶皱， 其主要形成于阿尔布-赛诺曼(Albian-Cenomanian)时期(DeCelles， Coogan， 2006)． 该地区深部地层构成为古生代变质岩、 中生代白云岩、 灰岩以及红层(Moore， Samberg， 1979)， 上覆晚中生代砾岩， 层间夹杂砂岩和黏土岩(Rossetal， 1982)． 上部覆盖着第三纪—第四纪凝灰岩和其它火山熔岩． 进一步研究发现， 在该地区浅层存在石英二长岩的浅成岩体(Ross， Moore，1985)． 图1为该地区的区域地质图和断层分布．

图1 Cove Fort-Sulphurdale地热区域的地质图(引自Steven， Morris， 1983)

Cove Fort-Sulphurdale是美国西部最大的地热异常区的一部分． 自1975年以来， 该地区逐渐建立起一个与地热勘探开发相关的数据库， 包括详细的区域地质、 地震、 重力、 磁法以及电阻率研究的结果． 根据地质研究已经勾划出地热系统主要的构造单元， 这些构造以及较活跃的微震活动都暗示着该地热异常区巨大的潜能． 对于地热开发来说， 一个很重要的方面即为确定开发区域的应力分布以及断层或者裂隙的分布如其走向等． 本文将综合利用该地区的地震震源机制信息和横波分裂信息， 确定Cove Fort-Sulphurdale地热区的应力分布和断层/裂隙走向． 首先利用波形匹配、 P波极性和横纵波振幅比联合约束反演的方法， 得出研究区域地震的震源机制解， 然后利用该震源机制解进行区域应力分析并给出断层的走向分布．

国内外许多研究人员使用多个地震震源机制解或断层面滑动方向来反演构造应力场． Bott(1959)最早提出利用断层面上的滑动方向数据推断断层所在区域驱动断层运动的平均构造应力张量； Gephart和Forsyth(1984)提出了震源机制应力反演(focal mechanism stress inversion, 简写为FMSI)方法， 用以求解应力场； 许忠淮和戈澍谟(1984)使用滑动方向拟合法反演地震区的应力场； 钟继茂和程万正(2006)提出了力轴张量计算法． 此外， 还有格点尝试法、 系统聚类分析方法等．

另外地壳中的各向异性分布也受区域应力场和断层走向的影响． 控制地壳中的各向异性分布主要有两种机制： 一种是结构引起的各向异性， 另一种是应力引起的各向异性(Boness， Zoback， 2004)． 研究地壳中的各向异性通常采用横波分裂分析方法． 所谓横波分裂是指横波在穿过各向异性介质时会发生分裂现象(Zhangetal， 2007； Liuetal， 2008)， 较先到达的是快横波， 较后到达的是慢横波， 二者之间的偏振方向近似相互垂直， 其到时差大小与各向异性强度有关． 例如对于走滑断层， 由于断层两侧的相对滑动可能在断层面附近形成与走向平行的节理面， 因此沿断层走向传播的横波速度大于垂直于断层走向传播的横波速度． 所以在这种情况下， 快波的极化方向与断层走向有关． 应力引起的各向异性是指地壳中存在的微小裂缝， 在最大水平主压应力的作用下会在与应力平行的方向上发生定向排列， 因此在平行于主应力的方向上， 横波的传播速度快． 在这种情况下， 则可以根据快波的极化方向确定主应力的方向(Crampin， 1984； Crampin， Atkinson， 1985)． 本文在对该区域地震震源机制分析的基础上， 结合横波分裂分析的结果， 期望能对Cove Fort-Sulphurdale地热区域的断裂和应力分布有更清晰的认识， 为以后的地热开发利用等提供可靠依据．

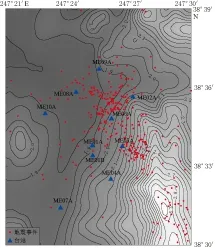
图2 Cove Fort-Sulphurdale地区的地震事件和台站分布 灰度代表地形高程(单位： km), 白色表示海拔高 Fig.2 Seismic events and stations distribution map in Cove Fort-Sulphurdale Red dots denote seismic events and blue triangles indicate stations， grayscale represents the terrain elevation (in km) (white indicates high altitude)

1 资料和方法

1.1 数据

为了更好地表征Cove Fort-Sulphurdale地区的速度结构及地质构造， 探究该地区的地震活动性， 美国麻省理工学院的一个研究组在此布设了一个由10个地震台站(ME01A， ME01B， ME02A， ME03A， ME05A， ME06A， ME07A， ME08A， ME09A和ME10A)组成的临时地震台网． 该地震台网工作了一年， 监测到几百个地震事件， 本文所使用的就是该台网记录到的地震数据． Cove Fort-Sulphurdale地区的地震台站和地震事件分布如图2所示．

1.2 方法

确定震源机制的传统方法是基于地震到达不同台站的直达P波极性信息或振幅信息． 但是对于Cove Fort-Sulohurdale研究区域， 由于台站分布稀疏， 单纯依靠这些信息难以确定可靠的地震震源机制． 为了克服这一困难， 我们除了利用直达P波的极性以及P、 S波振幅信息外， 还利用地震波的全波形信息． 这里我们采用Li等(2011)发展的基于网格搜索的全波形匹配方法确定震源机制． 下面对该方法进行简单介绍．

地震震源机制可以用一个3×3的二阶矩张量表示(Stein， Wysession， 2003)． 震源破裂过程中若介质没有发生旋转， 张量则为对称张量， 所以只有6个完全独立的分量． 假设地震事件的震源机制可以用单纯的双力偶源表示(Rutledge， Phillips， 2002)， 尽管实际上震源机制还可能包含体变和补偿线性向量偶极部分， 但是将震源机制限定为双力偶源有很多益处． 例如， 如果介质存在各向异性， 在确定震源机制时却基于各向同性介质假设， 则可能会导致在震源机制确定中引入虚假的非双力偶成分． 如果将震源机制限定为双力偶源， 这些由于未考虑各向异性而引起的假的非双力偶成分就可以被消除， 而双力偶成分可以被很好地恢复(ilen，uk， 2002)． 本文中用走向、 倾角和滑动角来表征震源机制， 并通过这3个参数确定双力偶源矩张量的各个分量． 对于矩张量的每个分量， 采用离散波数方法(Bouchon， 1981， 2003)计算其格林函数． 该方法设定地震与台站之间的结构可以用一维层状介质模型来表示． 对于已知矩张量的某个震源(即走向、 倾角、 滑动角已知)， 其在某个台站的理论地震波形可以表示为格林函数的加权线性组合， 即

(1)

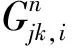
为了搜寻到最优解， Li 等(2011)建立了一个表征观测与模拟数据之间匹配度的目标函数． 该目标函数包含了地震记录波形信息的4个不同方面， 表示为

(2)

通常情况下， 横波(S波)振幅会比纵波(P波)振幅大很多． 为了平衡纵横波的贡献， 我们需要先将其分开， 类似于常用的CAP(cut and paste)方法(Zhu， Helmberger， 1996； 郑勇等， 2009； 谢祖军等， 2012)． 通过利用基于程函方程有限差分求解的走时计算程序(Podvin， Lecomte， 1991)计算出P波和S波的初至时刻， 将每个台站上接收的波形在S波开始的时刻分成P波与S波两个部分． 为了减小初至时刻不确定性的影响， 首先通过初至将波列初步对齐， 再通过波形互相关校正将模拟波形与观测波形对齐． 整个方法的处理流程可以概括如下：

1) 利用设定的速度模型计算格林函数库;

2) 使用有限差分走时计算程序计算P波和S波的走时， 根据走时信息将波形分成P波和S波两段;

3) 对于分开的P波和S波段： ① 通过模拟数据与观测数据的互相关确定时移， ② 计算对齐的模拟数据与观测数据的最大互相关值及二者之差的二范数， ③ 识别P波初动极性， ④ 分别计算P波段和S波段的平均振幅;

4) 通过求取目标函数最大值确定优化的震源机制解．

2 合成数据测试

为了验证全波形匹配方法的准确性和稳健性， 首先使用合成数据对其进行测试． 我们使用离散波数法生成理论地震图． 正演使用的台站和速度结构数据引自犹他州Cove Fort-Sulohurdale地热区实际监测台网和速度成像结果(张欣等， 2012)． 正演时将震源放置于地下3816 m处， 表征震源机制的3个参数分别为： 走向210°、 倾角50°、 滑动角20°． 合成的理论地震图在反演前需要手动进行P波初至的拾取和相应的极性判别． 反演过程中网格搜索时以震源所在位置为起始点， 水平方向的搜索范围为[-600 m， 600 m]， 间距为150 m． 由于地震记录对震源深度非常敏感， 震中深度上的较小变化都可能影响地震波多次反射、 折射的传播路径， 所以垂直方向上的搜索间隔设为100 m， 相应的搜索范围为[-400 m， 400 m]． 参数空间即走向、 倾角、 滑动角的搜索间隔均为10°．

图3给出了合成数据的震源机制反演结果． 我们选取了目标函数从大到小排列的前9个反演结果进行比较， 以表明反演结果的可靠性． 最优解(No.1)位于右下角， 震源机制参数为： 走向210°， 倾角50°， 滑动角20°， 与正演时的参数设置完全相同， 震源位置(0， 0， 0)也与正演时设定的地震位置完全吻合， 表明无论是震源机制还是空间位置均得到了很好的恢复．

图4给出了模拟数据与合成数据的波形匹配图． 每个子图中均给出了相应的“偏移”值， 表示将模拟数据与合成数据对齐所采取的时移(Δ)． 引入时移的原因有两个： 一是由于我们手动对波形数据进行P波初至的拾取， 不可避免地会引入一些误差； 二是地下散射体散射噪音也会对初至时间造成影响， 从而改变互相关最大值的位置(Noletetal， 2005)．

3 结果

3.1 地震震源机制

将上述方法应用于美国犹他州Cove Fort-Sulphurdale地热区所监测到的地震事件． 在台站布设的一年时间里， 台网共记录到了200多个地震事件(图2中红色圆点所示)． 从地表台站的记录来看， 这些地震的主要能量均集中在0.5—35 Hz． 图5给出了地面台站所记录到的一个典型事件的地震图及其相应的频谱图．

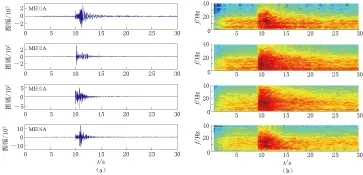
图5 一个典型事件的垂向记录(a)及其频谱(b)

图6 Cove Fort-Sulphurdale地区的一维层状P波和S波速度结构 Fig.6 1D layered velocity structure of P and S waves for Cove Fort-Sulphurdale

为了确定这些微小地震的震源机制， 需对研究区域的地下结构有一个比较清晰的了解． 张欣等(2012)利用双差走时层析成像(double-difference tomography, 简写为TomoDD)对Cove Fort-Sulphurdale地区记录到的200多个微震事件进行重新定位， 并对该地区进行成像， 得到了该地区的速度结构信息． TomoDD成像方法是利用相邻事件在同一台站上的到时差进行反演， 能够极大地减小绝对走时误差对反演结果的影响(Zhang， Thurber， 2003)． 利用反演得到的三维速度结构， 本文得到了Cove Fort-Sulphurdale地区的一维层状速度结构(图6)， 并使用该速度结构进行了格林函数库的计算和震源机制解的反演．

图7和8给出了Cove Fort-Sulphurdale地区4个具有不同震源机制的典型事件利用波形匹配震源机制确定方法得到的模拟数据与观测数据对比及相应的震源机制解． 可以看出， 实际数据与模拟数据的波形相似度非常高， 而且每个台站模拟数据与观测数据的P波初动极性也都非常相近， 说明两组数据的一致性非常高， 这也间接表明了本文结果的准确性． 需要注意的是， 尽管在某个台站波形匹配较好， 但其极性匹配却相反， 一个可能的原因是由于信噪比较差， 所拾取的波形极性信息不准． 另外， 对于大多数台站而言， 尽管其极性与波形匹配较好， 但其S/P波振幅比却有较大差异． 这可能是由于尽管在波形正演时考虑了地下介质衰减参数， 但所使用的一维衰减介质模型可能不能很好地表示真实的地下介质衰减情况所造成的． 因此传统的基于极性和振幅比确定震源机制的方法， 其结果可能具有较高的不确定性． 通过增加波形匹配的约束， 可以更可靠地确定震源机制． 图7和8也分别给出了4个典型事件相对应的最佳震源机制解． 可以看出， 其震中位置较初始位置分别沿东西(x)、 南北(y)向移动， 上下方向(z)也有偏移. 这可能是P波初至导致的定位误差， 也可能是由于所使用的一维层状速度结构不够精确所致． 如上所述， 震中位置的偏移可以补偿由于速度结构不精确而造成的模拟波形与实际记录的相位差异， 使反演结果更准确可靠．

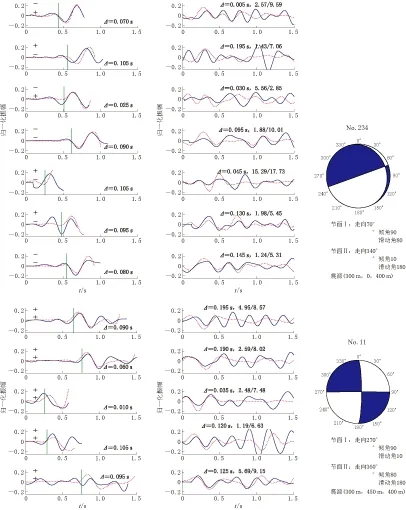
图8 No.234和No.11地震事件的震源机制解和波形匹配图． 图中说明同图4

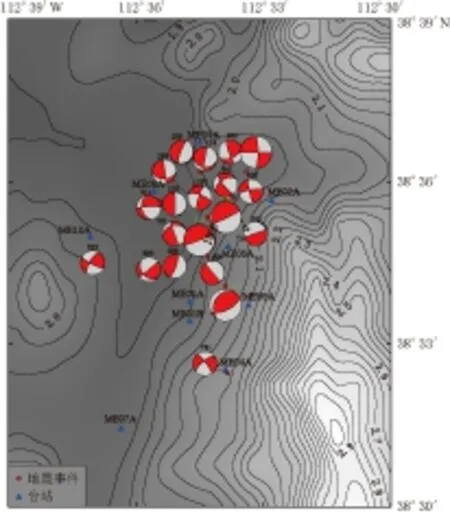
图9 20个地震事件的震源机制解 Fig.9 Distribution of focal mechanisms of 20 seismic events (red dots) determined by the waveform matching method

为了减小信噪比和台站方位角的影响， 确保反演结果的可靠性， 本文从200多个地震事件中挑选出信噪比较高、 台站覆盖较好的20个事件进行震源机制反演． 所选地震事件的位置及其相应的震源机制解结果如图9所示． 表1列出了这20个地震详细的震源机制解结果， 可以看到大多数发震断层为走滑断层(12个)， 也有少部分正断层(5个)和逆冲断层(3个)． 从图9和表1可以明显看出， 这些地震的断层面解的走向大部分趋于N--S向(13个)或NE向(5个)， 这意味着该地区的断层或裂缝的走向主要分布在N--S向上．

表1 20个地震事件的震源参数

3.2 基于震源机制解的应力分析

地震的震源机制解是认识地震发震断层及其破裂特征的主要方式， 同时， 震源机制解也反映了地壳内部的应力状况， 为构造应力场的研究提供了基础数据． 根据双力偶点源模型， 每次地震的震源机制解都给出了P轴、B轴、T轴的方位和两个节面参数， 其中一个节面是发震断层面． 由岩石力学实验结果可知， 通过断层面解求得的P轴和T轴只是反映了地震前后震源区应力状态的变化， 它们与构造应力的主轴方向之间存在一个偏角(钟继茂， 程万正， 2006)． 尽管如此， 由于P轴、B轴、T轴与主应力轴(S1，S2，S3)之间相差不会太大， 我们仍然能够使用P轴、B轴、T轴的方向来近似代表主应力的方向． 对于地理坐标系(o，x，y，z)， 其坐标原点o为震源，x轴指向北，y轴指向东，z轴垂直向下； 在双力偶点源模型条件下， 张应力轴方向矢量t、 压应力轴方向矢量p与断层面滑动矢量u和法向矢量v之间的关系为(Aki， Richards， 1980)

图10 Cove Fort-Sulphurdale地区20个地震事件的P轴(红色)和T轴(蓝色)分布轴线长短表示倾角大小， 线段越短表示倾角越大 Fig.10 Distribution of P (red) and T (blue) axes determined from focal mechanisms of 20 seismic events in the Cove Fort-Sulphurdale area The length of axis indicates inclination with the shorter line representing greater inclination angle

(3)

(4)

若断层面的走向φ、 倾角δ和滑动角λ均已知， 则滑动矢量u和断层面法向矢量ν可表示为

(5)

(6)

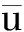
本文采用上述方法对Cove Fort-Sulphurdale地区发生的20个地震事件进行了主应力轴计算， 计算结果如图10所示． 可以看出， 中间部分的主压应力方向趋于N--S向， 两边趋于E--W和NNE向． Hickman和Zoback(2004)在美国加州中部SAFOD钻井也观测到相似的应力旋转现象. 这可能是由临近断层的滑动所引起的， 说明该地区存在地壳的活动变形， 仍处于构造活动区． 总的来说， 主压应力P轴的优势取向为N--S向和与其共轭的E--W向, 主张应力T轴的方位角相对离散， 主要集中在N--S和NNE两个优势方向． 统计显示P轴、T轴倾角大部分处于20°—40°之间(图11)， 表明该断裂带所承受的作用力以近水平向力和斜向力为主， 最大水平主应力优势取向与震源机制解参数结果比较一致．

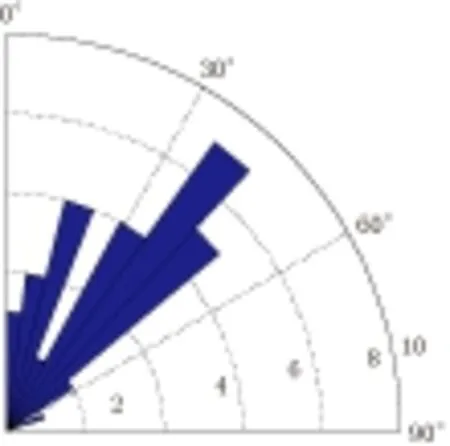
图11 P轴和T轴倾角统计图 Fig.11 Distribution of inclination angles for P and T axes

3.3 横波分裂分析

进行横波分裂研究的方法有很多种. 例如， 偏振分析法(Crampin， 1978)、 旋转分析法(Andoetal， 1983)、 自动分析法(Shihetal， 1989)、 偏振线性度定量估计法(Asteretal， 1990)、 自适应分析法(郑治真， 1990)、 最大特征值法(刘希强， 1992)、 相关函数分析法(高原， 郑斯华， 1994)、 偏振旋转法(李英康， 崔作舟， 1994)等． 本文主要使用快慢波波形互相关的方法(高原， 郑斯华， 1994)确定横波分裂参数．

图12给出了利用CDP(相关函数计算—时间延迟校正—偏振分析检验)方法对ME01A台站记录到的某次地震的波形进行横波分裂分析的流程． 可以看出， 横波极化方向和快慢横波之间的到时差经校正之后质点运动的线性特征与波形匹配得很好， 显示了该方法的可行性． 本文将上述横波分裂分析方法应用于Cove Fort-Sulphurdale地热区发生的200多个地震事件． 图13分别显示了所有地震事件的平均横波分裂延迟时间和快波极化方向． 其中图13a中的蓝色圆点表示在某个深度地震的慢波时间延迟， 我们选取了所有互相关系数大于0.7的地震事件， 并对某深度±0.5 km范围内所有地震事件所对应的时间延迟进行统计得出其平均值和标准差， 即图中所示的误差棒． 可以看出， 随着地震深度的增加， 慢波时间延迟并没有增大， 说明各向异性主要存在于浅部地区． 由图13b可以看出， 不同台站的平均极化方向也趋于一致， 均指向N--S向． 上述横波分裂分析结果表明， 如果各向异性主要是由该地区的断裂构造引起， 则该地区的主要断层或裂缝的方向应该是N--S向．

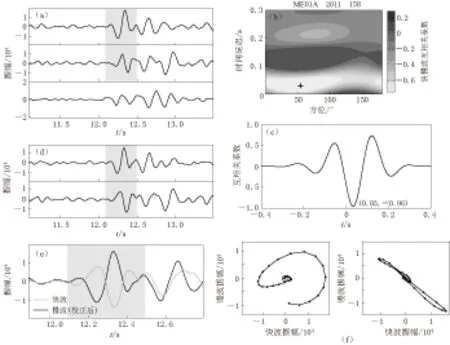
图12 CDP方法横波分裂分析流程图

图13 横波分裂分析的所有地震事件的平均时间延迟(a)和各台站快波极化方向(b)

4 讨论与结论

本文采用新的波形匹配算法进行震源机制反演， 与常规天然地震震源机制反演时所用频带(0.05—0.5 Hz)信息相比， 该方法能够利用地震仪记录到的高频波形信息(几Hz至几十Hz)， 在研究区域地下速度结构信息已知的情况下， 采用快速的网格搜索方法得到震源机制解和地震位置信息， 达到最佳波形匹配． 波形匹配目标函数中加入了P波初动和横纵波振幅比信息， 既充分利用了波形信息， 又可以对反演加以约束， 避免了仅靠波形数据反演导致的不确定性． 合成数据测试和实际应用均证实了该方法可以应用于地震等高频地震事件的精定位和震源参数计算， 反演结果稳定可靠．

Cove Fort-Sulphurdale地区20个地震事件的震源机制表明： 大多数地震发震断层为走滑断层， 也有少部分为正断层和逆冲断层； 其断层面的走向大部分趋于N--S向， 与该区域最大水平主应力优势取向N--S方向(Heidbachetal， 2009)具有较好的一致性． 由于该地区处于近E--W向的拉张应力作用下， 因此其主压应力方向应该是接近N--S方向． 本文所选取地震事件的震源机制和相应的应力分析结果均与该地区的区域地质构造特征比较一致， 符合目前人们对该地区的构造认知． 横波分裂分析结果也表明， 如果各向异性主要是由该地区的断裂构造所引起， 则该地区的主要断层或裂缝的方向应该是N--S向． 本文的各向异性研究结果显示快波的极化方向指向N--S向， 与震源机制分析所推断出的应力方向一致， 同时也与区域地质图上所显示的断层走向一致， 由此认为该研究区域的各向异性可能是由断裂构造和应力这两种机制共同引起的．

本文中震源机制反演采用的是双力偶点源模型和一维层状均匀速度结构， 这些与实际情况均存在一定的偏差． 若要得到精准的震源机制解和发震断层特征， 还需使用更精确的速度结构进行全矩张量反演， 以获得震源区完整的震源破裂特征． 同时可以考虑加入重力或电磁数据反演结果， 以便通过不同类型数据的约束， 更好地探讨Cove Fort-Sulphurdale 地热区的结构特征．

麻省理工学院李俊伦博士提供了震源机制反演程序， 麻省理工学院地球资源实验室提供了Cove Fort-Sulphurdale 地区的地震数据， 曾祥方博士提供了计算主应力轴的代码， 审稿专家对本文提出了宝贵意见和建议， 作者在此一并表示感谢.

高原， 郑斯华. 1994. 唐山地区剪切波分裂研究(Ⅱ)： 相关函数分析法[J]. 中国地震， 10(S)： 22--32.

Gao Y， Zheng S H. 1994. On shear wave splitting in Tangshan region (Ⅱ)： Correlation function analysis method[J].EarthquakeResearchinChina， 10(S): 22--32 (in Chinese).

李英康， 崔作舟. 1994. 分离纵波和横波的偏振旋转法[J]. 地球物理学报， 37(S2): 372--382.

Li Y K, Cui Z Z. 1994. P and S-wave separated by polarization revolving method[J].ChineseJournalofGeophysics, 37(S2): 372--382 (in Chinese).

刘希强. 1992. 剪切波分裂中的快、 慢波识别方法[J]. 西北地震学报， 14(4): 17--24.

Liu X Q. 1992. Methods to identify fast and slow S-wave in S-wave splitting[J].NorthwesternSeismologicalJournal， 14(4): 17--24 (in Chinese).

谢祖军， 郑勇， 倪四道， 熊熊， 王行舟， 张炳. 2012. 2011年1月19日安庆ML4.8地震的震源机制解和深度研究[J]. 地球物理学报， 55(5): 1624--1634.

Xie Z J， Zheng Y， Ni S D， Xiong X， Wang X Z， Zhang B. 2012. Focal mechanism and focal depth of the 19 January 2011 Anqing earthquake[J].ChineseJournalofGeophysics， 55(5): 1624--1634 (in Chinese).

许忠淮， 戈澍谟. 1984. 用滑动方向拟合法反演富蕴地震断裂带应力场[J]. 地震学报， 6(4): 395--404.

Xu Z H， Ge S M. 1984. Stress field in the Fuyun， Xinjiang earthquake fracture zone determined by fitting fault slip vector data[J].ActaSeismologicaSinica， 6(4): 395--404 (in Chinese).

张金华， 魏伟， 杜东， 魏兴华， 王培. 2013. 地热资源的开发利用及可持续发展[J]. 中外能源， 18(1)： 30--35.

Zhang J H， Wei W， Du D， Wei X H， Wang P. 2013. The development， utilization and sustainable development of geothermal resources[J].Sino-GlobalEnergy， 18(1): 30--35 (in Chinese).

张欣， 张海江， Toksöz M N. 2012. 美国Utah州Cove Fort-Sulphurdale地区三维衰减层析成像研究[C]∥中国地球物理学会第二十八届年会会议文集． 北京： 中国地球物理学会： 242.

Zhang X， Zhang H J， Toksöz M N. 2012. Three-dimensional seismic attenuation structure of the Cove Fort-Sulphurdale， Utah[C]∥ProceedingofChineseGeophysicalAnnualMeeting2012. Beijing: Chinese Geophysical Society: 242 (in Chinese).

郑克棪， 潘小平. 2009. 中国地热发电开发现状与前景[J]. 中外能源， 14(2)： 45--48.

Zheng K Y， Pan X P. 2009. Status and prospect of geothermal generation development in China[J].Sino-GlobalEnergy， 14(2): 45--48 (in Chinese).

郑勇， 马宏生， 吕坚， 倪四道， 李迎春， 韦生吉． 2009. 汶川地震强余震(MS≥5.6)的震源机制解及其与发震构造的关系[J]. 中国科学: D辑， 39(4): 413--426.

Zheng Y， Ma H S， Lü J， Ni S D， Li Y C， Wei S J. 2009. Source mechanism of strong aftershocks (MS≥5.6) of the 2008/05/12 Wenchuan earthquake and the implication for seismotectonics[J].ScienceinChina:SeriesD， 52(64): 739--753.

郑治真.1990. S波分裂的研究[J].地球物理学进展， 5(1): 8--13.

Zheng Z Z. 1990. Research of the shear wave splitting[J].ProgressinGeophysics， 5(1): 8--13 (in Chinese).

钟继茂， 程万正.2006. 由多个地震震源机制解求川滇地区平均应力场方向[J]. 地震学报， 28(4)： 337--346.

Zhong J M， Cheng W Z. 2006. Determinations of directions of the mean stress field in Sichuan-Yunnan region from a number of focal mechanism solutions[J].ActaSeismologicaSinica， 28(4): 337--346 (in Chinese).

Aki K， Richards P G. 1980.QuantitativeSeismology[M]. San Francisco: W H Freeman and Company: 115.

Ando M， Ishikawa Y， Yamazaki F. 1983. Shear wave polarization anisotropy in the upper mantle beneath Honshu， Japan[J].JGeophysRes， 88(B7): 5850--5863. doi:10.1029/JB088iB07p05850.

Aster R C， Shearer P M， Berger J. 1990. Quantitative measurements of shear wave polarization at the Anza Seismic Network， southern California: Implications for shear-wave splitting and earthquake prediction[J].JGeophysRes， 95(B8): 12449--12473.

Boness N L， Zoback M. 2004. Stress-induced seismic velocity anisotropy and physical properties in the SAFOD pilot hole in Parkfield， CA[J].GeophysResLett， 31(15): L15S17. doi:10.1029/2003GL019020.

Bott M H P. 1959. The mechanics of oblique slip faulting[J].GeologicalMagazine， 96(2): 109--117.

Bouchon M. 1981. A simple method to calculate Green’s functions for elastic layered media[J].BullSeismolSocAm， 71: 959--971.

Bouchon M. 2003. A review of the discrete wavenumber method[J].PureApplGeophys， 160(3/4): 445--465.

Crampin S. 1978. Seismic-wave propagation through a cracked solid: Polarization as a possible dilatancy diagnostic[J].GeophysJRastrSoc， 53(3): 467--496.

Crampin S. 1984. An introduction to wave propagation in anisotropic media[J].GeophysJInt， 76(1): 17--28.

Crampin S， Atkinson B K. 1985. Microcracks in the Earth’s crust[J].FirstBreak， 3(3): 16--20.

DeCelles P G， Coogan J C. 2006. Regional structure and kinematic history of the Sevier fold-and-thrust belt， central Utah[J].GSABulletin， 118(7/8): 841--864.

Gephart J W， Forsyth D W. 1984. An improved method for determining the regional stress tensor using earthquake focal mechanism data: Application to the San Fernand earthquake sequence[J].JGeophysRes， 89(B11): 9305--9320.

Heidbach O， Tingay M， Barth A， Reinecker J, Kurfeβ D, Müller B. 2009.TheWorldStressMapBasedontheDatabaseRelease2008,EquatorialScale1∶46000000[M]. Paris: Commission for the Geological Map of the World. doi:10.1594/GFZ.WSM.Map2009.

Hickman S， Zoback M. 2004. Stress orientations and magnitudes in the SAFOD pilot hole[J].GeophysResLett， 31(15): L15S12. doi:10.1029/2004GL020043.

Li J L， Zhang H J， Kuleli H S， Toksöz M N. 2011. Focal mechanism determination using high-frequency waveform matching and its application to small magnitude induced earthquakes[J].GeophysJInt， 184(3): 1261--1274.

Liu Y， Zhang H J, Thurber C, Roecker S. 2008. Shear wave anisotropy in the crust around the San Andreas fault near Parkfield: Spatial and temporal analysis[J].GeophysJInt， 172(3): 957--970.

Moore J N， Samberg S M. 1979.GeologyoftheCoveFort-SulphurdaleKGRA[R]. Utah: Univ Utah Res Inst， Earth Sci Lab， ESL-18: 44.

Nolet G， Dahlen F A， Montelli R. 2005. Traveltimes and amplitudes of seismic waves： A Reassessment[G]∥SeismicEarth:AnalysisofBroadbandSeismograms. AGU Monograph Series, 157: 37--48.

Podvin P， Lecomte I. 1991. Finite difference computation of traveltimes in very contrasted velocity models: A massively parallel approach and its associated tools[J].GeophysJInt， 105(1): 271--284.

Ross H P， Moore J N， Christensen O D. 1982.TheCoveFort-SulphurdaleKGRA:AGeologicandGeophysicalCaseStudy[R]. Utah: Univ Utah Res Inst， Earth Sci Lab， ESL-90: 47.

Ross H P， Moore J N. 1985. Geophysical investigations of the Cove Fort-Sulphurdale geothermal system， Utah[J].Geothermics， 50(11): 1732--1745.

Rutledge J T， Phillips W S. 2002. A comparison of microseismicity induced by gel-proppant-and water-injected hydraulic fractures， Carthage Cotton Valley gas field， East Texas[C]∥72ndAnnualInternationalMeeting,SEG,ExpandedAbstracts. Salt Lake: SEG: 2393--2396.

Shih X R， Meyer R P， Schneider J F. 1989. An automated， analytical method to determine shear-wave splitting[J].Tectonophysics， 165(1/2/3/4): 271--278.

Stein S， Wysession M. 2003.AnIntroductiontoSeismology，Earthquakes，andEarthStructure[M]. Malden， Massachusetts: Blackwell Publishing: 242--251.

Steven T A， Morris H T. 1983. Geologic map of the Cove Fort quadrangle， west-central， Utah[EB/OL]. [2014-08-09]. http:∥ngmdb.usgs.gov/Prodesc/proddesc_9256.htm.

Zhang H J， Thurber C. 2003. Double-difference tomography: The method and its application to the Hayward fault， California[J].BullSeismolSocAm， 93(5): 1875--1889.

Zhang H J， Liu Y F, Thurber C, Roecker S. 2007. Three-dimensional shear-wave splitting tomography in the Parkfield California region[J].GeophysResLett， 34(24): L24308. doi:10.1029/2007GL031951.

Zhu L P， Helmberger D V. 1996. Advancement in source estimation techniques using broadband regional seismograms[J].BullSeismolSocAm， 86(5): 1634--1641.

Focal mechanisms and seismic anisotropy analysis of local earthquakes at the Cove Fort-Sulphurdale geothermal site， United States

1)SchoolofEarthandSpaceSciences，UniversityofScienceandTechnologyofChina，

Cove Fort-Sulphurdale is located in central-western Utah， which is characterized by its unique geologic features and rich geothermal resources. For better development of geothermal reservoirs， it is necessary to have the know-ledge of stress and fracture distribution of the region. Based on the previous work， we use the waveform matching method to invert the focal mechanisms of local earthquakes collected in Cove Fort-Sulphurdale， constrained by first arrival P wave polarities and S/P amplitude ratios. Furthermore， we also use the shear wave splitting analysis method to study the anisotropy in this region. Combining both focal mechanism and anisotropy results， we can determine the stress distribution and fault/fracture directions. The results show that the waveforms of synthetic data match real data very well， and the first arrival P wave polarities and S/P amplitude ratios are close. Fault plane solutions have strikes trending in approximately N--S direction， which is consistent with the maximum horizontal principle stress indicated by the stress map of America and our current understanding of the tectonics in this region. Shear wave-splitting analysis results also show that if the anisotropy is mainly caused by the fault structure in this region， the strikes of the main faults/fractures should be in the N--S direction.

Cove Fort-Sulphurdale; focal mechanism; waveform matching; local earthquake; S/P amplitude ratio; geothermal; shear wave splitting; anisotropy

10.11939/jass.2015.06.002.

国家基金委项目(41274055)和“深部探测技术试验与集成”项目(SinoProbe-02)共同资助.

2015-02-04收到初稿， 2015-05-12决定采用修改稿.

e-mail: zhang11@ustc.edu.cn

10.11939/jass.2015.06.002

P315.01

A

张佩, 张海江, 刘影, 王华， Toksöz M N. 2015. 美国Cove Fort-Sulphurdale地热区地震震源机制和各向异性研究. 地震学报, 37(6): 899--915.

Zhang P, Zhang H J, Liu Y, Wang H, Toksöz M N. 2015. Focal mechanisms and seismic anisotropy analysis of local earthquakes at the Cove Fort-Sulphurdale geothermal site， United States.ActaSeismologicaSinica, 37(6): 899--915. doi:10.11939/jass.2015.06.002.