全要素生产率影响行业收入差距的实证研究

唐帅，王方方

(1.安徽财经大学统计与应用数学学院，安徽蚌埠 233030；2.兰州财经大学统计学院，甘肃兰州 730000)

全要素生产率影响行业收入差距的实证研究

唐帅1，王方方2

(1.安徽财经大学统计与应用数学学院，安徽蚌埠 233030；2.兰州财经大学统计学院，甘肃兰州 730000)

利用2003～2011年中国工业行业大类面板数据，运用MLD指数、非参数核密度估计和变系数模型从全要素生产率的角度考察了中国行业收入差距的影响因素。研究发现，中国工业行业的MLD指数呈下降趋势，但收入分布集中程度降低、尾部变厚；面板数据变系数模型结果表明全要素生产率是行业收入差距的重要影响因素，在不考虑其他因素的情况下对不同行业影响强度的差距在6.9%左右；随着其他影响因素的纳入，全要素生产率对单个行业影响程度在逐渐降低，其影响强度在行业间差距呈上升趋势。

全要素生产率；MLD指数；核密度估计；行业收入差距；工业行业

改革开放使中国的经济社会面貌发生了巨大变革，国内生产总值和城乡居民收入大幅度提高，各行业职工工资水平也普遍上升。但是，不同行业之间的工资差距正在拉大，这一现象受到了社会各界的普遍关注。一些学者担心中国行业收入分配会形成两极分化，损害社会公平，对行业发展、择业观念、社会风气造成不良影响。深入剖析中国行业收入差距形成的原因，有助于制定解决收入差距扩大问题的对策和措施，也有助于维护社会稳定、促进社会公平。因此，围绕行业收入差距扩大问题，很多学者做了大量研究。

影响收入差距的原因很多，学界对此已提出了一系列理论，如边际生产力理论、产业组织理论、人力资本理论和创新理论等，但这些理论大多考察了某一因素或某几个因素的影响。综观国内外有关文献，现有的研究大多从以下几个方面来考察行业收入差距的形成：第一，行业垄断因素，包括自然性垄断和行政性垄断两种表现形式。对中国而言，行政性垄断对行业工资水平的影响较大，这与中国现行所有制结构有关[1]。正是这种所有制结构使得不同企业间的劳动力市场出现分割，国有资本占主导地位的企业根据非市场因素制定工资，而非国有资本占主导地位的企业的工资水平是以市场为导向[2-3]。反映到行业中，不同行业国有企业的比重差异导致了巨大的行业间收入差距。从中国各行业每年平均劳动报酬数据，可以发现垄断行业收入显著高于非垄断行业。很多学者基于这种直观现象，考察了垄断行业和非垄断行业之间的收入差别。如杜鑫利用北京市人口抽样微观数据分析了中国城镇垄断性行业和竞争性行业之间的收入差距情况，发现垄断行业收入较竞争性行业约高50%[4]。武鹏在梳理、总结目前行业收入差距理论解释的基础上，分析了垄断对行业绝对收入差距的影响，结果表明过高的垄断行业收入水平导致中国行业收入差距上升了25%左右，其中不合理的差距占行业平均收入水平的1/4[5]。第二，人力资本因素。Sakellariou基于危地马拉和澳大利亚两地行业收入数据考察了收入差距的影响因素，证实了行业间工资收入差距确实受人力资本的外部性影响，但仍存在着不合理的收入差距，且不能为人力资本外部性所解释[6]。罗楚亮等根据2004年中国经济普查数据，从行业和企业两个角度考察了收入差距基本特征及其形成原因；研究发现，各受教育程度人群在行业就业人数中所占的比例对人均工资有显著影响，而在人均福利补贴的决定中，教育程度变量的影响不显著[7]。而邱兆林将垄断和人力资本及其交互项同时纳入了行业收入模型中，发现垄断和人力资本都会对行业收入差距产生影响，且二者之间存在交互效应，不同质量的人力资本在不同性质的行业中对收入差距的影响不同[8]。第三，劳动力需求因素。人力资本因素是从劳动供给方考虑的，而劳动力需求因素则是从需求方角度解释行业收入差距。Stigler认为寻找工作会带来信息成本，企业更倾向于根据岗位特征来制定工资标准，因此造成了行业间收入差距[9]。而Akerlof和Yellen认为某些行业会提高其工资水平以提高工人的劳动生产率，从而达到利润最大化的目标，由此导致了行业之间的工资差异[10]。而沿着这条路径发展出的效率工资理论在研究行业收入差距中广受关注。Krueger和Summers用效率工资理论解释了高工资行业的工人获得非竞争性的经济租的原因[11]。Thaler认为企业遵循“多得—多劳”的原则进行劳动投入的决策，这就使得支付比竞争性工资更多的劳动报酬会对企业利润的提高起到积极作用[12]。叶林祥等通过考察企业利润影响工资差距的途径，发现由效率工资导致的利润是企业工资差距形成的重要因素[13]。第四，技术进步因素。钟春平利用熊彼特“创造性毁灭”理论讨论了在新技术出现过程中的收入扩大趋势，研究发现能够适应新技术的个体会获得更高的收入[14]。孔庆洋等通过构建面板数据模型分析了工业行业技术进步及其分解指标对行业收入差距的影响，表明技术进步加剧了中国工业行业间的收入差距[15]。

在上述梳理行业收入差距影响因素的过程中，我们发现还存在着一些重要因素尚未得到学者的重视，如全要素生产率对行业收入差距的影响。全要素生产率是一个综合概念，其主要包含了4个方面的内容：技术进步、技术效率、规模效率和配置效率。一般认为，在全要素生产率上具有比较优势的企业或行业，其获得较高收入的可能性较大。除技术进步外，现有文献中人力资本和行业垄断因素也会对全要素生产率产业影响，如人力资本会对技术进步及技术效率产生影响，垄断因素则会影响规模效率和配置效率。但这都是从某个侧面研究了其影响效应，而从更宽、更综合的角度研究全要素生产率对行业收入差的影响在现有文献中是鲜见的。现有行业收入差距研究文献大多基于行业门类数据。但是由于行业门类的划分较为粗糙，不能很好地反映行业之间的差异，所以在很多情况下行业门类数据并不适合被采用。本文基于以上两点，首先采用工业行业大类数据对收入差距进行测度和分解；然后运用索洛余值法测算各行业的全要素生产率；最后将全要素生产率对行业平均报酬做回归分析，探讨其对于收入差距的影响。

一、模型、方法与数据

考虑到中国国民经济行业分类在2002和2011年发生过两次变动，为保持数据统计口径的一致性，本文研究样本时间跨度选择为2003～2011年。所有数据来源于历年《中国工业经济统计年鉴》、《中国劳动统计年鉴》以及2004、2008年经济普查数据。

(一)行业收入差距总体分析指标

在对中国工业细分行业收入差距总体状况进行分析时，本文主要采用两种方法：广义熵指数和核密度图法。Bourguignon指出广义熵指数中的对数偏差均值指数(Mean Log Deviation Index，简称MLD指数)是唯一可以用人口比重作为权数的相加可分解指标[16]，而核密度图则能刻画出行业收入的分布特征以及结构演进情况[17]。因此首先采用MLD指数对行业收入差距进行测度和分解，同时描绘出工业行业收入分布和演进情况的核密度图，从而对行业收入差距进行全面考察。

1.广义熵指数

广义熵指数是对收入份额度量的信息量族(GE Family)，是1967年泰尔在其利用信息论中平均信息量的概念所提出的泰尔指数基础上推广而来的。由于广义熵指数可以测度按某种标志分组后的子群间不平等，因此它能较准确地反映出总体的收入差距状况，其一般公式为：

(1)

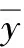
当α=0时，广义熵指数可以变形为MLD指数，该指数分配给低收入组的权重较大。因为MLD指数是以人口份额为权重的相加可分解指标，故采用该指数对工业细分行业收入差距进行测度和分解。MLD指数分解公式为[18]：

(2)

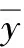
2.核密度图估计

通过对随机变量概率密度函数的估计，我们可以讨论其统计特征。非参数方法不要求事先对随机变量的分布做出假设，仅要求待估分布满足平滑性、可微性等条件，该方法越来越多地被研究者所采用。因此，本文采用非参数方法估计中国工业行业收入分布的概率密度函数，进而讨论其分布统计特征。非参数核密度估计是非参数密度估计方法之一，由Rosenblatt和Emanuel Parzen提出，又名Parzen窗[19-20]。其估计的表达式如下：

(3)

式中，Xi(i=1，2，…，n)和x分别表示一组随机样本和该组随机样本的均值,k(·)为所采用的核函数，hn表示光滑参数或窗宽，其定义与样本容量n有关，满足n→∞，hn→0。

由式(3)可以看出，一个核函数估计性质的好坏，主要取决于核函数k(·)和光滑参数hn的选取。一般在估计时对核函数施加诸如对成型、有界性、连续性等限制条件。而对于光滑参数hn的选取，最常见的方法有经验法、插入法、最小二乘交叉验证法以及似然交叉验证法。因经验法和插入法的主观性较强，似然交叉验证法较最小二乘交叉验证估计结果更加准确，本文将采用似然交叉验证法估计中国工业行业收入分布的概率密度函数。其基本思想是使如下对数似然函数最大化：

(4)

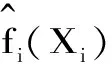
(二)全要素生产率对行业收入差距影响的计量分析

为验证全要素生产率(tfp)对行业收入差距的影响，首先要测算出各行业在2003～2011年期间的全要素生产率水平，然后在此基础上对其影响进行考察。

1.全要素生产率的测度

一般地，测度全要素生产率主要有参数方法和非参数方法两类。非参数方法主要有增长会计法和数据包络分析，其优点是不涉及参数的估计，但是它们只能反映全要素生产率的动态变化，不能对全要素生产率进行同一时刻不同截面上的横向比较。参数方法主要有经济计量法和随机边界分析，使用参数方法能综合考虑全要素生产率的各种影响因素，且能得到其水平值，但主要缺点是估计过程较为复杂。

因本文主要考虑不同时点不同截面上的全要素生产率水平值对行业收入差距的影响，故采用经济计量法测算中国工业细分行业的全要素生产率。首先，假定中国工业细分行业的生产函数形式为三要素投入的C-D生产函数：

(5)

式中，Ai0表示外生的技术进步；Yit，Lit，Kit和Mit分别表示第i个行业第t年的工业总产值、劳动投入、资本投入和中间投入；α、β和γ分别是劳动、资本和中间投入的产出弹性。将式(5)两边取自然对数，则有：

(6)

通过对式(6)回归，可得到劳动、资本和中间投入的产出弹性α、β和γ，正规化得到：

(7)

上述模型中的工业总产值以工业品出产价格指数按2003年不变价折算；资本投入参照李小平的做法，以固定资产年末净值表示[21]；中间投入采用式(8)推算；劳动投入以全部从业人员平均人数表示。

(8)

式中，mi(t)、gvi(t)、nvi(t)、depi(t)分别为第i行业以当年价表示的中间投入、总产值、净产值和折旧，pi(t)为第i行业的原材料、燃料、动力购进价格指数。

2.tfp对行业收入差距影响的面板数据模型

因面板数据能提供大量的数据点，增加数据的自由度，减小解释变量间的共线性程度，从而能提高计量模型估计的有效性[22]。借鉴武鹏在考察行业垄断对行业收入差距影响时对模型的设定方法[5]，本文采用如下3种形式面板数据模型估计全要素生产率(tfp)对平均行业劳动报酬的影响：

模型1：

lnincomeit=β0i+β1ilntfpit+εit

模型2：

lnincomeit=β0i+β1ilntfpit+β2ilnstaownit+β3ilnscaleit+β4ilnexportit+β5ilnsalesit+εit

模型3：

lnincomeit=β0i+β1ilntfpit+β2ilnstaownit+β3ilnscaleit+β4ilnexportit+β5ilnsalesit+β6ilnprofitit+β7ilncaplabit+εit

为了减少模型中存在的异方差，本文对所有变量均进行了对数化处理。上述3个模型中，income表示行业的平均劳动报酬，为被解释变量；全要素生产率tfp、国有资本占比staown、外向度export、产品销售率sales、人均利润profit、资本劳动比caplab和企业平均规模scale为被解释变量；εit表示随机误差项。在所有解释变量中，国有资本占比以国有资本占实收资本的比重表示，可以刻画由所有制结构而导致的行业行政性垄断程度；企业平均规模用行业资产总额与企业数之比表示，反映行业的自然性垄断程度；人均利润、资本劳动比分别定义为年度净利润、行业资产总额与行业从业人数的比率，用以描述

效率工资因素；其他控制因素为外向度和产品销售率，用出口产品销售额占总销售额的比重反映行业的外向度，产品销售率以销售产值在总产值比重表示。模型1为在不考虑其他因素情况下考察全要素生产率对行业平均劳动报酬的影响；模型2在模型1的基础上加入了垄断因素和其他控制变量；模型3在模型2的基础上进一步加入了劳动力需求方面的因素，包括效率工资因素。在建立全要素生产率与行业平均收入之间关系模型时，对所有以货币形式表示的指标均以2003年为基期的GDP折算指数进行平减。

二、实证结果及分析

(一)中国工业细分行业收入差距的总体分析

1.基于MLD指数对工业行业收入差距的测度和分解

根据中国2002年国民经济行业分类标准，工业行业分为3个大类、38个中类，大类包括采矿业，制造业电力、燃气及水的生产和供应业。我们根据前文所介绍的方法，采用对数均值偏差指数(MLD指数)按照行业大类对中国工业细分行业的收入差距进行测度和分解，具体结果如表1所示。

由表1可以看出，中国2003～2011年工业细分行业的收入差距呈波动下降趋势。其中，组内差距与总体收入差距基本保持着相同的变化趋势，而组间差距逐年上升。从组内差距与组间差距对总体收入差距的贡献度看，组内差距对总体差距的贡献度由2003年的85.7%下降到2011年61.7%；组间差距的贡献度由14.3%上升到38.3%，这表明中国工业行业大类间收入差距是减小的，而各门类间收入差距是逐年增大的。从行业门类角度分析可知，采矿业和电力、燃气及水的生产供应业的行业内收入差距是逐年降低的，而制造业的行业内收入差距呈上升趋势，但上升幅度较小。2003年采矿业的行业内收入差距最大，电力、燃气及水的生产供应业次之，制造业最小。而2011年三者之间的差距明显减小，3个大类行业的收入差距趋于一致。

2.行业收入分布的核密度估计

基于似然交叉验证法选取平滑参数的分布函数核密度估计方法，本文运用R软件中的非参数软件包估计了中国2003～2011年工业细分行业平均实际收入的分布函数。非参数核密度估计量和估计图分别见表2和图1。

表22003～2011年工业细分行业实际平均劳动报酬Kernel密度估计统计量

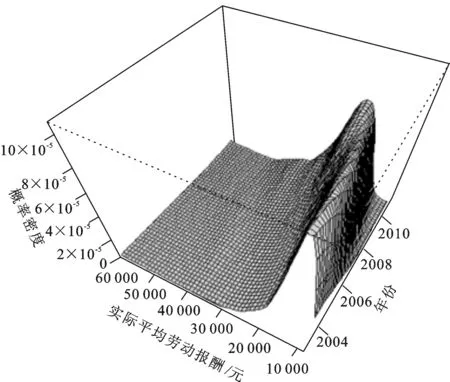
图1 2003～2011年工业细分行业收入分布结构演进

2003～2011年中国工业细分行业收入分布演进如图1所示，横轴分别表示实际平均劳动报酬和年份，纵轴表示概率密度。2003～2011年，工业细分行业的收入分布有如下几个特征：第一，行业平均劳动报酬集中点向左偏移，这表明中国行业收入在逐年增加；第二，三十多个工业行业的收入分布始终呈现单峰分布，这表明中国工业行业收入分布尚未出现两极分化格局；第三，收入分布的集中程度有所减小，具体表现为收入分布的峰度在逐渐降低、尾部在逐渐增厚，这表明了中国工业细分行业的收入差距存在拉大的可能。

(二)行业收入差距的计量分析

1.各行业全要素生产率的估计

在估计各工业行业的生产函数时，考虑到轻重工业可能具有不同的要素收入弹性，我们参考李小平的做法[21]，将所有工业行业分为轻工业和重工业*行业用符号表示：H1煤炭开采和洗选业、H2石油和天然气开采业、H3黑色金属矿采选业、H4有色金属矿采选业、H5非金属矿采选业、H6农副食品加工业、H7食品制造业、H8饮料制造业、H9烟草制品业、H10纺织业、H11纺织服装、鞋、帽制造业、H12皮革、毛皮、羽毛(绒)及其制品业、H13木材加工及木、竹、藤、棕、草制品业、H14家具制造业、H15造纸及纸制品业、H16印刷业和记录媒介的复制、H17文教体育用品制造业、H18石油加工、炼焦及核燃料加工业、H19化学原料及化学制品制造业、H20医药制造业、H21化学纤维制造业、H22橡胶制品业、H23塑料制品业、H24非金属矿物制品业、H25黑色金属冶炼及压延加工业、H26有色金属冶炼及压延加工业、H27金属制品业、H28通用设备制造业、H29专用设备制造业、H30交通运输设备制造业、H31电气机械及器材制造业、H32通信设备、计算机及其他电子设备制造业、H33仪器仪表及文化、办公用机械制造业、H34工艺品及其他制造业、H35废弃资源和废旧材料回收加工业、H36电力、热力的生产和供应业、H37燃气生产和供应业、H38水的生产和供应业。关于轻重行业的分类，主要参考朱钟棣的做法。轻工业包括：H6、H7、H8、H9、H10、H11、H12、H13、H14、H15、H16、H17、H20、H21、H34；其余为重工业。。根据Hausman检验结果，对轻重工业生产函数均采用了随机效应(RE)模型进行估计，具体估计结果如表3所示。

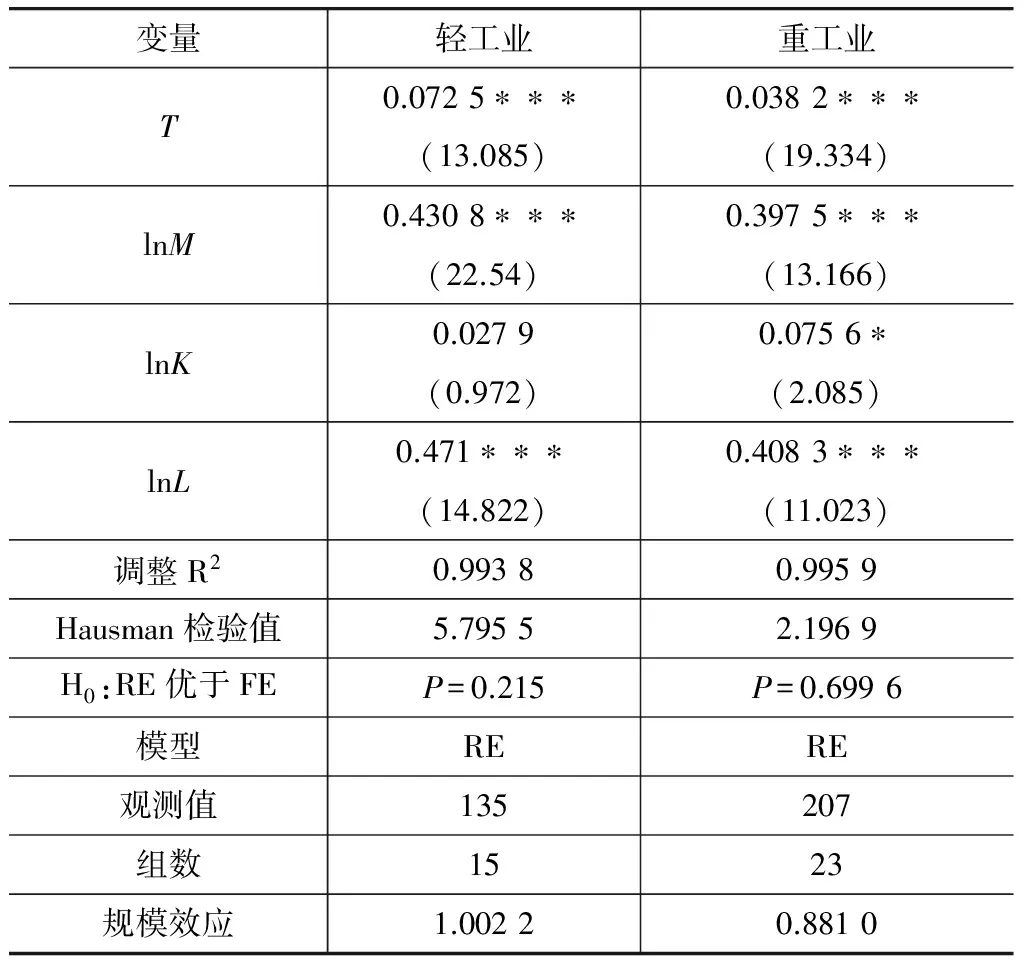
表3轻重工业生产函数估计结果

注：***、**和*分别代表在1%、5%和10%的显著性水平下显著；括号内为各估计量的t值。

从表3可知轻重工业回归方程的调整拟合优度(R2)均在90%以上，表明本文所估计的模型能很好解释行业的生产活动。从模型各参数的估计结果来看，劳动和中间投入的t值均在1%的显著性水平下显著，而资本投入的t值仅在重工业回归方程中达到10%显著水平。这主要是因为对于轻工业而言，资本的密集程度较低，短期内所投入的资金对生产经营活动的影响较小。从各变量系数的绝对值看，资本、劳动和中间投入弹性在轻重工业行业有较大差异。重工业部门的资本弹性大于轻工业，中间投入和劳动的弹性则小于轻工业，表明投入要素的弹性系数与要素使用的密集程度有关。将各要素投入弹性值相加，可以得到各工业部门的规模效应，轻工业部门的规模效应为1.002 2，重工业部门的规模效应为0.881 0。这说明重工业部门不存在规模效应，而轻工业部门具有一定的规模效应。将回归方程的估计结果带入式(7)中，我们可以计算出各行业各年的全要素生产率，中国工业行业2003～2011年全要生产率描述性统计量见表4所示。

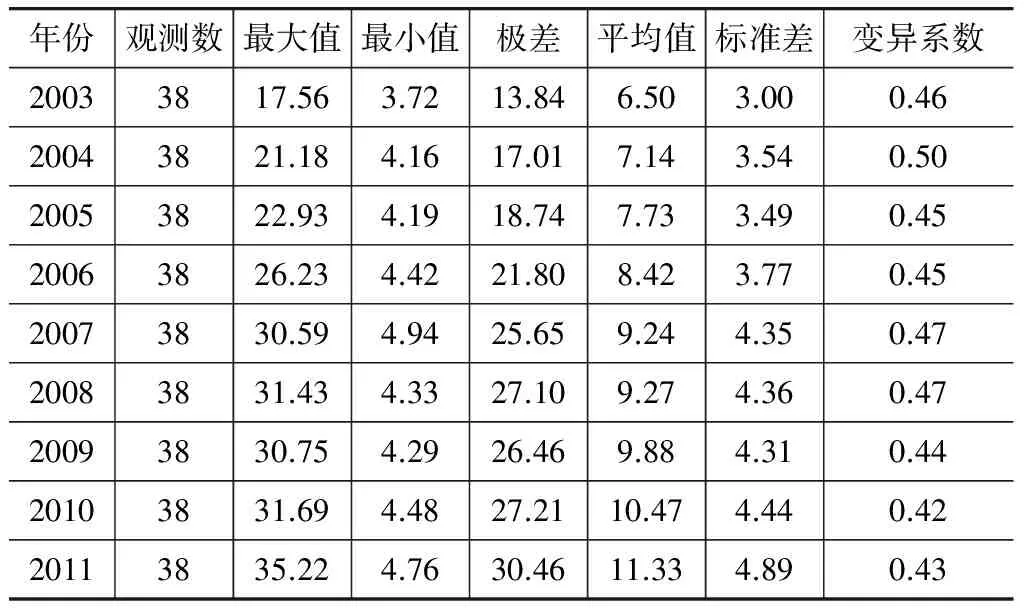
表42003～2011年工业行业全要素生产率描述性统计量

表4中中国工业行业各年全要素生产率均为正，说明了技术进步、技术效率、规模效率和配置效率在一定程度上对工业增加值做出了贡献，且全要素生产率平均值在2003～2011年间呈逐渐上升趋势，表明工业行业的各方面效率持续改进。但是，观察中国各年工业行业全要素生产率离散趋势指标，可以发现行业间全要素生产率差距呈逐渐拉大的趋势，极差、标准差分别由2003年的13.84和3.00上升到2011年的30.46和4.89，而变异系数指标表现平稳，始终处于0.42到0.50的区间之内。

2.行业平均劳动报酬的计量分析

在前文所构建的3种模型框架下，考虑全要素生产率(tfp)对平均劳动报酬的影响大小。为保证模型设置的合理性，应先对模型的设定进行检验，检验结果如表5所示。表5显示在原假设分别为变截距和混合模型下，3种模型设定检验结果均拒绝了原假设，表明我们应考虑建立变系数模型。然而本文主要考虑全要素生产率对于各截面的影响，因此采用固定系数变系数模型对其进行说明。

运用R软件中的plm包对变系数模型参数进行估计[23]。因结果较多，本文仅给出变量系数的估计值和t值，面板估计结果见表6～8。从整体上看，表6模型1回归方程拟合的判定系数为0.999 8，说明模型拟合程度较好。从各行业tfp系数估计的t值看，其系数在10%的显著性水平下均是显著的。由具体分析可知，在不考虑其他因素的情况下，虽然全要素生产率对各行业平均劳动报酬均产生了显著性影响，但是其影响方向和程度存在差异。从影响方向来看，全要素生产率(tfp)对H2(石油和天然气开采业)和H18(石油加工、炼焦及核燃料加工业)产生了负向影响，即随着这两个行业的tfp上升，其行业平均劳动报酬是下降的。根据匹配理论模型[24]，这可能是由于这两个行业的技术效率、技术进步、规模效率和配置效率均已达到较高水平，但是人力资本不能与之匹配，企业全要素生产率提高的成本并不能从效益中得到补偿，从而职工平均劳动报酬下降。而对于其他行业，全要素生产率均呈现正向影响。这表明，对于工业中的大部分细分行业，tfp的上升会促进平均劳动报酬的提高。从影响程度上看，正向影响行业中全要素生产率对H1(煤炭的开采和采选业)的影响最大，tfp每上升1%，职工平均劳动上升3.15%；对H32(通信设备、计算机及其他电子设备制造业)的影响最小，其弹性约为0.62。而在负向影响行业中，全要素生产率对H18的影响程度最大，弹性约为-3.76%。从各行业影响程度的差距看，极差和标准差分别为6.91和0.93，影响程度较大，这表明全要素生产率是影响行业收入差距的一个重要因素。

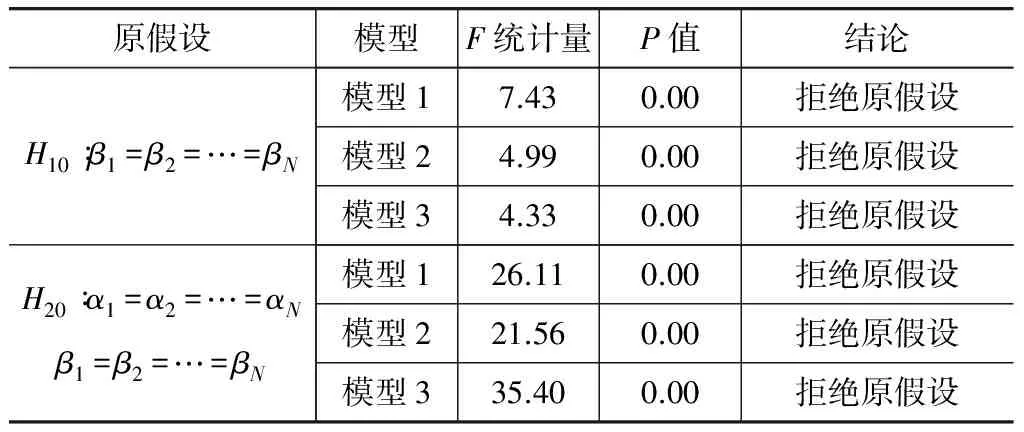
表5模型的设定检验统计量结果

表7模型2考虑了影响平均劳动报酬的行业垄断因素及其他控制变量，企业资本结构(国有资本比重)、企业平均规模、外向度和产品销售率等。因本文主要考虑全要素生产率对平均劳动报酬的影响，表7同样只给出了全要素生产率的系数值和t值。对比模型1和模型2全要素生产率系数估计结果，可以发现在纳入行业垄断因素及其他控制变量后，虽然行业平均劳动报酬的全要素生产率弹性在大部分行业出现了明显的下降，但系数仍是显著的。观察在模型2中β(tfp系数)值仍显著的行业，全要素生产率的弹性较模型1平均下降了约23.6%，表明在模型2中除全要素生产率之外还有其他因素对行业收入增长产生影响。还可以发现，部分行业的β值由模型1显著不为0下降为模型2中不能拒绝其等于0的原假设。这表明对于部分行业来说，在控制垄断因素后，全要素生产率对其行业收入水平的促进作用消失。因而，这个结果从另一方面反映了全要素生产率是影响行业收入差距的原因。

表6模型1全要素生产率系数估计结果

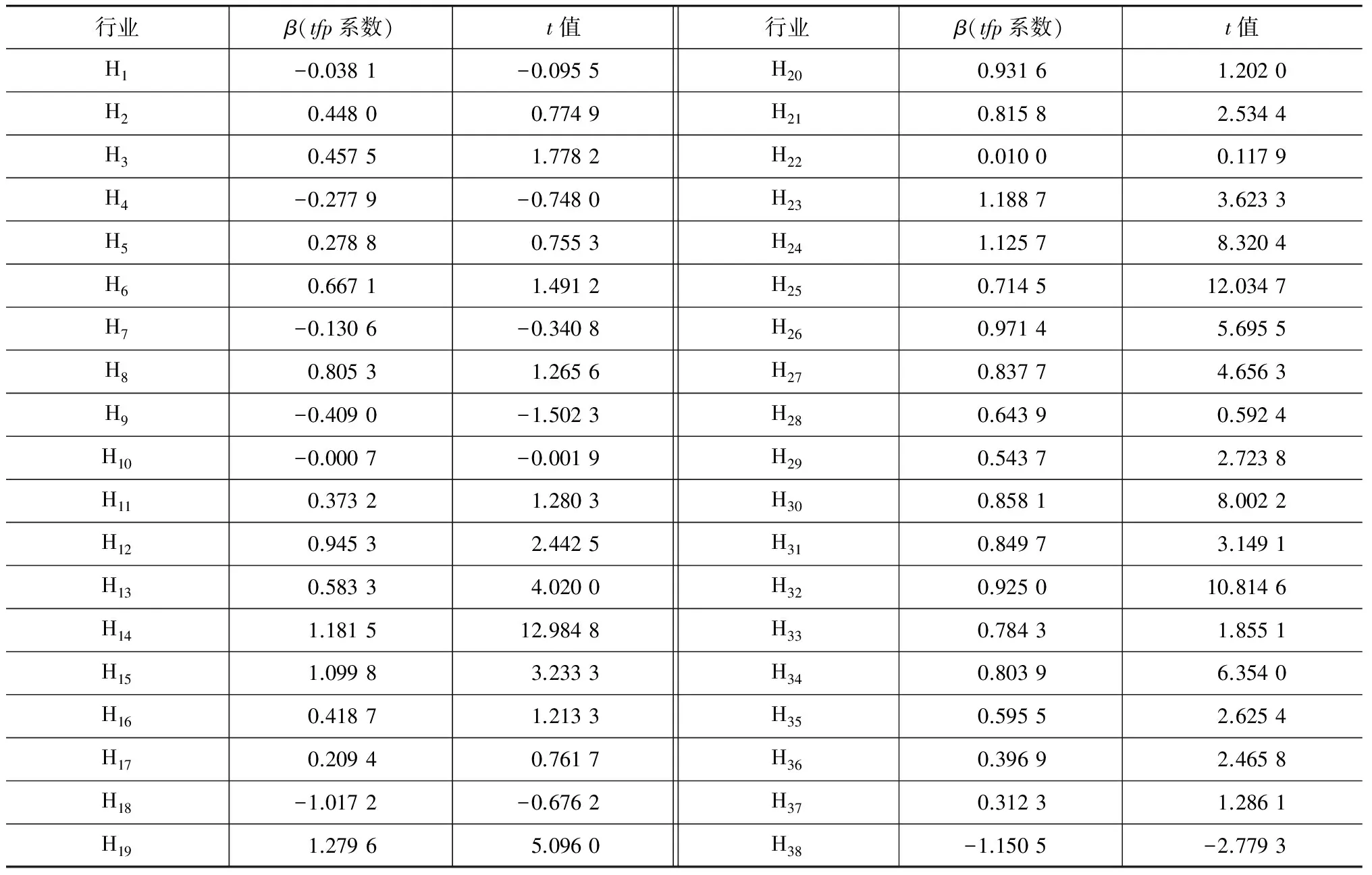
表7模型2全要素生产率系数估计结果

表8为在模型2基础上加入了效率工资因素的β(tfp系数)估计结果。对比模型2和模型3的估计结果，可以发现在控制人均利润、资本劳动比等因素后，各行业全要素生产率对平均劳动报酬的影响进一步降低，部分行业甚至由正向影响转变为负向影响。这表明效率工资等因素也是行业收入差别的重要影响因素。但是tfp对全部行业的影响并不是均为负向或者不显著，还存在部分行业受到正向影响，这意味着当这些行业全要素生产率的提高将拉大与其他行业平均劳动报酬的差距。具体来看，在控制效率工资后全要素生产率在各行业之间影响的最大差距约为8.8%，如H35的tfp弹性为2.482 6，而H16的弹性为-6.322 8。这表明了在控制垄断和效率工资方面的因素后，全要素生产率仍对行业劳动报酬产生了较大影响。

四、结语

本文对中国工业行业大类2003～2011年收入差距运用MLD指数进行了测度和分解，同时描绘了行业收入分布及其演进的核密度图，从总体上分析了工业行业收入发展现状。着重考察了全要素生产率对工业行业收入差距的影响，本文得出了如下结论：第一，从MLD指数和核密度图分析，中国2003～2011年间工业行业收入差距呈减小趋势，收入分布始终呈单峰形态；但其集中程度有所降低、尾部增厚，表明行业收入差距存在着向双峰转化的可能。第二，在不考虑其他影响因素的情况下，全要素生产率对所有行业的平均劳动报酬均呈显著影响，但影响方向和程度有所差异。其中，对两个石油行业(石油和天然气开采业以及石油加工、炼焦及核燃料

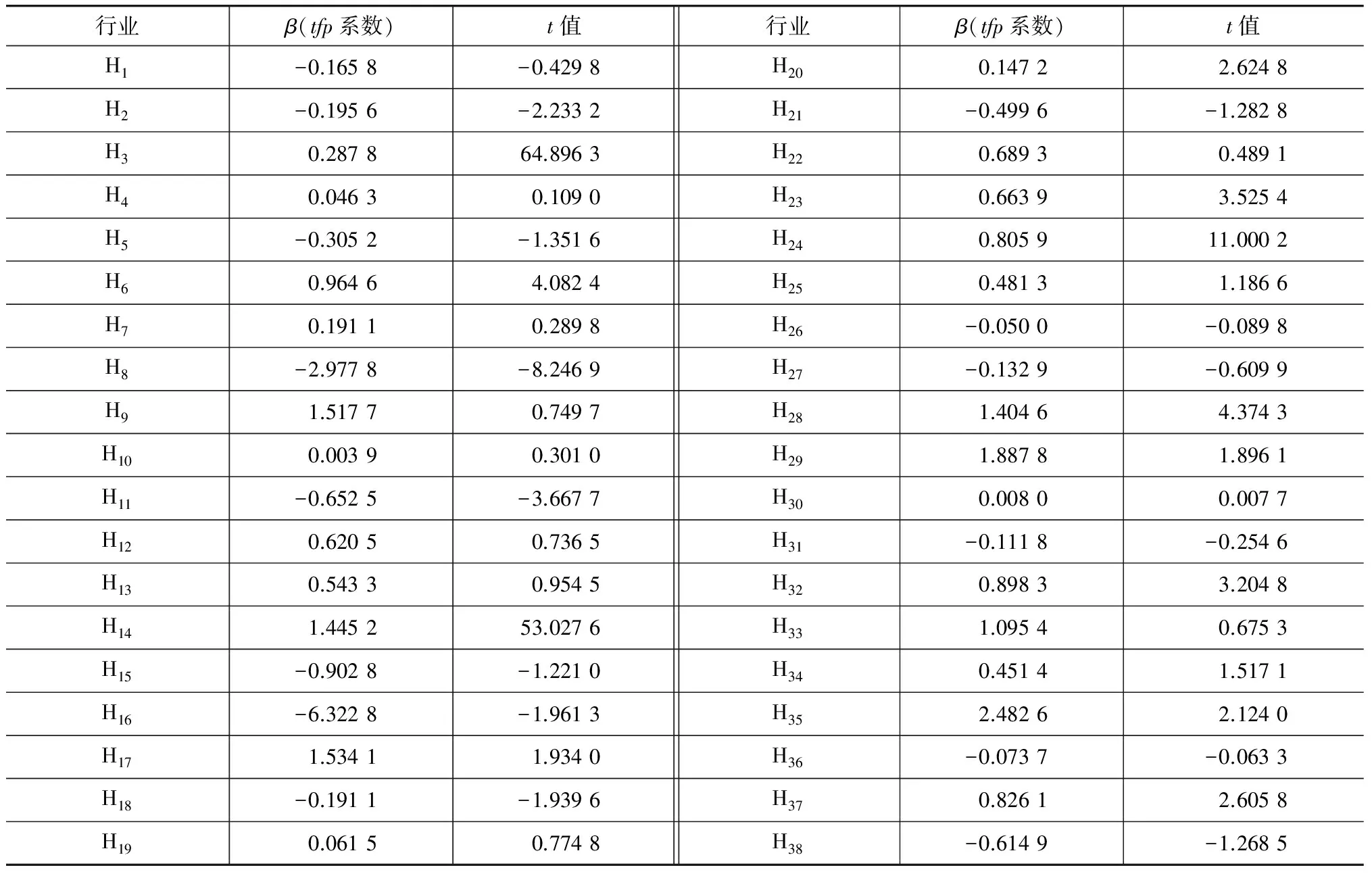
表8模型3全要素生产率系数估计结果

加工业)均产生了负向影响。在所有正向影响中，全要素生产率在各行业之间影响的最大差异为6.91%。第三，在加入行业特征因素及垄断因素后，全要素生产对行业平均劳动报酬的影响程度减小，但是对大部分行业还是存在显著影响的；但其影响程度较不控制其他因素情况平均下降了25%左右。第四，在加入效率工资影响因素的情况下，各行业全要素生产率对平均劳动报酬的影响程度进一步降低，部分行业甚至由正向影响转变为负向影响；但是，全要素生产率在各行业间影响的最大差距由不控制任何因素情况下的6.91%上升到8.8%。以上结论可以充分表明全要素生产率是影响行业收入差距的一个重要因素。

为了尽量减少行业间的收入差距，在以上研究结论的基础上，笔者提出以下政策建议：第一，各行业之间的全要素生产率存在差别，应加大基础行业的物质资本和人力资本的投资，提高各行业的全要素生产率，缩小行业间全要素生产率的差距；第二，行业垄断的存在使得行业间收入差距进一步扩大，应采取措施打破行业垄断，解决垄断企业内部工资管理体制和收入分配制度的不合理，从根本上解决垄断行业职工收入过高的问题；第三，减少行业间效率工资的差异，而效率工资的提高依赖于企业的经营。因此，企业应优化经营模式，努力降低经营成本，提高超额利润。

[1] 金玉国.我国行业工资水平与垄断程度关系的定量测度[J].江苏统计,2001(3):30-31.

[2] 邢春冰.不同所有制企业的工资决定机制考察[J].经济研究,2005(6):16-26.

[3] Demurger S, Fournier M, Shi L, et al. Economic liberalization with rising segmentation in China’s urban labor market[J].Asian Economic Papers,2006,5(3):58-101.

[4] 杜鑫.中国垄断性行业与竞争性行业的收入差距:基于北京市微观数据的研究[J].南开经济研究,2011(5):111-124.

[5] 武鹏. 行业垄断对中国行业收入差距的影响[J].中国工业经济,2011(10): 76-86.

[6] Sakellariou C.Human capital and industry wage structure in Guatemala[R]. Washing ton: The World Bank Policy Research Working Paper,1995.

[7] 罗楚亮,李实.人力资本、行业特征与收入差距——基于第一次全国经济普查资料的经验研究[J].管理世界,2007(10):19-30.

[8] 邱兆林.行业垄断、异质性人力资本与行业收入差距[J].经济与管理评论,2014(5):18-25.

[9] Stigler G J. Information in the labor market[J].The Journal of Political Economy,1962,70(5):94-105.

[10] Akerlof G A, Yellen J L. The fair wage-effort hypothesis and unemployment[J].The Quarterly Journal of Economics,1990,105(2):255-283.

[11] Krueger A B, Summers L H. Efficiency wages and the inter-industry wage structure[J].Econometrica: Journal of the Econometric Society,1988,56(2):259-293.

[12] Thaler R H. Anomalies: inter-industry wage differentials[J].The Journal of Economic Perspectives,1989,3(2):181-193.

[13] 叶林祥,李实,罗楚亮.效率工资、租金分享与企业工资收入差距——基于第一次全国经济普查工业企业数据的实证研究[J].财经研究,2011,37(3):4-16.

[14] 钟春平.创造性破坏与收入差距的振荡扩大：基于中国行业工资的经验分析[J].上海经济研究,2004(2):3-10.

[15] 孔庆洋,黄济生.行业垄断、技术进步与行业收入差距——基于工业二位数行业的分析[J].华东师范大学学报：哲学社会科学版,2012(2):102-110.

[16] Bourguignon F.Decomposable income inequality measures[J].Econometrica: Journal of the Econometric Society, 1979,47(4):901-920.

[17] 顾严,冯银虎. 我国行业收入分配发生两极分化了吗？——来自非参数Kernel密度估计的证据[J].经济评论,2008(4):5-13.

[18] 王倩,姜琪.资本深化下的行业收入差距分析[J].财经科学,2013(5):95-104.

[19] Rosenblatt M.Estimation of the cross spectra of stationary vector processes[J].New York University Engineering Statistics Group,1955,285:17.

[20] Parzen E.On estimation of a probability density function and mode[J].The annals of mathematical statistics, 1962：1065-1076.

[21] 李小平,朱钟棣. 中国工业行业的全要素生产率测算——基于分行业面板数据的研究[J].管理世界,2005(4):56-64.

[22] 高铁梅.计量经济分析方法与建模:EViews应用及实例[M].北京:清华大学出版社,2009.

[23] Croissant Y, Millo G. Panel data econometrics in R: The plm package[J].Journal of Statistical Software,2008,27(2):1-43.

[24] Kremer M, Mskin E. Wage inequality and segregation by skill[R].Washing ton：NBER Working Paper,1996.

Empirical study on the influence of total facto productivity on industry income gap

TANG Shuai1, WANG Fang-fang2

(1.School of Statistics and Applied Mathematics，Anhui University of Finance and Economics， Bengbu 233030, Anhui, China；2.School of Statistics，Lanzhou University of Finance and Economics，Lanzhou 730000, Gansu, China)

Using the industry high group panel data of China from 2003 to 2011, this paper examined the influence factors of total factor productivity on industry income gap based on the MLD index, nonparametric kernel density estimation and varying coefficient model. The results show that the total factor productivity is indeed an important factor of industry income gap. Specifically, the MLD index of China’s industrial sector shows a downward trend, the degree of income distribution concentration is decreasing, and the tail is getting thicker. In addition, the result of varying coefficient models shows that without considering other factors the strength of the gap between industries is around 6.9%. With the inclusion of other factors, the influence of total factor productivity on each independent industry is gradually decreasing. However, the impact strength of the gap between industries is rising.

total factor productivity; MLD index; kernel density estimation; industrial income gap; industry

2014-12-05

唐帅(1991-)，男，安徽池州人，经济学硕士研究生。

F047

A

1671-6248(2015)03-0042-10