地下铲运机自主行驶与避障控制方法研究

石 峰，顾洪枢，战 凯，李建国，冯孝华，郭 鑫，李恒通，陈 维，石金鹏

（1.北京矿冶研究总院，北京100160；2.德纳管理（上海）有限公司，上海200443；3.鞍钢集团公司，辽宁鞍山114007）

地下铲运机自主行驶与避障控制方法研究

石 峰1，顾洪枢1，战 凯1，李建国1，冯孝华1，郭 鑫1，李恒通1，陈 维2，石金鹏3

（1.北京矿冶研究总院，北京100160；2.德纳管理（上海）有限公司，上海200443；3.鞍钢集团公司，辽宁鞍山114007）

由测量数据或轨迹推算模型，计算铲运机横向位置偏差、航向角偏差及航向角偏差变化率，三偏差通过非线性融合规则，形成融合偏差反馈信号并作为PID校正控制的输入量，设置横向位置偏差及航向角偏差双门限值来改进PID算法。该自主行驶控制方法在轨迹偏差及行驶车速大范围变化时，仍能保持优良的稳定性和快速性。

地下铲运机；自主行驶；避障；控制算法

随着地下矿开采深度的增加，采矿条件越来越恶劣，对人的安全威胁也越来越大，遥控采矿、自动化矿山开采技术应运而生［1－3］。地下铲运机是地下无轨采矿的关键设备，可以实现地下铲运机在井下巷道内无人操纵、自主行驶，使操作工人远离井下恶劣、危险的工作环境，保护铲运机司机人身安全，提高采矿作业效率，降低采矿成本。

由于井下巷道断面不规则，巷道壁凹凸不平，使得沿墙行走导航方式受到一定程度的限制。另外，井下巷道内经常会沿巷道壁放置通风机、电气开关柜等设施，形成局部障碍，使得地下铲运机并不总是等距离地沿墙行走，避障运动控制是地下自主铲运机一项必不可少的功能。因此，在地下巷道环境下，有必要事先规划出目标路径，并采用相对定位与绝对定位相结合的方法，来确定铲运机相对于目标路径的偏差，通过自主避障行驶控制器的控制作用，使地下铲运机自主跟踪目标路径并实现避障［4］。

1 地下铲运机目标路径及跟踪轨迹参数关系

巷道内的地下铲运机主目标路径、局部避障目标路径、跟踪轨迹及相关参数说明示意图见图1。

以巷道路面为坐标平面建立x－y坐标系，选取铲运机前方驱动桥的中点为铲运机的定位参考点，以该点在x－y坐标平面上的投影点P代表铲运机的位置。以P点的速度方向（轨迹切线方向）作为车辆的运动方向，其与x轴正方向所成的夹角定义为铲运机的航向角φg，取从x轴逆时针旋转形成的航向角为正，反之为负。P点的运动轨迹即为铲运机的跟踪轨迹，见图中曲线C。在巷道内预先规划好的P点运动目标路径作为铲运机的主目标路径，见图中曲线A。为了避障，在巷道内局部区域规划出与主目标路径横向等距偏移的P点运动目标路径为局部避障目标路径，见图中曲线B，其中，横向偏离位移用δb0表示，取局部避障目标路径在主目标路径曲线左侧的横向偏离位移为正，反之为负。P点在目标路径上的垂直投影点Pm的速度方向与x轴正方向所成的夹角，定义为目标路径的航向角φm。由于局部避障目标路径上每一点是等距且平行于主目标路径上的对应点，所以P点在主目标路径上的垂直投影点Pm的速度方向与P点在局部避障目标路径上的垂直投影点Pmb的速度方向是相同的，即主目标路径和局部避障目标路径的航向角均为φm。主目标路径或局部避障目标路径的航向角φm与铲运机跟踪轨迹航向角φg的差值，定义为航向角偏差β，β＝φm－φg，该参数反映了自主铲运机运动方向与目标路径预定的行驶方向的偏差。铲运机跟踪轨迹上P点与主目标路径上Pm点的距离定义为铲运机的横向位置偏差δ。取P点在目标路径曲线右侧的横向位置偏差为正，反之为负，该参数可反映出铲运机相对于主目标路径的横向定位情况。铲运机跟踪轨迹上P点与局部避障目标路径上Pmb点的距离定义为铲运机的横向位置偏差δb。取P点在局部避障目标路径曲线右侧的横向位置偏差为正，反之为负。该参数可反映出铲运机相对于局部避障目标路径的横向定位情况，并且有δb＝δ＋δb0。为了计算方便，地下铲运机定位P点位置坐标由对应的主目标路径Pm点的曲线弧长sm和铲运机横向位置偏差δ来表示，即P（sm，δ）。Kg为跟踪轨迹在P点的曲率，当曲率中心Og在车辆轨迹曲线前进方向的左侧时定义为正曲率，曲率半径Rg为正，反之为负。Km为主目标路径在Pm点的曲率，Rm为其曲率半径，Om为曲率中心。Kmb为局部避障目标路径在Pmb点的曲率。铲运机P点行驶车速vg与轨迹曲线C相切，在实际自主行驶控制过程中，车速vg由安装在车辆底盘传动系统的车速传感器或里程计测量得到。主目标路径上Pm点投影车速为vm，投影车速vm与主目标路径曲线A相切，局部避障目标路径上Pmb点投影车速为vmb，投影车速vmb与局部避障目标路径曲线B相切。取铲运机运动方向为主目标路径曲线弧长sm的正方向，铲运机沿局部目标路径运动的曲线弧长为smb。α为铲运机转向角，即铲运机前后车体的相对转动角，由安装在铲运机前后车体铰接处的转角传感器测量得到。使地下铲运机反时针转弯的转向角α为正，反之为负。l1为铲运机前方驱动桥的中点到铰接中心线的距离，l2为铲运机后方驱动桥的中点到铰接中心线的距离。

图1 目标路径、跟踪轨迹及参数定义Fig.1 Target path，tracking trajectory and the definition of parameters

经过公式推导，可得出以下反映地下铲运机目标路径及跟踪轨迹参数关系的方程组：

2 三偏差融合自主行驶控制特性分析

2.1 三偏差融合反馈控制

将地下铲运机自主行驶控制器设计成三偏差融合反馈结合PID校正的行驶控制器，其中三偏差融合反馈e的计算公式见式（2）［5］。

式中：δb—包括避障工况的横向位置偏差，β—航向角偏差为航向角偏差变化率；K1、K2和K3分别为横向位置偏差、航向角偏差和航向角偏差变化率的反馈系数，K1、K2和K3的选取范围均为0～1，且K1＋K2＋K3＝1。较佳的K1、K2和K3系数值分别为0.2≤K1≤0.3、0.3≤K2≤0.6、0.2≤K3≤0.4。

三偏差信息融合反馈形成三种控制作用的相互制约，避免了单一反馈控制的局限性，使得自主行驶控制具有预测性和前瞻性，通过改变K1、K2和K3的相对大小，可以改变三项偏差在反馈中的权重，方便地调节自主行驶控制系统总的响应特性。除了横向位置偏差δb、航向角偏差β，由公式可知，航向角偏差变化率包含有车速vg、目标路径曲率Km和转向角α，可以将车速vg、目标路径曲率Km和转向角α的影响适当反映进来，所以该三偏差信息融合自主行驶控制具有较好的控制性能。

2.2 横向位置偏差限幅控制

对于自主行驶控制系统，在较小的横向位置偏差δb（如δb＜1m）时，即横向位置偏差δb在小范围变化时，控制的快速稳定均衡关系比较容易实现。但是，当有较大的横向位置偏差δb（如δb＞1m）存在时，由上式计算出的三偏差融合反馈e的数值较大，这时横向位置偏差δb的作用效果过强，而航向角偏差β和航向角偏差变化率的作用相对较弱，导致自主行驶控制系统超调加大、振荡加剧，破坏了三偏差之间的均衡作用，甚至使控制系统失去稳定。另外，如果以此时较大的横向位置偏差δb来调整自主行驶控制系统参数K1、K2和K3，使其有较好的控制效果，那么当存在较小的横向位置偏差δb时，自主行驶控制系统的响应就会较慢，控制效果也会变差。即当横向位置偏差δb在较大范围变化时，自主行驶控制系统要么失去快速性，要么失去稳定性，两者很难兼顾。

因此，为了使导航控制效果在横向位置偏差δb较大范围变化时，仍有较好的控制效果，对横向位置偏差δb进行限幅控制，限幅值εδ1的取值范围是0＜εδ1≤1（m）。当－εδ1≤δb（k）≤εδ1时，δb（k）＝δb（k）。当δb（k）＞εδ1时，δb（k）＝εδ1。当δb（k）＜－εδ1时，δb（k）＝－εδ1。通过调整限幅值εδ1的大小来慢速释放较大横向位置偏差δb对导航控制器的过大作用量，保持导航控制系统三偏差之间的均衡作用，实现导航控制系统的快速性与稳定性的统一，该方法简单可靠、调整方便，对横向位置偏差δb较佳的限幅范围是0.4≤εδ1≤0.8（m）。

横向位置偏差有限幅与无限幅时的跟踪曲线比较见图2。此时，横向位置偏差反馈系数K1＝0.2，航向角偏差反馈系数K2＝0.55，航向角变化率偏差反馈系数K3＝0.25，横向位置偏差δb限幅值εδ1＝0.6m，横向偏差初始值δ0＝1m，δ0＝3 m，δ0＝5m，航向角偏差初始值β0＝0°，转向角初始值α0＝0°，车速vg＝8km/h。当横向位置偏差无限幅作用时，当δb＞1m时，响应超调加剧，甚至失去稳定性；当横向位置偏差有限幅作用时，导航控制系统稳定性保持良好，无超调和失稳，跟踪效果明显优于横向位置偏差无限幅作用情况。

2.3 双门限改进型PID控制

PID校正控制是工程上最常用的控制方案，PID控制器是最简单但许多时候仍是最好的控制器［6－7］。但是，常规的PID校正控制也存在不足之处，如比例控制不能消除稳态误差，积分作用太强会使系统超调加大，而积分作用太弱又会使系统消除稳态误差的作用时间延长，降低系统控制精度。

对PID校正控制进行改进设计，分别设置横向位置偏差δb门限值εδ2和航向角偏差β门限值εβ，用来检测铲运机跟踪轨迹是否已经接近目标路径。当铲运机跟踪轨迹的横向位置偏差δb的绝对值大于门限值εδ2时，说明此时铲运机跟踪轨迹的横向位置偏差还较大，这时还不必考虑消除稳态跟踪误差，故不必应用积分控制，控制系统仅需要根据三偏差融合反馈e的情况结合PD校正进行控制，从而避免了积分饱和现象，避免了产生过大的超调。当铲运机跟踪轨迹的横向位置偏差δb的绝对值小于门限值εδ2时，这时由于横向位置偏差δb的数值较小，产生的控制作用比较弱，加上系统死区的存在，会使控制系统消除横向位置偏差δb的能力减弱，调整时间延长，并产生较大稳态误差。为了避免这种情况，此时加入积分控制作用，通过积累较小控制作用形成较大控制作用，加大了系统消除较小误差的能力，减小调整时间，消除存在的稳态误差。考虑到在铲运机横向位置偏差δb较小的同时，可能存在航向角偏差β数值较大的情况，如果这时加入积分作用，会使系统超调加大，振荡加剧。所以，在设置横向位置偏差δb门限值εδ2的同时，设置航向角偏差β门限值εβ。仅当双门限要求同时满足时，即且才进行融合偏差反馈信号e的PID控制，否则仅进行PD控制，以保证系统的控制效果，这样可避免产生过大的超调，又使系统有较快的响应和较小的稳态误差。其中，εδ2的取值范围为0＜εδ2≤0.3（m），较佳的门限值εδ2的取值范围是0.1＜εδ2≤0.2（m）；εβ的取值范围为0＜εβ≤0.3（rad），较佳的门限值εβ的取值范围是0.03＜εβ≤0.2（rad）。

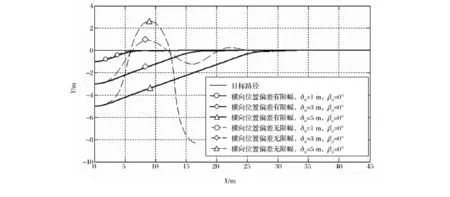
图2 横向位置偏差有限幅与无限幅时的跟踪曲线比较图Fig.2 Tracking curves comparison between lateral position deviation amplitude limited and not limited

通过横向位置偏差及航向角偏差双门限控制，融合偏差反馈信号e获得较理想PID校正控制效果。双门限积分控制与常规积分控制跟踪曲线比较见图3，此时横向位置偏差反馈系数K1＝0.2，航向角偏差反馈系数K2＝0.55，航向角变化率偏差反馈系数K3＝0.25，横向位置偏差δb的限幅值εδ1＝0.6m，PID的比例系数Kp＝30，PID的微分系数Kd＝0，PID的双门限时积分系数Ki＝18，常规积分时积分系数Ki＝3，横向位置偏差δb门限值εδ2＝0.150m，航向角偏差β门限值εβ＝0.06rad，横向偏差初始值为δ0＝0m，航向角偏差初始值分别为β0＝－20°，β0＝－40°，β0＝－60°，转向角初始值α0＝0°，车速vg＝8km/h，从图3可以看出双门限积分控制时的跟踪效果明显优于常规积分控制时的跟踪效果。

图3 双门限积分控制与常规积分控制跟踪曲线比较图Fig.3 Tracking curve comparison between double threshold integral control and conventional integral control

3 地下铲运机自主避障行驶控制算法

将横向位置偏差δb经过限幅εδ1后再与航向角偏差β、航向角变化率偏差三种偏差进行融合，形成融合偏差反馈e信号作为PID控制的输入，在PID校正控制中，分别设置横向位置偏差δb门限值εδ2及航向角偏差β门限值εβ，仅当双门限εδ2和εβ要求同时满足时才进行融合偏差反馈信号积分，PID校正后的输出信号作为车辆转向控制指令u，输入给铲运机的电液比例转向控制系统，驱动车辆转向并跟踪目标路径，实现地下铲运机自主行驶运动控制。

地下铲运机自主行驶控制算法框图见图4。

图4 地下铲运机自主行驶控制算法框图Fig.4 Underground loader autonomous driving control algorithm flow chart

该地下铲运机自主避障行驶控制算法主要步骤如下：

1）在地下自主铲运机主目标路径和局部避障目标路径规划完成后，沿主目标路径曲线弧长sm（k）（k＝1，2，3，…）存储主目标路径曲率Km（k）系列值，沿主目标路径曲线弧长sm（k）存储局部避障目标路径的起始点smbb（i）和终止点smbe（i）（i为局部避障目标路径数量，i＝1，2，3，…），存储局部避障目标路径相对于主目标路径的横向偏离位移δb0（i），主目标路径曲率Km（k）及局部避障目标路径曲率Kmb（k）与主目标路径弧长sm（k）一一对应，主目标路径和局部避障目标路径保存在自主行驶控制器的存储介质中。

2）用采样周期T作为测量和控制间隔，当车辆沿主目标路径行驶时，用车辆的定位参考点相对于主目标路径的位置P（sm（k），δ（k））和航向角偏差β（k），及车辆转向角α（k），来表示车辆的位置。当车辆沿局部避障目标路径行驶时，仍用车辆的定位参考点相对于主目标路径的位置P（sm（k），δ（k））和航向角偏差β（k），及车辆转向角α（k），来表示车辆的位置。

3）给定Kp、Ki、Kd数值，给定T数值，给定l1、l2数值，给定K1、K2、K3数值，给定εδ1、εδ2、εβ数值。针对不同车辆上述可选参数的最佳值可由仿真计算结合实车实验来得到。

4）输入数据，δ（k）、δb0（i）、β（k）、sm（k）、smbb（i）、smbe（i）、α（k）、α（k－1）、vg（k）、Km（k）。

5）判断铲运机是否到达避障位置，当铲运机没有到达局部避障目标路径位置时，输入自主行驶控制器的横向位置偏差为δb（k），δb（k）＝δ（k）；当铲运机到达局部避障目标路径位置时，自主行驶控制器输入的横向位置偏差为δb（k），δb（k）＝δ（k）＋δb0（i），δb0（i）为局部避障目标路径相对于主目标路径的横向偏离位移。

1）局部避障目标路径的曲率Kmb（k）与主目标路径曲率Km（k）的关系为：

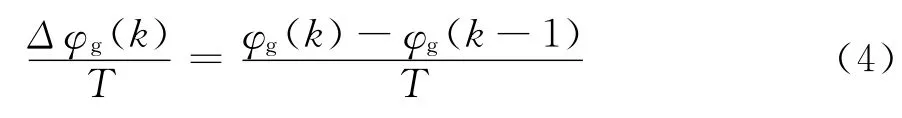
3）跟踪主目标路径时，推算计算主目标路径投影车速vm（k）的公式为：

跟踪局部避障目标路径时，推算计算局部避障目标路径投影车速vmb（k）的公式为：

4）跟踪主目标路径及跟踪局部避障目标路径时，推算计算目标路径航向角变化率的公式相同，均为：

5）跟踪主目标路径及跟踪局部避障目标路径时，计算航向角偏差变化率的公式为：

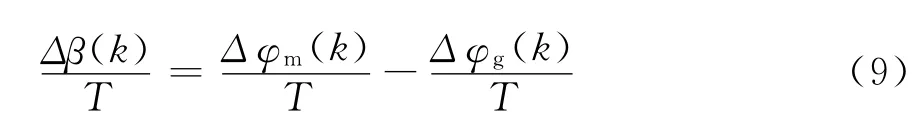
6）下一采样时刻航向角偏差β（k＋1）可通过测量数据计算得出，也可通过计算下一采样时刻航向角偏差β（k＋1）的公式计算得出：

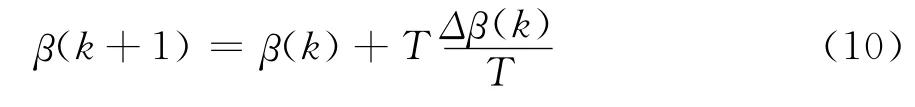
7）下一采样时刻横向位置偏差δ（k＋1）及δb（k＋1）可通过测量数据计算得出，也可通过计算下一采样时刻横向位置偏差δ（k＋1）的公式推算得出：

8）计算目标路径弧长sm（k＋1）的公式为：

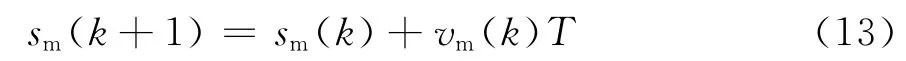
9）判断横向位置偏差δb（k）的数值，当－εδ1≤δb（k）≤εδ1时，δb（k）＝δb（k）。当δb（k）＞εδ1时，δb（k）＝εδ1。当δb（k）＜－εδ1时，δb（k）＝－εδ1。

10）计算铲运机横向位置偏差δb（k）、航向角偏差β（k）及航向角偏差变化率三种偏差融合而成融合偏差反馈信号e（k），作为PID自主行驶控制器的输入，计算融合反馈e（k）的公式为：

11）判断横向位置偏差｜δb（k）｜及航向角偏差｜β（k）｜的数值，当｜δb（k）｜≤εδ2且｜β（k）｜≤εβ同时满足时，PID自主行驶控制器才进行融合偏差反馈信号e（k）的PID控制，输出此时的转向控制电压u（k）。当｜δb（k）｜≤εδ2和｜β（k）｜≤εβ不能同时满足时，PID自主行驶控制器仅进行融合偏差反馈信号的PD控制，输出此时的转向控制电压u（k）。

融合反馈e（k）经PID控制器校正后，计算输出转向控制电压u（k）的方法为：

其中，u（k－1）为u（k）前一时刻控制电压，Δu（k）为转向控制电压的增量，且Δu（k）＝Kp［e（k）－e（k－1）］＋εKie（k）＋Kd［e（k）－2e（k－1）＋e（k－2）］，其中，e（k－1）为e（k）前一时刻的融合反馈值，e（k－2）为e（k－1）前一时刻的融合反馈值，ε为积分项的开关系数：

12）转向控制电压u（k）作为地下铲运机电液比例转向控制系统的控制电压，电液比例转向控制系统驱动转向油缸，实现铲运机自主调整转向角度，使铲运机自动跟踪目标路径。

13）当采样次数k＝1时，航向角偏差β（k），横向位置偏差δ（k）和目标路径曲线弧长sm（k）都是实测值（或由实测值计算得到），航向角偏差变化率是计算值。当k≥2时，航向角偏差β（k），横向位置偏差δ（k），目标路径曲线弧长sm（k）既可以是实测值也可是推算值，航向角偏差变化率是计算值。

应用该自主行驶控制及目标路径规划方法，进行地下铲运机自主行驶控制仿真计算。取铲运机前方驱动桥的中点到铰接中心线的距离l1＝1.270m，取铲运机后方驱动桥的中点到铰接中心线的距离l2＝1.270m，取横向位置偏差反馈系数K1＝0.20，取航向角偏差反馈系数K2＝0.55，取航向角偏差变化率反馈系数K3＝0.25，取PID的比例系数Kp＝30，取PID的微分系数Kd＝0，取PID的积分系数Ki＝18，取横向位置偏差δb门限值εδ2＝0.150m，取航向角偏差β门限值εβ＝0.06rad，取车速vg＝4km/h，取铲运机初始具有横向偏差δ0＝1m，取航向角初始偏差分别为β0＝－30°，β0＝－15°，β0＝0°，β0＝＋15°，β0＝＋30°，取初始转向角α0＝0°，目标路径为直线Km＝0m－1，铲运机从原点（0，0）开始向右运行，路径中包含一处避障路段A，A处避障距离δb0＝－3m，避障信号作用距离20m，起点为smbb（1）＝13m，终止点为smbe（1）＝33m，地下铲运机在局部大尺寸避障时的跟踪曲线图见图5，由图中轨迹曲线可见铲运机跟踪与避障控制情况良好，自主行驶控制保持优良的稳定性和快速性。

图5 地下铲运机在局部大尺寸避障时的跟踪曲线图Fig.5 Tracking curves of underground loader in local large size obstacle avoidance

4 结论

1）针对巷道内障碍物，自主行驶控制器仅需要存储横向位置避障偏离位移，及依附于主目标路径上的避障开始位置和避障结束位置数据，降低了自主行驶控制系统数据存储量和管理难度，调整和组合这三个数值，就可组成无穷多种避障路径，方便避障路径规划及避障运动控制。

2）三偏差通过非线性融合规则，形成融合偏差反馈信号，作为PID校正控制的输入信号，横向位置偏差通过限幅来慢速释放大偏差对自主行驶控制器的过大作用量；横向位置偏差及航向角偏差通过双门限控制，使得融合偏差反馈信号获得较理想的PID校正控制效果。

3）该自主行驶控制算法具有包括避障工况的跟踪轨迹偏差预测功能，在铲运机行驶过程中短时间缺少轨迹偏差实测值时，可推算出相对于主目标路径或局部避障目标路径的跟踪轨迹偏差，使自主行驶不至中断，该方法具有良好的适应性和可靠性。

［1］战凯 .地下遥控铲运机遥控技术和精确定位技术研究［J］.有色金属，2009，61（2）：107－111.

［2］高梦熊.采矿信息技术的现状与发展［J］.矿山机械，2006，34（3）：45－51.

［3］迟洪鹏，战凯，李建国，等 .地下自主铲运机定位导航关键技术［J］.矿冶，2009，18（4）：57－60.

［4］石峰，顾洪枢，战凯，等 .地下铲运机跟踪轨迹推算模型研究［J］.有色金属，2010，62（6）：66－69.

［5］石峰，顾洪枢，战凯，等 .地下无轨车辆自主导航控制器的研究［J］.矿冶，2010，19（4）：79－87.

［6］郭阳宽，王正林 .过程控制工程及仿真［M］.北京：电子工业出版社，2009.

［7］杨咸启，常宗瑜 .机电工程控制基础［M］.北京：国防工业出版社，2005.

Study on the control method of underground loader autonomous driving and obstacle avoidance

SHI Feng1，GU Hongshu1，ZHAN Kai1，LI Jianguo1，FENG Xiaohua1，GUO Xin1，LI Hengtong1，CHEN Wei2，SHI Jinpeng3
（1.Beijing General Research Institute of Mining ＆Metallurgy，Beijing 100160，China；2.Dana Management（Shanghai）Co.，Ltd.，Shanghai 200443，China；3.Anshan Iron and Steel Group Corporation，Anshan Liaoning 114007，China）

Based on the measurement data or track prediction model，the lateral position deviation，course angle deviation and the change rate of course angle deviation are calculated.By nonlinear fusion rules，the fusion deviation feedback signal is formed as the input signal of PID tuning control.The lateral position deviation and double threshold value of course angle deviation are set to improve PID algorithm.The autonomous driving control method can still maintain excellent stability and rapidity when the track deviation and driving speed change in a large range.

underground loader；autonomous driving；obstacle avoidance；control algorithm

TD422.4

A

1671－4172（2015）05－0068－08

国家高技术研究发展计划（863计划）项目（2011AA060403）

石峰（1961－），男，教授级高级工程师，流体传动与控制专业，主要从事地下无轨采矿设备研究开发。

10.3969/j.issn.1671－4172.2015.05.014