数控机床控制系统PID参数自整定方法研究*

付兰慧，周　磊，曹永军（.深圳市方元数控科技有限公司，广东深圳　58055；.广东省自动化研究所，广东广州　50000）

数控机床控制系统PID参数自整定方法研究*

付兰慧1，周磊2，曹永军2
（1.深圳市方元数控科技有限公司，广东深圳518055；2.广东省自动化研究所，广东广州510000）

摘要：数控机床在整个现代制造工业中处于核心地位，针对数控机床控制系统的三环结构设计了一种PID控制器整定方法；对数控机床位置环进行了机理建模、分析，通过RMSE评价机制得到系统模型；采用单纯形法寻优参数，并采用参数优化的方法和辨识方法提出一套自整定机制，讨论了如何选择优化准则，找出不同性能指标要求下适合的优化标准。实验证明，通过该自整定机制得到的控制器参数可以应用到数控机床的加工生产中。

关键词：数控机床；系统辨识；单纯形法；自整定；PID控制器

*广东省科技计划项目（编号：2012B011300066）；广东省产学研项目（编号：2012B091400048）

1　概述

在工业中，三环控制是数控系统控制结构所采用的经典方式，如图1所示，即电流环、速度环和位置环[1]。其中，电流环、速度环通常由驱动器来完成；位置环控制通常在运动控制器中实现，以达到更好的轨迹控制。但是，控制器参数常常是依据现场调试和经验人工进行设定的，这样就会要求操作者有一定的经验，而且会很大程度地降低加工的效率，已有的PID参数人工整定法对技术操作员的经验要求高，并且较耗力耗时。PID控制器参数整定的方法很多，基本上分为在辨识被控对象参数的基础上进行整定法、抽取过程对象输出特征点的整定法、基于模式识别的专家系统整定法及基于参数优化方法等[2-5]。本文综合采用上述方法，提出一套灵活性高、快速性好且精确度高的PID自整定机制，从而代替人工手调，本文的研究在工业自动化生产中具有重要的意义。

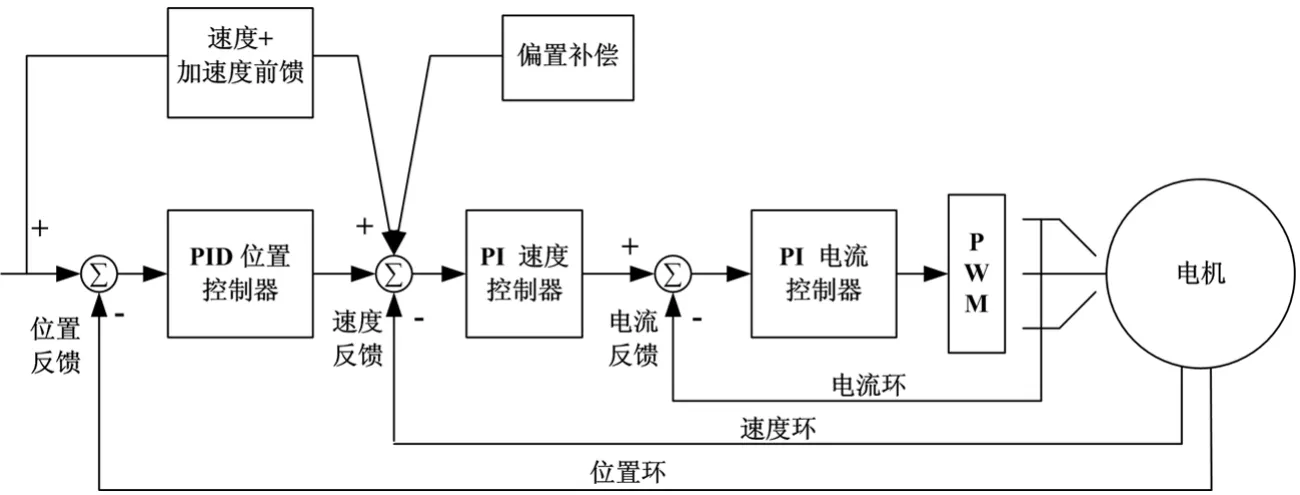
图1　三环控制的结构图

2　数控机床的建模

2.1系统建模

数控系统中，采用电机和负载的模型为：

T=ω/(Js+B)（1）

其中：B——粘滞摩擦系数；

J——系统的转矩惯量。

速度环与电流环的带宽比一般在十倍以上，因此，电流环的快速响应可近似为比例增益KI[6]，速度环的控制器一般为PI控制器，那么速度环模型可以近似为二阶模型。机械传动机构是带有比例的积分环节，因此从位置环来分析，被控对象可近似为三阶，即三阶模型是能够表述被控对象的最低阶次。此模型是文中的重点研究对象，图2所示为其结构框图，其中CT为伺服电机转矩系数。

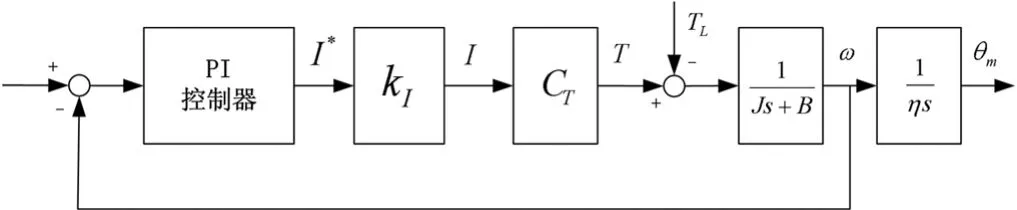
图2　被控对象结构框图

2.2系统辨识

输入信号选用频率在0~100 Hz的扫频信号，采用最小二乘法进行辨识。在前面建模得出，系统物理模型是三阶连续域模型，但数控系统是离散控制系统，依次引入四个模型，如式(2)所示。通过实验验证的方法来选取适当的离散模型。

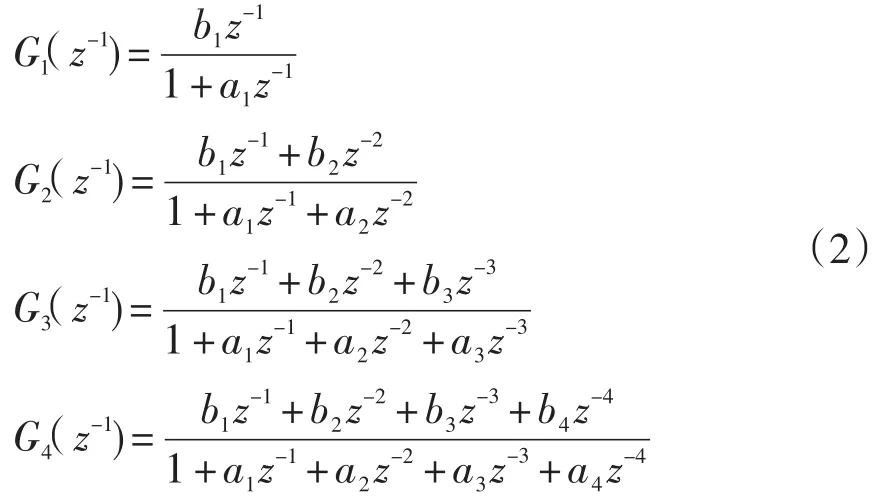
对四个阶次的模型进行辨识，分别将估计输出与实际采集的输出进行对比，结果如图3所示。

将不同阶次的模型与平台实际输出的均方根误差（RMSE）列在表1中。

从中容易看出，能准确表达实际系统需要选择三阶或以上的模型。

为方便后边章节引用，以四阶无延迟模型为例，其传递函数为：

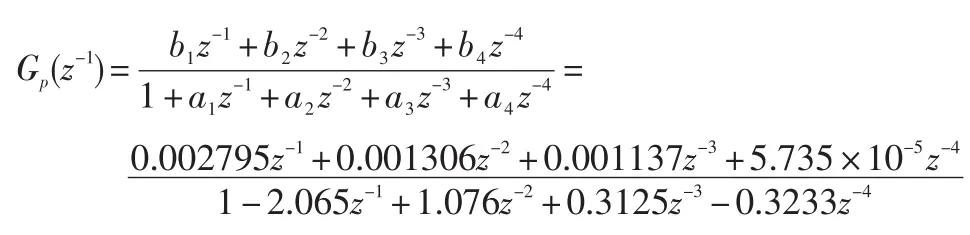
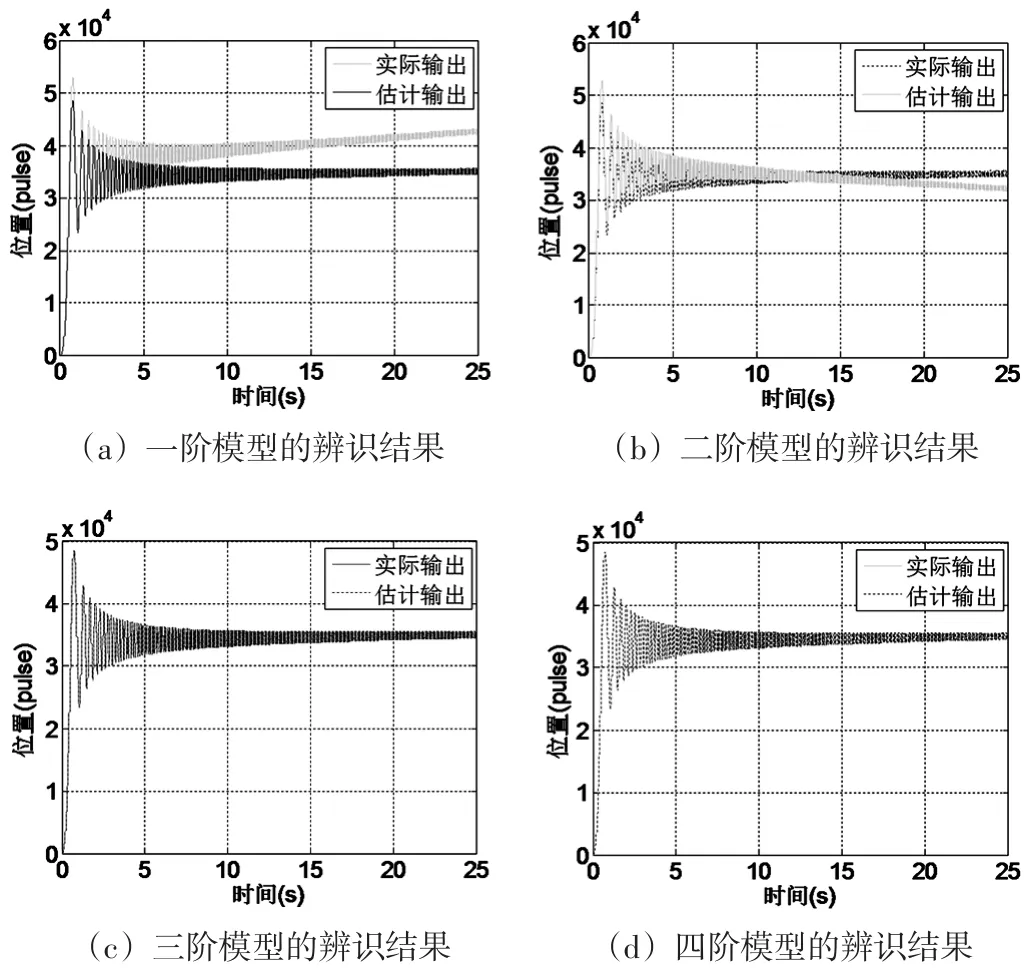
图3　模型的辨识结果

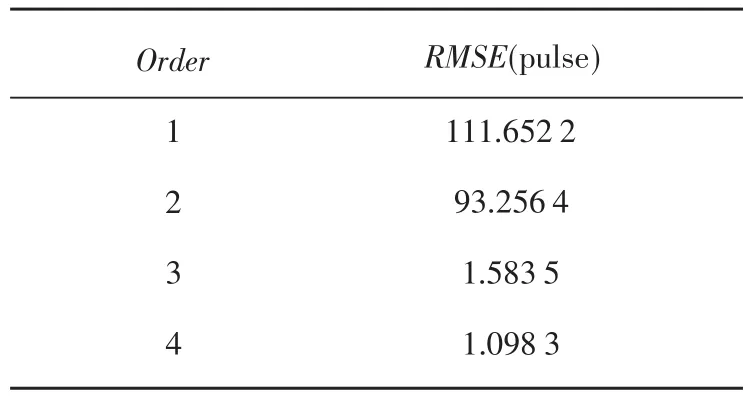
表1　四个阶次模型的RMSE

3　基于参数优化的自整定方法

3.1PID控制器的结构

使用增量式PID控制算法[7]，可得：

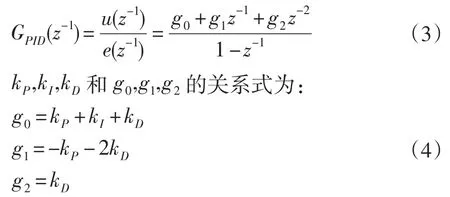
基于上一节建模结果，位置环的结构框图如图4所示。

图4　位置环的结构框图

3.2PID控制器参数自整定机制

接下来基于单纯形法对控制器进行参数寻优。Gp(z-1)为被控对象的传递函数，GPID(z-1)为控制器的传递函数，根据二者可以得到跟踪误差e(k)的离散公式：

y(k)=GPID(k)Gp(k)e(k-1)

e(k)=r(k)-y(k)（5）

r(k)是输入，为阶跃信号。

系统在参数寻优过程中，将描述优化准则的目标函数设为F(m)，即：

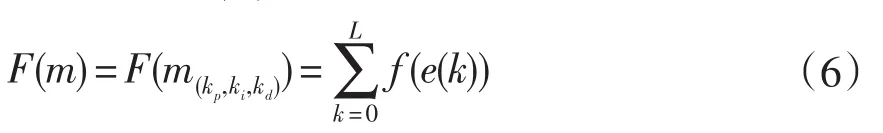
F(m)与跟踪误差相关，式中，m为三维空间里的坐标，kP,kI,kD的数值为m的坐标值，L是r(k)的数据长度，f(e(k))为控制器跟踪误差的函数。

PID参数的自整定即对kP,kI,kD的参数值进行优化，因此，满足系统性能的PID值即是优化后的最终结果，那么，PID参数自整定的问题可写为下式：

在该优化问题中，PID参数值的选择要满足系统稳定的条件范围，这个范围称为可行域Q：

kP，kI，kD∈Q（8）

PID参数的寻优机制如图5所示：

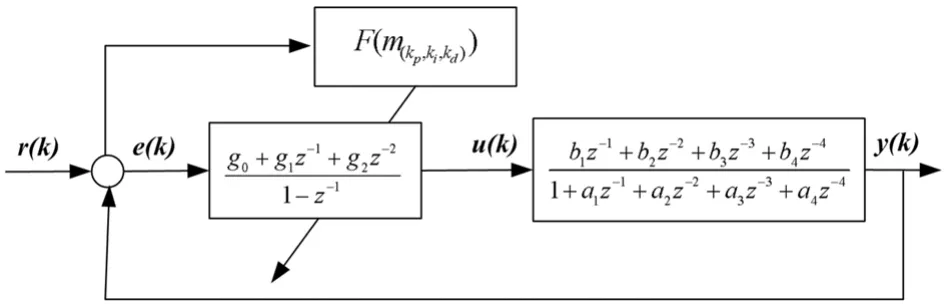
图5　PID参数的寻优机制

PID寻优流程如图6所示，PID控制器参数的自整定流程图如图7所示。

4　优化准则

优化准则的选取在PID参数自整定的过程中尤为重要，我们选用常用的几种方法对运动控制实验平台进行参数优化并作分析，找到能够描述系统性能指标状态的最佳优化准则。

（1）误差平方的积分准则(ISE)：

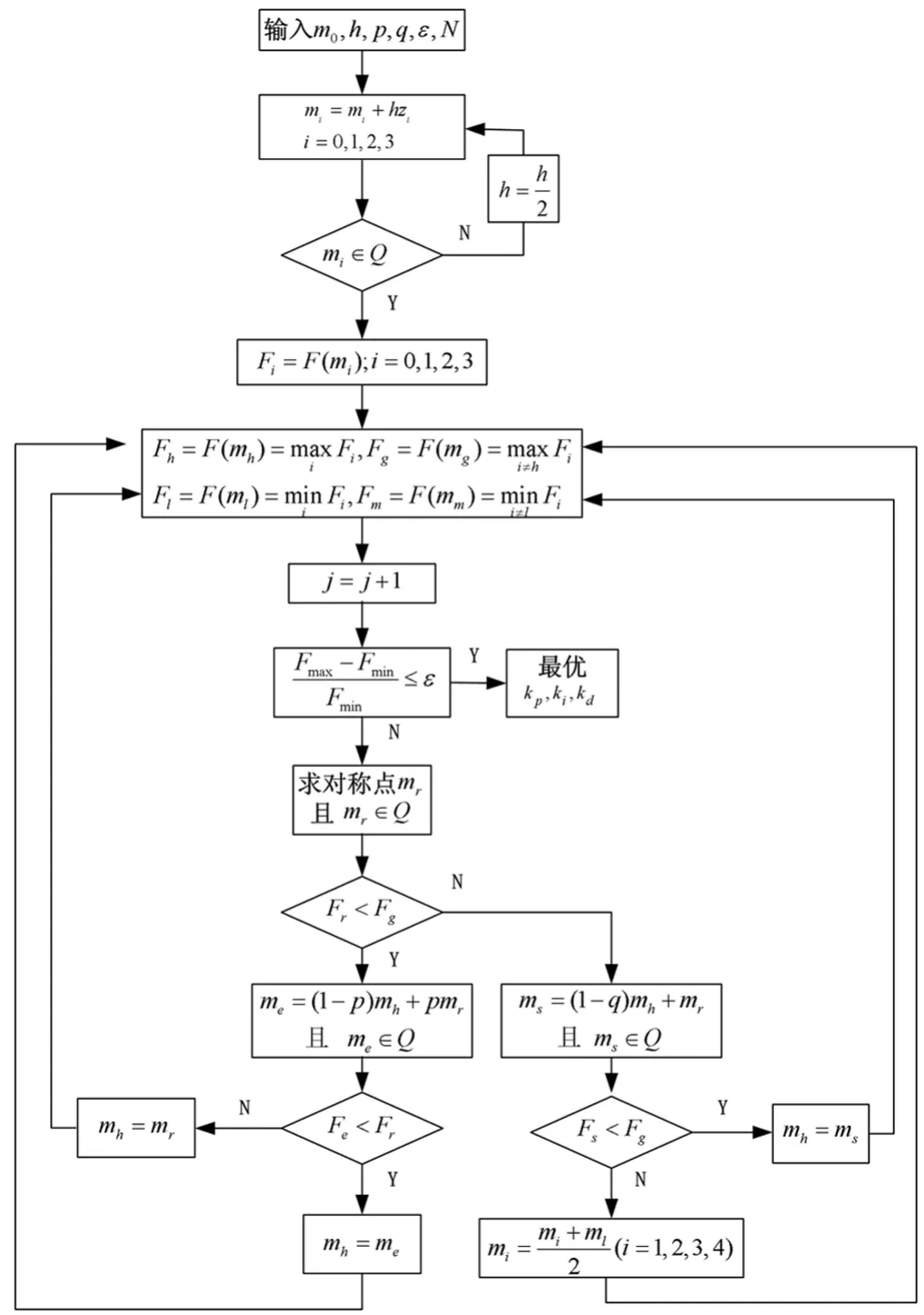
图6　寻优算法的流程图

系统在ISE准则下优化PID的阶跃响应如图8所示。从曲线中可以看到系统存在很大的超调。

（2）误差平方的矩的积分准则(ITSE)：

系统在ITSE准则下优化PID的阶跃响应如图9所示。可见，超调明显减小，调整时间也明显降低。

（3）误差绝对值的矩积分准则(ITAE)：

系统在ITAE准则下优化PID的阶跃如图10所示。通过对比，ITAE准则下，调整时间进一步缩短，系统超调小、快速性好、平稳性提高。

（4）广义平方误差积分准则(GISE)：

系统在GISE准则下优化PID的阶跃响应如图11所示，系统没有超调。

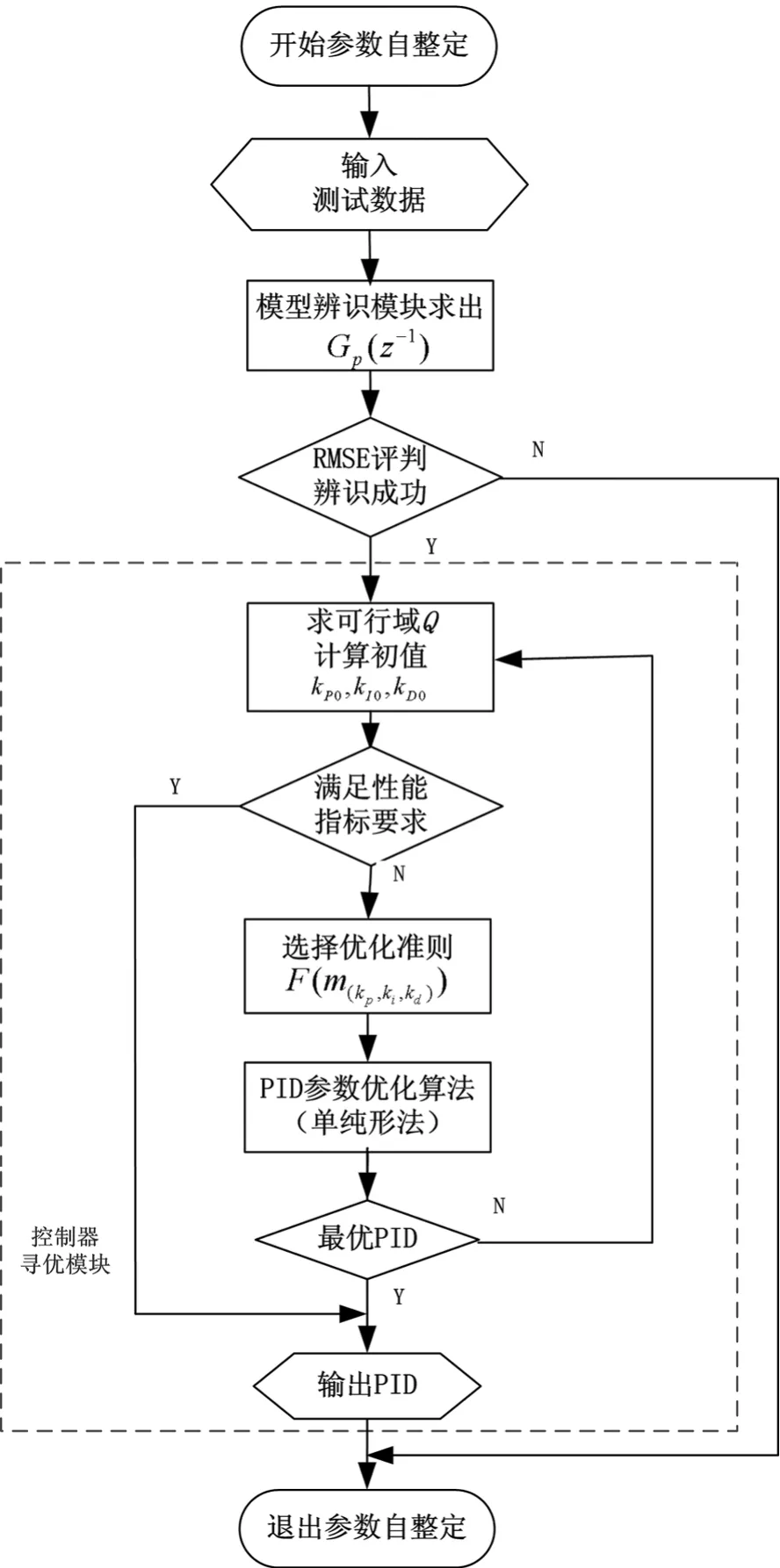
图7　参数优化自整定的流程图

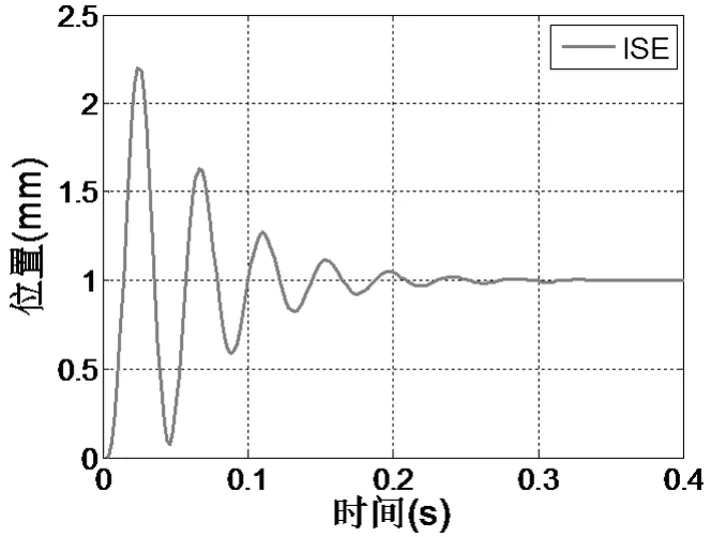
图8　基于ISE准则的阶跃响应

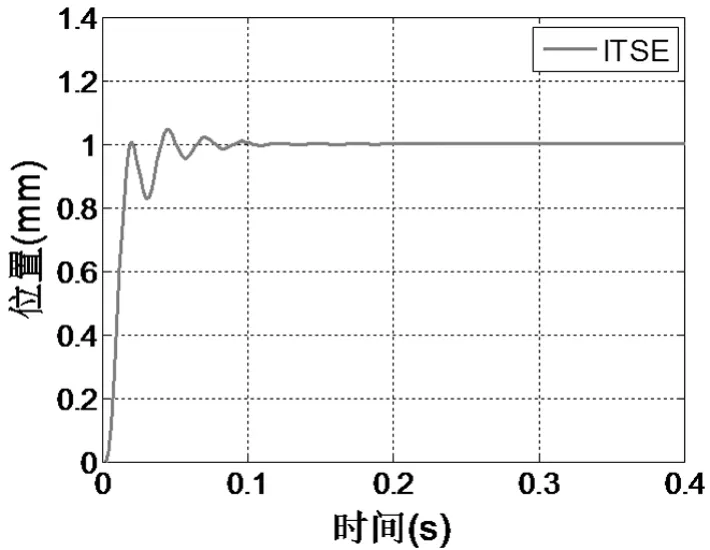
图9　基于ITSE的阶跃响应

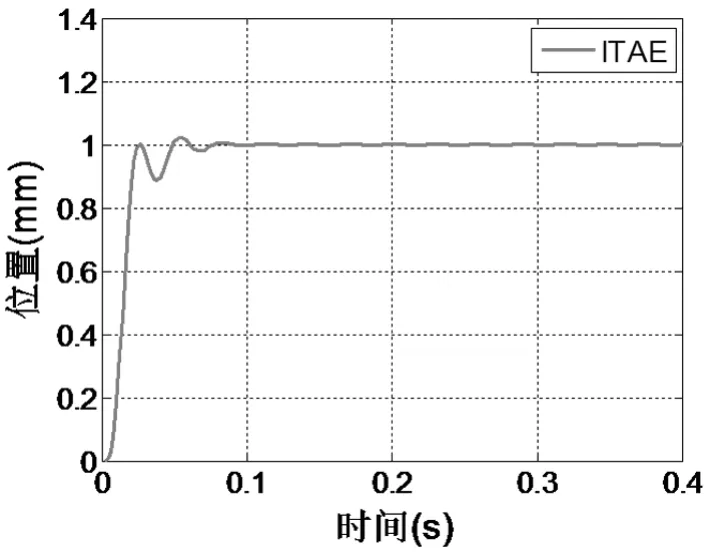
图10　基于ITAE的阶跃响应

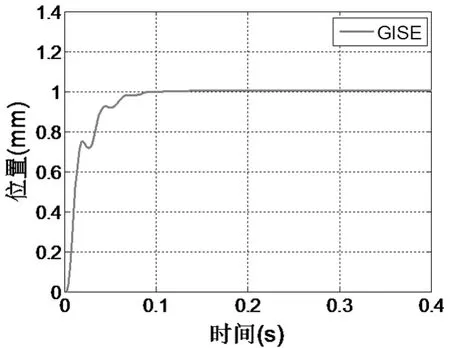
图11　基于GISE的阶跃响应

（5）基于时间的广义误差积分准则：

系统在GITSE准则下优化PID的阶跃响应如图12所示。GITSE准则相比GISE准则，将时间的权重考虑进去，提高了系统的响应速度，同时缩小了系统的稳态误差。

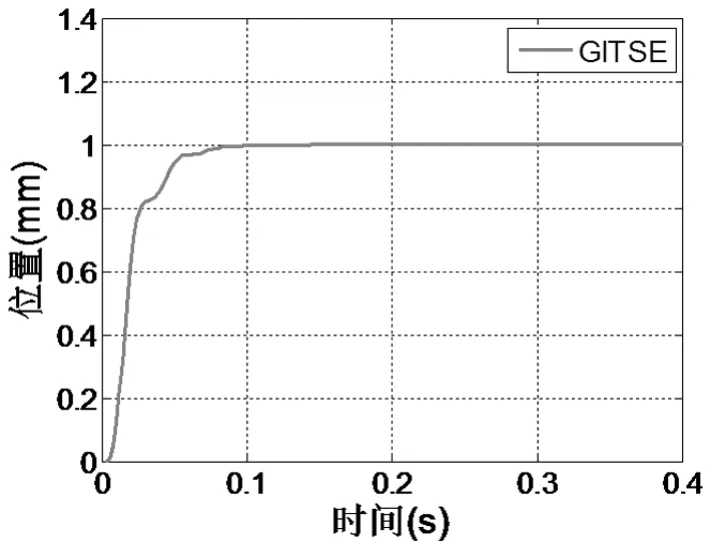
图12　基于GITSE的阶跃响应

将优化结果进行对比，见表2所示。Td为延迟时间、ts为调整时间、tp为峰值时间，tr为上升时间，σ%为超调量，N为振荡次数。

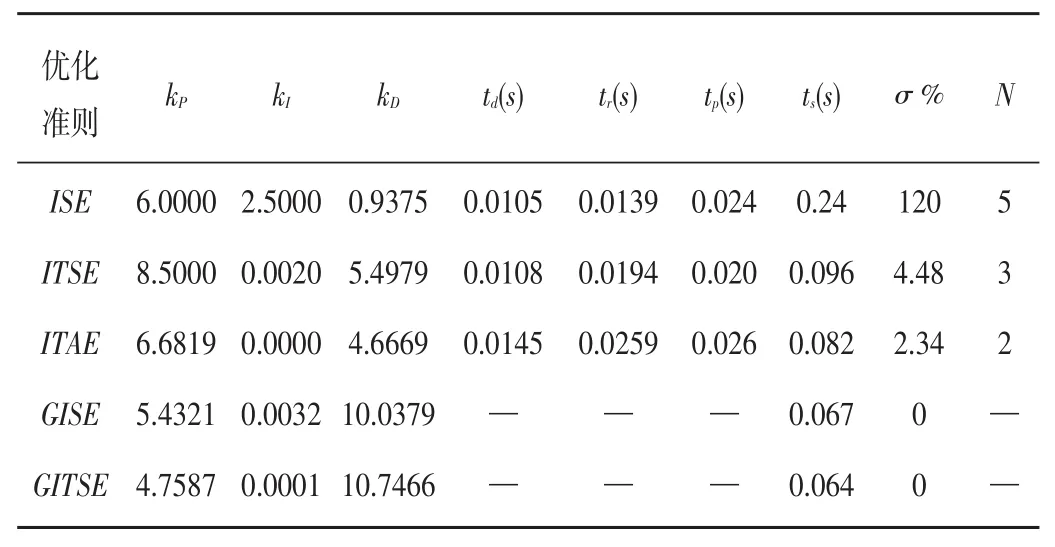
表2　优化结果对比

系统的快速性可以从td、ts、tp和tr来分析，系统的平稳性从σ%和N来分析。ISE由于ts长同时σ%大而不被采用。ITSE的tr较短，σ%适中，在平稳性一般但快速性高的系统中可以采用。ITAE的振荡次数少，σ%小，ts适中，在对平稳性能和快速性能都有要求的系统中可以采用。GISE和GITSE以其ts最短并且无超调的特点，在平稳性能和快速性能要求都很高的系统中可以采用。

5　实验

选取一台小型的三轴雕铣机床作为实验平台，将自整定算法在实际机床上进行验证。基于GITSE优化准则的进行寻优与手调PID结果进行对比，如表3所示。

表3　三轴雕铣机床的PID参数

图13为传统手调方法和PID自整定方法的加工对比，加工实验均为曲面加工，加工速度均为每分钟两米。从中可以看出，加工效果在曲率小的时候差别并不明显，而在曲面的曲率较大的地方，自整定要比手调效果好很多，另外，在时间上，自整定算法加工的时间要比人工手调方法的加工时间少很多。

图13　自整定PID与手调PID的加工结果对比

6　结论

本文针对数控机床控制系统位置环设计了一种PID控制器自整定方法。通过RMSE评价机制得到数控机床位置环模型，基于GITSE优化准则并采用单纯形法进行了参数寻优。实验证明，该PID自整定机制可以取代传统的人工手调，在数控系统的生产加工中得到应用。

参考文献：

［1］吴黎明.数字控制技术［M］.北京：科学出版社，2009.

［2］刘震，姜学智，李东海.PID控制器参数整定方法综述［J］.电力系统自动化，1997，21（8）：79-83.

［3］Eric P，Andre P.Development and Evaluation of an Au⁃to-tuning and Adaptive PID Controller［J］.Automati⁃ca，1996，32（1）：71-82.

［4］Dwyer A O.Handbook of PI and PID Controller Tuning Rules［M］.London：Imperial College Press，2009：44-51.

［5］Wilson D I.Optimal Control［M］.Sweden：Karlstad University Press，2000：56-67.

［6］M.C.Tsai，I.F.Chiu，M.Y.Cheng.Design and Imple⁃mentation of Command and Friction Feed-forward Con⁃trol for CNC Motion Controllers［J］.IEE Proceedings Control Theory Applications，2004，151（1）：13-20.

［7］陶永华.新型PID控制及其应用［M］.北京：机械工业出版社，2002.

(编辑：向飞)

Study of PID Self-Tuning Method in CNC Control

FU Lan-hui1，ZHOU Lei2，CAO Yong-jun2
（1.Fangyuan NC Tech.Co.，Ltd.，Shenzhen518055，China；2.Guangdong Institute of Automation，Guangzhou510000，China）

Abstract:CNC system is the core of the modern industry.In this paper，we proposed a self-tuning method of PID controller in CNC control system.The position loop is modeled and analyzed with RMSE evaluation mechanism.Based on simplex method，use parameter optimization and identification to establish the self-tuning method.Find out the optimal criteria for different performance requirements by discussing how to choose the optimal criteria.The experiments provide that the self-tuning method can be applied to the processing and production of CNC.

Key words:CNC；system identification；simplex method；self-tuning；PID controller

作者简介：第一付兰慧，女，1987年生，河南人，硕士研究生，工程师。研究领域：运动控制。已发表论文2篇。

收稿日期：2015－07－28

DOI:10.3969/j.issn.1009-9492.2015.08.024

中图分类号：TG659

文献标识码：B

文章编号：1009－9492 (2015 ) 08－0087－05