基于空间距离的快速模糊C均值聚类算法

王军玲 ，王士同 ，包 芳 ，周建林

1.江南大学 数字媒体学院，江苏 无锡 214122

2.江苏省信息融合软件工程技术研发中心，江苏 江阴 214405

3.江苏省江阴职业技术学院 计算机科学系，江苏 江阴 214405

1 引言

图像分割被广泛应用于诸多领域，例如机器视觉、目标识别、地理和医学图像等。一般说来图像分割是根据灰度或者纹理信息等特征将图像分割成一些连续不重叠区域的过程。模糊C均值聚类算法就是经典的图像分割算法之一[1-4]，相对于硬性聚类[5]它的优点在于对每个像素引入了一个归属隶属度，使得分割结果更符合现实状况。但是在模糊C均值聚类算法中，它采用的是考察像素到聚类中心的欧几里德距离，即它不考虑图像纹理等任何临近空间信息，使得算法对噪声、孤立点很敏感。也有很多学者将考察像素临近空间信息引入原始的FCM算法来改进分割性能[5-7]，Tolia和Panas提出了一个基于规则系统的Sugeno-type的FCM算法[6]以改进模糊分割结果。Pham[8]通过在隶属度上引入一个空间惩罚机制，并且允许采用空间光滑隶属度函数进行估计从而产生了类似于原始FCM的迭代算法。Ahmed[9]等人修正了FCM的目标函数用来弥补灰度分布不均衡并且将临近元素的影响代入计算，即产生了FCM_S算法。由于FCM_S算法每次迭代的过程中临近像素的信息都要参与运算无形中增加了时耗，陈宋灿[10]等提出了在进行迭代之前先计算出对应的均值滤波图像或是中值滤波图像以加快聚类速度，提出了FCM_S1、FCM_S2算法，两种算法在一定程度上提高了算法的聚类性能。但是这几种算法中都含有一个重要的参数a，参数的确定需要依据噪声类型经过大量的实验经验来选择，并且算法耗时随着图像变大而不断增加。2007年，刘一光[11]等人提出的K-NS分类器在分类过程中，采用了空间距离公式使得分类器相对于经典的KNN算法[12]表现出了更好的性能。

针对以上的经典算法中所出现的问题，本文提出了基于空间距离的快速模糊C均值聚类算法，借鉴刘一光[11]等人的空间距离公式，使得临近像素的灰度与位置信息同时参与考察像素与临近像素间的相似度Sij的计算，利用该相似度得出临近像素制约图像，并对临近信息制约图像进行灰度统计后再聚类[13]，从而有效减少了聚类耗时，体现出了良好的分割性能。

2 FCM算法原理及其优化

FCM算法核心思想是首先将一个数据集X分为c个模糊组，然后求每组的聚类中心，当相似性指标的目标函数Jm达到最小时，元素就将被划分给隶属度最大的那个分组。FCM算法的目标函数如下所示[14]：

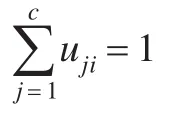
（1）设置c，m和ε的初始值。

（2）初始化模糊隶属度矩阵U(0)。

（3）设置循环计算器b的值。

（4）使用U(b)更新这c个分组的中心：

（5）更新隶属度矩阵U(b+1)：

（6）如果 {U(b)-U(b+1)}＜ε则停止计算；否则设置b=b+1，转到（4）。

若算法应用于图像分割则参与运算的是像素的灰度，可以看出该算法没有考虑考察像素临近像素的信息，图像会受时间、光照及白噪声的影响，从而导致这些受噪声影响的像素被误分类，即对孤立点敏感。

为了克服对孤立点敏感这一缺陷，也有学者将临近像素的灰度信息引入目标公式，但是每次迭代都要计算考察像素的邻近信息，具有代表性的如FCM_S算法，导致算法耗时量大。进一步优化的FCM_S1算法在算法开始迭代之前得到滤波图像，然后原图像和相应的均值滤波图像同时参与算法的计算，不仅减少了运行时间并且增强了算法对高斯噪声的抗干扰能力。然而，FCM_S1算法对受脉冲噪声影响的图像分割效果不太理想，FCM_S2算法使用中值滤波图像来代替FCM_S1算法中的均值滤波图像很好的解决了这个问题，但该算法对较强均匀噪声的抵抗性较弱。综上，由经典的FCM算法改进而来的FCM_S、FCM_S1和FCM_S2算法的共同点是都考虑了临近像素的灰度信息，并采用参数a来控制其对考察像素的影响程度，这样每个考察像素的临近像素对其影响程度是一致的，都由a来决定，算法一定程度上减弱了噪声点对分割结果的影响，但是现实中噪声点分布状况是随机的，临近像素对考察像素的影响也应因是否受噪声干扰和位置差异而有所不同，所以算法对受不同噪声干扰图像分割的鲁棒性还有待进一步提高。在这些经典的算法当中采用的都是欧几里德距离，而欧几里德距离对球体数据聚类具有较好的效果。刘一光学者提出的空间距离公式[11]在KNN算法中获得了很好的分类效果，本文尝试通过空间距离公式将临近像素信息引入标准的FCM算法，从而来弥补噪声分布不均匀等位置因素所带来的缺陷，并且在对临近制约图像灰度统计的基础上进行聚类，以适用于大图像的分割。

3 空间距离公式

在FCM算法中都是单纯的采用欧几里德距离，通过不断的迭代，使得聚在一类里面的像素灰度与中心像素灰度差别最小，而获得最优结果。致使考察像素临近像素信息无法包含在内，如果图像受到噪声干扰，将导致该像素误分类。尝试引入考察像素与临近像素的相似度，将临近像素的制约信息也代入目标公式以提高算法的抗干扰性能，要提出的新算法中相似度的计算采用了刘一光[11]等人提出的空间距离公式，不仅包含临近像素的灰度信息并且包含了位置信息。空间距离公式[11]的原理如下所示。

3.1 空间距离

若把一条线或一个曲面看作流型拓扑空间，真实空间中相互独立的若干元素通过一个具有足够高阶数的函数可以转换到一个流型拓扑空间。依据给定的一组训练样本，可以得到多个拓扑空间同时包含这些点。

设sq为考察元素i的向量，Ni为任意k个向量元素组成的数据集；Mi是由Ni中的元素通过转换函数得到的某个拓扑空间；Si是Ni中元素的分布空间；xij表示元素i的临近数据集Ni中的第j个元素向量；数据集Ni与Mi之间的关系如图1所示。

图1 数据集Ni及其所形成的拓扑空间Mi关系图

每个不同形式的Mi的重合部分几乎都由空间Si包围着，在空间Si中每个点都可以被近似看作是数据集 Ni中的一个元素，则在图1中dsq→Ni是从sq到空间Si的距离。首先建立一个以Ni中元素向量为边的一个超平面体，当Ni是列满秩时，超平面体的容量是[]：

VNi和之间的关系如图2中例子所示：

由公式（4）～（6）推出：

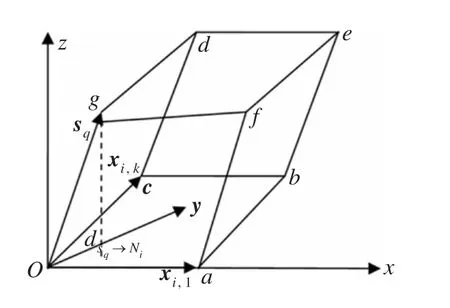
图2 考察元素点向量sq到空间Mi距离的几何展示

虽然的求解具有对称性，但是它不满足三角不等式[11，16]，因此不能作为样本集合距离度量标准，需在核函数的作用下核化将空间距离公式转化为可以使用的量度标准。

其中μ是用来量化正则化的程度；I是对应的单位矩阵。

3.2 空间距离公式的核化

从函数的角度分析，公式（8）在核函数 ker(x，y)(x，y∈Rn)的作用下可以满足量度空间的要求：

其中 ker(x，y)是由φ(x)和φ(y)两个映射确定的隐函数。对sq、x间的欧几里德距离进行核化得：

空间距离核化时分别用φ(sq)和φ(Ni)代替公式（8）中的sq和x可以转化为：

用公式（11）代替公式（8），Tikhonov正则化项μI用于避免核矩阵ker(Ni，Ni)线性相关，确保公式计算的稳定性。

4 SFGFCM算法

4.1 相似度Sij的计算

一些学者在2007年提出了相似度的计算，根据考察像素i与临近像素j的灰度差与落在临近窗口内所有临近像素与考察像素灰度差的平均比值作为相似性度量来计算Sij，并且将其采用指数函数进行归一化，则其定义为如下形式：

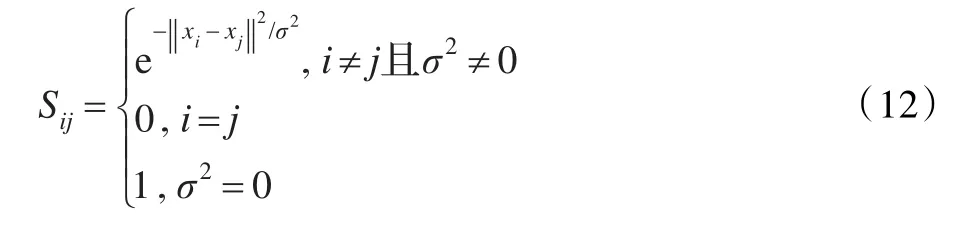
若将σ看作考察像素点到临近像素点所形成曲面流型体的距离，采用上文提到的核化的空间距离公式将空间信息包含进来，即将临近像素的位置信息也包含在内，进一步对相似性度量Sij进行优化，则可变化成如下形式：

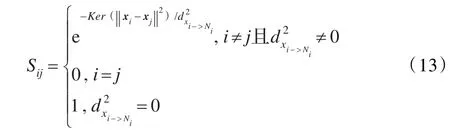
4.2 SFGFCM算法

在引入临近像素相似度Sij后可以得到一幅同时包含临近像素空间灰度信息的临近信息制约图像ξ，图像上像素点i的灰度值计算方式如下[18]：

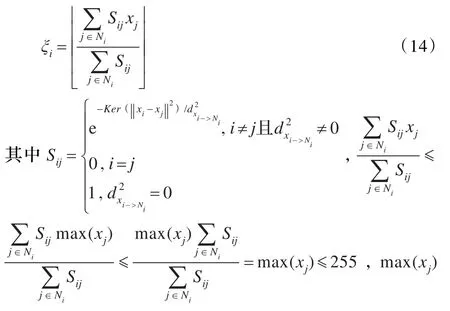
表示像素i的临近像素中的灰度最大值，ξi∈[0，255]表示临近信息制约图像中像素i的灰度值（显然大于零），它同时包含原图像中像素i的临近像素灰度与空间信息。将临近信息制约图像的灰度级进行统计，并对处于同一灰度级的像素赋予相同的隶属度，聚类的目标函数就变成了如下形式[19]：

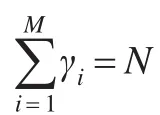
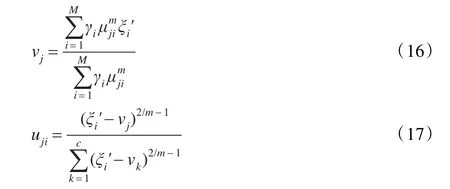
SFGFCM算法的求解过程如下：

（1）初始化聚类中心数目c，模糊指数m和停止迭代最小差值条件ε；

（2）随机初始化模糊划分矩阵；

（3）设置迭代次数b=0；

（4）通过公式（16）更新聚类中心点灰度；

（5）通过公式（17）更新划分隶属度矩阵；

（6）当{U(b)-U(b+1)}＜ε算法收敛停止计算，否则，令b=b+1并且转向（4）。

改进后的迭代算法类似于原始的FCM算法，但是参与聚类的灰度值包含了更多临近像素空间及灰度信息，可以根据每个临近像素的灰度及位置信息而计算出相似度Sij而无需过多的考虑平衡二者的关系问题。加之是对邻近信息制约图像的灰度统计后进行聚类，使得算法的聚类时间取决于邻近信息制约图像的灰度级数，而不是图像的像素个数，从而该算法适用于大型图像的分割。因为一般的图像灰度是8位二进制码（即256个灰度级），而一副图像的灰度级数M远远小于图像的像素个数N，执行时间将大大的降低。

5 实验与性能分析

本章通过在真实和合成图像上的分割性能和分割效率将FCM与文中的SFGFCM算法进行比较。实验运行环境为CPU Inter双核2.1 GHz，2 GB内存，Matlab7.1。

采用分割准确性SA对两种算法的抗噪性能进行比较，这里的SA指被正确分割的像素点个数占参加图像分割的像素点总数的比例[13]：

式中c是聚类数，Ai代表的是由算法划分到第i组的像素集，Ci代表在涉及到的分割图像中属于第i组的像素集。

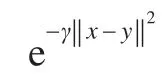
表1 被8%高斯噪声干扰的syn图像采用SFGFCM算法分割结果 （%）

图3 被8%高斯噪声干扰的syn图像采用SFGFCM算法分割结果

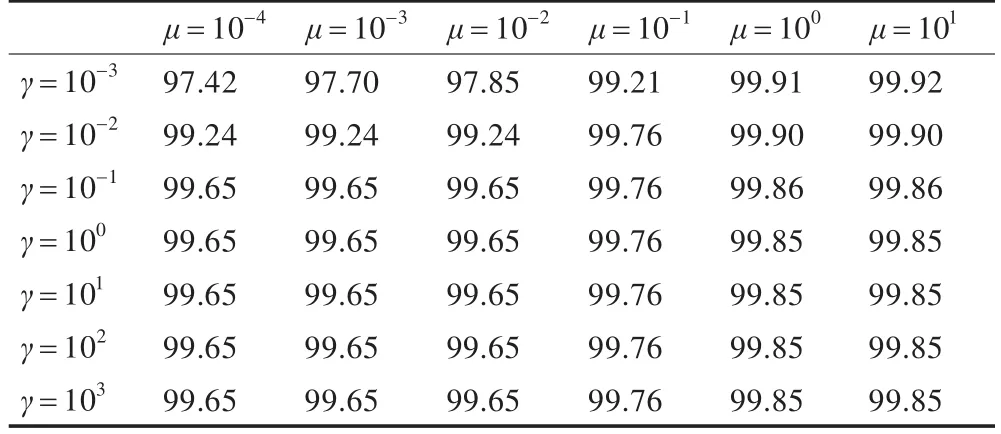
表2 被8%均匀噪声干扰的syn图像采用SFGFCM算法分割结果 （%）

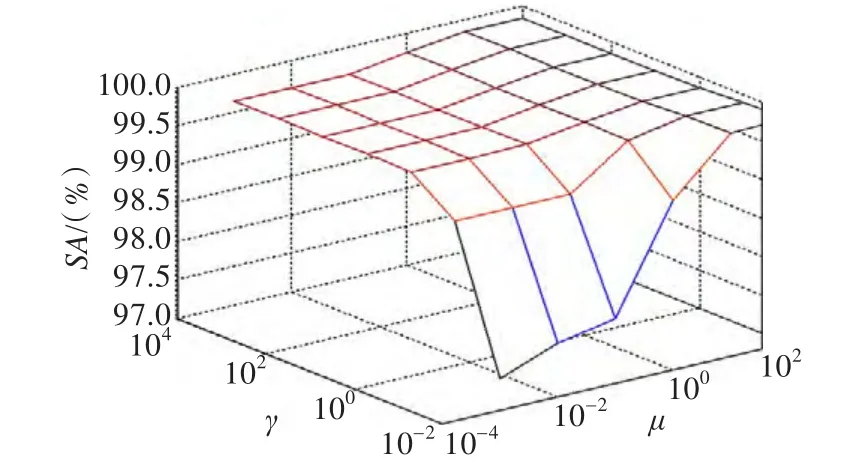
图4 被8%均匀噪声干扰的syn图像采用SFGFCM算法分割结果

表3 被8%椒盐噪声干扰的syn图像采用SFGFCM算法分割结果 （%）

图5 被8%椒盐噪声干扰的syn图像采用SFGFCM算法分割结果

实验1首先用该算法对受不同性质（高斯噪声，均匀噪声和椒盐噪声）不同程度噪声干扰的合成图像syn进行分割，其中设置c=2。图6显示了被20%的高斯噪声干扰的合成图像syn，以及FCM、SFGFCM算法分割的效果。可以观察到，FCM算法受到噪声干扰较严重，SFGFCM算法几乎可以不受噪声影响，并且很好地保留了边缘信息，体现出了其鲁棒性。通过对SA%的计算（表4）更进一步说明了该优势。

图6 对合成图像的分割效果

表4给出了两种算法在合成图像syn受到不同程度噪声干扰的情况下的分割精度，每个实验都采用了五组随机初始化值，取其平均值作为实验结果，数据很清楚的显示出SFGFCM算法比FCM算法有较好的鲁棒性。

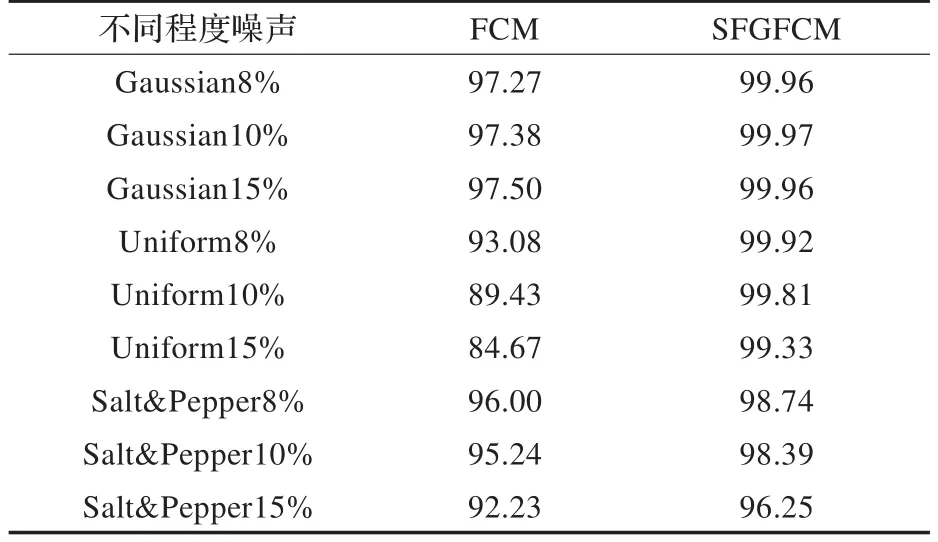
表4 两种算法在合成图像上的分割精度（%）

实验2从公式（13）可以看出，对噪声和孤立点的抵抗性主要依赖于Sij的定义，在没有噪声的先验知识的情况下，Sij是自动确定的而不是人工设定，被噪声干扰的Sij应该是尽量的小，从而噪声的干扰可以忽略。在SFGFCM算法中Sij对于不同的临近像素可以自适应的改变，从而体现出较强的抗干扰性。孤立点和噪声的出现主要有下两种情况：

（1）考察像素不是噪声点，而落在考察像素临近窗口内的某些像素一定程度上受到了噪声的干扰，那么受到噪声干扰的像素灰度值和其他像素的灰度值差异性较大，根据公式（13）可知，相应的Sij值也应该小。因此计算出的加权和也会受到噪声点的影响较小，体现出来的也就是对噪声点和孤立点有较强的鲁棒性。图7是某像素3×3临近窗口及对应像素的相似度，清晰地说明了这个问题，例如图中第一个灰度值为100的像素在右边框中对应的相似度Sij为0.123 1。

图7 一个3×3的被噪声干扰的窗口及对应的相似度

（2）当考察像素是一个噪声点，而落在临近窗口内的其他像素都是相似的，这样的情况下由于考察像素到临近像素点所形成流型空间的距离较大，从而导致临近像素对应的Sij都较小且几乎是相同的，因此计算出来的ξi受到的考察像素的影响较小，如图8所示。

图8 一个3×3的被噪声干扰的窗口及对应的相似度

以上两个例子验证了新算法的鲁棒性。

实验3用两种算法分别对受到30%椒盐噪声干扰的图像进行图像分割，最后的聚类分割效果如图9、10所示。eight图像分割过程中c=3；wheel图像分割过程中c=4。从最后的实验结果可以看出，FCM算法的分割效果很大程度上受到了椒盐噪声的影响，而本文提出的SFGFCM算法显现出一定的抗干扰性。

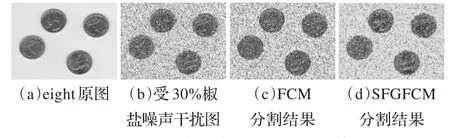
图9 两种算法在图像eight上的分割结果图

图10 两种算法在图像wheel上的分割结果图

另外，采用这两种算法对图6～图11中涉及到的图像进行了分割。在实验之前对这些图像使用不同程度（8%、10%、15%）的高斯、均匀和椒盐噪声进行干扰，按照以下方法得出计算分数[13]：

其中c是聚类分组数，Ai代表的是受噪声干扰图像通过算法计算划分到第i组的像素集合，Ci代表的是原图像通过算法划分到第i组的像素集合，r相当于是一个模糊相似度衡量，表明了Ai和Ci相等的程度，r越大越好。实验结果如表5所示。

表5 两种算法在各种图像上的计算分数（%）

在表5中每个实验都采用了五组不同的随机初始值，被同类型噪声干扰的图像的计算分数取平均值，作为最后结果。

实验4图11则展示了本文所提算法在一些自然图像上的分割效果，每组图片中左边是原图，右边显示的是分割后的效果图，每组图片都随机采用了五组不同的初始值，每次分割后效果都是一样的。

实验5最后在对各种算法进行相同的优化之后，图12显示了两种算法的对不同大小图像的平均耗时，每个大小的图片都用采用五种不同的图片和随机的初始值，聚类的数目从2到5。从图中可以看出文中的两种算法随图像大小的耗时变化。

图11 SFGFCM算法在自然图像上的聚类分割结果

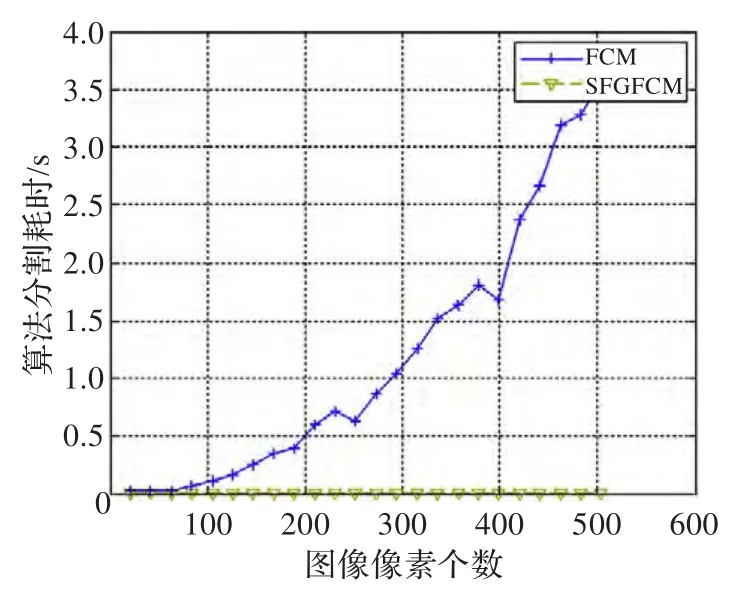
图12 两种算法对不同大小图像的耗时

耗时除了受编程风格的影响，起决定性的还是算法的思想，FCM算法的时间复杂度是O(NcI1)（其中N是一幅图像中像素的个数，c是聚类数目，I1是每次分割的迭代次数）；本文算法SFGFCM的算法复杂度是O(McI2)（其中M是一幅图像中出现的灰度等级数，c是聚类数目，I2是每次分割的迭代次数）。同一幅图像中，灰度等级最多是256，在一般规模的图像中灰度等级数是远小于像素的个数的，并且由于灰度的范围都在[0，255]之间，从而采用不同的算法分割图像最终的迭代次数不会有太大的差别（实验显示迭代次数只相差一两次），因此算法的耗时就取决于N、M的大小，由此SFGFCM算法在保证了算法分割性能的同时，减少了时间损耗。

6 结束语

本文提出了一个基于空间距离的快速FCM算法（即SFGFCM），该算法采用空间距离计算出考察像素与其临近像素的相似度Sij，使得在迭代计算的过程中不仅引入了临近像素的灰度信息而且还隐含了临近元素的位置信息，并且使得灰度与位置等空间信息得到了很好的平衡；在得到邻近信息制约图像之后对其灰度级进行统计之后进行聚类，从而使得聚类耗时大大减少。与传统算法相比，不仅保证了图像分割的性能，并且还减少了耗时；通过对一系列的合成和自然图像进行分割实验，与经典的FCM 算法相比，增强了对外界噪声的抗干扰能力，具有更强的鲁棒性，且该算法更适用于大幅图像聚类。

[1]Udupa J K，Samarasekera S.Fuzzy connectedness and object definition：theory，algorithm and applicationsin image segmentation[J].Graph Models Imageprocess，1996，58（3）：246-261.

[2]Yamany S M，Farag A A，Hsu S.A fuzzy hyper spectral classifier for automatic target recognition（ATR）systems[J].Pattern Recognition Lett，1999，20：1431-1438.

[3]Yang M S，Hu Y J，Karen C R，et al.Segmentation techniques for tissue differentiation in MRI of ophthalmology using fuzzy clustering algorithms[J].Magnetic Resonance Imaging，2002，20（2）：173-179.

[4]Karmakar G C，Dooley L S.A generic fuzzy rule based image segmentation algorithm[J].Pattern Recognition Lett，2002，23（10）：1215-1227.

[5]Pham D L，Prince J L.An adaptive fuzzy c-means algorithm for image segmentation in the presence of intensity in homogeneities[J].Pattern Recognition Lett，1999，20：57-68.

[6]Tolias Y A，Panas S M.On applying spatial constraints in fuzzy image clustering using a fuzzy rule-based system[J].IEEE Signal Process Lett，1998，5：245-247.

[7]Liew A W C，Leung S H，Lau W H.Fuzzy image clustering incorporating spatialcontinuity[J].InstElec Eng Vis Image Signal Process，2000，147：185-192.

[8]Pham D L.Fuzzy clustering with spatial constraints[C]//IEEE Proceedings of the International Conference Image Processing，2002：65-68.

[9]Ahmed M N，Yam S M，Mohamed N，et al.A modified fuzzyC-means algorithm for bias field estimation and segmentation of MRI data[J].IEEE Trans on Med Imaging，2002，21：193-199.

[10]Chen S，Zhang D.Robust image segmentation using FCM with spatial constraints based on new kernel-induced distance measure[J].IEEE Transactions on Systems，Man and Cybernetics，2004，34（4）：1907-1916.

[11]Liu Yiguang，Sam Shuzhi，Li Chunguang，et al.k-NS：a classifier by the distance to the nearest subspace[J].IEEE Transactions on Neural Networks，2011，22（8）：1256-1267.

[12]Cevikalp H，Larlus D，Douze M，et al.Local subspace classifiers：linear and nonlinear approaches[C]//Proc IEEE Workshop Mach Learn Signal Process，Thessaloniki，Greece，Aug 2007，2007：57-62.

[13]Krinidis S，Chatzis V.A robust fuzzy local information c-meansclustering algorithm[J].IEEE Transactionson Image Processing，2010，19（5）：1328-1337.

[14]Dunn J.A fuzzy relative of the ISODATA process and its use in detecting compact well separated clusters[J].Journal of Cybernetics，1974，3：32-57.

[15]Barth N.The gramian andk-volume inn-space：Some classical results in linear algebra[J].J Young Investigat，1999，2（1）：1-4.

[16]Deza E，Deza M M.Dictionary of distances amsterdam[M].the Netherlands：Elsevier，2006：262-272.

[17]Aster R，Borchers B，Thurber C.Tikhonov regularization[J].Parameter Estimate Inver Probl：Int Geophys，2005，90：89-118.

[18]Cai W，Chen S，Zhang D.Fast and robust fuzzy c-means clustering algorithms incorporating local information for image segmentation[J].Pattern Recognition，2007，40（3）：825-838.

[19]Szilagyi L，Benyo Z，Szilagyii S，et al.MR brain image segmentation using an enhanced fuzzyC-means algorithm[C]//Proceedings of the 25th Annual International Conference of IEEE EMBS，2003：17-21.

[20]赵磊，王斌，张立明.基于模糊C均值聚类和邻域分析的无监督多通道遥感图像变化检测[J].数据采集与处理，2011，26（4）：397-401.