分数阶非线性方程精确解的新方法

闫立梅，刘艳芹

德州学院 数学科学学院，山东 德州 253023

1 引言

目前，分数阶微分方程已经广泛地应用到流体力学、生物医药、固态物理等工程领域[1-4]。寻找分数阶非线性发展方程的解析解或者精确解一直以来是数学工作者的重要研究课题，得到了一些求解分数阶非线性方程的解析和数值方法，其中包括分数阶微分变换法[5-6]，分数阶Adomian分解方法[7]，分数阶同伦扰动法[8-10]，迭代Laplace变换方法[11-12]，分数阶子方程方法[13-14]等。但这些方法大多是求解分数阶非线性方程的近似解，而且存在着各自的缺点。本文将分数阶复变换方法[15]与(G′/G)方法[16]相结合，得到了求解分数阶非线性方程精确解的一种辅助方程新方法，该方法简单有效。文中的分数阶微分算子是Jumarie的修正Riemann-Liouville导数[17]。

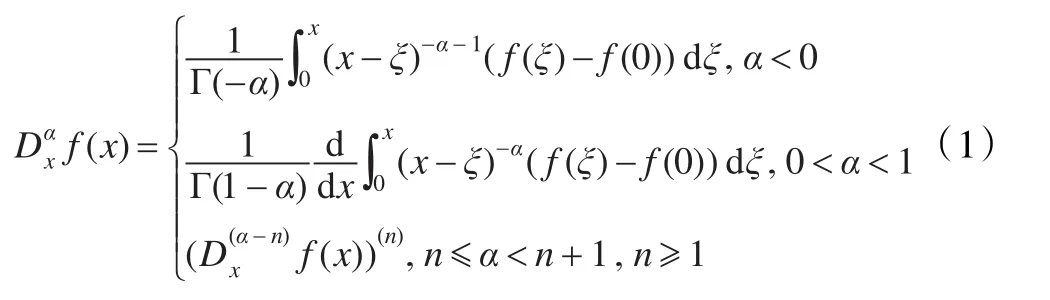
其中，Γ(·)为Gamma函数，定义为：

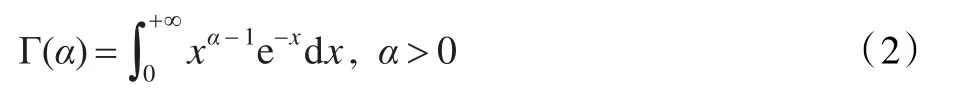
Jumarie的修正Riemann-Liouville导数具有如下性质：

2 方法简介

考虑如下时空分数阶微分方程

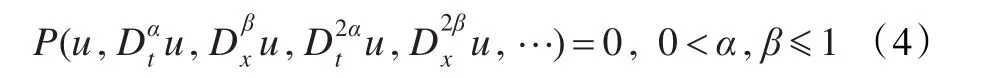
作分数阶复变换：

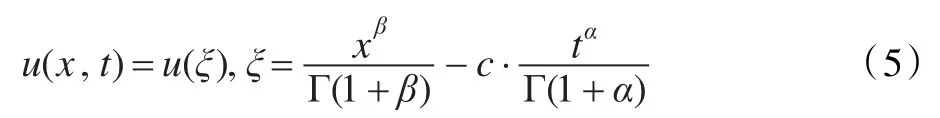
其中c为常数，当α=β=1时式（5）就是通常的行波变换。在式（5）的作用下，式（4）变为：

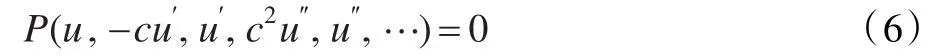
假设式（6）的解u可以表示为G′/G的形式：

其中G=G(ξ)满足方程

am，…，a0是待定的常数，am≠0。正整数m通过式（6）中的最高阶导数项和非线性项来确定。

将式（7）及式（8）带入式（6），比较G′/G的系数，得到一组关于am，…，a0的代数方程，借助于软件Mathematica的符号计算功能及式（8）的解，得到原方程式（4）的解。

式（8）的解如下[16]：

情形1 若λ2-4μ＞0，则

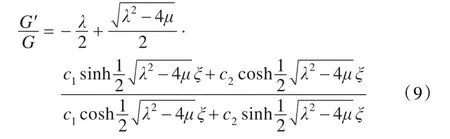
情形2 若λ2-4μ＜0，则

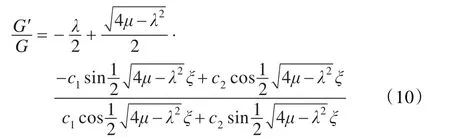
情形3 若λ2-4μ=0，则

3 数值例子

考虑如下时空分数阶Calogero KDV方程：

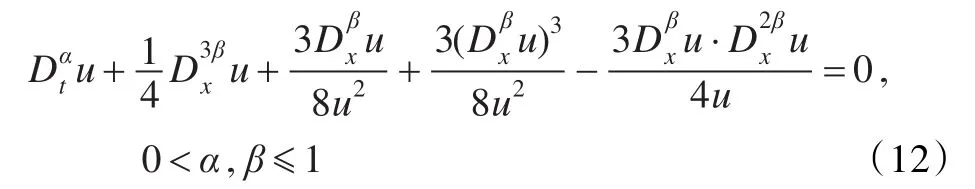
对式（12）作复变换式（5），得到

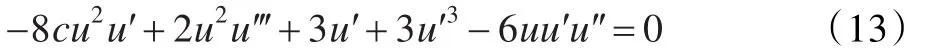
平衡式（13）中的最高阶导数项和非线性项，假设式（13）的解为：

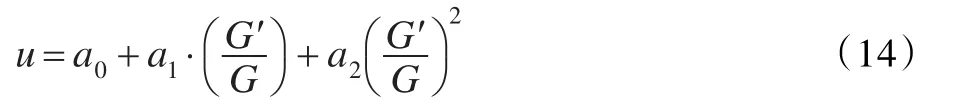
将式（14）及式（8）带入式（13），比较G′/G的系数，得到一组关于a0，a1，a2的方程，借助于 Mathematica的计算功能，得到a0，a1，a2的两组解：

这样，得到时空分数阶Calogero KDV方程各种情形下的解：

（I）

情形1 当λ2-4μ＞0时

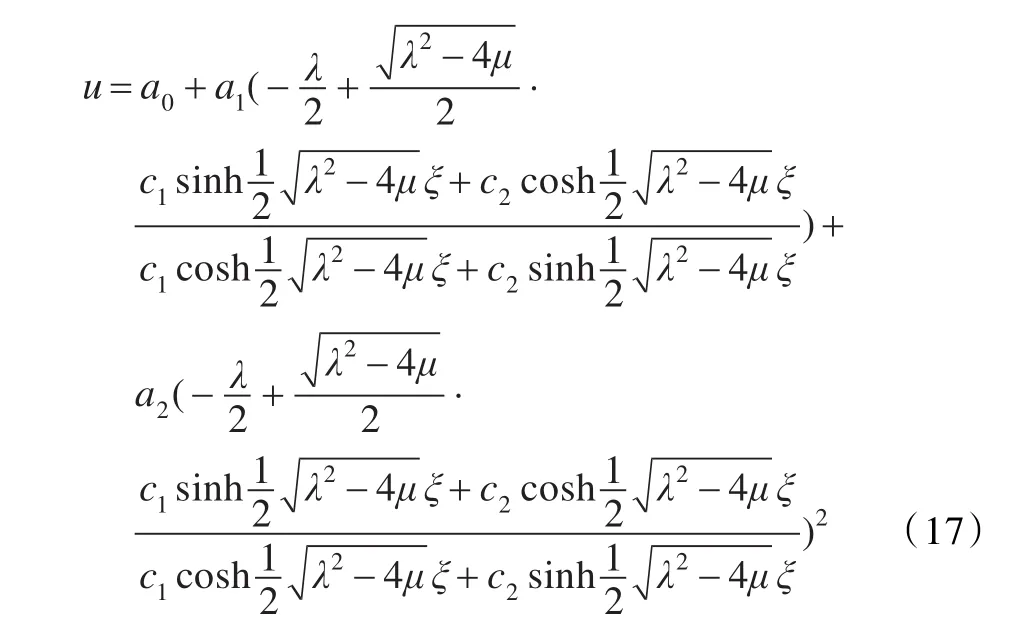
情形2 当λ2-4μ＜0时

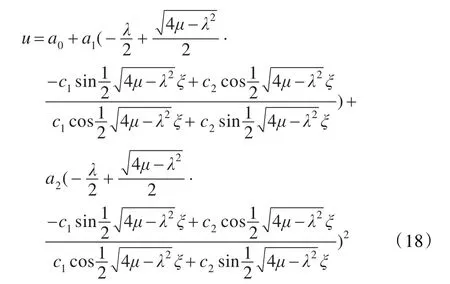
情形3 当λ2-4μ=0时

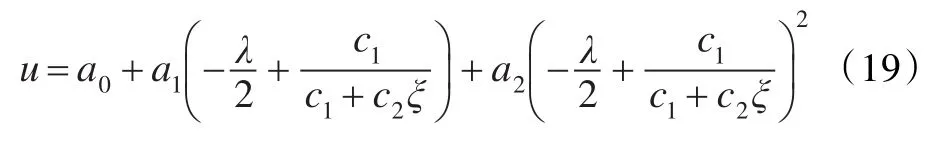
类似地，可以得到（II）时方程（12）的各种解，为简单起见，不再赘述。

4 结果和讨论

将分数阶复变换方法和G′/G方法相结合，得到了求解分数阶非线性方程精确解的一种新方法。当分数阶导数α=β=1时，所得到的精确解就是通常的行波解。数值例子表明，该方法简单有效，能够用来求解一般的分数阶非线性方程。

[1]Sabatier J，Agrawal O P，Tenreiro Machado J A.Advances in fractional calculus：theoretical developments and applications in physics and engineering[M].[S.l.]：Springer，2007.

[2]Baleanu D，Diethelm K，Scalas E，et al.Fractional calculus models and numerical methods in series on complexity，nonlinearity and chaos[C].World Scientific，Singapore，2012.

[3]Liu Y Q，Xin B G.Numerical solutions of a fractional predator-prey system[J].Advances in Difference Equations，2011，190475.

[4]Ma J H，Liu Y Q.Exact solutions for a generalized nonlinear fractional Fokker-Planck equation[J].Nonlinear Analysis：Real World Applications，2010，11（1）：515-521.

[5]Liu J C，Hou G L.Numerical solutions of the space-and time-fractional coupled Burgers equations by generalized differential transform method[J].Applied Mathematics and Computation，2011，217（16）：7001-7008.

[6]Erturk V S，Yildirim A，Momanic S.The differential transform method and Pade approximants for a fractional population growth model[J].International Journal of Numerical Methods for Heat&Fluid Flow，2012，22（6/7）：791-802.

[7]刘艳芹.一类分数阶非线性振子方程的特性研究[J].计算机工程与应用，2012，48（16）：30-32.

[8]He J H.Homotopy perturbation method：a new nonlinear analytical technique[J].Applied Mathematics and Computation，2003，135（1）：73-79.

[9]Yildirim A.Application of the homotopy perturbation method for the Fokker-Planck equation[J].International Journal for Numerical Methods in Biomedical Engineering，2010，26（9）：1144-1154.

[10]刘艳芹.同伦扰动法求解分数阶非线性扩散方程近似解[J].计算机工程与应用，2012，48（6）：28-29.

[11]Jafari H，Nazari M，Baleanu D，et al.A new approach for solving a system of fractional partial differential equations[J].Computers and Mathematics with Applications，2013，66（5）：838-843.

[12]Yan L M.Numerical solutions of fractional Fokker-Planck equations using iterative Laplace transform method[J].Abstract and Applied Analysis，2013，465160.

[13]Liu Y Q，Yan L M.Solutions of fractional Konopelchenko-Dubrovsky and Nizhnik-Novikov-Veselov equations using a generalized fractional sub-equation method[J].Abstract and Applied Analysis，2013，839613.

[14]EI-Sayed A M，Rida S I，Arafa A A.Exact solutions of fractional-order biological population model[J].Communications in Theoretical Physics，2009，52（6）：992-996.

[15]Li Z B，He J H.Fractional complex transform for fractional differential equations[J].Mathematical and Computational Applications，2010，15（5）：970-973.

[16]Wang M L，Li X Z，Zhang J L.TheG′/G-expansion method and travelling wave solutions of nonlinear evolution equations in mathematical physics[J].Physics Letters A，2008，37（4）：417-423.

[17]Jumarie G.Modified riemann—liouville derivative and fractional Taylor series of non-differentiable functions further results[J].Computers and Mathematics with Applications，2006，51（9/10）：1367-1376.