嫦娥三号软着陆轨道设计与控制策略①

成云鹏，张 晔，崔 伟

(中国石油大学(北京)地球物理与信息工程学院，北京102249)

1 问题分析

要保证嫦娥三号在高速飞行的情况下软着陆于预定地区，就要根据已知信息确定嫦娥三号在着陆准备轨道的位置和相应的速度方向和大小，然后确定嫦娥三号软着陆的轨道和不同阶段的控制策略，以实现燃料消耗最少的目的.

可以根据霍曼转移轨道的原理和能量守恒公式求出霍曼转移轨道近月点和远月点的速度.建立坐标系，根据软着陆下降轨迹平面在环月停泊轨道平面内这一结论，建立嫦娥三号的受力方程组，得到近月点和远月点的经纬度，根据位置和速度大小确定速度的方向.

以安全着陆和燃料消耗最少为目标，对软着陆的6 个阶段建立模型计算出最优控制参数，提出控制策略.

2 速度及轨道位置求解

2.1 速度大小

嫦娥三号在被月球引力捕获的过程中需要通过霍曼轨道，设轨道的中心为O 点，初轨道和终轨道没有交点，从初轨转移到终轨需要经过转移轨道，霍曼转移轨道是一个与初轨和终轨相切的椭圆轨道.

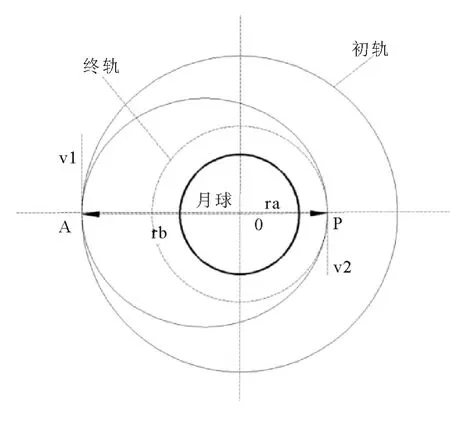
图1 霍曼转移示意图

图2 近月点远月点示意图

在初始轨道上，减速量为Δv1，运行到近地点P时，再次减速，速度减少量为Δv2，卫星将进入终轨运行，从而完成了初轨到终轨的转移.两次速度增量的大小根据初轨和终轨的半径来确定:设初轨半径为ra，终轨半径为rb，μ 为月球引力常数，μ =Gm，G 为万有引力常数，M 为月球质量，初轨轨道速度v 为，计算可得，在远地点圆轨道速度大小为v1=1.633km/s ，近地点圆轨道速度大小为v2=1.673km/s.

根据能量公式可求出转移椭圆轨道近地点P点的速度vp:

霍曼转移所需总的速度增量Δv 为:

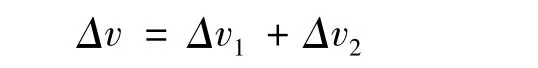
霍曼转移轨道有能量保持守恒:

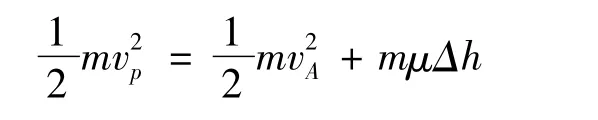
其中Δh 为近月点与远月点的高度差，vA为远月点速度，vp为近月点速度，m 为嫦娥三号的质量，μ 为月球的表面重力加速度，计算可得:vA=1.608km/s.

2.2 近月点与远月点经纬度

月面点及月球引力位都以月固坐标系为参考系.月面点及月球引力位都以月固坐标系为参考系.通过月固坐标系，包含月球自转轴所作的垂直于月球赤道的半平面作为月心经度的起始子午面.从起始子午面沿月球赤道向东量度为月心东经、向西为月心西经，东、西经范围各位0° ～180°.月球的赤道面将月球分为南北半球，与地球类似，月球赤道的月心纬度为0°，南、北纬范围各为0°～90°.

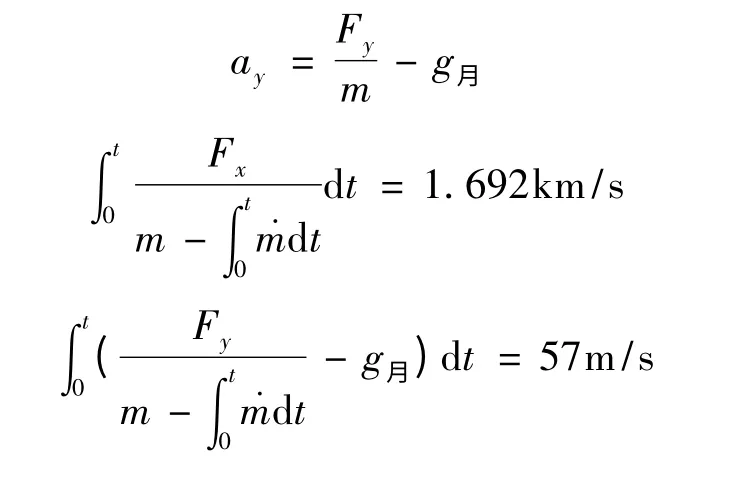
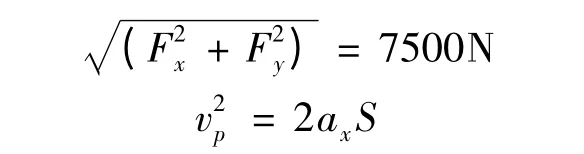
软着陆下降轨迹设计存在一个结论［2］:软着陆下降轨迹平面在环月停泊轨道平面内，即可视为在该软着陆过程中嫦娥三号的经度不变.在主减速过程中假设发动机全力启动，嫦娥三号受到方向改变，与运动轨迹相切的力，建立方程式:经纬度转换公式计算，其中为与着陆点的纬度差，为嫦娥三号在该阶段水平位移，为月球半径.逆推得到近月点的位置为19.51W，28.22N 或19.51W，60.02N，距离月球表面15km.远月点与月球、近月点在同一条直线上，则远月点与近月点纬度为相反数，经度之和为180.得到相应的远月点分别为160.49E，28.22S 或160.49E，60.02S，距离月球表面100km.

根据文献［3］，嫦娥三号到达近月点经度19.0454W，28.9989N，与计算结果19.51W，28.22N 差异不大，可认为计算较为精确.

其中ax为水平方向加速度，ay为竖直方向加速度，Fx为推力的水平方向分力，Fy为推力的竖直方向分力，g月为月球表面重力加速度，t 为主减速阶段时间，S 为嫦娥三号在该阶段水平位移.为燃料消耗的秒耗量，可通过比冲公式得到:F =

其中F 是发动机的推力，单位是牛顿;ve是以米/秒为单位的比冲;˙m 是单位时间燃料消耗的公斤数.

已知着陆点的位置为19.51W，44.12N 可通过

3 六阶段最优控制策略

嫦娥三号着陆过程分为6 个阶段:着陆准备轨道段、主减速段、快速调整段、粗避障段、精避障段、缓速下降阶段.

第一阶段嫦娥三号通过霍曼轨道到达近月点位置进入着陆准备轨道，此时的速度为vp=1.692km/s.该阶段已在前文分析过.

第二阶段主减速阶段是距离月面15km 到3km，通过嫦娥三号的主发动机提供减速动力，发动机产生的力方向始终与运动轨迹相切，此时减速至水平速度57m/s.

第三阶段快速调整段嫦娥三号快速调整姿态，从距月3000m 高空落到距月2400m 高空，水平速度为om/s.此时主发动机竖直朝向月心，主减速发动机的推力竖直向下.

第四阶段粗避障段是距离月面2400m 到100m，通过分析星下光学敏感成像图片，启动姿态调整发动机，粗略避开大陨石坑.

第五阶段精避段是距离月面100m 到30m，分析高分辨率三维高程图，精细避开月面障碍物.

第六阶段缓速下降阶段是距离月面30m 到4m.该阶段的主要任务控制着陆器在距离月面4m处的速度为0m/s，即实现在距离月面4m 处相对月面静止，之后关闭发动机，使嫦娥三号自由落体到落月点.

下面对部分阶段提出有效的控制策略.

3.1 主减速阶段描述

假设不考虑月球自转问题，探测器沿平面轨道运行.建立软着陆坐标系o-x‴y‴z‴，o 为月球卫星近月点在月球表面的投影点，ol为月心，ox‴在当地水平面内指向探测器运动方向oy‴沿着月心ol指向o 点的方向oz‴与ox‴，oy‴构成右手坐标系.该坐标系如下图所示:

图3 软着陆坐标系

1、初始条件:

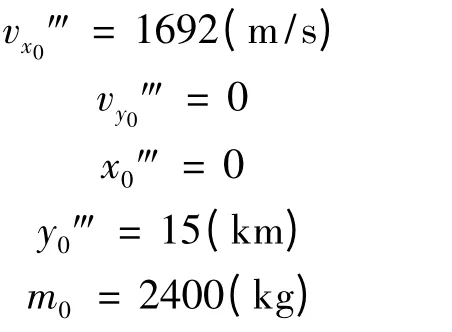
2、终端约束:

3、最佳轨道的终端参数:

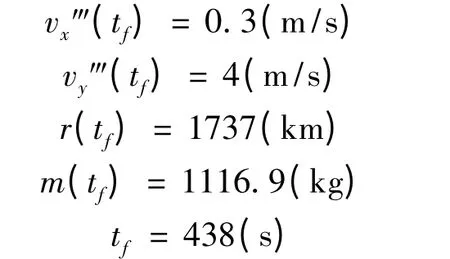
这组参数下的软着陆能量最省轨道为一条一直进行制动的轨道.制动初期基本上沿着速度反向减速，同时有一个向下的制动力分量使探测器的高度减少.制动期间，发动机一直以最大推力进行工作，在它的作用下，探测器的速度方向很快改变，最终垂直于月面.最终结束主减速阶段后嫦娥三号的平行于月球表面的速度为，整个主减速阶段耗时438s.

3.2 基于螺旋前进搜索算法的粗细避障阶段

算法的提出步骤如下:

(1)将给出的2300×2300 的数据矩阵信息保存在指定数组A 内，记为A(i，j)，其中1 ≤i ≤2300，1 ≤j ≤2300，从数据点A(1，1)开始进行地形平坦程度识别.

(2)地形平坦程度识别:选定一个数据点后开始进行顺时针螺旋前进搜索如图4 所示.平坦程度即定义为某点处附近在差值95%范围内点的数目，以A(1，1)为例即A(1，1)附近点海拔在96.9～107.1m 的点数目，这个范围是着陆器所能容忍的最大范围，若超出该值范围，就判断该区域不适合安全着陆.重新定义一个二维数组储存平坦程度值，如:B(1，1)= 6，B(1，2)= 32，B(2，1)=26….

重复(1)(2)步骤完成所有点的识别.由于计算量较大，可以考虑用高斯模糊牺牲一定的精确度来提高计算速度，限于篇幅此处不详述.

图4 螺旋前进搜索算法示意图

图5 距月面100m 处的数字高程图

通过对距月面100m 处的数字高程图中所有数据矩阵进行高斯模糊，模糊个别凸起奇异点对结果的影响，均匀系统抽样运用顺时针螺旋前进搜索避障算法，分析得到像素点为最佳着落点A(287，353).

3.3 其他阶段概述

快速调整段:

嫦娥三号快速调整选择显式制导方法不能对姿态角的终值进行控制，但是，软着陆需要着陆器以垂直姿态着陆到月面.因此在动力下降段结束后，需要马上进行姿态调整.从燃耗的角度看，姿态调整的时间越短越好，然而太短的时间也会使终端角度误差变大.这里，要求在10s 之内完成.在短时间之内，如果仅用反馈控制器完成大角度机动比较困难，因此有必要加上一个前馈控制器来加速收敛过程.

缓速下降阶段:

缓速下降阶段主要考虑着陆的安全性，为了保证月面的速度和姿态控制精度，尽可能以较小的设定速度匀减速垂直下降，消除水平速度和加速度，直到收到关机敏感器信号.考虑到推进剂的消耗和导航位置漂移，选择下降速度为－2m/s.缓速下降段制导律与悬停段制导律结构形式一样，区别在于制导参数不同.水平方向目标速度为0m/s，位置控制目标为进入缓速下降段初始时刻的着陆位置.垂直方向，高度20m 以上控制速度和加速度;高度低于20 米，只控制加速度且指令加速度稍小于当地月球引力加速度，以提高着陆器安全下降的可靠性.

4 总 结

本文根据霍曼转移轨道的原理和能量守恒公式计算出嫦娥三号在近远月点的速度.建立坐标系，求出近远月点的经纬度，从而确定了嫦娥三号的着陆准备轨道.之后对软着陆的六个控制阶段给出了一些最优控制策略.在主减速阶段通过构造约束条件确定最优控制参数.快速调整阶段给卫星添加一个前馈控制器来实现快速调整姿态以节省燃料.粗避障阶段用螺旋前进搜索算法，向外识别平坦度寻找最佳着陆区.同时运用高斯模糊算法减小计算量.

本文中方法的计算结果与实际结果比较接近，精确给出了着陆准备轨道.对六个阶段的给出了一些最优控制策略.但同时模型中存在许多假设和简化，没有考虑较为复杂的摄动，月球的自转等，对于航天航空精细控制的应用上有所欠缺.

［1］ 胡其正，杨芳《宇航概论》［M］.北京:中国科学技术出版社，2010:101－102.

［2］ 王鹏基，张熇，曲广吉.月球软着陆飞行动力学和制导控制建模与仿真［J］.中国科学(E 辑:技术科学)，2009，03:521－527.

［3］ 张洪华，关轶峰，黄翔宇，李骥，赵宇，于萍，张晓文，杨巍，梁俊，王大轶.嫦娥三号着陆器动力下降的制导导航与控制［J］.中国科学:技术科学，2014，04:377－384.

［4］ 张洪华，梁俊，黄翔宇，赵宇，王立，关轶峰，程铭，李骥，王鹏基，于洁，袁利.嫦娥三号自主避障软着陆控制技术［J］.中国科学:技术科学，2014，06:559－568.

［5］ 丁怡心，廖勇毅，高斯模糊算法优化及实现［J］.现代计算机(专业版)，2010，08:76－77+100.

［6］ 郗晓宁《月球探测器轨道设计》［M］.长沙:国防工业出版社，2001.