一种有灰色初值函数的泛函微分方程数据预测①

刘雅静

(华东理工大学商学院，上海200237)

0 引 言

经济指标的准确预测是国家对宏观经济正确调控的必要前提，对掌控经济运行态势、为正确的经济决策提供依据都十分重要.但经济预测又是困难的，实际的经济数据往往变化多端，并且经济系统是非常复杂的系统［1］.其中广泛存在着非线性时变性和不确定作用关系，各种宏观经济模型大部分都是线性模型，线性模型在发挥巨大作用的同时也存在缺陷，即很难把握宏观经济系统中的非线性现象，这必然导致结果上的误差加大［2］.经济学界的工作者们因此对各种线性模型做了大量改进工作，但结果往往并不理想，迫使人们寻求一些非线性工具进行宏观经济建模［3］，因而经济预测方法非常多.即便如此，往往实际的经济数据仍难以简单地以某单一方法来预测.另外，很多经济数据之间的联系不能很好地体现出来，需要深入到数据的内部去寻找.而这需要对数据做理论推算处理，这也是困难的工作.

灰色系统理论是研究解决灰色系统分析、建模、预测、决策和控制的理论.灰色预测模型具有所需样本数据少，运算简便等特点［4］.自从灰色理论创立以来，在许多领域都有着比较广泛的应用［5～8］.本文将以一个经济预测实例作为例子，根据这个实际例子的特点，提出的一个较好的预测方法.该方法引入中立型泛函微分方程，将泛函微分方程与灰色GM(1，1)模型结合来进行预测.并通过差商计算，从理论上推算出使用泛函微分方程与灰色GM(1，1)模型结合进行预测的理论依据.

1 预备知识

(1)灰色GM(1，1)模型的概念

对时间序列{x(0)(t)}(t=1，2，…，N)，做其1阶累加序列N).对累加序列{x(1)(t)}建立GM(1，1)模型:可得指数曲线:x(1)(t)=将预测序列}还原为原序列{x(0)(t)}即得预测曲线.

(2)中立型泛函微分方程的概念

给出具有如下形式的方程:

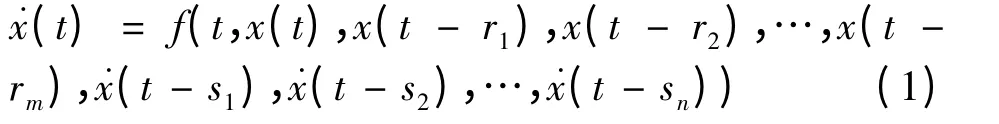
(1)式中，ri≥0(i=1，2，…，m)，si＞0(i=1，2，…，n).D 为Rn中的一个开集，

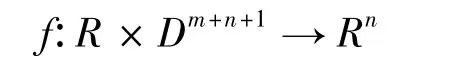
称方程(1)为中立型泛函微分方程.

2 泛函微分方程预测

某市要根据该市近年来的第三产业产值数据对该市第三产业发展情况进行预测，首先需要根据实际产值数据建立合理的预测系统模型.该市多年的第三产业产值数据见表1，表1 中的序号表示年份.

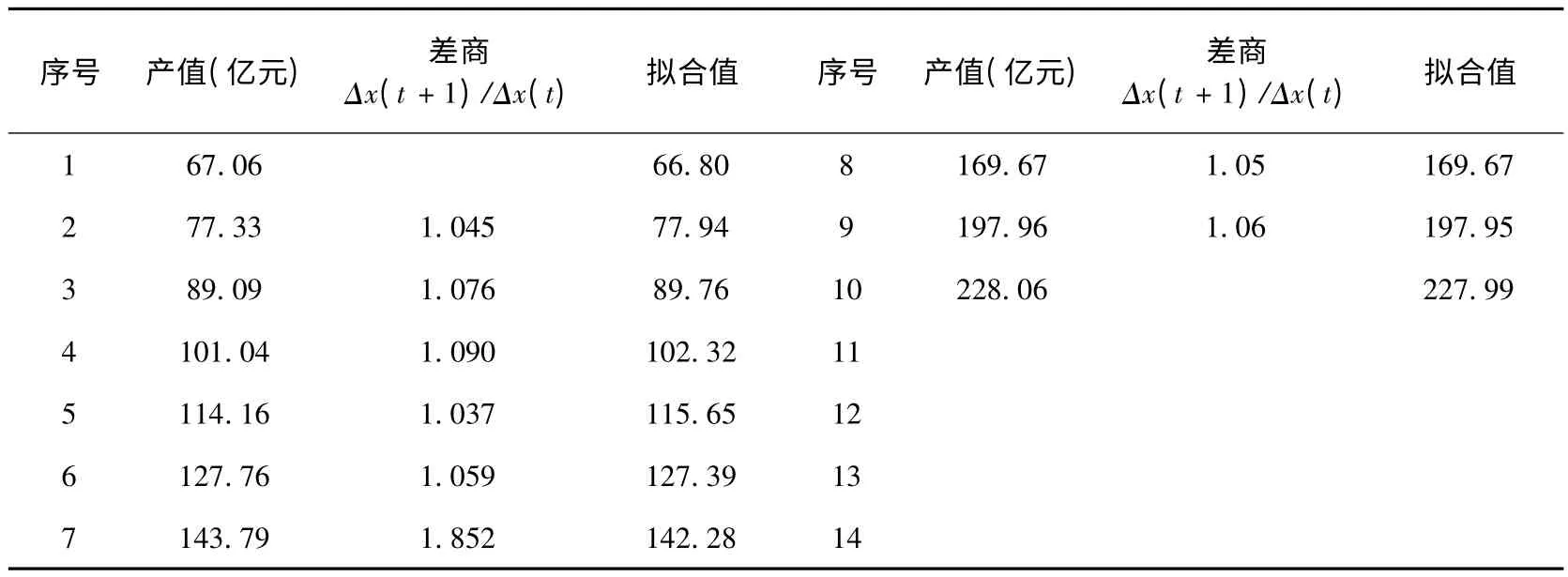
表1 第三产业逐年产值表

由表1 可知，该市第三产业产值数据发展变化的大致曲线为:从序号1 到序号7 处为平滑曲线，产值数据单调上升;在序号7 和序号8 之间产值数据有一突变，之后产值数据又平稳地单调上升.

对实际的第三产业产值数据做差商.从序号1到序号7 数据的差商Δx(t+1)/Δx(t)的期望值为1.06，而从序号8 到序号10 的数据的差商也近似等于1.06，而序号7 到序号8 的数据的差商有一突变，为1.852.由于有

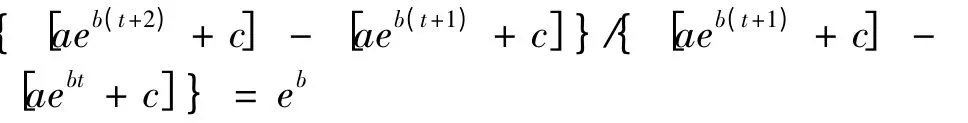
所以序号1 到序号7 的产值数据可用灰色GM(1，1)模型拟合.

经计算，拟合曲线为

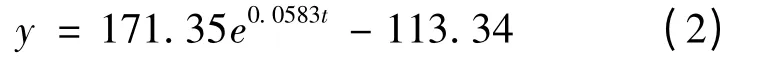
用公式(2)算出的拟合值列入表1 中.

由于从序号7 到序号8 的差商有一突变，因此不能对序号8 到序号10 的第三产业产值数据一并利用公式(2)进行拟合，需要找出序号8 到序号10的产值数据与序号1 到序号7 的产值数据之间的内在联系.经计算，有关系

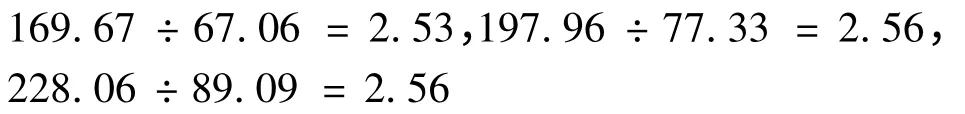
又因序号8 到序号10 的数据差商约为常数1.06，而序号1 到序号7 的数据差商的期望值也约为1.06，所以序号8 到序号10 的数据与序号1 到序号7 的数据之间应有如下泛函微分方程关系

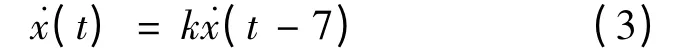
于是，可用公式(2)作为方程(3)的初始函数.解方程(3)，得

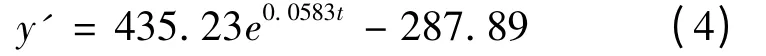
公式(4)即为得到的预测系统模型.

利用公式(4)对序号11 到序号14 的第三产业产值进行预测.预测结果列入表2 中.

表2 预测结果表

11 259.41 259.89 0.48 12 292.41 293.75 1.34 13 327.18 323.56 3.62 14 362.39 361.39 1.00

表2 中，将序号10 以后4 年的实际第三产业产值数据也填入表2 中，经和利用公式(4)得出的预测值比较，误差很小，说明预测系统模型合理，预测结果有效.

3 结 语

本文提出了一种以灰色模型拟合曲线为初值函数，以中立型泛函微分方程的解为预测函数的预测方法.该方法需以对数据的理论证明为根据，因而这一方法有良好的预测效果.对实例的预测结果、拟合精度也说明了这一预测方法效果良好，有实用价值.

［1］ 邓聚龙.灰色预测与决策［M］.武汉:华中理工大学出版社，1986.

［2］ 刘思峰，党耀国，方志耕，等.灰色系统理论及其应用［M］.北京:科学出版社，2010.

［3］ 石为人，冯治恒.基于灰色理论与BP 算法的宏观经济预测模型研究［J］.计算机与数字工程，2007，35(1):8－10.

［4］ DENG J L.Introduction to Grey System Theory［J］.Journal of Grey System，1989，1(01):1－24.

［5］ 吴天魁，王波，顾基发.基于最小二乘法的改进GM(1，1)模型在上海市社会总抚养比预测中的应用［J］.系统科学与数学，2015，35(1):75－84.

［6］ 张彬，西桂权.基于背景值和边值修正的GM(1，1)模型优化［J］.系统工程理论与实践，2013，33(3):682－688.

［7］ 赵爱文，李东.中国碳排放灰色预测［J］.数学的实践与认识，2012，42(4):61－70.

［8］ 吴天魁，王波，周晓辉，等.火灾损失预测的改进GM(1，1)模型［J］.数学理论与应用，2014，34(1):58－70.