一种基于约束框架的棱柱网格生成方法

孙 岩，邓小刚，王光学，毛枚良，张玉伦

(1.中国空气动力研究与发展中心空气动力学国家重点实验室，四川绵阳 621000; 2.国防科学技术大学计算机学院，湖南长沙 410073)

一种基于约束框架的棱柱网格生成方法

孙 岩1，*，邓小刚2，王光学1，毛枚良1，张玉伦1

(1.中国空气动力研究与发展中心空气动力学国家重点实验室，四川绵阳 621000; 2.国防科学技术大学计算机学院，湖南长沙 410073)

提出了一种基于约束框架的棱柱网格生成方法，即利用物面网格节点与背景结构框架网格之间的单一映射关系线性插值生成棱柱网格。背景结构框架网格基于TFI方法生成。物面网格节点与背景框架网格之间的映射关系通过一种线性投影方法建立。然后通过V型槽、圆球、M6机翼和F6翼身组合体四种不同外形对该棱柱网格生成方法进行了测试，测试结果表明该方法能够避免棱柱网格生成中的网格交叉现象，保证棱柱网格的成功生成。该方法在棱柱网格质量控制、棱柱网格局部修改等方面具有较好的效率和优势，但背景框架网格的生成依然是该方法的一个瓶颈，需要进一步的研究。

约束框架;TFI;背景结构网格;棱柱网格生成;映射

0 引 言

高质量的离散网格是获得准确CFD计算结果的基础。目前，尽管出现了一些高效的商业网格划分软件，如Gridgen、ICEMCFD等，但网格生成依然占有约60%的CFD工作量。高效、高质量的网格全自动划分仍然是CFD应用面临的关键研究问题之一［1-2］。

三角形或四面体网格可以对任意二维或三维区域进行自动填充，实现任意复杂外形网格的全自动生成，但在模拟高雷诺数边界层流动时显得力不从心。全六面体流场结构网格可以在边界层区域生成较大长细比的网格，具有较好的模拟精度且内存占用小，但复杂外形的空间拓扑设计和网格节点分布的精细调整极大地增加了全六面体结构网格生成的难度和时间消耗。棱柱网格具有非结构网格和结构网格的双重性质，属于半结构网格类型，采用棱柱网格可以比较好地模拟边界层内的高梯度流动，因此，在流场边界层区域采用棱柱网格，在流动变化缓慢的区域采用四面体网格或笛卡尔网格的混合网格方法受到了很多CFD研究者的青睐［2-5］。

目前，棱柱网格生成方法主要有三类:法矢推进［6-10］、各向异性四面体网格聚合［11-12］和Level set界面追踪方法［13-15］。法矢推进生成棱柱网格的思路最早由Nakahashi［6-7］和Steger［8］提出，他们的方法是通过沿着物面法向一步一步推进生成棱柱网格，但在物面法矢存在奇性的位置需要进行特殊的处理，后续研究工作对他们的方法进行了诸多的改进［9-10］，以提高方法的鲁棒性和自动化程度。各向异性四面体网格聚合方法首先通过Advancing Layer方法自动生成各向异性四面体网格，然后基于一定的判定准则对网格单元进行聚合，从而得到壁面附近的棱柱网格单元，该方法具有很好的自动化程度，但聚合后的网格往往存在少数网格质量很差无法聚合的四面体单元，影响整体的计算效率和计算精度。基于Level set的方法是近些年快速发展的混合网格方法，其中具有代表性的是Dawns［13-14］发展的基于Level set的棱柱/笛卡尔混合网格生成方法，能够自动实现极端复杂外形下混合网格的快速生成，但该方法要求物面网格和笛卡尔背景网格具有相近的网格尺寸以避免扭曲网格的产生［15］。

本文借鉴文献［16］提出的背景网格思路，提出一种基于约束框架的棱柱网格生成方法，即在物面外形周围利用TFI(Transfinite Interpolation)方法生成一层粗的背景结构网格，通过背景结构网格与物面网格节点之间的映射关系插值得到棱柱网格的节点坐标，实现棱柱网格的高效、高质量生成。

1 方法描述

基于约束框架生成棱柱网格方法的主要思想是:在物面外形周围利用TFI超限插值方法生成较粗的背景结构网格，然后利用物面网格节点与背景结构网格之间的映射关系插值得到棱柱网格。基于弧长分布的TFI方法见文献［17］。

图1为基于约束框架的棱柱网格生成方法示意图。其中，红色的背景结构网格将物面边界层区域分割成多个六面体框架，将物面分割成多个四边形框架，构成控制棱柱网格生成的约束框架。蓝色的点表示物面网格的节点Node，对于任一物面网格节点N1S，可以寻找到距离节点最近的物面框架四边形，从而建立起物面网格节点与物面框架四边形之间的映射关系。棱柱网格每一层的节点坐标，利用映射系数和节点对应的当前层约束框架四边形节点的坐标插值得到，详细的计算方法见下文。

图1 棱柱网格生成方法示意图Fig.1 Sketch of prismatic grid generation method

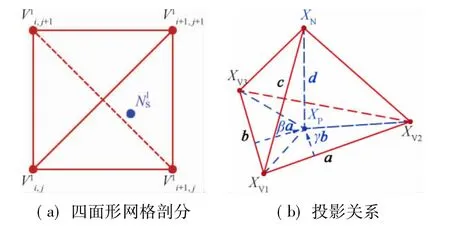
图2 四边形网格剖分与投影关系Fig.2 Splitting method of rectangle grid and projection relation

图2中a、b、c为网格节点定义的矢量，d为物面节点XN在物面框架三角形组成的平面V1V2V3上的投影点XP到节点XN的矢量，所以有:

XP位于平面V1V2V3上，所以XP可以表示为:

利用式(1)、式(2)、式(5)，可得:

所以投影点坐标XP可以表示为三个点的线性叠加:

其中α=1－β－γ。由式(3)、式(4)、式(5)可得:

利用a和b与d垂直的关系，结合式(8)，可以计算出:

α、β、γ均位于区间［0，1］之间时，表面投影点位于三角形内部，其它则表明投影点位于三角形外部。对于凸曲面外形，物面网格节点的投影点可能不位于任一四边形剖分的三角形内部，这种情况通常出现在曲面边界不光滑过渡区域。为了建立起映射关系，可以采用二次过滤的方法，首先建立投影点位于三角形内部的物面网格节点与背景框架之间的映射关系，对于投影点不位于三角形内部的物面网格节点，给定一个容差σ，α、β、γ在区间［-σ，1+σ］之间，认为投影点位于三角形内部，再利用距离最小准则搜索出与之映射的物面框架四边形。

所以，

对于曲面外形，物面网格节点通常不位于三角形所在的平面上，即d=|d|≠0，在计算棱柱网格节点坐标时，需要修正偏移距离d的影响，否则当第一层网格厚度非常小时，容易造成网格交叉出现负体积，导致网格生成失败。定义三角形平面单位法向矢量d0:

所以有:

ε的绝对值定义了物面网格节点到物面框架三角形的距离，ε的符号定义了物面网格节点相对物面框架三角形平面的位置。ε＞0，物面网格节点位于平面法向一侧;ε＜0，物面网格节点位于平面法向反向一侧;ε=0，物面网格节点位于平面上。ε定义了修正距离的大小和方向，其值可以通过下式计算得到。

在计算棱柱网格每一层节点坐标时，保持插值系数α、β、γ和ε不变，利用节点对应当前层约束框架节点坐标插值得到新的棱柱网格节点坐标，如式(14)。

其中，

上标i表示第i层网格节点。

2 网格生成实例

通过4种典型外形的棱柱网格生成实例，验证本文提出方法的可行性，4种外形分别是V型槽、圆球、M6机翼和F6翼身组合体。

2.1 V型槽

V型槽是验证棱柱网格生成方法的一个常用算例，构成V型槽的两个平面的法矢在空间上是交叉的，在利用推进方法生成棱柱网格时，如果推进步长过大，会造成网格交叉出现负体积，导致网格生成失败。图3(a)为V型槽的表面三角网格划分和采用的框架边线，为了体现框架对棱柱网格生成的约束效果，空间框架边线采用弧线，将棱柱网格最外层网格面约束在一个光滑弧形曲面上。图3(b)为棱柱网格生长的剖面视图，可以看出，在槽底的棱柱网格的生长不是沿着平面的法向推进，而是在框架的约束下以与法向一定的倾斜角度生长，从而保证了网格之间的不交叉，网格的生长速率也由框架沿棱柱网格生成方向的边线上的节点分布控制，保证了统一的增长速率和每一层棱柱网格面的光滑性。图3(c)～图3(f)为基于同一约束框架的不同表面网格密度的V型槽棱柱网格的生成。可以看出:网格密度的变化，对棱柱网格最外层网格面外形的影响很小。

2.2 圆球

圆球面为外凸面，外法矢是发散的，在空间上不交叉，是法向推进方法最理想的外形。采用圆球作为验证算例，一方面因为球面会使得表面网格节点和物面框架之间存在距离，需要进行距离修正，另一方面是为了体现本文方法对棱柱网格的雕塑作用，将圆球棱柱网格的最外层外形约束在一个椭球面上。图4(a)为圆球表面网格分布和约束框架外形，约束框架的外表面被投影到一个椭球面上。图4(b)为圆球棱柱网格的剖面视图，从图中可以看出，通过距离修正，球面外形被一层层传递到棱柱网格层中，随着离球面距离的增大，距离修正量的影响变小，最外层的外形受距离修正影响比较小，保持为椭球形状。图4(c)～图4(f)为基于同一组约束框架的不同表面网格密度的球体棱柱网格生成，可以看出:随着网格密度的增加，棱柱网格最外层面外形均保持为椭球形状，并且网格密度越大，最外层网格面越光滑。

图3 V型槽棱柱网格生成Fig.3 Prismatic grid generation for V-shaped groove

图4 圆球棱柱网格生成Fig.4 Prismatic grid generation for sphere

2.3 M6机翼

M6机翼是CFD验证计算中经常使用的一个模型，它是一个后掠机翼，机翼后缘具有一个很小的厚度，外形与表面网格如图5(a)。图5(b)为M6机翼棱柱网格生成采用的约束框架，在靠近机翼前缘、后缘和翼梢位置分别增加了控制边线，以提高约束框架与机翼物面之间的正交性，提高棱柱网格生成的质量。图5(c)～图5(d)分别为翼根和翼梢位置生成的棱柱网格的剖视图，可以看出:棱柱网格在框架约束下沿着各自的方向增长，相互之间没有交叉，保证了棱柱网格体积非负。图5(e)～图5(f)分别为翼梢前缘和翼梢后缘棱柱网格最外层网格面形状，可以看出:棱柱网格最外层网格面形状受到了框架的约束，呈现出规则的形状;翼梢后缘和机翼后缘采用四边形网格生成四棱柱网格，是为了避免采用三角形网格在棱柱网格生成过程中三角形被过度拉伸导致网格质量太差。

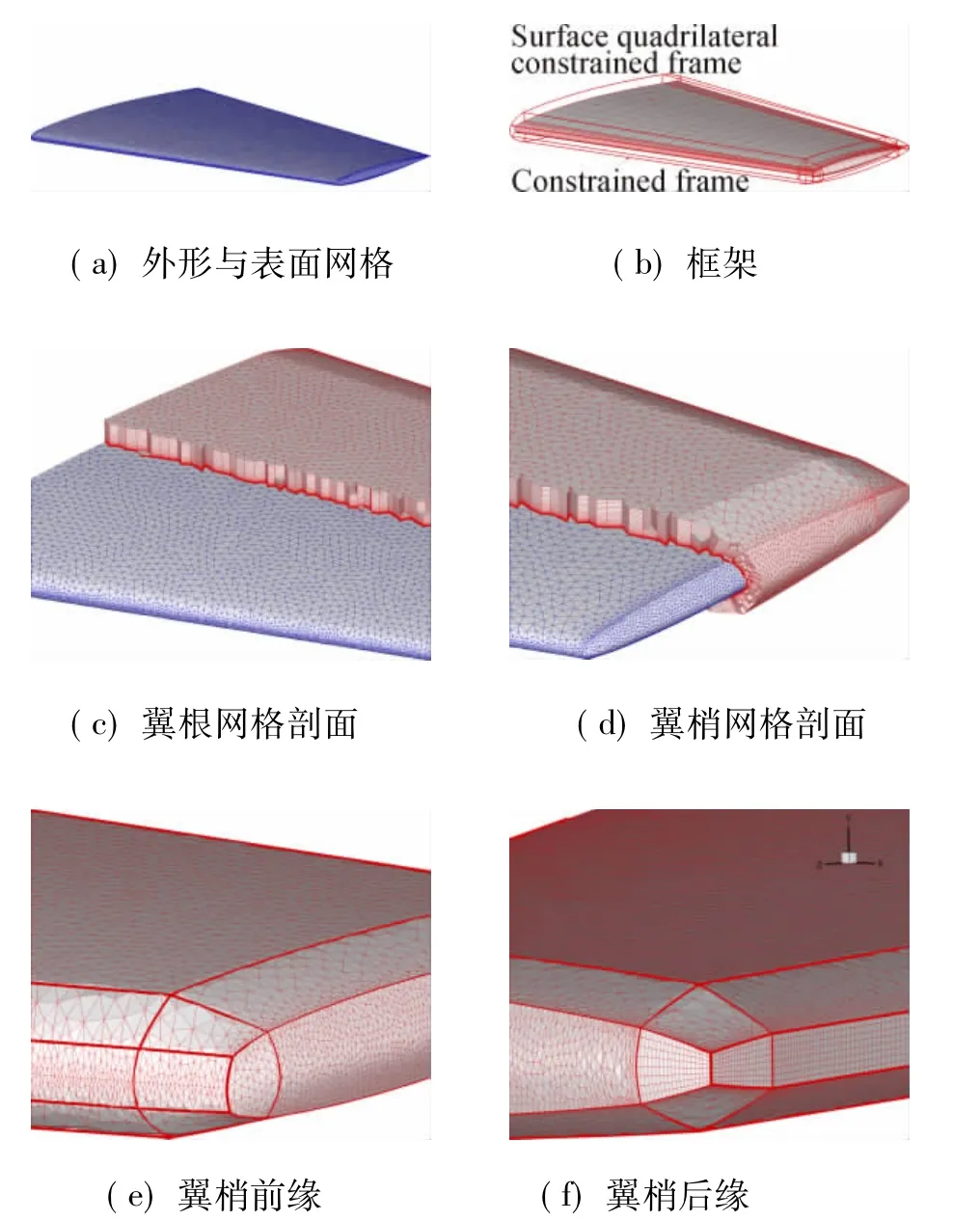
图5 M6机翼棱柱网格生成Fig.5 Prismatic grid generation for M6 wing

2.4 F6翼身组合体

F6翼身组合体是第二届、第三届AIAA阻力预测会议选用的模型，F6翼身组合体外形与表面网格如图6(a)，表面网格在机翼翼梢、机翼后缘及机身与后缘连接位置采用四边形网格，以避免这些位置采用三角形网格导致网格被过度拉伸造成网格质量太差。图6(b)为F6模型棱柱网格生成采用约束框架，约束框架在模型几何变化明显的区域增加了控制边线，以提高框架和模型表面的正交性，提高棱柱网格生成的质量。图6(c)～图6(d)分别为翼身连接位置棱柱网格和翼梢位置网格的剖视图，可以看出:棱柱网格生长良好，没有出现交叉现象。图6(e)～图6(f)为翼梢后缘和翼根后缘位置棱柱网格最外层网格面形状，由于在这些位置的表面网格中采用了四边形网格，有效提高了棱柱网格的生成质量。

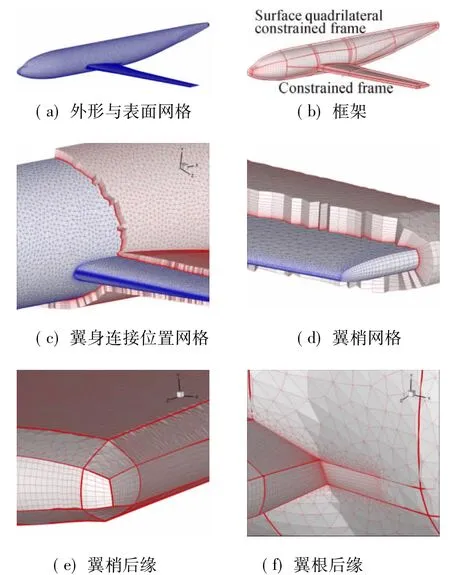
图6 F6翼身组合体棱柱网格生成Fig.6 Prismatic grid generation for F6 wing-body

3 进一步讨论

前一节通过四种外形网格生成实例验证了本文提出方法的可行性，本节将针对该方法的优缺点开展进一步的讨论。

首先，与法向推进生成棱柱网格方法相比，本文提出的基于约束框架的棱柱网格生成方法需要生成背景结构网格框架，增加了棱柱网格生成的工作量。但同生成全六面体流场结构网格不同，本文生成的背景结构网格首先不用考虑复杂的空间拓扑，只需要将物面四边形边线沿着物面法向推进生成空间边线;其次背景结构网格的节点分布不需要考虑网格尺寸之间的连续性，不需要调整网格节点分布，对于绝大多数外形，只需均匀分布框架边线上的节点。上述两点均是全六面体流场结构网格生成中需要考虑且最费时的，本文方法均不用考虑，极大地降低了背景结构网格框架生成的难度和时间消耗。当然，目前背景结构网格框架的生成还是需要一定的人工参与，如何实现背景结构网格的自动生成还需要进一步地研究。

其次，同法向推进生成棱柱网格方法相比，本文方法牺牲了部分法矢交叉位置棱柱网格的壁面正交性来避免网格生成过程中的交叉现象，保证棱柱网格生成的成功。法向推进方法在法矢交叉位置，通过减小推进步长避免网格出现交叉，不同推进步长使得生成的网格面不光滑，导致网格质量降低，因此需要通过光滑算法对新生成的网格面进行光滑。基于约束框架的方法，不仅可以保证统一的网格增长速率，还可以将每一层棱柱网格面约束成比较光滑的形状，对于棱柱生长方向偏离法矢方向的位置，通过增加控制线，可以将偏离程度和偏离区域控制在最小，保证大部分棱柱网格具有较高的质量。

此外，基于约束框架生成棱柱网格的方法具有的一个特点是，当物面表面网格发生变动时，只需要在网格密度变化可能造成棱柱网格质量降低的区域调整背景结构网格框架及调整法向边线的节点分布，然后从新计算网格节点在物面框架上的映射系数，最后插值计算得到全新的棱柱网格。在开展网格收敛性研究时，该方法不仅可以有效提高网格生成的效率，还可提高棱柱网格之间的几何相似性，对于改善网格收敛性研究的精度具有重要的参考价值。

最后，该方法生成棱柱网格具有很高的效率。如上节中的F6翼身组合体模型，物面网格有57 763个节点，108 572个三角形单元，3 136个四边形单元，物面框架被分成5 500个四边形区域，采用3.0G的AMD处理器仅需7.08 s即可生成20层的棱柱网格。棱柱网格生成的主要时间消耗是建立物面网格节点与物面框架之间的映射关系，本文采用遍历循环的方式，如果采用高效的数据结构和搜索算法，该方法的效率还将有很大的提高。

4 结 论

本文提出了一种基于约束框架的棱柱网格生成方法，通过生成粗的背景结构网格框架控制棱柱网格节点的生长方向和生长速率，并通过四种不同外形对该方法进行了测试，可以得到以下结论:

(1)通过建立表面网格点和背景框架网格之间的映射关系，避免了棱柱网格生成过程中的网格交叉现象，保证了棱柱网格的成功生成。

(2)该方法直接对表面网格点的生长速率和生长方向进行控制，不依赖于表面网格的拓扑类型，能够应用于混合型棱柱网格的生成(如F6算例中翼稍附近的四边形网格和周围的三角形网格)，具有一定的普适性。

(3)背景框架网格可以控制棱柱网格的生长区域，通过添加控制线减小网格挤压区域的影响范围，保证大部分区域的网格质量。

(4)物面网格发生改变(如网格加密或网格局部修改)时，仅需要对背景网格框架进行局部的修改，即可快速生成新的棱柱网格，能够大幅降低棱柱网格修改的时间消耗。

［1］ Thompson J F，Soni B K.Handbook of grid generation［M］.New York:Chemical Rubber Company Press，1998.

［2］ Aaron K，Venkateswaran S.High aspect ratio grid effects on the accuracy of Navier-Stokes solutions on unstructured meshes［J］.Computers＆Fluids，2012，65:66-79.

［3］ Kallinderis Y，Khawaja A Mcmorris H.Hybrid prismatic/tetrahedral grid generation for complex geometries［R］.AIAA 95-0211，1995.

［4］ Sharov D，Nakahashi K.Hybrid prismatic/tetrahedral grid generation for viscous flow applications［R］.AIAA 96-2000，1996.

［5］ Deister F，Hirschel E H.Adaptive cartesian/prism grid generation and solutions for arbitrary geometries［R］.AIAA 99-16631，1999.

［6］ Nakahashi K.A finite-element method on prismatic elements for the three-dimensional navier-stokes equations［C］//11thInternational Conference on Numerical Methods in Fluid Dynamics:Lecture Notes in Physics(No.323).Berrin:Springer-Verlag，1988:434-438.

［7］ Nakahashi K.Marching grid generation for external viscous flow problems［J］.Transactions of the Japan Society for Aeronautical and Space Science，1992，35:88-102.

［8］ Steger J L.Grid generation with hyperbolic partial differential equations for application to complex configurations［M］//Numerical Grid Generation in Computational Fluid Dynamics and Related Fields.New York:North Holland Press，1991:871-886.

［9］ Matsuno K.Hyperbolic upwind method for prismatic grid generation［R］.AIAA 2000-1003.

［10］Garimella R V，Shephard M S.Boundary layer mesh generation for viscous flow simulations［J］.International Journal for Numerical Methods in Engineering，2000，49:193-218.

［11］Zhao Zhong，Zhang Laiping，He Xin.Hybrid grid generation technique for complex geometries based on agglomeration of anisotropic tetrahedrons［J］.Acta Aerodynamica Sinica，2013，31(3):34-39.(in Chinese)

赵钟，张来平，赫新.基于“各向异性”四面体网格聚合的复杂外形混合网格生成方法［J］.空气动力学学报，2013，31(3): 34-39.

［12］Zhang Laiping，Zhao Zhong，Chang Xinghua，et al.A 3D hybrid grid generation technique and a multigrid/parallel algorithm based on anisotropic agglomeration approach［J］.Chinese Journal of Aeronautics，2013，26(1):47-62.

［13］Dawes W N，Harvey S A，Fellows S，et al.Viscous layer meshes from level sets on Cartesian meshes［R］.AIAA Paper 200-0555，2007.

［14］Dawes W N，Harvey S A，Fellows S，et al.A practical demonstration of scalable parallel mesh generation［R］.AIAA 2009-0981.

［15］Park S，Jeong B，Lee J G，et al.Hybrid grid generation for viscous flow analysis［J］.International Journal for Numerical Methods in Fluids，2013，71:891-909.

［16］Liu Xueqiang，Qin Ning，Xia Hao.Fast dynamic grid deformation based on delaunay graph mapping［J］.Journal of Computational Physics，2006，211:405-423.

［17］Soni B K.Two and three dimensional grid generation for internal flow applications of computational fluid dynamics［R］.AIAA 85-1526，1985.

A prismatic grid generation method based on constrained frame

Sun Yan1，*，Deng Xiaogang2，Wang Guangxue1，Mao Meiliang1，Zhang Yulun1
(1.State Key Laboratory of Aerodynamics，China Aerodynamics Research and Development Center，Mianyang Sichuan 621000，China; 2.School of Computer Science，National University of Defense Technology，Changsha 410073，China)

A prismatic grid generation method based on constrained frame is presented.The prismatic grid is generated by linear interpolation using one to one mapping between surface grid nodes and background structured grid frame.The background frame is generated by TFI method.The one to one mapping is established using a linear projection method.Then，the prismatic grid generation method is tested through four different shape cases:V-shape groove，sphere，M6 wing and F6 wing-body.The test results show that this method can avoid overlapped cells and make prismatic grid generation successful.Finally，discussion about advantages and disadvantages of the present method shows that this method functionates better on quality control and local modification of prismatic grid，but the generation of background grid frame is still a bottleneck and need further investigation.

constrained frame;Transfinite Interpolation;background structured grid;prismatic grid generation;mapping

V211.3

A

10.7638/kqdlxxb-2013.0003

0258-1825(2015)03-0319-06

2013-01-16;

2013-03-08

国家重点基础研究发展计划(2014CB744803);国家863项目(2012AA051304)

孙岩*(1986-)，男，安徽凤阳人，博士研究生，助理研究员，研究方向:计算流体力学.E-mail:supersunyan@163.com

孙岩，邓小刚，王光学，等.一种基于约束框架的棱柱网格生成方法［J］.空气动力学学报，2015，33(3):319-324.

10.7638/kqdlxxb-2013.0003 Sun Y，Deng X G，Wang G X，et al.A prismatic grid generation method based on constrained frame［J］.Acta Aerodynamica Sinica，2015，33(3):319-324.