基于算术平均和抽取的TDMA信号时/频差估计
2015-04-14郭付阳张子敬杨林森
郭付阳 张子敬 杨林森
(西安电子科技大学 西安 710071)
0 引言
对敌方地面辐射源的定位是电子侦察与电子对抗的任务之一。一种常用的定位技术是利用两颗卫星接收该辐射源的信号,并估计两路接收信号的时差和频差,再联合地球表面方程实现定位[1-3]。TDMA 信号为一种常用的通信信号,各通信基站通过时分多址分别和卫星进行通信,因此研究TDMA 信号的时/频差估计具有重要意义。
模糊函数是时/频差估计中常用的工具,其峰值对应两路信号的时/频差。由于TDMA 信号中各用户的时/频差不同,如果直接对主星和邻星接收信号做互模糊函数,将出现多个峰值。当用户间时/频差接近时,直接计算模糊函数无法有效区分各用户峰值,并且由于各用户间存在严重的交叉干扰,时/频差估计性能较差。针对该问题,文献[4]提出对主星信号解调分选,将各用户从主星接收信号中分离出来,再分别与邻星信号做互模糊函数,分别估计出各用户的时/频差。该方法解决了各用户间交叉干扰的问题,提高了模糊函数的相关输出信噪比,显著提升了时/频差估计性能。然而,该方法需要计算整段信号的模糊函数,当信号较长时,运算量较大,不利于实时处理。
为了实现时/频差快速估计,本文提出了基于算术平均和抽取的TDMA 信号时/频差估计方法。在模糊函数计算中,主要的运算量都来自于对混合积信号的多次FFT。由于混合积信号频谱能量主要集中在多普勒频差附近,而多普勒频差一般远小于采样频率。本文通过算术平均和抽取来降低混合积信号的长度从而减少模糊函数运算量。在理论分析的基础上,通过仿真实验验证了本方法对TDMA 信号时/频差估计的性能,并通过和已有方法的对比,显示出本方法在运算量上的优势。
1 信号模型
假设两个卫星接收到同一辐射源辐射的TDMA信号,该TDMA 信号中共有Q 个用户。由于卫星位置和运动状态的不同,邻星接收的某用户信号相对主星接收的该用户信号存在时延差和多普勒频差。双星接收的基带信号的数学模型如下所示

其中w1(t)和w2(t)为互不相关的加性噪声,sq(t)为第q 个用户,Dtq和Dfq为两路接收信号中第q 个用户的时频差,两路信号中的各用户具有不同的时频差。对于第q 个用户,有

其中L 为单个用户总通信时隙数,aql(t)和Tql分别为第l+1 次通信传输的二相码信息和通信的起始时刻,fc为载频,fql为初始相位。
2 滤波和抽取的可交换性
在信号处理的过程中,有时需要对信号抽取实现降采样,然而直接抽取往往会使信号频谱混叠,在抽取前需要对信号低通滤波,该完整的过程称为滤波抽取。
由于滤波是对整段信号处理的,而随后的抽取只选取了部分结果,大部分滤波后的数据被舍弃,因此先滤波后抽取存在巨大的计算冗余。根据文献[5],滤波和抽取存在可交换性,如图1所示。

图1 滤波和抽取的可交换性
图1 说明了先滤波后抽取的结构可以用先抽取后滤波的结构来代替,两者间的区别在于先滤波后抽取的滤波器为E(zD),而先抽取后滤波的滤波器为E(z)。虽然不是任意的一个滤波器G(z)都可以直接写成G(z)= E(zD)这样的形式,但是任意一个滤波器G(z)都可以展开,其中Ek(zD)是G(z)的多相位分量[5],因此滤波抽取的过程可以等效为图2(a)所示的滤波器结构。根据图1 给出的滤波和抽取的关系,图2(a)可以进一步用图2(b)的结构代替,从而将先低通滤波后抽取的过程等效为先抽取后滤波,抽取大大降低了数据率,提高了后续滤波过程的计算效率,实现了无冗余计算。

图2 滤波抽取的等价结构
3 TDMA 信号时/频差估计
时/频差的估计常用模糊函数来实现,模糊函数峰值对应两路信号的时/频差。信号f(t)和g(t)的模糊函数(Ambiguity function,AF)[6]定义为:

其中τ,v 分别为时延和多普勒频率,定义f(t)和g(t)的混合积信号为
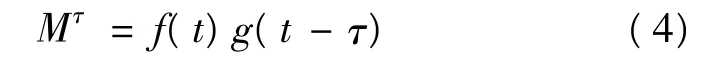
可以看出,模糊函数为混合积信号的傅立叶变换。
文献[4]对主星信号解调分选,将各用户从主星信号中分离出来,然后计算分离后的各用户与邻星信号的互模糊函数,通过二维搜索模糊函数的峰值估计各用户的时/频差。尽管该方法能够避免各用户间的干扰,降低噪声,提高了估计精度,然而,解调分选并没有减少信号的长度,文献[4]中的方法仍需要计算完整的模糊函数,运算量较大,不利于实时处理。为了提高运算速度,在文献[4]中解调分选方法的基础上,本文给出了基于算术平均和抽取的TDMA 信号时/频差估计方法。
对主星信号解调分选能够获得各用户的解析式sq(t),q=1,2,L,Q,当不考虑噪声时邻星接收到的信号相对sq(t)仅仅多了时延Δtq和多普勒频移Δfq,邻星和主星的混合积信号为

其中τ 为补偿的时延,当τ= Δtq时,有
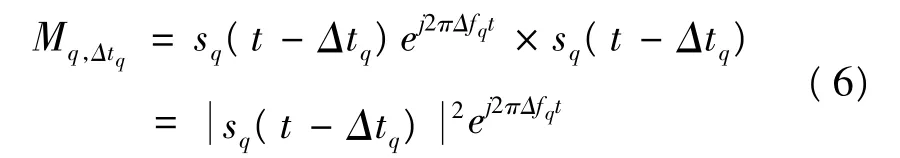
由式(6)可以看出,若两路信号间的时延差能够完全补偿,则混合积近似为一单频信号,且其频率为多普勒频差Δfq,对混合积做傅立叶变换,峰值位置对应Δfq,(Δtq,Δfq)即为模糊函数的峰值点。然而,由于时延差未知,需要搜索整个模糊函数平面,其主要运算量来源于对两路信号不同时延混合积信号的多次FFT 运算。如果能够减少混合积信号的长度,计算模糊函数的运算量将显著下降。
实际中的Δfq通常远远小于信号采样率fs,因此可用滤波抽取减少混合积信号长度。假设多普勒频差的绝对值最大为Δfmax,采样频率为fs,则理论上抽取倍数,这保证了抽取完后的频带能够覆盖到多普勒频差所有可能的取值。为了保护感兴趣的频带,低通滤波器的通带截止频率应大于Δfmax,同时为了抑制抽取带来的频谱混叠影响,滤波器频响的过渡带应尽可能短,这意味着更高的滤波器阶数,滤波需要的运算量也越多,因此在实际问题中设计滤波器时需要权衡滤波性能和运算量。
为了简化运算,我们采用最简单的算术平均滤波器G(z)= 1+z-1+…+z-(D-1),滤波器长度与抽取倍数D 相等。将G(z)代入图2(b)所示的滤波器结构,能够得到更加简化的滤波抽取结构,称之为算术平均和抽取,如图3所示。由于滤波器的权值均为1,滤波过程中不需要乘法,只需要对原混合积信号每隔D 点求和即可获得滤波抽取后的混合积信号。
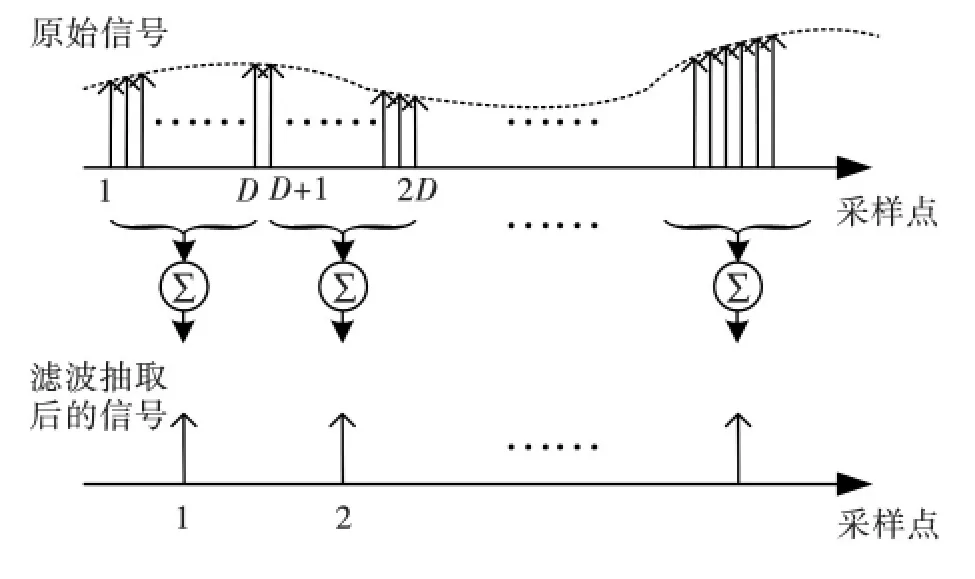
图3 算术平均和抽取过程示意图
用不同的时延补偿会得到不同的混合积信号,分别对这些混合积信号进行算术平均和抽取,再计算模糊函数,由模糊函数峰值估计时/频差。本方法具体流程如下所示:
步骤1:按式(5)对主星解调分选后得到的第q个用户sq(t)与邻星接收信号r2(t)计算混合积信号,由于不同用户以及用户与噪声均不相关,可以认为共轭相乘后的信号是第q 个用户的混合积信号Mq,τ与噪声的叠加。
步骤2:对不同时延得到的混合积信号Mq,τ分别算术平均和抽取,记处理后的混合积信号为Rq,τ。
步骤3:对不同时延对应的Rq,τ分别做傅立叶变换,由于时延完全正确补偿后的混合积信号其傅立叶变换的峰值最高,因此二维搜索所有时延对应Rq,τ的傅立叶变换的峰值,最大峰值的位置即为多普勒频差的估计Δf^q,由最大峰值对应的混合积信号可得时延差的估计Δt^q。
步骤4:对每一个解调分选后的用户信号重复如上步骤,直到估计出所有用户各自的时/频差。
4 仿真实验
假设仿真的TDMA 信号为二相编码信号,共包含5 个用户,各用户轮流进行通信,在T= 0.2s 的时间内共有25 个时隙,各用户共有5 个通信时隙,每个用户单次通信时隙不超过8ms。二相编码的数据传输速率为195.3kbps,采样率为10MHz。双星接收的TDMA 信号中5 个用户各自对应的时延差为[0μs,80μs,70μs,150μs,-150μs],多普勒频差为[0Hz,7000Hz,6000Hz,790Hz,4720Hz],其中用户2 和用户3 的时/频差相距较近。
图4 为主星信号和邻星信号在信噪比为0dB 情况下的局部互模糊函数,用户2 和用户3 由于时频差相距较近,峰值有所重叠而无法分辨,从图4 中只能观察到4 个明显峰值。
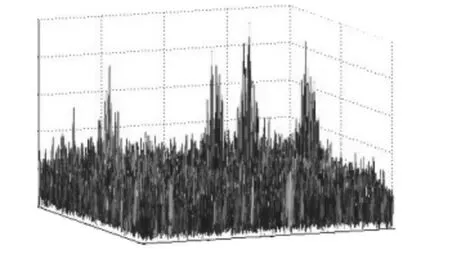
图4 双星接收信号的互模糊函数
为了体现解调分选的优势,选取解调分选得到的用户2 信号进行仿真,信噪比为0dB。图5 为主星信号解调分选得到的用户2 信号与邻星信号的局部互模糊函数,从图中可观察到模糊函数只存在单峰,这是由于解调分选将各用户成功分离的结果。对比图4 和图5 可知,直接计算模糊函数时各用户的交叉干扰十分严重,其模糊函数的噪声较高,解调分选后模糊函数的噪声显著降低。
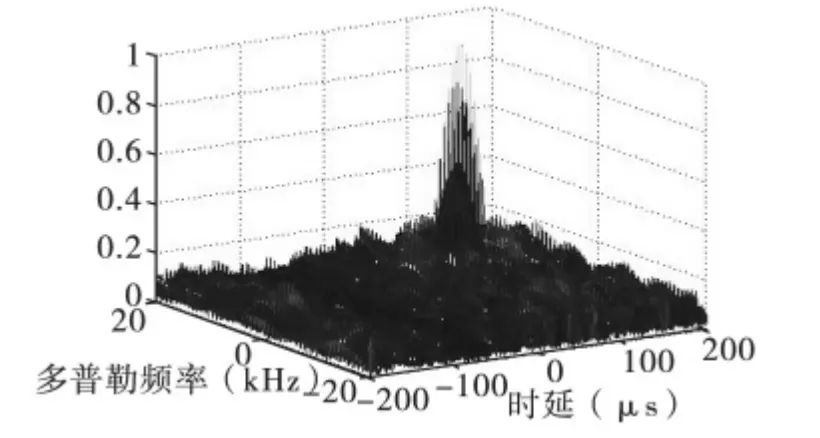
图5 解调分选的用户2 与邻星信号的互模糊函数
由前面分析可知,算术平均和抽取可以等价为图2(a)所示的先滤波后抽取结构。为了方便仿真,下面用先滤波后抽取逐步分析滤波抽取过程的频率响应。图6(a)为0dB 信噪比下解调分选得到的用户2 信号和邻星信号时延正确补偿后的混合积信号频谱与长度为20 的平均滤波器频率响应的比较。从图6(a)可以看到,时延正确补偿后的混合积近似为一单频信号,且该频率远小于采样频率。抽取倍数为20 的平均滤波器呈现出明显的低通特性,能够保留混合积信号中我们所感兴趣的频带,且能抑制不需要的高频成分。图6(b)为对混合积信号算术平均后的频谱,可以看出高频成分抑制效果明显,所感兴趣的低频成分正确保留。图6(c)为对算术平均后的混合积信号抽取后的频谱,图6(d)为解调分选得到的用户2 的混合积信号经算术平均和抽取后的局部模糊函数。对比图5(a)和图6(d)可看出,算术平均和抽取过程很好地保留了原模糊函数中所感兴趣的区域。根据图6(d)中的模糊函数峰值位置,可以得到用户2 的时频差估计为(80μs,7000Hz)。
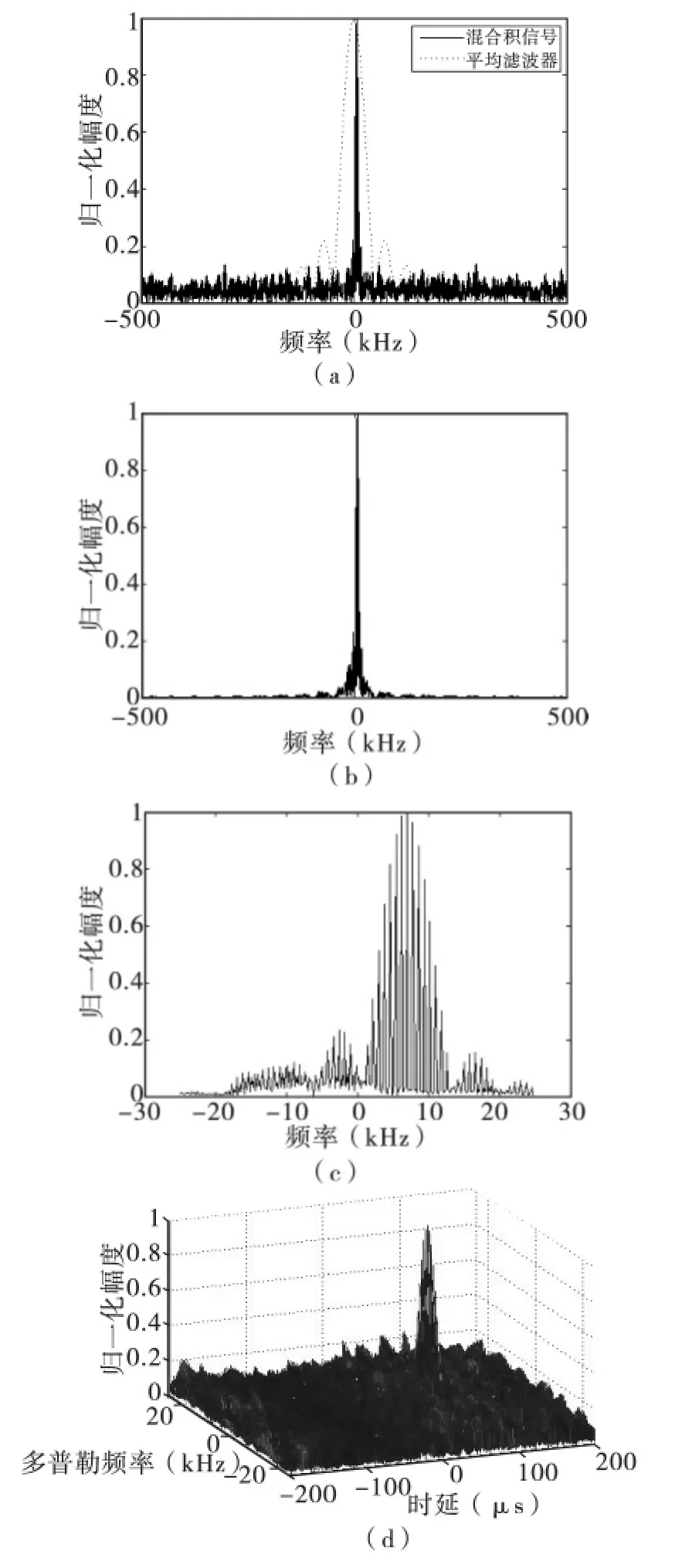
图6 算术平均和抽取过程对用户2 的混合积频谱的影响
文献[4]中提出了基于解调分选的TDMA 时/频差估计方法,本文给出的方法是在已解调分选的基础上再对混合积信号算术平均和抽取得到的。下面通过对比这两种方法的复乘次数,说明本方法在运算速度上的优势。
假设双星接收信号长度为N,抽取倍数为D,时延差可能取值个数为N。文献[4]解调分选得到的用户信号直接与邻星信号计算模糊函数,需要对不同时延补偿的长度为N 的混合积信号做傅立叶变换,运算量为N2log2N+N2。本文提出的方法通过算术平均和抽取,将混合积信号长度由N 降为N/D,由于单个时延补偿的混合积做FFT 的运算量为,则该方法计算模糊函数需要的运算量为。表1 为本方法在20 倍抽取的情况下和文献[4]的方法运算量的对比,其中信号长度N= 5000 。由表1 可以看出,抽取有效降低了计算模糊函数的运算量,在以上参数条件下本方法所需运算量仅为文献[4]中方法的10.5% 。

表1 本文方法与解调分选方法运算量对比
5 结论
针对现有TDMA 信号时/频差估计方法存在运算量较大的问题,本文提出了基于算术平均和抽取的TDMA 信号时/频差估计方法。由于模糊函数主要的运算量来自于对混合积的多次傅立叶变换,该方法通过算术平均和抽取在保留信号主要频谱的前提下有效降低混合积信号的长度,实现TDMA 信号的快速时/频差估计。仿真结果说明本文提出的方法能够快速估计TDMA 信号中各用户的时/频差,相比已有方法,运算量显著减少。
[1]Haworth D.P.,Smith N.G.,Bardelli R.Interference Localization for EUTELSAT satellites the first European transmitter location system[J].International Journal of Satellite Communications,1997,15(3):155-183.
[2]龙宁,曹广平,王勤果.双星时差频差定位系统中的多信号定位技术[J].电讯技术,2011,51(2):16-20.
[3]严航,姚山峰.基于参考站的低轨双星定位误差校正分析[J].电讯技术,2011,51(12):27-33.
[4]严航,叶尚福,朱珍珍.基于解调分选的时分多址信号时/频差参数联合估计方法[J].宇航学报,2013,34(4):531-538.
[5]VAIDYANATHAN P.P.Multirate Digital Filters,Filter Banks,Polyphase Networks,and Applications:A Tutorial[J].Proceedings of theIEEE,1990,78(1):56-93.
[6]STEIN S.Algorithms for Ambiguity function processing[J].IEEE transactions on ASSP,1981,29(3):588-599.
